北师大版八年级数学上册2.7《二次根式的乘除》一课一练(word版含答案)
文档属性
| 名称 | 北师大版八年级数学上册2.7《二次根式的乘除》一课一练(word版含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 31.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-22 15:38:12 | ||
图片预览
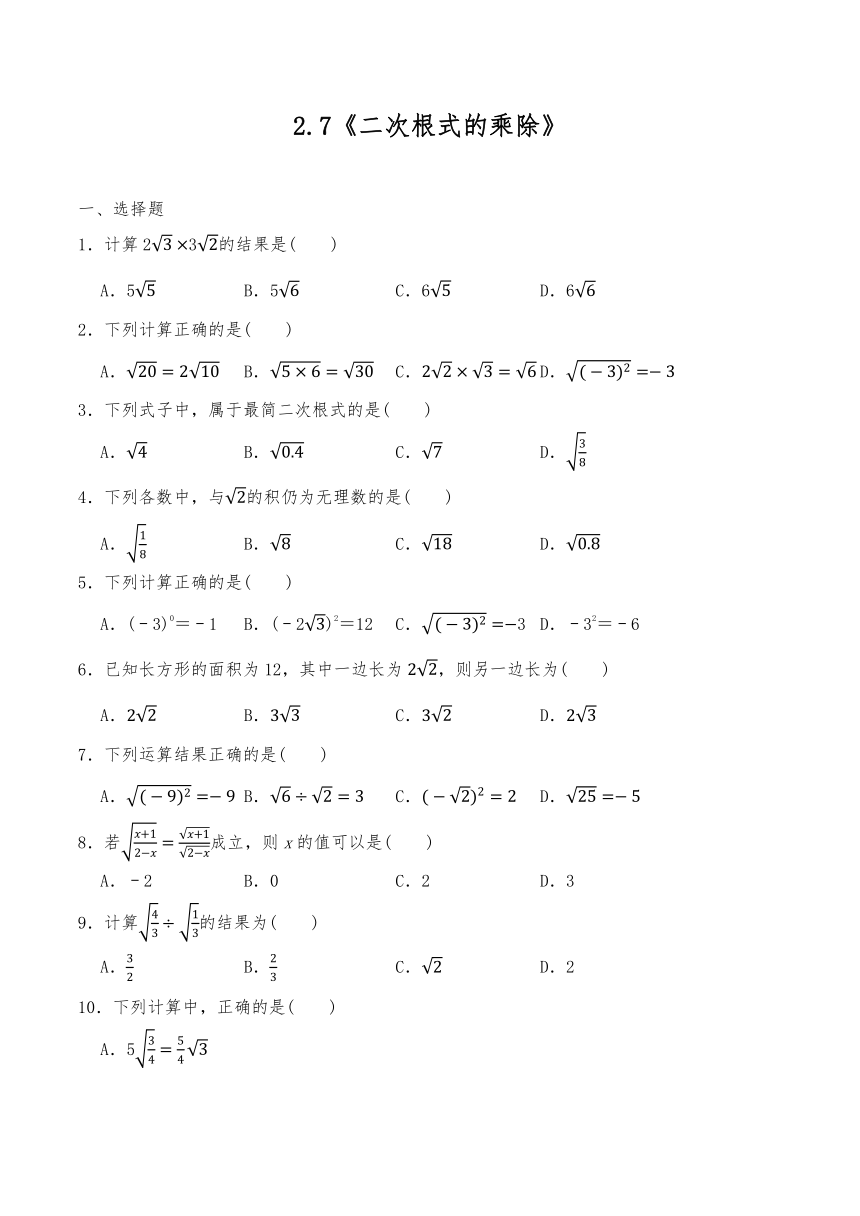


文档简介
2.7《二次根式的乘除》
一、选择题
1.计算23的结果是( )
A.5
B.5
C.6
D.6
2.下列计算正确的是( )
A.
B.
C.
D.
3.下列式子中,属于最简二次根式的是( )
A.
B.
C.
D.
4.下列各数中,与的积仍为无理数的是( )
A.
B.
C.
D.
5.下列计算正确的是( )
A.(﹣3)0=﹣1
B.(﹣2)2=12
C.3
D.﹣32=﹣6
6.已知长方形的面积为12,其中一边长为,则另一边长为( )
A.
B.
C.
D.
7.下列运算结果正确的是( )
A.
B.
C.
D.
8.若成立,则x的值可以是( )
A.﹣2
B.0
C.2
D.3
9.计算的结果为( )
A.
B.
C.
D.2
10.下列计算中,正确的是( )
A.5
B.(a>0,b>0)
C.3
D.6
二、填空题
11.把化成最简二次根式为
.
12.在根式,,,,,最简二次根式的个数有
个.
13.计算的结果是
.
14.如果一个无理数a与的积是一个有理数,写出a的一个值是
.
15.计算
.
16.计算
.
17.如果是一个整教,那么x可取的最小正整数为
,
18.化简:的结果为
.
三、解答题
19.(2019春?武汉期中)化简下列二次根式:
(1)
(2)
(3)
(4)
20.计算:
(1);
(2)4;
(3)6(﹣3);
(4)32.
21.设长方形的长与宽分别为a,b,面积为S.
①已知a=2cm,bcm,求S;
②已知Scm2,bcm,求a.
22.比较下列各组值的大小:(在横线上填“>”“<”或“=”)
4+3
;
;5+5
;…
通过观察归纳,写出能反映这种规律的一般结论,并说明你所写式子的正确性.
23.小明在学习中发现了一个“有趣”的现象:
∵,①
,②
∴.③
∴2=﹣2.④
(1)上面的推导过程中,从第
步开始出现错误(填序号);
(2)写出该步的正确结果.
24.老师在复习“二次根式”时,在黑板上写出下面的一道题作为练习:
已知a,b,用含a,b的代数式表示.小豪、小麦两位同学跑上讲台,板书了下面两种解法:
小豪:.
小麦:.
因为,.
老师看罢,提出下面的问题:
(1)两位同学的解法都正确吗?
(2)请你再给出一种不同于二人的解法?
答案
一、选择题
1.D.2.B.3.C.4.D.5.B.6.C.7.C.8.B.9.D.10.B.
二、填空题
11.3.
12.1.
13.6.
14.(答案不唯一).
15..
16..
17.6.
18.﹣1.
三、解答题
19.(1)4;
(2);
(3);
(4).
20.(1)原式4.
(2)原式=44.
(3)原式=6×(﹣3)18×4=﹣72.
(4)原式=3×230.
21.①∵a=2cm,bcm,
∴S=24(cm2);
②∵Scm2,bcm,
∴a.
22.由题意得:4﹣23=()2>0,
同理:0,
5+5)2=0,
规律为:a+b≥2.
证明:a﹣2b0.
故答案为:>,>,=.
23.(1)上面的推导过程中,从第②步开始出现错误,
故答案为:②;
(2)﹣2.
24.(1)两位同学的解法都正确.
(2)∵,
∴.
一、选择题
1.计算23的结果是( )
A.5
B.5
C.6
D.6
2.下列计算正确的是( )
A.
B.
C.
D.
3.下列式子中,属于最简二次根式的是( )
A.
B.
C.
D.
4.下列各数中,与的积仍为无理数的是( )
A.
B.
C.
D.
5.下列计算正确的是( )
A.(﹣3)0=﹣1
B.(﹣2)2=12
C.3
D.﹣32=﹣6
6.已知长方形的面积为12,其中一边长为,则另一边长为( )
A.
B.
C.
D.
7.下列运算结果正确的是( )
A.
B.
C.
D.
8.若成立,则x的值可以是( )
A.﹣2
B.0
C.2
D.3
9.计算的结果为( )
A.
B.
C.
D.2
10.下列计算中,正确的是( )
A.5
B.(a>0,b>0)
C.3
D.6
二、填空题
11.把化成最简二次根式为
.
12.在根式,,,,,最简二次根式的个数有
个.
13.计算的结果是
.
14.如果一个无理数a与的积是一个有理数,写出a的一个值是
.
15.计算
.
16.计算
.
17.如果是一个整教,那么x可取的最小正整数为
,
18.化简:的结果为
.
三、解答题
19.(2019春?武汉期中)化简下列二次根式:
(1)
(2)
(3)
(4)
20.计算:
(1);
(2)4;
(3)6(﹣3);
(4)32.
21.设长方形的长与宽分别为a,b,面积为S.
①已知a=2cm,bcm,求S;
②已知Scm2,bcm,求a.
22.比较下列各组值的大小:(在横线上填“>”“<”或“=”)
4+3
;
;5+5
;…
通过观察归纳,写出能反映这种规律的一般结论,并说明你所写式子的正确性.
23.小明在学习中发现了一个“有趣”的现象:
∵,①
,②
∴.③
∴2=﹣2.④
(1)上面的推导过程中,从第
步开始出现错误(填序号);
(2)写出该步的正确结果.
24.老师在复习“二次根式”时,在黑板上写出下面的一道题作为练习:
已知a,b,用含a,b的代数式表示.小豪、小麦两位同学跑上讲台,板书了下面两种解法:
小豪:.
小麦:.
因为,.
老师看罢,提出下面的问题:
(1)两位同学的解法都正确吗?
(2)请你再给出一种不同于二人的解法?
答案
一、选择题
1.D.2.B.3.C.4.D.5.B.6.C.7.C.8.B.9.D.10.B.
二、填空题
11.3.
12.1.
13.6.
14.(答案不唯一).
15..
16..
17.6.
18.﹣1.
三、解答题
19.(1)4;
(2);
(3);
(4).
20.(1)原式4.
(2)原式=44.
(3)原式=6×(﹣3)18×4=﹣72.
(4)原式=3×230.
21.①∵a=2cm,bcm,
∴S=24(cm2);
②∵Scm2,bcm,
∴a.
22.由题意得:4﹣23=()2>0,
同理:0,
5+5)2=0,
规律为:a+b≥2.
证明:a﹣2b0.
故答案为:>,>,=.
23.(1)上面的推导过程中,从第②步开始出现错误,
故答案为:②;
(2)﹣2.
24.(1)两位同学的解法都正确.
(2)∵,
∴.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
