2021-2022学年华东师大新版九年级上册数学《第25章 随机事件的概率》单元测试卷(word解析版)
文档属性
| 名称 | 2021-2022学年华东师大新版九年级上册数学《第25章 随机事件的概率》单元测试卷(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 152.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-22 16:06:00 | ||
图片预览




文档简介
2021-2022学年华东师大新版九年级上册数学《第25章
随机事件的概率》单元测试卷
一.选择题
1.下列事件中,必然事件是( )
A.抛出一枚硬币,落地后正面向上
B.打开电视,正在播放广告
C.篮球队员在罚球线投篮一次,未投中
D.实心铁球投入水中会沉入水底
2.下列事件是必然事件的是( )
A.打开电视机,正在播放篮球比赛
B.守株待兔
C.明天是晴天
D.在只装有5个红球的袋中摸出1球,是红球
3.小伟掷一个质地均匀的正方体骰子,骰子的六个面上分别刻有1到6的点数.下列事件是必然事件的是( )
A.掷一次骰子,朝上的一面的点数大于0
B.掷一次骰子,朝上的一面的点数为7
C.掷一次骰子,朝上的一面的点数为4
D.掷两次骰子,朝上的一面的点数都是3
4.在作图钉落地的实验中,正确的是( )
A.甲做了4000次,得出针尖触地的机会约为46%,于是他断定在做第4001次时,针尖肯定不会触地
B.乙认为一次一次做,速度太慢,他拿来了大把材料、形状及大小都完全一样的图钉,随意朝上轻轻抛出,然后统计针尖触地的次数,这样大大提高了速度
C.老师安排每位同学回家做实验,图钉自由选取
D.老师安排同学回家做实验,图钉统一发(完全一样的图钉).同学交来的结果,老师挑选他满意的进行统计,他不满意的就不要
5.柜子里有5双鞋,取出一只鞋是右脚鞋的概率是( )
A.
B.
C.
D.
6.下列说法中,正确的是( )
A.“任意画一个多边形,其内角和是360°”是必然事件
B.“如果a2=b2,那么a=b”是必然事件
C.可能性是50%的事件,是指在两次试验中一定有一次会发生
D.“从一副扑克牌(含大小王)中抽一张,恰好是红桃”是随机事件
7.下列说法正确的是( )
A.投掷一枚质地均匀的硬币1000次,正面朝上的次数一定是500次
B.天气预报“明天降水概率10%”,是指明天有10%的时间会下雨
C.一种福利彩票中奖率是千分之一,则买这种彩票1000张,一定会中奖
D.连续掷一枚均匀硬币,若5次都是正面朝上,则第六次仍然可能正面朝上
8.下列事件为必然事件的是( )
A.打开电视机,它正在播广告
B.投掷一枚普通的正方体骰子,掷得的点数小于7
C.某彩票的中奖机会是1%,买1张一定不会中奖
D.抛掷一枚硬币,一定正面朝上
9.在一个不透明的袋子里装有红球、黄球共20个,这些球除颜色外都相同.小明通过多次试验发现,摸出红球的频率稳定在0.25左右,则袋子中红球的个数最有可能是( )
A.5
B.10
C.12
D.15
10.口袋中有14个红球和若干个白球,这些球除颜色外都相同,从口袋中随机摸出一个球,记下颜色后放回,多次实验后发现摸到白球的频率稳定在0.3,则白球的个数是( )
A.5
B.6
C.7
D.8
二.填空题
11.在一个不透明的布袋中装有红色、白色玻璃球共40个,除颜色外其他完全相同.小明通过多次摸球试验后发现,其中摸到红色球的频率稳定在15%左右,则口袋中红色球可能有
个.
12.某校学生小明每天骑自行车上学时都要经过一个十字路口,该十字路口有红、黄、绿三色交通信号灯,他在路口遇到红灯的概率为,遇到黄灯的概率为,那么他遇到绿灯的概率为
.
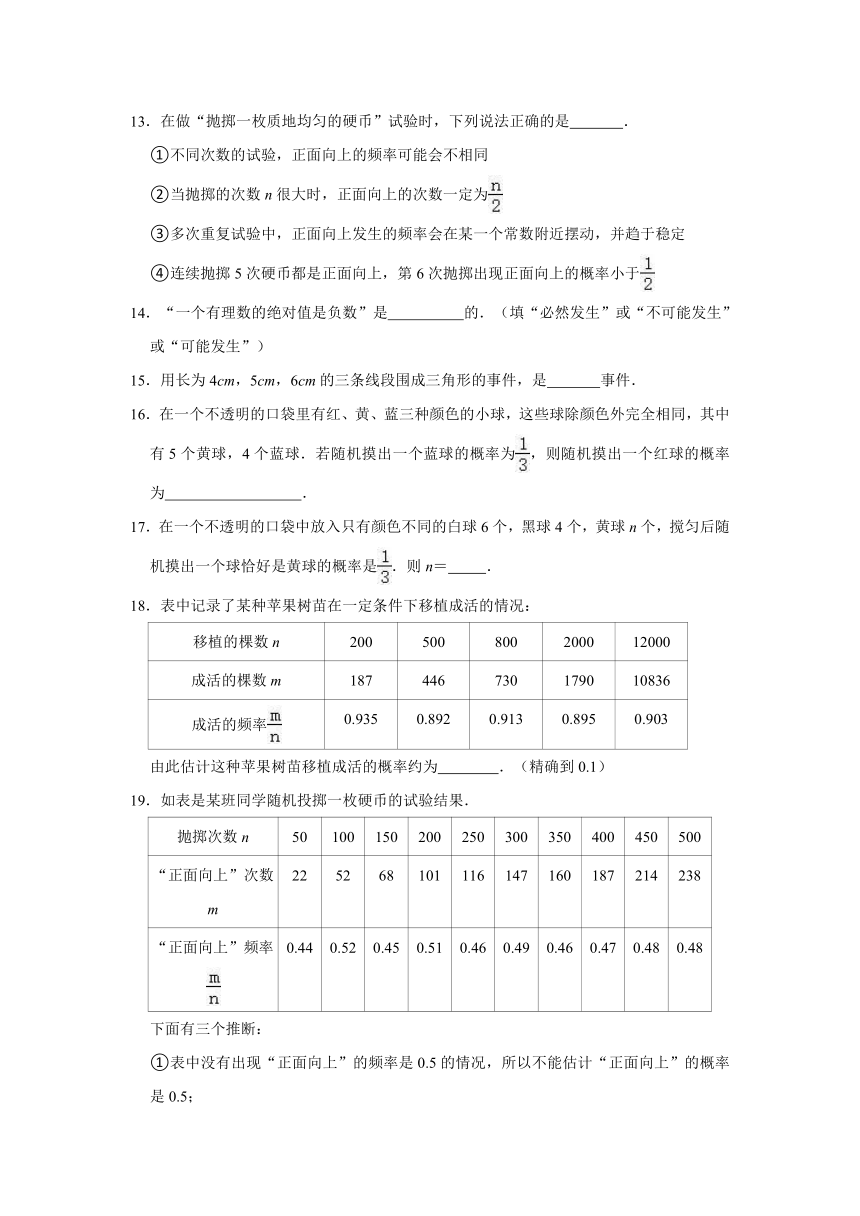
13.在做“抛掷一枚质地均匀的硬币”试验时,下列说法正确的是
.
①不同次数的试验,正面向上的频率可能会不相同
②当抛掷的次数n很大时,正面向上的次数一定为
③多次重复试验中,正面向上发生的频率会在某一个常数附近摆动,并趋于稳定
④连续抛掷5次硬币都是正面向上,第6次抛掷出现正面向上的概率小于
14.“一个有理数的绝对值是负数”是
的.(填“必然发生”或“不可能发生”或“可能发生”)
15.用长为4cm,5cm,6cm的三条线段围成三角形的事件,是
事件.
16.在一个不透明的口袋里有红、黄、蓝三种颜色的小球,这些球除颜色外完全相同,其中有5个黄球,4个蓝球.若随机摸出一个蓝球的概率为,则随机摸出一个红球的概率为
.
17.在一个不透明的口袋中放入只有颜色不同的白球6个,黑球4个,黄球n个,搅匀后随机摸出一个球恰好是黄球的概率是.则n=
.
18.表中记录了某种苹果树苗在一定条件下移植成活的情况:
移植的棵数n
200
500
800
2000
12000
成活的棵数m
187
446
730
1790
10836
成活的频率
0.935
0.892
0.913
0.895
0.903
由此估计这种苹果树苗移植成活的概率约为
.(精确到0.1)
19.如表是某班同学随机投掷一枚硬币的试验结果.
抛掷次数n
50
100
150
200
250
300
350
400
450
500
“正面向上”次数m
22
52
68
101
116
147
160
187
214
238
“正面向上”频率
0.44
0.52
0.45
0.51
0.46
0.49
0.46
0.47
0.48
0.48
下面有三个推断:
①表中没有出现“正面向上”的频率是0.5的情况,所以不能估计“正面向上”的概率是0.5;
②这些次试验投掷次数的最大值是500,此时“正面向上”的频率是0.48,所以“正面向上”的概率是0.48;
③投掷硬币“正面向上”的概率应该是确定的,但是大量重复试验反映的规律并非在每一次试验中都发生;
其中合理的是
(填写序号).
20.“抛掷一枚质地均匀的硬币,正面向上”是
事件(从“必然”、“随机”、“不可能”中选一个).
三.解答题
21.在一个不透明的口袋中装着大小、外形等一模一样的5个红球、3个蓝球和2个白球,它们已经在口袋中被搅匀了.请判断以下事件是不确定事件、不可能事件,还是必然事件.
(1)从口袋中任意取出一个球,是一个白球;
(2)从口袋中一次任取5个球,全是蓝球;
(3)从口袋中一次任意取出9个球,恰好红蓝白三种颜色的球都齐了.
22.在一个不透明的口袋里,装有6个除颜色外其余都相同的小球,其中2个红球,2个白球,2个黑球.它们已在口袋中被搅匀,现在有一个事件:从口袋中任意摸出n个球,红球、白球、黑球至少各有一个.
(1)当n为何值时,这个事件必然发生?
(2)当n为何值时,这个事件不可能发生?
(3)当n为何值时,这个事件可能发生?
23.一枚普通的正方体骰子,每个面上分别标有1,2,3,4,5,6,在抛掷一枚普通的正方体骰子的过程中,请用语言描述:
(1)一件不可能事件:
(2)一件必然事件:
(3)一件不确定事件:
.
24.如图,一个均匀的转盘被平均分成10等份,分别标有1,2,3,4,5,6,7,8,9,10这10个数字.转动转盘,当转盘停止后,指针指向的数字即为转出的数字.
两人参与游戏:一人转动转盘,另一人猜数,若所猜数字与转出的数字相符,则猜数的人获胜,否则转动转盘的人获胜.猜数的规则从下面三种中选一种:
(1)猜“是奇数”或“是偶数”;
(2)猜“是3的倍数”或“不是3的倍数”;
(3)猜“是大于6的数”或“不是大于6的数”.
如果轮到你猜数,那么为了尽可能获胜,你将选择哪一种猜数方法?怎样猜?请说明理由!
25.在“六?一”儿童节来临之际,某妇女儿童用品商场为吸引顾客,设立了一个可以自由转动的转盘(如图,转盘被平均分成20份),并规定:顾客每购物满100元,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得80元、50元、20元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可直接获得15元的购物券.转转盘和直接获得购物券,你认为哪种方式对顾客更合算?请说明理由.
26.在一次促销活动中,某商场为了吸引顾客,设立了一个可以自由转动的转盘(如图,转盘被平均分成16份),并规定:顾客每购买100元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得50元、30元、20元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券10元.
(1)求每转动一次转盘所获购物券金额的平均数;
(2)如果你在该商场消费125元,你会选择转转盘还是直接获得购物券?说明理由.
27.某厂为新型号电视机上市举办促销活动,顾客每买一台该型号电视机,可获得一次抽奖机会,该厂拟按10%设大奖,其余90%为小奖.
厂家设计的抽奖方案是:在一个不透明的盒子中,放入10个黄球和90个白球,这些球除颜色外都相同,搅匀后从中任意摸出1个球,摸到黄球的顾客获得大奖,摸到白球的顾客获得小奖.
(1)厂家请教了一位数学老师,他设计的抽奖方案是:在一个不透明的盒子中,放入2个黄球和3个白球,这些球除颜色外都相同,搅匀后从中任意摸出2个球,摸到的2个球都是黄球的顾客获得大奖,其余的顾客获得小奖.该抽奖方案符合厂家的设奖要求吗?请说明理由;
(2)下图是一个可以自由转动的转盘,请你将转盘分为2个扇形区域,分别涂上黄、白两种颜色,并设计抽奖方案,使其符合厂家的设奖要求.(友情提醒:1.转盘上用文字注明颜色和扇形的圆心角的度数,2、结合转盘简述获奖方式,不需说明理由.)
参考答案与试题解析
一.选择题
1.解:抛出一枚硬币,落地后正面向上是随机事件,A不正确;
打开电视,正在播放广告是随机事件,B不正确;
篮球队员在罚球线投篮一次,未投中是随机事件,C不正确;
实心铁球投入水中会沉入水底是必然事件,D正确.
故选:D.
2.解:打开电视机,正在播放篮球比赛是随机事件,A不正确;
守株待兔是随机事件,B不正确;
明天是晴天是随机事件,C不正确;
在只装有5个红球的袋中摸出1球,是红球是必然事件;
故选:D.
3.解:A、一个质地均匀的正方体骰子,骰子的六个面上分别刻有1到6的点数,故掷一次骰子,朝上的一面的点数大于0是必然事件,故本选项正确;
B、掷一次骰子,朝上的一面的点数为7是随机事件,故本选项错误;
C、掷一次骰子,朝上的一面的点数为4是随机事件,故本选项错误;
D、掷两次骰子,朝上的一面的点数都是3是随机事件,故本选项错误.
故选:A.
4.解:A、在做第4001次时,针尖可能触地,也可能不触地,故错误,不符合题意;
B、符合模拟实验的条件,正确,符合题意;
C、应选择相同的图钉,在类似的条件下实验,故错误,不符合题意;
D、所有的实验结果都是有可能发生,也有可能不发生的,故错误,不符合题意;
故选:B.
5.解:5双鞋就是10只,其中右脚的有5只,所以取出一只鞋是右脚鞋的概率是=.
故选:A.
6.解:A.“任意画一个多边形,其内角和是360°”是随机事件,故原说法错误;
B.“当a、b是不为零的相反数时,如果a2=b2,那么a≠b”,故原说法错误;
C.可能性是50%的事件,是指在多次试验中一定有一次会发生,故原说法错误;
D.“从一副扑克牌(含大小王)中抽一张,恰好是红桃”是随机事件,说法正确.
故选:D.
7.解:A、投掷一枚质地均匀的硬币1000次,正面朝上的次数不一定是500次,故原说法错误,不合题意;
B、天气预报“明天降水概率10%”,是指明天下雨的可能性是10%,故原说法错误,不合题意;
C、一种福利彩票中奖率是千分之一,但买这种彩票1000张,也不一定会中奖,故原说法错误,不合题意;
D、连续掷一枚均匀硬币,若5次都是正面朝上,则第六次仍然可能正面朝上,正确.
故选:D.
8.解:A.打开电视机,它正在播广告,属于随机事件;
B.投掷一枚普通的正方体骰子,掷得的点数小于7,属于必然事件;
C.某彩票的中奖机会是1%,买1张不会中奖,属于随机事件;
D.抛掷一枚硬币,正面朝上,属于随机事件;
故选:B.
9.解:设袋子中红球有x个,
根据题意,得:=0.25,
解得x=5,
∴袋子中红球的个数最有可能是5个,
故选:A.
10.解:设袋中白球有x个,根据题意得:=0.3,
解得:x=6,
经检验:x=6是分式方程的解,
故选:B.
二.填空题
11.解:红球个数为:40×15%=6个.
故答案为:6.
12.解:∵经过一个十字路口,共有红、黄、绿三色交通信号灯,
∴在路口遇到红灯、黄灯、绿灯的概率之和是1,
∵在路口遇到红灯的概率为,遇到黄灯的概率为,
∴遇到绿灯的概率为1﹣=;
故答案为:.
13.解:①不同次数的试验,正面向上的频率可能会不相同,故本选项正确;
②当抛掷的次数n很大时,正面向上的次数更接近;故本选项错误;
③多次重复试验中,正面向上发生的频率会在某一个常数附近摆动,并趋于稳定;故故本选项正确;
④连续抛掷5次硬币都是正面向上,第6次抛掷出现正面向上的概率可能是,故本选项错误.
故答案为:①③.
14.解:一个有理数的绝对值是负数”是不可能发生的.
故答案是:不可能发生.
15.解:根据三角形三边关系可知:4cm,5cm,6cm的三条线段一定能围成三角形,所以是必然事件.
16.解:∵在一个不透明的口袋里有红、黄、蓝三种颜色的小球,三种球除颜色外其他完全相同,其中有5个黄球,4个蓝球,
随机摸出一个蓝球的概率是,
设红球有x个,
∴=,
解得:x=3
∴随机摸出一个红球的概率是:=.
故答案为:.
17.解:∵口袋中装有白球6个,黑球4个,黄球n个,∴球的总个数为6+4+n,
∵从中随机摸出一个球,摸到黄球的概率为,
∴=,
解得,n=5.
故答案为5.
18.解:根据表格数据可知:
苹果树苗移植成活的频率近似值为0.9,
所以估计这种苹果树苗移植成活的概率约为0.9.
故答案为:0.9.
19.解:①随着试验次数的增加,“正面向上”的频率总在0.5附近摆动,显示出一定的稳定性,可以估计“正面向上”的概率是0.5,故错误;
②这些次试验投掷次数的最大值是500,此时“正面向上”的频率是0.48,所以“正面向上”的概率是0.48,错误;
③投掷硬币“正面向上”的概率应该是确定的,但是大量重复试验反映的规律并非在每一次试验中都发生,正确;
故答案为:③.
20.解:“抛掷一枚质地均匀的硬币,正面向上”是
随机事件,
故答案为:随机.
三.解答题
21.解:(1)从口袋中任意取出一个球,可能是一个白球、一个红球也可能是一个蓝球,
∴从口袋中任意取出一个球,是一个白球是随机事件,即不确定事件;
(2)口袋中只有3个蓝球,
∴从口袋中一次任取5个球,全是蓝球是不可能事件;
(3)从口袋中一次任意取出9个球,恰好红蓝白三种颜色的球都齐了是必然事件.
22.解:(1)当n=5或6时,这个事件必然发生;
(2)当n=1或2时,这个事件不可能发生;
(3)当n=3或4时,这个事件为可能发生.
23.解:答案不唯一
(1)如出现数字7朝上;(1分)
(2)如出现朝上的点数小于7;(1分)
(3)如出现朝上的点数为5.(1分)
24.解:(1)共有10种等可能出现的结果数,其中“是奇数”的有5种,“是偶数”的也有5种,因此“是奇数”“是偶数”的可能性都是50%,
(2)共有10种等可能出现的结果数,其中“是3的倍数”的有3种,“不是3的倍数”的7种,因此“是3的倍数”可能性是30%,“不是3的倍数”的可能性是70%,
(3)共有10种等可能出现的结果数,其中“是大于6的数”的有4种,“不是大于6的数”的有6种,因此“是大于6的数”可能性是40%,“不是大于6的数”的可能性是60%,
因此,猜数者选择“不是3的倍数”,这样获胜的可能性为70%,获胜的可能性最大.
25.解:因为转转盘所获得的购物券为:80×+50×+20×=16.5(元),(4分)
∵16.5元>15元
∴选择转转盘对顾客更合算.
26.解:(1)50×+30×+20×=11.875(元);
(2)虽然转动一次转盘,平均可以获得11.875元,但是获取的概率毕竟只有十六之七,领取10元购物券的机会却是百分之一百,虽然收益低,却更稳妥一些,因此说,这两种选择应该都是可以的.
27.解:(1)该抽奖方案符合厂家的设奖要求:
分别用黄1、黄2、白1、白2、白3表示这5个球,从中任意摸出2个球,可能出现的结果有:
(黄1,黄2)、(黄1,白1)、(黄1,白2)、(黄1,白3)、
(黄2,黄1)、(黄2,白1)、(黄2,白2)、(黄2,白3)、
(白1,黄1)、(白1,黄2)、(白1.白2)、(白1,白3)、
(白2,黄1)、(白2,黄2)、(白2,白1)、(白2,白3)、
(白3,黄1)、(白3,黄2)、(白3,白1)、(白3,白2)
共有20种,它们出现的可能性相同.
所有的结果中,满足摸到的2个球都是黄球(记为事件A)的结果有2种,即(黄1,黄2)或(黄2,黄1),
所以P(两黄球)==,即顾客获得大奖的概率为10%,获得小奖的概率为90%;
(2)本题答案不唯一,下列解法供参考.
如图,将转盘中圆心角为36°的扇形区域涂上黄色,其余的区域涂上白色,顾客每购买一台该型号电视机,可获得一次转动转盘的机会,任意转动这个转盘,当转盘停止时,指针指向黄色区域获得大奖,指向白色区域获得小奖.
随机事件的概率》单元测试卷
一.选择题
1.下列事件中,必然事件是( )
A.抛出一枚硬币,落地后正面向上
B.打开电视,正在播放广告
C.篮球队员在罚球线投篮一次,未投中
D.实心铁球投入水中会沉入水底
2.下列事件是必然事件的是( )
A.打开电视机,正在播放篮球比赛
B.守株待兔
C.明天是晴天
D.在只装有5个红球的袋中摸出1球,是红球
3.小伟掷一个质地均匀的正方体骰子,骰子的六个面上分别刻有1到6的点数.下列事件是必然事件的是( )
A.掷一次骰子,朝上的一面的点数大于0
B.掷一次骰子,朝上的一面的点数为7
C.掷一次骰子,朝上的一面的点数为4
D.掷两次骰子,朝上的一面的点数都是3
4.在作图钉落地的实验中,正确的是( )
A.甲做了4000次,得出针尖触地的机会约为46%,于是他断定在做第4001次时,针尖肯定不会触地
B.乙认为一次一次做,速度太慢,他拿来了大把材料、形状及大小都完全一样的图钉,随意朝上轻轻抛出,然后统计针尖触地的次数,这样大大提高了速度
C.老师安排每位同学回家做实验,图钉自由选取
D.老师安排同学回家做实验,图钉统一发(完全一样的图钉).同学交来的结果,老师挑选他满意的进行统计,他不满意的就不要
5.柜子里有5双鞋,取出一只鞋是右脚鞋的概率是( )
A.
B.
C.
D.
6.下列说法中,正确的是( )
A.“任意画一个多边形,其内角和是360°”是必然事件
B.“如果a2=b2,那么a=b”是必然事件
C.可能性是50%的事件,是指在两次试验中一定有一次会发生
D.“从一副扑克牌(含大小王)中抽一张,恰好是红桃”是随机事件
7.下列说法正确的是( )
A.投掷一枚质地均匀的硬币1000次,正面朝上的次数一定是500次
B.天气预报“明天降水概率10%”,是指明天有10%的时间会下雨
C.一种福利彩票中奖率是千分之一,则买这种彩票1000张,一定会中奖
D.连续掷一枚均匀硬币,若5次都是正面朝上,则第六次仍然可能正面朝上
8.下列事件为必然事件的是( )
A.打开电视机,它正在播广告
B.投掷一枚普通的正方体骰子,掷得的点数小于7
C.某彩票的中奖机会是1%,买1张一定不会中奖
D.抛掷一枚硬币,一定正面朝上
9.在一个不透明的袋子里装有红球、黄球共20个,这些球除颜色外都相同.小明通过多次试验发现,摸出红球的频率稳定在0.25左右,则袋子中红球的个数最有可能是( )
A.5
B.10
C.12
D.15
10.口袋中有14个红球和若干个白球,这些球除颜色外都相同,从口袋中随机摸出一个球,记下颜色后放回,多次实验后发现摸到白球的频率稳定在0.3,则白球的个数是( )
A.5
B.6
C.7
D.8
二.填空题
11.在一个不透明的布袋中装有红色、白色玻璃球共40个,除颜色外其他完全相同.小明通过多次摸球试验后发现,其中摸到红色球的频率稳定在15%左右,则口袋中红色球可能有
个.
12.某校学生小明每天骑自行车上学时都要经过一个十字路口,该十字路口有红、黄、绿三色交通信号灯,他在路口遇到红灯的概率为,遇到黄灯的概率为,那么他遇到绿灯的概率为
.
13.在做“抛掷一枚质地均匀的硬币”试验时,下列说法正确的是
.
①不同次数的试验,正面向上的频率可能会不相同
②当抛掷的次数n很大时,正面向上的次数一定为
③多次重复试验中,正面向上发生的频率会在某一个常数附近摆动,并趋于稳定
④连续抛掷5次硬币都是正面向上,第6次抛掷出现正面向上的概率小于
14.“一个有理数的绝对值是负数”是
的.(填“必然发生”或“不可能发生”或“可能发生”)
15.用长为4cm,5cm,6cm的三条线段围成三角形的事件,是
事件.
16.在一个不透明的口袋里有红、黄、蓝三种颜色的小球,这些球除颜色外完全相同,其中有5个黄球,4个蓝球.若随机摸出一个蓝球的概率为,则随机摸出一个红球的概率为
.
17.在一个不透明的口袋中放入只有颜色不同的白球6个,黑球4个,黄球n个,搅匀后随机摸出一个球恰好是黄球的概率是.则n=
.
18.表中记录了某种苹果树苗在一定条件下移植成活的情况:
移植的棵数n
200
500
800
2000
12000
成活的棵数m
187
446
730
1790
10836
成活的频率
0.935
0.892
0.913
0.895
0.903
由此估计这种苹果树苗移植成活的概率约为
.(精确到0.1)
19.如表是某班同学随机投掷一枚硬币的试验结果.
抛掷次数n
50
100
150
200
250
300
350
400
450
500
“正面向上”次数m
22
52
68
101
116
147
160
187
214
238
“正面向上”频率
0.44
0.52
0.45
0.51
0.46
0.49
0.46
0.47
0.48
0.48
下面有三个推断:
①表中没有出现“正面向上”的频率是0.5的情况,所以不能估计“正面向上”的概率是0.5;
②这些次试验投掷次数的最大值是500,此时“正面向上”的频率是0.48,所以“正面向上”的概率是0.48;
③投掷硬币“正面向上”的概率应该是确定的,但是大量重复试验反映的规律并非在每一次试验中都发生;
其中合理的是
(填写序号).
20.“抛掷一枚质地均匀的硬币,正面向上”是
事件(从“必然”、“随机”、“不可能”中选一个).
三.解答题
21.在一个不透明的口袋中装着大小、外形等一模一样的5个红球、3个蓝球和2个白球,它们已经在口袋中被搅匀了.请判断以下事件是不确定事件、不可能事件,还是必然事件.
(1)从口袋中任意取出一个球,是一个白球;
(2)从口袋中一次任取5个球,全是蓝球;
(3)从口袋中一次任意取出9个球,恰好红蓝白三种颜色的球都齐了.
22.在一个不透明的口袋里,装有6个除颜色外其余都相同的小球,其中2个红球,2个白球,2个黑球.它们已在口袋中被搅匀,现在有一个事件:从口袋中任意摸出n个球,红球、白球、黑球至少各有一个.
(1)当n为何值时,这个事件必然发生?
(2)当n为何值时,这个事件不可能发生?
(3)当n为何值时,这个事件可能发生?
23.一枚普通的正方体骰子,每个面上分别标有1,2,3,4,5,6,在抛掷一枚普通的正方体骰子的过程中,请用语言描述:
(1)一件不可能事件:
(2)一件必然事件:
(3)一件不确定事件:
.
24.如图,一个均匀的转盘被平均分成10等份,分别标有1,2,3,4,5,6,7,8,9,10这10个数字.转动转盘,当转盘停止后,指针指向的数字即为转出的数字.
两人参与游戏:一人转动转盘,另一人猜数,若所猜数字与转出的数字相符,则猜数的人获胜,否则转动转盘的人获胜.猜数的规则从下面三种中选一种:
(1)猜“是奇数”或“是偶数”;
(2)猜“是3的倍数”或“不是3的倍数”;
(3)猜“是大于6的数”或“不是大于6的数”.
如果轮到你猜数,那么为了尽可能获胜,你将选择哪一种猜数方法?怎样猜?请说明理由!
25.在“六?一”儿童节来临之际,某妇女儿童用品商场为吸引顾客,设立了一个可以自由转动的转盘(如图,转盘被平均分成20份),并规定:顾客每购物满100元,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得80元、50元、20元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可直接获得15元的购物券.转转盘和直接获得购物券,你认为哪种方式对顾客更合算?请说明理由.
26.在一次促销活动中,某商场为了吸引顾客,设立了一个可以自由转动的转盘(如图,转盘被平均分成16份),并规定:顾客每购买100元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得50元、30元、20元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券10元.
(1)求每转动一次转盘所获购物券金额的平均数;
(2)如果你在该商场消费125元,你会选择转转盘还是直接获得购物券?说明理由.
27.某厂为新型号电视机上市举办促销活动,顾客每买一台该型号电视机,可获得一次抽奖机会,该厂拟按10%设大奖,其余90%为小奖.
厂家设计的抽奖方案是:在一个不透明的盒子中,放入10个黄球和90个白球,这些球除颜色外都相同,搅匀后从中任意摸出1个球,摸到黄球的顾客获得大奖,摸到白球的顾客获得小奖.
(1)厂家请教了一位数学老师,他设计的抽奖方案是:在一个不透明的盒子中,放入2个黄球和3个白球,这些球除颜色外都相同,搅匀后从中任意摸出2个球,摸到的2个球都是黄球的顾客获得大奖,其余的顾客获得小奖.该抽奖方案符合厂家的设奖要求吗?请说明理由;
(2)下图是一个可以自由转动的转盘,请你将转盘分为2个扇形区域,分别涂上黄、白两种颜色,并设计抽奖方案,使其符合厂家的设奖要求.(友情提醒:1.转盘上用文字注明颜色和扇形的圆心角的度数,2、结合转盘简述获奖方式,不需说明理由.)
参考答案与试题解析
一.选择题
1.解:抛出一枚硬币,落地后正面向上是随机事件,A不正确;
打开电视,正在播放广告是随机事件,B不正确;
篮球队员在罚球线投篮一次,未投中是随机事件,C不正确;
实心铁球投入水中会沉入水底是必然事件,D正确.
故选:D.
2.解:打开电视机,正在播放篮球比赛是随机事件,A不正确;
守株待兔是随机事件,B不正确;
明天是晴天是随机事件,C不正确;
在只装有5个红球的袋中摸出1球,是红球是必然事件;
故选:D.
3.解:A、一个质地均匀的正方体骰子,骰子的六个面上分别刻有1到6的点数,故掷一次骰子,朝上的一面的点数大于0是必然事件,故本选项正确;
B、掷一次骰子,朝上的一面的点数为7是随机事件,故本选项错误;
C、掷一次骰子,朝上的一面的点数为4是随机事件,故本选项错误;
D、掷两次骰子,朝上的一面的点数都是3是随机事件,故本选项错误.
故选:A.
4.解:A、在做第4001次时,针尖可能触地,也可能不触地,故错误,不符合题意;
B、符合模拟实验的条件,正确,符合题意;
C、应选择相同的图钉,在类似的条件下实验,故错误,不符合题意;
D、所有的实验结果都是有可能发生,也有可能不发生的,故错误,不符合题意;
故选:B.
5.解:5双鞋就是10只,其中右脚的有5只,所以取出一只鞋是右脚鞋的概率是=.
故选:A.
6.解:A.“任意画一个多边形,其内角和是360°”是随机事件,故原说法错误;
B.“当a、b是不为零的相反数时,如果a2=b2,那么a≠b”,故原说法错误;
C.可能性是50%的事件,是指在多次试验中一定有一次会发生,故原说法错误;
D.“从一副扑克牌(含大小王)中抽一张,恰好是红桃”是随机事件,说法正确.
故选:D.
7.解:A、投掷一枚质地均匀的硬币1000次,正面朝上的次数不一定是500次,故原说法错误,不合题意;
B、天气预报“明天降水概率10%”,是指明天下雨的可能性是10%,故原说法错误,不合题意;
C、一种福利彩票中奖率是千分之一,但买这种彩票1000张,也不一定会中奖,故原说法错误,不合题意;
D、连续掷一枚均匀硬币,若5次都是正面朝上,则第六次仍然可能正面朝上,正确.
故选:D.
8.解:A.打开电视机,它正在播广告,属于随机事件;
B.投掷一枚普通的正方体骰子,掷得的点数小于7,属于必然事件;
C.某彩票的中奖机会是1%,买1张不会中奖,属于随机事件;
D.抛掷一枚硬币,正面朝上,属于随机事件;
故选:B.
9.解:设袋子中红球有x个,
根据题意,得:=0.25,
解得x=5,
∴袋子中红球的个数最有可能是5个,
故选:A.
10.解:设袋中白球有x个,根据题意得:=0.3,
解得:x=6,
经检验:x=6是分式方程的解,
故选:B.
二.填空题
11.解:红球个数为:40×15%=6个.
故答案为:6.
12.解:∵经过一个十字路口,共有红、黄、绿三色交通信号灯,
∴在路口遇到红灯、黄灯、绿灯的概率之和是1,
∵在路口遇到红灯的概率为,遇到黄灯的概率为,
∴遇到绿灯的概率为1﹣=;
故答案为:.
13.解:①不同次数的试验,正面向上的频率可能会不相同,故本选项正确;
②当抛掷的次数n很大时,正面向上的次数更接近;故本选项错误;
③多次重复试验中,正面向上发生的频率会在某一个常数附近摆动,并趋于稳定;故故本选项正确;
④连续抛掷5次硬币都是正面向上,第6次抛掷出现正面向上的概率可能是,故本选项错误.
故答案为:①③.
14.解:一个有理数的绝对值是负数”是不可能发生的.
故答案是:不可能发生.
15.解:根据三角形三边关系可知:4cm,5cm,6cm的三条线段一定能围成三角形,所以是必然事件.
16.解:∵在一个不透明的口袋里有红、黄、蓝三种颜色的小球,三种球除颜色外其他完全相同,其中有5个黄球,4个蓝球,
随机摸出一个蓝球的概率是,
设红球有x个,
∴=,
解得:x=3
∴随机摸出一个红球的概率是:=.
故答案为:.
17.解:∵口袋中装有白球6个,黑球4个,黄球n个,∴球的总个数为6+4+n,
∵从中随机摸出一个球,摸到黄球的概率为,
∴=,
解得,n=5.
故答案为5.
18.解:根据表格数据可知:
苹果树苗移植成活的频率近似值为0.9,
所以估计这种苹果树苗移植成活的概率约为0.9.
故答案为:0.9.
19.解:①随着试验次数的增加,“正面向上”的频率总在0.5附近摆动,显示出一定的稳定性,可以估计“正面向上”的概率是0.5,故错误;
②这些次试验投掷次数的最大值是500,此时“正面向上”的频率是0.48,所以“正面向上”的概率是0.48,错误;
③投掷硬币“正面向上”的概率应该是确定的,但是大量重复试验反映的规律并非在每一次试验中都发生,正确;
故答案为:③.
20.解:“抛掷一枚质地均匀的硬币,正面向上”是
随机事件,
故答案为:随机.
三.解答题
21.解:(1)从口袋中任意取出一个球,可能是一个白球、一个红球也可能是一个蓝球,
∴从口袋中任意取出一个球,是一个白球是随机事件,即不确定事件;
(2)口袋中只有3个蓝球,
∴从口袋中一次任取5个球,全是蓝球是不可能事件;
(3)从口袋中一次任意取出9个球,恰好红蓝白三种颜色的球都齐了是必然事件.
22.解:(1)当n=5或6时,这个事件必然发生;
(2)当n=1或2时,这个事件不可能发生;
(3)当n=3或4时,这个事件为可能发生.
23.解:答案不唯一
(1)如出现数字7朝上;(1分)
(2)如出现朝上的点数小于7;(1分)
(3)如出现朝上的点数为5.(1分)
24.解:(1)共有10种等可能出现的结果数,其中“是奇数”的有5种,“是偶数”的也有5种,因此“是奇数”“是偶数”的可能性都是50%,
(2)共有10种等可能出现的结果数,其中“是3的倍数”的有3种,“不是3的倍数”的7种,因此“是3的倍数”可能性是30%,“不是3的倍数”的可能性是70%,
(3)共有10种等可能出现的结果数,其中“是大于6的数”的有4种,“不是大于6的数”的有6种,因此“是大于6的数”可能性是40%,“不是大于6的数”的可能性是60%,
因此,猜数者选择“不是3的倍数”,这样获胜的可能性为70%,获胜的可能性最大.
25.解:因为转转盘所获得的购物券为:80×+50×+20×=16.5(元),(4分)
∵16.5元>15元
∴选择转转盘对顾客更合算.
26.解:(1)50×+30×+20×=11.875(元);
(2)虽然转动一次转盘,平均可以获得11.875元,但是获取的概率毕竟只有十六之七,领取10元购物券的机会却是百分之一百,虽然收益低,却更稳妥一些,因此说,这两种选择应该都是可以的.
27.解:(1)该抽奖方案符合厂家的设奖要求:
分别用黄1、黄2、白1、白2、白3表示这5个球,从中任意摸出2个球,可能出现的结果有:
(黄1,黄2)、(黄1,白1)、(黄1,白2)、(黄1,白3)、
(黄2,黄1)、(黄2,白1)、(黄2,白2)、(黄2,白3)、
(白1,黄1)、(白1,黄2)、(白1.白2)、(白1,白3)、
(白2,黄1)、(白2,黄2)、(白2,白1)、(白2,白3)、
(白3,黄1)、(白3,黄2)、(白3,白1)、(白3,白2)
共有20种,它们出现的可能性相同.
所有的结果中,满足摸到的2个球都是黄球(记为事件A)的结果有2种,即(黄1,黄2)或(黄2,黄1),
所以P(两黄球)==,即顾客获得大奖的概率为10%,获得小奖的概率为90%;
(2)本题答案不唯一,下列解法供参考.
如图,将转盘中圆心角为36°的扇形区域涂上黄色,其余的区域涂上白色,顾客每购买一台该型号电视机,可获得一次转动转盘的机会,任意转动这个转盘,当转盘停止时,指针指向黄色区域获得大奖,指向白色区域获得小奖.
