2021-2022学年华东师大新版七年级上册数学《第5章 相交线与平行线》单元测试卷(word解析版)
文档属性
| 名称 | 2021-2022学年华东师大新版七年级上册数学《第5章 相交线与平行线》单元测试卷(word解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 229.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-22 00:00:00 | ||
图片预览

文档简介
2021-2022学年华东师大新版七年级上册数学《第5章
相交线与平行线》单元测试卷
一.选择题
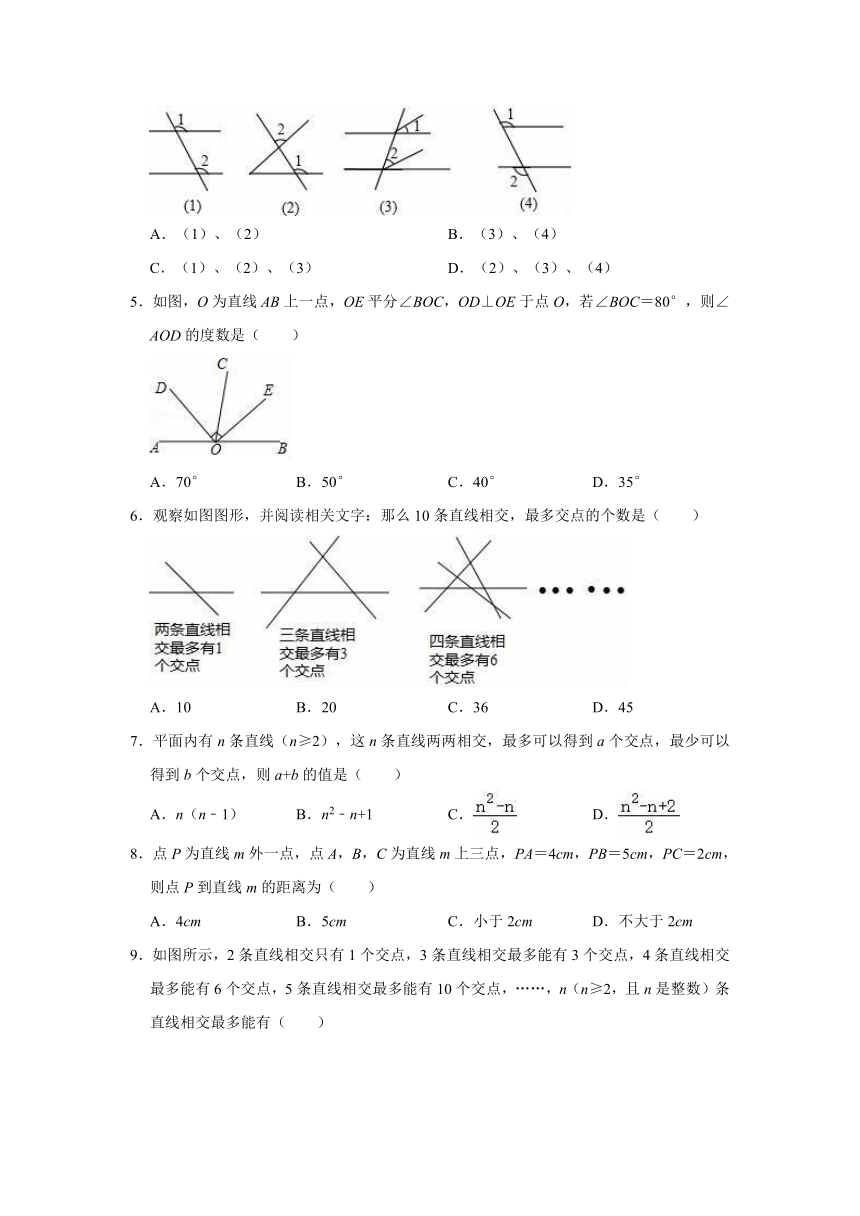
1.下面各图中的∠1与∠2是对顶角的是( )
A.
B.
C.
D.
2.如图,直线AB与直线CD相交于点O,OE⊥AB,垂足为O,∠EOD=∠AOC,则∠BOC=( )
A.150°
B.140°
C.130°
D.120°
3.如图,若村庄A要从河流l引水入村,则沿着垂线段AP铺设水管最节省材料,其依据是( )
A.两点之间,线段最短
B.垂线段最短
C.两点确定一条直线
D.在同一平面内,经过一点有并且只有一条直线与已知直线垂直
4.下列四幅图中,∠1和∠2是同位角的是( )
A.(1)、(2)
B.(3)、(4)
C.(1)、(2)、(3)
D.(2)、(3)、(4)
5.如图,O为直线AB上一点,OE平分∠BOC,OD⊥OE于点O,若∠BOC=80°,则∠AOD的度数是( )
A.70°
B.50°
C.40°
D.35°
6.观察如图图形,并阅读相关文字:那么10条直线相交,最多交点的个数是( )
A.10
B.20
C.36
D.45
7.平面内有n条直线(n≥2),这n条直线两两相交,最多可以得到a个交点,最少可以得到b个交点,则a+b的值是( )
A.n(n﹣1)
B.n2﹣n+1
C.
D.
8.点P为直线m外一点,点A,B,C为直线m上三点,PA=4cm,PB=5cm,PC=2cm,则点P到直线m的距离为( )
A.4cm
B.5cm
C.小于2cm
D.不大于2cm
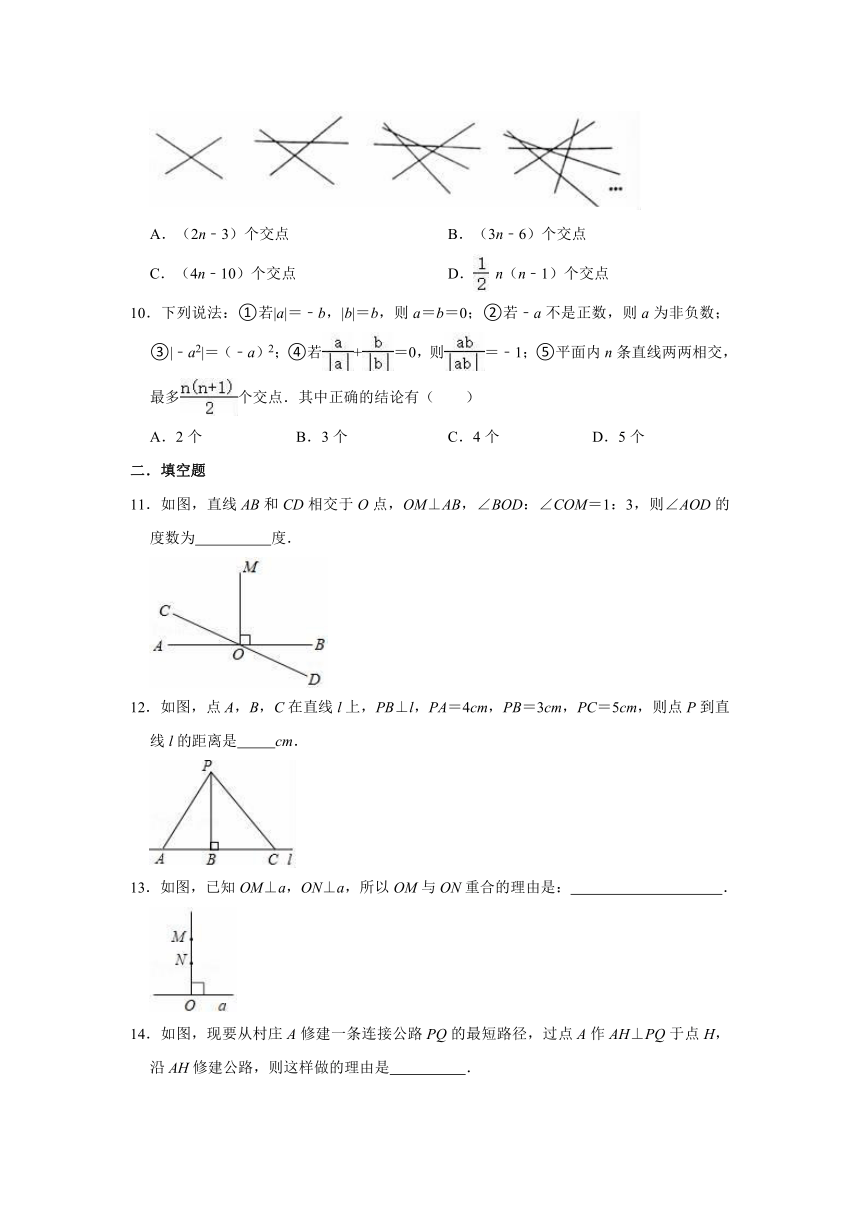
9.如图所示,2条直线相交只有1个交点,3条直线相交最多能有3个交点,4条直线相交最多能有6个交点,5条直线相交最多能有10个交点,……,n(n≥2,且n是整数)条直线相交最多能有( )
A.(2n﹣3)个交点
B.(3n﹣6)个交点
C.(4n﹣10)个交点
D.
n(n﹣1)个交点
10.下列说法:①若|a|=﹣b,|b|=b,则a=b=0;②若﹣a不是正数,则a为非负数;③|﹣a2|=(﹣a)2;④若+=0,则=﹣1;⑤平面内n条直线两两相交,最多个交点.其中正确的结论有( )
A.2个
B.3个
C.4个
D.5个
二.填空题
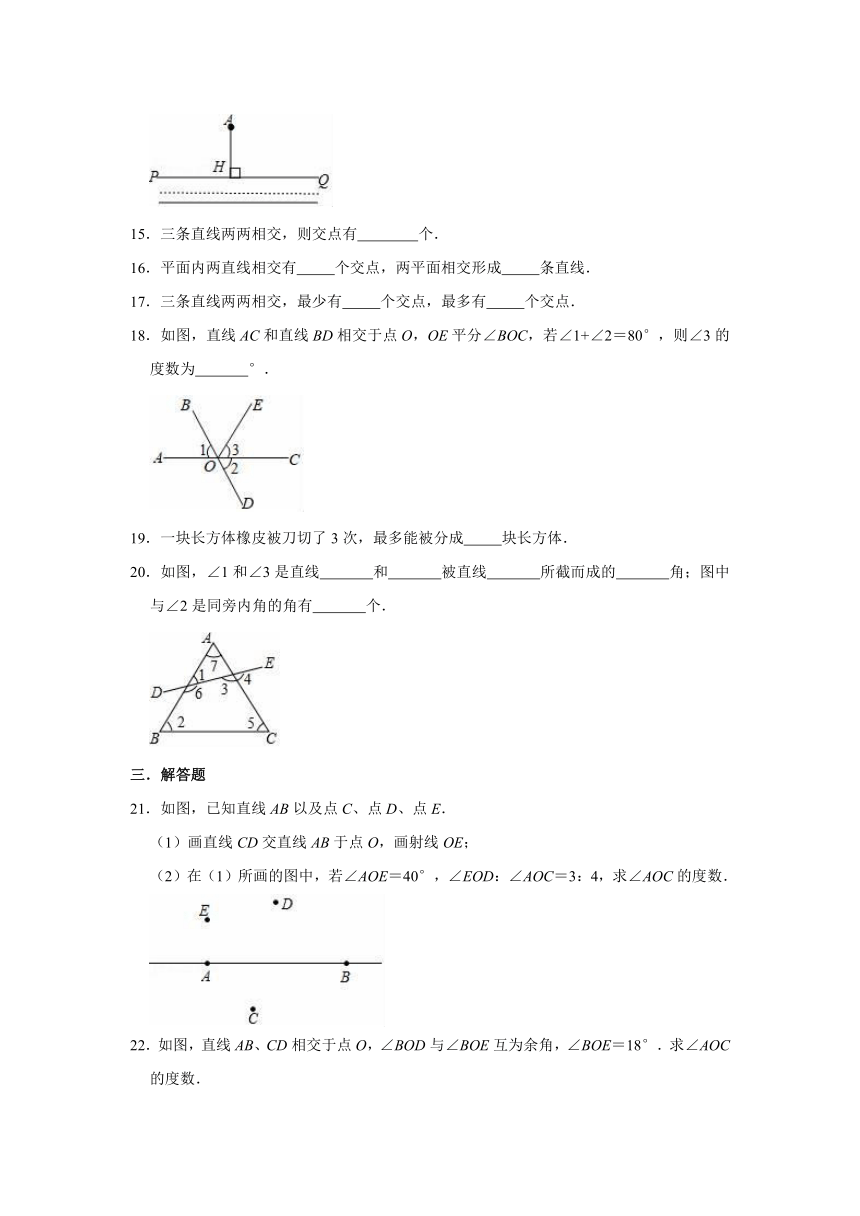
11.如图,直线AB和CD相交于O点,OM⊥AB,∠BOD:∠COM=1:3,则∠AOD的度数为
度.
12.如图,点A,B,C在直线l上,PB⊥l,PA=4cm,PB=3cm,PC=5cm,则点P到直线l的距离是
cm.
13.如图,已知OM⊥a,ON⊥a,所以OM与ON重合的理由是:
.
14.如图,现要从村庄A修建一条连接公路PQ的最短路径,过点A作AH⊥PQ于点H,沿AH修建公路,则这样做的理由是
.
15.三条直线两两相交,则交点有
个.
16.平面内两直线相交有
个交点,两平面相交形成
条直线.
17.三条直线两两相交,最少有
个交点,最多有
个交点.
18.如图,直线AC和直线BD相交于点O,OE平分∠BOC,若∠1+∠2=80°,则∠3的度数为
°.
19.一块长方体橡皮被刀切了3次,最多能被分成
块长方体.
20.如图,∠1和∠3是直线
和
被直线
所截而成的
角;图中与∠2是同旁内角的角有
个.
三.解答题
21.如图,已知直线AB以及点C、点D、点E.
(1)画直线CD交直线AB于点O,画射线OE;
(2)在(1)所画的图中,若∠AOE=40°,∠EOD:∠AOC=3:4,求∠AOC的度数.
22.如图,直线AB、CD相交于点O,∠BOD与∠BOE互为余角,∠BOE=18°.求∠AOC的度数.
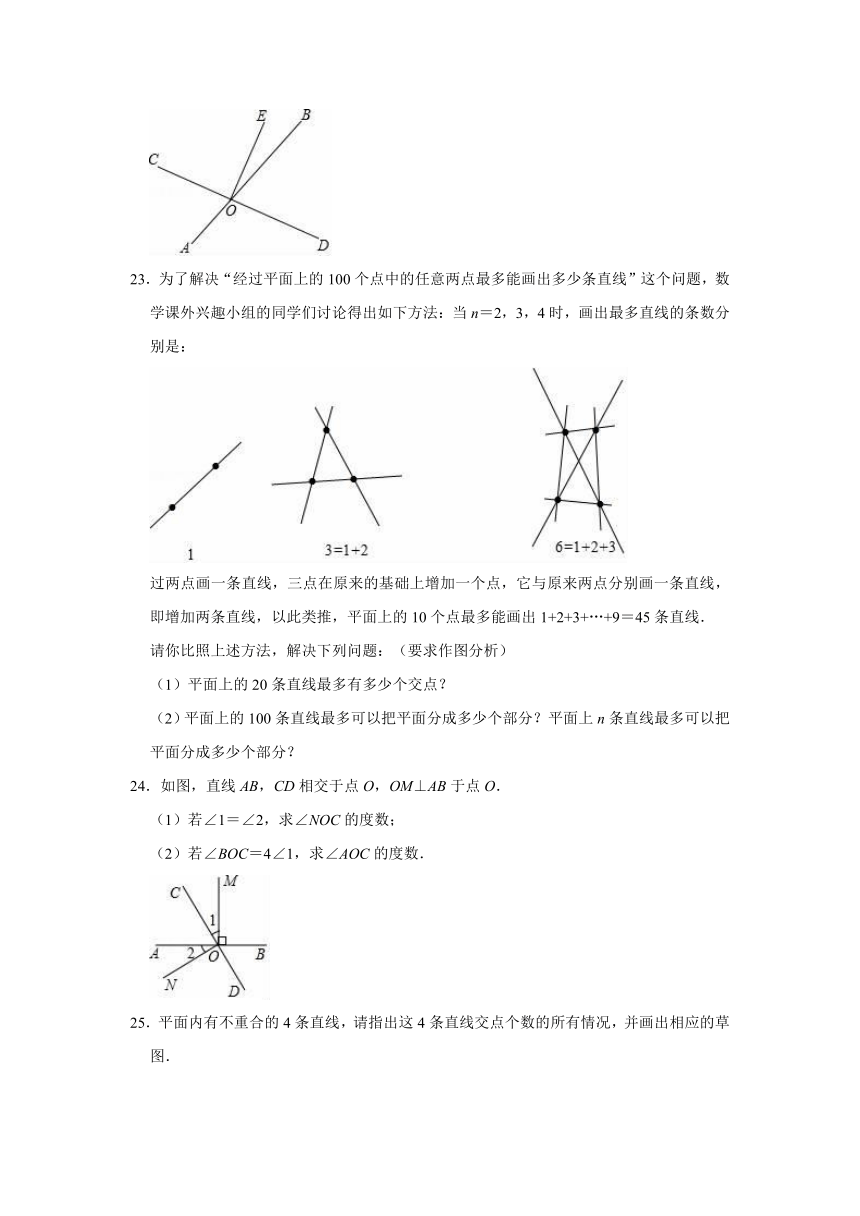
23.为了解决“经过平面上的100个点中的任意两点最多能画出多少条直线”这个问题,数学课外兴趣小组的同学们讨论得出如下方法:当n=2,3,4时,画出最多直线的条数分别是:
过两点画一条直线,三点在原来的基础上增加一个点,它与原来两点分别画一条直线,即增加两条直线,以此类推,平面上的10个点最多能画出1+2+3+…+9=45条直线.
请你比照上述方法,解决下列问题:(要求作图分析)
(1)平面上的20条直线最多有多少个交点?
(2)平面上的100条直线最多可以把平面分成多少个部分?平面上n条直线最多可以把平面分成多少个部分?
24.如图,直线AB,CD相交于点O,OM⊥AB于点O.
(1)若∠1=∠2,求∠NOC的度数;
(2)若∠BOC=4∠1,求∠AOC的度数.
25.平面内有不重合的4条直线,请指出这4条直线交点个数的所有情况,并画出相应的草图.
26.如图,已知直线AB,线段CO⊥AB于O,∠AOD=∠BOD,求∠COD的度数.
参考答案与试题解析
一.选择题
1.解:根据对顶角的定义可知:只有第4个图中的是对顶角,其它都不是.
故选:D.
2.解:∵∠COD=180°,OE⊥AB,
∴∠AOC+∠AOE+∠EOD=180°,∠AOE=90°,
∴∠AOC+∠EOD=90°,①
又∵∠EOD=∠AOC,②
由①、②得,∠AOC=60°,
∵∠BOC与∠AOC是邻补角,
∴∠BOC=180°﹣∠AOC=120°.
故选:D.
3.解:若村庄A要从河流l引水入村,则沿着垂线段AP铺设水管最节省材料,其依据是垂线段最短,
故选:B.
4.解:根据同位角的定义,图(1)、(2)中,∠1和∠2是同位角;
图(3)∠1、∠2的两边都不在同一条直线上,不是同位角;
图(4)∠1、∠2不在被截线同侧,不是同位角.
故选:A.
5.解:∵OD⊥OE于点O,
∴∠DOE=90°,
∴∠AOD+∠BOE=90°,
∵OE平分∠BOC,∠BOC=80°,
∴∠BOE=40°,
∴∠AOD=50°.
故选:B.
6.解:2条直线相交,只有1个交点,
3条直线相交,最多有3个交点,
4条直线相交,最多有6个交点,
…,
n条直线相交,最多有个交点,
n=10时,=45.
故选:D.
7.解:如图:2条直线相交有1个交点;
3条直线相交有1+2个交点;
4条直线相交有1+2+3个交点;
5条直线相交有1+2+3+4个交点;
6条直线相交有1+2+3+4+5个交点;
…
n条直线相交有1+2+3+4+5+…+(n﹣1)=个交点.
所以a=,而b=1,
∴a+b=.
故选:D.
8.解:当PC⊥m时,PC是点P到直线m的距离,即点P到直线m的距离2cm,
当PC不垂直直线m时,点P到直线m的距离小于PC的长,即点P到直线m的距离小于2cm,
综上所述:点P到直线m的距离不大于2cm,
故选:D.
9.解:2条直线相交有1个交点;
3条直线相交有1+2=3个交点;
4条直线相交有1+2+3=6个交点;
5条直线相交有1+2+3+4=10个交点;
6条直线相交有1+2+3+4+5=15个交点;
…
n条直线相交有1+2+3+4+5+…+(n﹣1)=n(n﹣1).
故选:D.
10.解:①若|a|=﹣b,|b|=b,则a=b=0,故本选项正确;
②若﹣a不是正数,则a为非负数,故本选项正确;
③|﹣a2|=(﹣a)2,故本选项正确;
④若+=0,则a,b异号,即=﹣1,故本选项正确;
⑤平面内n条直线两两相交,最多n(n﹣1)个交点,故本选项错误.
故选:C.
二.填空题
11.解:∵OM⊥AB,
∴∠BOM=90°,
∴∠BOD+∠COM=90°,
∵∠BOD:∠COM=1:3,
∴∠BOD=22.5°,
∵∠AOB=180°,
∴∠AOD=∠AOB﹣∠BOD=157.5°.
故答案为:157.5.
12.解:点P到直线l的距离是点P到直线l垂线段的长度,
∵PB⊥l,且PB=3cm,
∴点P到直线l的距离是3cm,
故答案为:3.
13.解:∵OM⊥a,ON⊥a,
∴OM与ON重合(在同一平面内,经过一点有且只有一条直线与已知直线垂直),
故答案为:在同一平面内,经过一点有且只有一条直线与已知直线垂直.
14.解:∵从直线外一点到这条直线上各点所连线段中,垂线段最短,
∴过点A作AH⊥PQ于点H,这样做的理由是垂线段最短.
故答案为:垂线段最短.
15.解:如图所示:
故三条直线两两相交,则交点有1或3个.
故答案为:1或3.
16.解:在同一平面内,直线相交有只能有一个交点,而平面相交则是一条直线,且只有一条.
17.解:如图所示:
两两相交的直线,其最少有1个交点,即三条直线相交于一点;
最多有三个交点,即其构成一个三角形,共三个交点.
故答案为1,3.
18.解:∵∠1=∠2,∠1+∠2=80°,
∴∠1=∠2=40°,
∴∠BOC=180°﹣∠1=140°,
又∵OE平分∠BOC,
∴∠3=×140°=70°.
故答案为:70.
19.解:长方体橡皮可以想象为立体图形,第一次最多切2块,第二次在第一次的基础上增加2倍,第三次在第二次的基础上又增加2倍,故最多能被分成8块.
20.解:∠1和∠3是直线AB和AC被直线DE所截而成的内错角;图中与∠2
是同旁内角的角有∠6、∠5、∠7,共3个,
故答案为:AB、AC、DE、内错,3.
三.解答题
21.解:(1)如图所示,直线CD,射线OE即为所求;
(2)∵∠EOD:∠AOC=3:4,
∴设∠EOD=3x,∠AOC=4x,
∵∠BOD=∠AOC,
∴∠BOD=4x,
∵∠AOB=180°,
∴40°+3x+4x=180°,
∴x=20°,
∴∠AOC=4x=80°.
22.解:∵∠BOD与∠BOE互为余角,
∴∠BOD+∠EOB=90°,
∵∠BOE=18°,
∴∠BOD=90°﹣18°=72°,
∴∠AOC=∠BOD=72°.
23.解:(1)当有2,3,4条直线时最多交点的个数分别是:
∴20条直线最多有1+2+3+…+19=190个交点;
(2)当有1,2,3条直线时最多可把平面分成的部分分别是:
∴100条直线最多可把平面分成
1+(1+2+3+…+100)=5051个部分,
同理n条直线最多可把平面分成
1+(1+2+3+…+n)=1+=.
24.解:(1)∵OM⊥AB于点O,
∴∠AOM=∠BOM=90°,
∴∠1+∠AOC=90°,
∵∠2=∠1,
∴∠2+∠AOC=90°,
∴∠NOC=90°;
(2)∵OM⊥AB于点O,
∴∠AOM=∠BOM=90°,
∵∠BOC=4∠1,
∴∠BOM=∠BOC﹣∠1=4∠1﹣∠1=90°,
∴∠1=30°,
∴∠AOC=∠AOM﹣∠1=90°﹣30°=60°.
25.解:(1)当四条直线平行时,无交点,
(2)当三条平行,另一条与这三条不平行时,有3个交点,
(3)当两两直线平行时,有4个交点,
(4)当有两条直线平行,而另两条不平行时,有5个交点,
(5)当四条直线同交于一点时,只有1个交点,
(6)当四条直线两两相交,且不过同一点时,有6个交点,
(7)当有两条直线平行,而另两条不平行并且交点在平行线上时,有3个交点,
(8)当三条直线交于一点,第四条直线与其它三条直线有三个交点时,共有4个交点,
故4条直线交点个数为:0或1或3或4或5或6.
26.解:∵∠AOD+∠BOD=180°,∠AOD=∠BOD,
∴∠AOD+2∠AOD=180°,
∴∠AOD=60°,
又∵CO⊥AB,
∴∠AOC=90°,
∴∠COD=90°﹣60°=30°.
相交线与平行线》单元测试卷
一.选择题
1.下面各图中的∠1与∠2是对顶角的是( )
A.
B.
C.
D.
2.如图,直线AB与直线CD相交于点O,OE⊥AB,垂足为O,∠EOD=∠AOC,则∠BOC=( )
A.150°
B.140°
C.130°
D.120°
3.如图,若村庄A要从河流l引水入村,则沿着垂线段AP铺设水管最节省材料,其依据是( )
A.两点之间,线段最短
B.垂线段最短
C.两点确定一条直线
D.在同一平面内,经过一点有并且只有一条直线与已知直线垂直
4.下列四幅图中,∠1和∠2是同位角的是( )
A.(1)、(2)
B.(3)、(4)
C.(1)、(2)、(3)
D.(2)、(3)、(4)
5.如图,O为直线AB上一点,OE平分∠BOC,OD⊥OE于点O,若∠BOC=80°,则∠AOD的度数是( )
A.70°
B.50°
C.40°
D.35°
6.观察如图图形,并阅读相关文字:那么10条直线相交,最多交点的个数是( )
A.10
B.20
C.36
D.45
7.平面内有n条直线(n≥2),这n条直线两两相交,最多可以得到a个交点,最少可以得到b个交点,则a+b的值是( )
A.n(n﹣1)
B.n2﹣n+1
C.
D.
8.点P为直线m外一点,点A,B,C为直线m上三点,PA=4cm,PB=5cm,PC=2cm,则点P到直线m的距离为( )
A.4cm
B.5cm
C.小于2cm
D.不大于2cm
9.如图所示,2条直线相交只有1个交点,3条直线相交最多能有3个交点,4条直线相交最多能有6个交点,5条直线相交最多能有10个交点,……,n(n≥2,且n是整数)条直线相交最多能有( )
A.(2n﹣3)个交点
B.(3n﹣6)个交点
C.(4n﹣10)个交点
D.
n(n﹣1)个交点
10.下列说法:①若|a|=﹣b,|b|=b,则a=b=0;②若﹣a不是正数,则a为非负数;③|﹣a2|=(﹣a)2;④若+=0,则=﹣1;⑤平面内n条直线两两相交,最多个交点.其中正确的结论有( )
A.2个
B.3个
C.4个
D.5个
二.填空题
11.如图,直线AB和CD相交于O点,OM⊥AB,∠BOD:∠COM=1:3,则∠AOD的度数为
度.
12.如图,点A,B,C在直线l上,PB⊥l,PA=4cm,PB=3cm,PC=5cm,则点P到直线l的距离是
cm.
13.如图,已知OM⊥a,ON⊥a,所以OM与ON重合的理由是:
.
14.如图,现要从村庄A修建一条连接公路PQ的最短路径,过点A作AH⊥PQ于点H,沿AH修建公路,则这样做的理由是
.
15.三条直线两两相交,则交点有
个.
16.平面内两直线相交有
个交点,两平面相交形成
条直线.
17.三条直线两两相交,最少有
个交点,最多有
个交点.
18.如图,直线AC和直线BD相交于点O,OE平分∠BOC,若∠1+∠2=80°,则∠3的度数为
°.
19.一块长方体橡皮被刀切了3次,最多能被分成
块长方体.
20.如图,∠1和∠3是直线
和
被直线
所截而成的
角;图中与∠2是同旁内角的角有
个.
三.解答题
21.如图,已知直线AB以及点C、点D、点E.
(1)画直线CD交直线AB于点O,画射线OE;
(2)在(1)所画的图中,若∠AOE=40°,∠EOD:∠AOC=3:4,求∠AOC的度数.
22.如图,直线AB、CD相交于点O,∠BOD与∠BOE互为余角,∠BOE=18°.求∠AOC的度数.
23.为了解决“经过平面上的100个点中的任意两点最多能画出多少条直线”这个问题,数学课外兴趣小组的同学们讨论得出如下方法:当n=2,3,4时,画出最多直线的条数分别是:
过两点画一条直线,三点在原来的基础上增加一个点,它与原来两点分别画一条直线,即增加两条直线,以此类推,平面上的10个点最多能画出1+2+3+…+9=45条直线.
请你比照上述方法,解决下列问题:(要求作图分析)
(1)平面上的20条直线最多有多少个交点?
(2)平面上的100条直线最多可以把平面分成多少个部分?平面上n条直线最多可以把平面分成多少个部分?
24.如图,直线AB,CD相交于点O,OM⊥AB于点O.
(1)若∠1=∠2,求∠NOC的度数;
(2)若∠BOC=4∠1,求∠AOC的度数.
25.平面内有不重合的4条直线,请指出这4条直线交点个数的所有情况,并画出相应的草图.
26.如图,已知直线AB,线段CO⊥AB于O,∠AOD=∠BOD,求∠COD的度数.
参考答案与试题解析
一.选择题
1.解:根据对顶角的定义可知:只有第4个图中的是对顶角,其它都不是.
故选:D.
2.解:∵∠COD=180°,OE⊥AB,
∴∠AOC+∠AOE+∠EOD=180°,∠AOE=90°,
∴∠AOC+∠EOD=90°,①
又∵∠EOD=∠AOC,②
由①、②得,∠AOC=60°,
∵∠BOC与∠AOC是邻补角,
∴∠BOC=180°﹣∠AOC=120°.
故选:D.
3.解:若村庄A要从河流l引水入村,则沿着垂线段AP铺设水管最节省材料,其依据是垂线段最短,
故选:B.
4.解:根据同位角的定义,图(1)、(2)中,∠1和∠2是同位角;
图(3)∠1、∠2的两边都不在同一条直线上,不是同位角;
图(4)∠1、∠2不在被截线同侧,不是同位角.
故选:A.
5.解:∵OD⊥OE于点O,
∴∠DOE=90°,
∴∠AOD+∠BOE=90°,
∵OE平分∠BOC,∠BOC=80°,
∴∠BOE=40°,
∴∠AOD=50°.
故选:B.
6.解:2条直线相交,只有1个交点,
3条直线相交,最多有3个交点,
4条直线相交,最多有6个交点,
…,
n条直线相交,最多有个交点,
n=10时,=45.
故选:D.
7.解:如图:2条直线相交有1个交点;
3条直线相交有1+2个交点;
4条直线相交有1+2+3个交点;
5条直线相交有1+2+3+4个交点;
6条直线相交有1+2+3+4+5个交点;
…
n条直线相交有1+2+3+4+5+…+(n﹣1)=个交点.
所以a=,而b=1,
∴a+b=.
故选:D.
8.解:当PC⊥m时,PC是点P到直线m的距离,即点P到直线m的距离2cm,
当PC不垂直直线m时,点P到直线m的距离小于PC的长,即点P到直线m的距离小于2cm,
综上所述:点P到直线m的距离不大于2cm,
故选:D.
9.解:2条直线相交有1个交点;
3条直线相交有1+2=3个交点;
4条直线相交有1+2+3=6个交点;
5条直线相交有1+2+3+4=10个交点;
6条直线相交有1+2+3+4+5=15个交点;
…
n条直线相交有1+2+3+4+5+…+(n﹣1)=n(n﹣1).
故选:D.
10.解:①若|a|=﹣b,|b|=b,则a=b=0,故本选项正确;
②若﹣a不是正数,则a为非负数,故本选项正确;
③|﹣a2|=(﹣a)2,故本选项正确;
④若+=0,则a,b异号,即=﹣1,故本选项正确;
⑤平面内n条直线两两相交,最多n(n﹣1)个交点,故本选项错误.
故选:C.
二.填空题
11.解:∵OM⊥AB,
∴∠BOM=90°,
∴∠BOD+∠COM=90°,
∵∠BOD:∠COM=1:3,
∴∠BOD=22.5°,
∵∠AOB=180°,
∴∠AOD=∠AOB﹣∠BOD=157.5°.
故答案为:157.5.
12.解:点P到直线l的距离是点P到直线l垂线段的长度,
∵PB⊥l,且PB=3cm,
∴点P到直线l的距离是3cm,
故答案为:3.
13.解:∵OM⊥a,ON⊥a,
∴OM与ON重合(在同一平面内,经过一点有且只有一条直线与已知直线垂直),
故答案为:在同一平面内,经过一点有且只有一条直线与已知直线垂直.
14.解:∵从直线外一点到这条直线上各点所连线段中,垂线段最短,
∴过点A作AH⊥PQ于点H,这样做的理由是垂线段最短.
故答案为:垂线段最短.
15.解:如图所示:
故三条直线两两相交,则交点有1或3个.
故答案为:1或3.
16.解:在同一平面内,直线相交有只能有一个交点,而平面相交则是一条直线,且只有一条.
17.解:如图所示:
两两相交的直线,其最少有1个交点,即三条直线相交于一点;
最多有三个交点,即其构成一个三角形,共三个交点.
故答案为1,3.
18.解:∵∠1=∠2,∠1+∠2=80°,
∴∠1=∠2=40°,
∴∠BOC=180°﹣∠1=140°,
又∵OE平分∠BOC,
∴∠3=×140°=70°.
故答案为:70.
19.解:长方体橡皮可以想象为立体图形,第一次最多切2块,第二次在第一次的基础上增加2倍,第三次在第二次的基础上又增加2倍,故最多能被分成8块.
20.解:∠1和∠3是直线AB和AC被直线DE所截而成的内错角;图中与∠2
是同旁内角的角有∠6、∠5、∠7,共3个,
故答案为:AB、AC、DE、内错,3.
三.解答题
21.解:(1)如图所示,直线CD,射线OE即为所求;
(2)∵∠EOD:∠AOC=3:4,
∴设∠EOD=3x,∠AOC=4x,
∵∠BOD=∠AOC,
∴∠BOD=4x,
∵∠AOB=180°,
∴40°+3x+4x=180°,
∴x=20°,
∴∠AOC=4x=80°.
22.解:∵∠BOD与∠BOE互为余角,
∴∠BOD+∠EOB=90°,
∵∠BOE=18°,
∴∠BOD=90°﹣18°=72°,
∴∠AOC=∠BOD=72°.
23.解:(1)当有2,3,4条直线时最多交点的个数分别是:
∴20条直线最多有1+2+3+…+19=190个交点;
(2)当有1,2,3条直线时最多可把平面分成的部分分别是:
∴100条直线最多可把平面分成
1+(1+2+3+…+100)=5051个部分,
同理n条直线最多可把平面分成
1+(1+2+3+…+n)=1+=.
24.解:(1)∵OM⊥AB于点O,
∴∠AOM=∠BOM=90°,
∴∠1+∠AOC=90°,
∵∠2=∠1,
∴∠2+∠AOC=90°,
∴∠NOC=90°;
(2)∵OM⊥AB于点O,
∴∠AOM=∠BOM=90°,
∵∠BOC=4∠1,
∴∠BOM=∠BOC﹣∠1=4∠1﹣∠1=90°,
∴∠1=30°,
∴∠AOC=∠AOM﹣∠1=90°﹣30°=60°.
25.解:(1)当四条直线平行时,无交点,
(2)当三条平行,另一条与这三条不平行时,有3个交点,
(3)当两两直线平行时,有4个交点,
(4)当有两条直线平行,而另两条不平行时,有5个交点,
(5)当四条直线同交于一点时,只有1个交点,
(6)当四条直线两两相交,且不过同一点时,有6个交点,
(7)当有两条直线平行,而另两条不平行并且交点在平行线上时,有3个交点,
(8)当三条直线交于一点,第四条直线与其它三条直线有三个交点时,共有4个交点,
故4条直线交点个数为:0或1或3或4或5或6.
26.解:∵∠AOD+∠BOD=180°,∠AOD=∠BOD,
∴∠AOD+2∠AOD=180°,
∴∠AOD=60°,
又∵CO⊥AB,
∴∠AOC=90°,
∴∠COD=90°﹣60°=30°.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
