2021-2022学年苏科新版八年级上册数学《第6章 一次函数》单元测试卷(word解析版)
文档属性
| 名称 | 2021-2022学年苏科新版八年级上册数学《第6章 一次函数》单元测试卷(word解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 196.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-22 16:14:38 | ||
图片预览




文档简介
2021-2022学年苏科新版八年级上册数学《第6章
一次函数》单元测试卷
一.选择题
1.我们知道,圆的周长公式是:C=2πr,那么在这个公式中,以下关于变量和常量的说法正确的是( )
A.2是常量,C,π,r是变量
B.2π是常量,C,r是变量
C.2是常量,r是变量
D.2是常量,C,r是变量
2.如果用总长为60m的篱笆围成一个长方形场地,设长方形的面积为S(m2),周长为p(m),一边长为a(m),那么S,p,a中是变量的是( )
A.S和p
B.S和a
C.p和a
D.S,p,a
3.下列曲线中,表示y是x的函数的是( )
A.
B.
C.
D.
4.据测试,拧不紧的水龙头每分钟滴出100滴水,每滴水约0.05毫升.小明洗手后没有把水龙头拧紧,水龙头以测试速度滴水,当小明离开x分钟后,水龙头滴水y毫升水,则y与x之间的函数关系式是( )
A.y=0.05x
B.y=5x
C.y=100x
D.y=0.05x+100
5.函数y=中自变量x的取值范围是( )
A.x>2
B.x≥2
C.x≤2
D.x≠2
6.关于函数y=﹣2x+1,下列结论正确的是( )
A.图象必经过(﹣2,1)
B.y随x的增大而增大
C.图象经过第一、二、三象限
D.当x>时,y<0
7.函数的零点是指使函数值等于零的自变量的值,则下列函数中存在零点的是( )
A.y=x2+x+2
B.y=+1
C.y=x+
D.y=|x|﹣1
8.一次函数y=(m﹣2)xn﹣1+3是关于x的一次函数,则m,n的值为( )
A.m≠2且n=2
B.m=2且n=2
C.m≠2且n=1
D.m=2且n=1
9.假设汽车匀速行驶在高速公路上,那么在下列各量中,变量的个数是( )
①行驶速度;②行驶时间;③行驶路程;④汽车油箱中的剩余油量.
A.1个
B.2个
C.3个
D.4个
10.一个蓄水池有水50m3,打开放水闸门匀速放水,水池中的水量和放水时间的关系如表,下面说法不正确的是( )
放水时间(min)
1
2
3
4
…
水池中水量(m3)
48
46
44
42
…
A.放水时间是自变量,水池中的水量是因变量
B.每分钟放水2m3
C.放水25min后,水池中的水全部放完
D.放水10min后,水池中还有水28m3
二.填空题
11.“早穿皮袄,午穿纱,围着火炉吃西瓜.”这句谚语反映了我国新疆地区一天中,
随
变化而变化,其中自变量是
,因变量是
.
12.如图,圆柱的高是3cm,当圆柱的底面半径由小到大变化时,圆柱的体积也随之发生了变化.
(1)在这个变化中,自变量是
,因变量是
;
(2)当底面半径由1cm变化到10cm时,圆柱的体积增加了
cm3.
13.对于圆的周长公式c=2πr,其中自变量是
,因变量是
.
14.某汽车生产厂对其生产的A型汽车进行油耗试验,试验中汽车为匀速行驶,在行驶过程中,油箱的余油量y(升)与行驶时间t(小时)之间的关系如下表:
t(小时)
0
1
2
3
y(升)
100
92
84
76
由表格中y与t的关系可知,当汽车行驶
小时,油箱的余油量为40升.
15.已知点(﹣2,y1),(2,y2)都在直线y=2x﹣3上,则y1
y2.(填“<”或“>”或“=”)
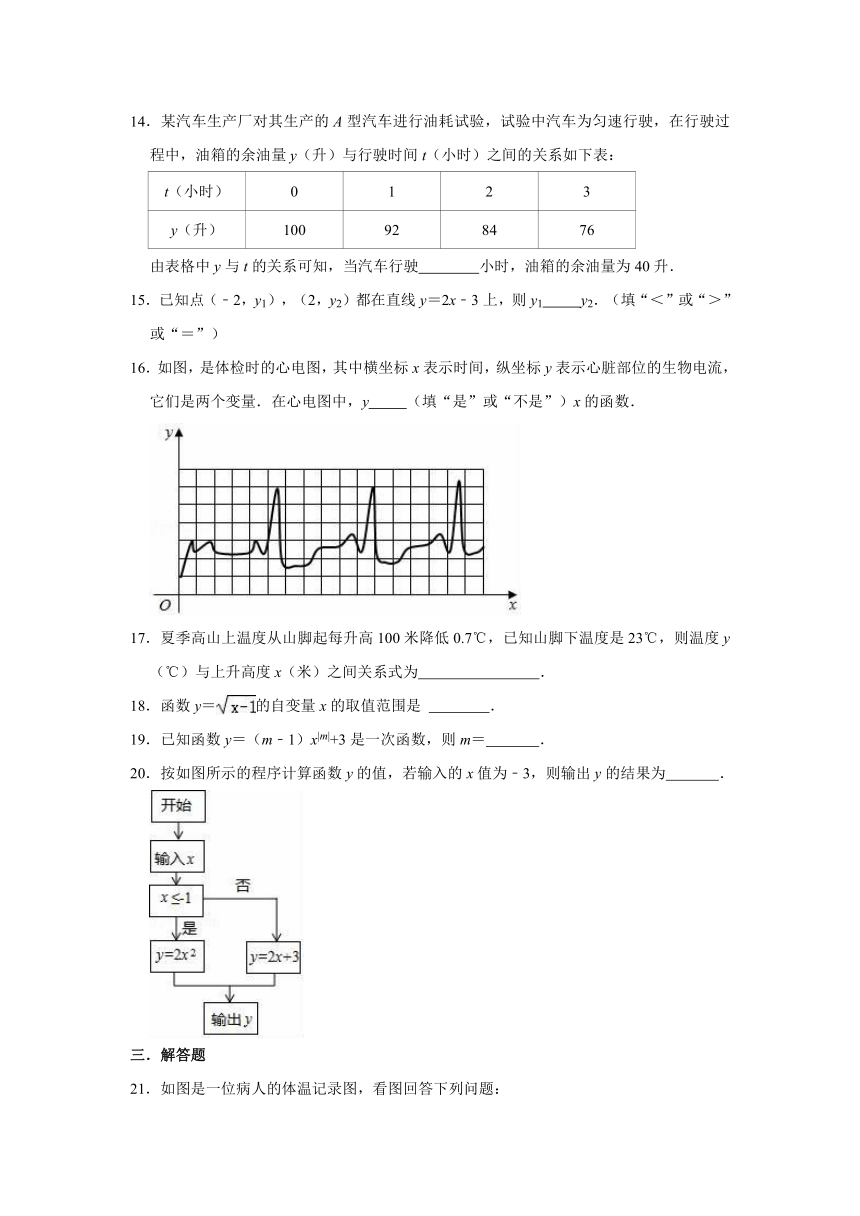
16.如图,是体检时的心电图,其中横坐标x表示时间,纵坐标y表示心脏部位的生物电流,它们是两个变量.在心电图中,y
(填“是”或“不是”)x的函数.
17.夏季高山上温度从山脚起每升高100米降低0.7℃,已知山脚下温度是23℃,则温度y(℃)与上升高度x(米)之间关系式为
.
18.函数y=的自变量x的取值范围是
.
19.已知函数y=(m﹣1)x|m|+3是一次函数,则m=
.
20.按如图所示的程序计算函数y的值,若输入的x值为﹣3,则输出y的结果为
.
三.解答题
21.如图是一位病人的体温记录图,看图回答下列问题:
(1)自变量是
,因变量是
;
(2)护士每隔
小时给病人量一次体温;
(3)这位病人的最高体温是
摄氏度,最低体温是
摄氏度;
(4)他在4月8日12时的体温是
摄氏度;
(5)图中的横虚线表示
;
22.在函数y=中,求自变量x的取值范围.
23.已知y是x的函数,如表是y与x的几组对应值.
x
…
﹣5
﹣4
﹣3
﹣2
0
1
2
3
4
5
…
y
…
1.969
1.938
1.875
1.75
1
0
﹣2
﹣1.5
0
2.5
…
小明根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.
下面是小明的探究过程,请补充完整:
(1)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(2)根据画出的函数图象,写出:
①x=﹣1对应的函数值y约为
;
②该函数的一条性质:
.
24.写出下列各问题中的关系式中的常量与变量:
(1)分针旋转一周内,旋转的角度n(度)与旋转所需要的时间t(分)之间的关系式n=6t;
(2)一辆汽车以40千米/时的速度向前匀速直线行驶时,汽车行驶的路程S(千米)与行驶时间t(时)之间的关系式s=40t.
25.希望中学学生从2014年12月份开始每周喝营养牛奶,单价为2元/盒,总价y元随营养牛奶盒数x变化.指出其中的常量与变量,自变量与函数,并写出表示函数与自变量关系的式子.
26.阅读下面的材料:
如果函数y=f(x)满足:对于自变量x的取值范围内的任意x1,x2,
(1)若x1<x2,都有f(x1)<f(x2),则称f(x)是增函数;
(2)若x1<x2,都有f(x1)>f(x2),则称f(x)是减函数.
例题:证明函数f(x)=(x>0)是减函数.
证明:设0<x1<x2,
f(x1)﹣f(x2)=﹣==.
∵0<x1<x2,
∴x2﹣x1>0,x1x2>0.
∴>0.即f(x1)﹣f(x2)>0.
∴f(x1)>f(x2).
∴函数f(x)=(x>0)是减函数.
根据以上材料,解答下面的问题:
已知函数f(x)=+2x(x<0),
f(﹣1)=+(﹣2)=﹣1,f(﹣2)=+(﹣4)=﹣
(1)计算:f(﹣3)=
,f(﹣4)=
;
(2)猜想:函数f(x)=+2x(x<0)是
函数(填“增”或“减”);
(3)请仿照例题证明你的猜想.
27.有研究表明,声音在空气中的传播速度与空气的温度有关,当空气的温度变化,声音的传播速度也将随着变化.声音在空气中传播速度与空气温度关系一些数据(如下表格)
温度/℃
…
﹣20
﹣10
0
10
20
30
…
声速/(m/s)
…
318
324
330
336
342
348
…
(1)指出在这个变化过程中的自变量和因变量;
(2)当声音在空气中传播速度为342m/s时,此时空气的温度是多少?
(3)该数据表明:空气的温度每升高10℃,声音的传播速度将增大(或减少)多少?
(4)用y表示声音在空气中的传播速度,x表示空气温度,根据(3)中你发现的规律,直接写出y与x之间的关系式.
参考答案与试题解析
一.选择题
1.解:圆的周长计算公式是c=2πr,C和r是变量,2、π是常量,
故选:B.
2.解:∵篱笆的总长为60米,
∴周长p是定值,而面积S和一边长a是变量,
故选:B.
3.解:A、不能表示y是x的函数,故此选项不合题意;
B、不能表示y是x的函数,故此选项不合题意;
C、不能表示y是x的函数,故此选项不合题意;
D、能表示y是x的函数,故此选项符合题意;
故选:D.
4.解:根据题意可得:y=100×0.05x,
即y=5x.
故选:B.
5.解:由题意得,x﹣2≥0,
解得x≥2.
故选:B.
6.解:根据一次函数的性质,依次分析可得,
A、x=﹣2时,y=﹣2×﹣2+1=5,故图象必经过(﹣2,5),故错误,
B、k<0,则y随x的增大而减小,故错误,
C、k=﹣2<0,b=1>0,则图象经过第一、二、四象限,故错误,
D、当x>时,y<0,正确;
故选:D.
7.解:当y=0时,
方程x2+x+2=0无实数根,因此选项A不符合题意;
方程+1=0无实数根,因此选项B不符合题意;
方程x+=0无实数根,因此选项C不符合题意;
方程|x|﹣1=0的解为x=±1,因此选项D符合题意,
故选:D.
8.解:∵一次函数y=(m﹣2)xn﹣1+3是关于x的一次函数,
∴n﹣1=1且m﹣2≠0,
解得:n=2且m≠2.
故选:A.
9.解:∵汽车匀速行驶在高速公路上,速度是常量,随着时间的变化,行驶时间,行驶路程,剩余油量随之变化,
∴②行驶时间;③行驶路程;④汽车油箱中的剩余油量是变量.
故选:C.
10.解:根据表格数据知:蓄水池原有水50m3,每分钟水闸排水2m3.
水池剩余水量可以看以时间为自变量的函数故A正确.
∵每分钟水闸排水2m3.故B正确.
∵2×25=50.故C正确
放水10分钟,还剩水:50﹣2×10=30(m3).
故D错误.
故选:D.
二.填空题
11.解:“早穿皮袄,午穿纱,围着火炉吃西瓜.”这句谚语反映了我国新疆地区一天中,温度随时间变化而变化,其中自变量是:时间,因变量是:温度.
故答案是:温度、时间、时间、温度.
12.解:(1)根据函数的定义可知,对于底面半径的每个值,体积按照一定的法则有一个确定的值与之对应,所以自变量是:半径,因变量是:体积.
(2)体积增加了(π×102﹣π×12)×3=297πcm3.
故答案为:(1)半径,体积;(2)297π.
13.解:自变量是r,因变量是c.
14.解:由题意可得:y=100﹣8t,
当y=40时,40=100﹣8t
解得:t=7.5.
故答案为:7.5.
15.解:∵k=2>0,
∴y随x的增大而增大,
又∵﹣2<2,
∴y1<y2.
故答案为:<.
16.解:∵两个变量x和y,变量y随x的变化而变化,
且对于每一个x,y都有唯一值与之对应,
∴y是x的函数.
故答案为:是.
17.解:每升高100m降低0.7℃,则每上升1m,降低0.007℃,
则关系式为:y=23﹣0.007x;
故答案为:y=23﹣0.007x.
18.解:根据题意得,x﹣1≥0,
解得x≥1.
故答案为x≥1.
19.解:一次函数y=kx+b的定义条件是:k、b为常数,k≠0,自变量次数为1.
则得到|m|=1,m=±1,
∵m﹣1≠0,
∴m≠1,m=﹣1.
20.解:∵﹣3<﹣1,
把x=﹣3代入y=2x2,得y=2×9=18,
故答案为:18.
三.解答题
21.解:(1)自变量是时间,因变量是体温;
(2)护士每隔6小时给病人量一次体温;
(3)这位病人的最高体温是39.5摄氏度,最低体温是36.8摄氏度;
(4)他在4月8日12时的体温是37.5摄氏度;
(5)图中的横虚线表示人的正常体温;
故答案为:时间;体温;6;39.5;36.8;37.5;人的正常体温.
22.解:根据题意得:,
解得:﹣2≤x≤0或6≤x≤8.
故自变量x的取值范围是﹣2≤x≤0或6≤x≤8.
23.解:(1)如右图所求;
(2)①x=﹣1对应的函数值y约为1.5;
②当x<2时,y随x的增大而减小,(答案不唯一);
故答案为:1.5,当x<2时,y随x的增大而减小.
24.解:(1)常量:6;变量:n,t.
(2)常量:40;变量:s,t.
25.解:由题意得:
y=2x,
常量是2,变量是x、y,
x是自变量,y是x的函数.
26.解:(1)∵f(x)=+2x(x<0),
∴f(﹣3)=+2×(﹣3)=﹣,f(﹣4)=+2×(﹣4)=﹣
故答案为:﹣,﹣;
(2)∵﹣4<﹣3,f(﹣4)<f(﹣3)
∴函数f(x)=+2x(x<0)是增函数,
故答案为:增;
(3)设x1<x2<0,
∵f(x1)﹣f(x2)=+2x1﹣﹣2x2=(x1﹣x2)(2﹣)
∵x1<x2<0,
∴x1﹣x2<0,x1+x2<0,
∴f(x1)﹣f(x2)<0
∴f(x1)<f(x2)
∴函数f(x)=+2x(x<0)是增函数.
27.解:(1)自变量是温度,因变量是声速;
(2)由图表中数据可得出,当声音在空气中传播速度为342m/s时,此时空气的温度是20℃;
(3)利用表格中数据得出;空气的温度每升高10℃,声音的传播速度将增大6m/s;
(4)由图表中数据可得出:y=0.6x+330.
一次函数》单元测试卷
一.选择题
1.我们知道,圆的周长公式是:C=2πr,那么在这个公式中,以下关于变量和常量的说法正确的是( )
A.2是常量,C,π,r是变量
B.2π是常量,C,r是变量
C.2是常量,r是变量
D.2是常量,C,r是变量
2.如果用总长为60m的篱笆围成一个长方形场地,设长方形的面积为S(m2),周长为p(m),一边长为a(m),那么S,p,a中是变量的是( )
A.S和p
B.S和a
C.p和a
D.S,p,a
3.下列曲线中,表示y是x的函数的是( )
A.
B.
C.
D.
4.据测试,拧不紧的水龙头每分钟滴出100滴水,每滴水约0.05毫升.小明洗手后没有把水龙头拧紧,水龙头以测试速度滴水,当小明离开x分钟后,水龙头滴水y毫升水,则y与x之间的函数关系式是( )
A.y=0.05x
B.y=5x
C.y=100x
D.y=0.05x+100
5.函数y=中自变量x的取值范围是( )
A.x>2
B.x≥2
C.x≤2
D.x≠2
6.关于函数y=﹣2x+1,下列结论正确的是( )
A.图象必经过(﹣2,1)
B.y随x的增大而增大
C.图象经过第一、二、三象限
D.当x>时,y<0
7.函数的零点是指使函数值等于零的自变量的值,则下列函数中存在零点的是( )
A.y=x2+x+2
B.y=+1
C.y=x+
D.y=|x|﹣1
8.一次函数y=(m﹣2)xn﹣1+3是关于x的一次函数,则m,n的值为( )
A.m≠2且n=2
B.m=2且n=2
C.m≠2且n=1
D.m=2且n=1
9.假设汽车匀速行驶在高速公路上,那么在下列各量中,变量的个数是( )
①行驶速度;②行驶时间;③行驶路程;④汽车油箱中的剩余油量.
A.1个
B.2个
C.3个
D.4个
10.一个蓄水池有水50m3,打开放水闸门匀速放水,水池中的水量和放水时间的关系如表,下面说法不正确的是( )
放水时间(min)
1
2
3
4
…
水池中水量(m3)
48
46
44
42
…
A.放水时间是自变量,水池中的水量是因变量
B.每分钟放水2m3
C.放水25min后,水池中的水全部放完
D.放水10min后,水池中还有水28m3
二.填空题
11.“早穿皮袄,午穿纱,围着火炉吃西瓜.”这句谚语反映了我国新疆地区一天中,
随
变化而变化,其中自变量是
,因变量是
.
12.如图,圆柱的高是3cm,当圆柱的底面半径由小到大变化时,圆柱的体积也随之发生了变化.
(1)在这个变化中,自变量是
,因变量是
;
(2)当底面半径由1cm变化到10cm时,圆柱的体积增加了
cm3.
13.对于圆的周长公式c=2πr,其中自变量是
,因变量是
.
14.某汽车生产厂对其生产的A型汽车进行油耗试验,试验中汽车为匀速行驶,在行驶过程中,油箱的余油量y(升)与行驶时间t(小时)之间的关系如下表:
t(小时)
0
1
2
3
y(升)
100
92
84
76
由表格中y与t的关系可知,当汽车行驶
小时,油箱的余油量为40升.
15.已知点(﹣2,y1),(2,y2)都在直线y=2x﹣3上,则y1
y2.(填“<”或“>”或“=”)
16.如图,是体检时的心电图,其中横坐标x表示时间,纵坐标y表示心脏部位的生物电流,它们是两个变量.在心电图中,y
(填“是”或“不是”)x的函数.
17.夏季高山上温度从山脚起每升高100米降低0.7℃,已知山脚下温度是23℃,则温度y(℃)与上升高度x(米)之间关系式为
.
18.函数y=的自变量x的取值范围是
.
19.已知函数y=(m﹣1)x|m|+3是一次函数,则m=
.
20.按如图所示的程序计算函数y的值,若输入的x值为﹣3,则输出y的结果为
.
三.解答题
21.如图是一位病人的体温记录图,看图回答下列问题:
(1)自变量是
,因变量是
;
(2)护士每隔
小时给病人量一次体温;
(3)这位病人的最高体温是
摄氏度,最低体温是
摄氏度;
(4)他在4月8日12时的体温是
摄氏度;
(5)图中的横虚线表示
;
22.在函数y=中,求自变量x的取值范围.
23.已知y是x的函数,如表是y与x的几组对应值.
x
…
﹣5
﹣4
﹣3
﹣2
0
1
2
3
4
5
…
y
…
1.969
1.938
1.875
1.75
1
0
﹣2
﹣1.5
0
2.5
…
小明根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.
下面是小明的探究过程,请补充完整:
(1)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(2)根据画出的函数图象,写出:
①x=﹣1对应的函数值y约为
;
②该函数的一条性质:
.
24.写出下列各问题中的关系式中的常量与变量:
(1)分针旋转一周内,旋转的角度n(度)与旋转所需要的时间t(分)之间的关系式n=6t;
(2)一辆汽车以40千米/时的速度向前匀速直线行驶时,汽车行驶的路程S(千米)与行驶时间t(时)之间的关系式s=40t.
25.希望中学学生从2014年12月份开始每周喝营养牛奶,单价为2元/盒,总价y元随营养牛奶盒数x变化.指出其中的常量与变量,自变量与函数,并写出表示函数与自变量关系的式子.
26.阅读下面的材料:
如果函数y=f(x)满足:对于自变量x的取值范围内的任意x1,x2,
(1)若x1<x2,都有f(x1)<f(x2),则称f(x)是增函数;
(2)若x1<x2,都有f(x1)>f(x2),则称f(x)是减函数.
例题:证明函数f(x)=(x>0)是减函数.
证明:设0<x1<x2,
f(x1)﹣f(x2)=﹣==.
∵0<x1<x2,
∴x2﹣x1>0,x1x2>0.
∴>0.即f(x1)﹣f(x2)>0.
∴f(x1)>f(x2).
∴函数f(x)=(x>0)是减函数.
根据以上材料,解答下面的问题:
已知函数f(x)=+2x(x<0),
f(﹣1)=+(﹣2)=﹣1,f(﹣2)=+(﹣4)=﹣
(1)计算:f(﹣3)=
,f(﹣4)=
;
(2)猜想:函数f(x)=+2x(x<0)是
函数(填“增”或“减”);
(3)请仿照例题证明你的猜想.
27.有研究表明,声音在空气中的传播速度与空气的温度有关,当空气的温度变化,声音的传播速度也将随着变化.声音在空气中传播速度与空气温度关系一些数据(如下表格)
温度/℃
…
﹣20
﹣10
0
10
20
30
…
声速/(m/s)
…
318
324
330
336
342
348
…
(1)指出在这个变化过程中的自变量和因变量;
(2)当声音在空气中传播速度为342m/s时,此时空气的温度是多少?
(3)该数据表明:空气的温度每升高10℃,声音的传播速度将增大(或减少)多少?
(4)用y表示声音在空气中的传播速度,x表示空气温度,根据(3)中你发现的规律,直接写出y与x之间的关系式.
参考答案与试题解析
一.选择题
1.解:圆的周长计算公式是c=2πr,C和r是变量,2、π是常量,
故选:B.
2.解:∵篱笆的总长为60米,
∴周长p是定值,而面积S和一边长a是变量,
故选:B.
3.解:A、不能表示y是x的函数,故此选项不合题意;
B、不能表示y是x的函数,故此选项不合题意;
C、不能表示y是x的函数,故此选项不合题意;
D、能表示y是x的函数,故此选项符合题意;
故选:D.
4.解:根据题意可得:y=100×0.05x,
即y=5x.
故选:B.
5.解:由题意得,x﹣2≥0,
解得x≥2.
故选:B.
6.解:根据一次函数的性质,依次分析可得,
A、x=﹣2时,y=﹣2×﹣2+1=5,故图象必经过(﹣2,5),故错误,
B、k<0,则y随x的增大而减小,故错误,
C、k=﹣2<0,b=1>0,则图象经过第一、二、四象限,故错误,
D、当x>时,y<0,正确;
故选:D.
7.解:当y=0时,
方程x2+x+2=0无实数根,因此选项A不符合题意;
方程+1=0无实数根,因此选项B不符合题意;
方程x+=0无实数根,因此选项C不符合题意;
方程|x|﹣1=0的解为x=±1,因此选项D符合题意,
故选:D.
8.解:∵一次函数y=(m﹣2)xn﹣1+3是关于x的一次函数,
∴n﹣1=1且m﹣2≠0,
解得:n=2且m≠2.
故选:A.
9.解:∵汽车匀速行驶在高速公路上,速度是常量,随着时间的变化,行驶时间,行驶路程,剩余油量随之变化,
∴②行驶时间;③行驶路程;④汽车油箱中的剩余油量是变量.
故选:C.
10.解:根据表格数据知:蓄水池原有水50m3,每分钟水闸排水2m3.
水池剩余水量可以看以时间为自变量的函数故A正确.
∵每分钟水闸排水2m3.故B正确.
∵2×25=50.故C正确
放水10分钟,还剩水:50﹣2×10=30(m3).
故D错误.
故选:D.
二.填空题
11.解:“早穿皮袄,午穿纱,围着火炉吃西瓜.”这句谚语反映了我国新疆地区一天中,温度随时间变化而变化,其中自变量是:时间,因变量是:温度.
故答案是:温度、时间、时间、温度.
12.解:(1)根据函数的定义可知,对于底面半径的每个值,体积按照一定的法则有一个确定的值与之对应,所以自变量是:半径,因变量是:体积.
(2)体积增加了(π×102﹣π×12)×3=297πcm3.
故答案为:(1)半径,体积;(2)297π.
13.解:自变量是r,因变量是c.
14.解:由题意可得:y=100﹣8t,
当y=40时,40=100﹣8t
解得:t=7.5.
故答案为:7.5.
15.解:∵k=2>0,
∴y随x的增大而增大,
又∵﹣2<2,
∴y1<y2.
故答案为:<.
16.解:∵两个变量x和y,变量y随x的变化而变化,
且对于每一个x,y都有唯一值与之对应,
∴y是x的函数.
故答案为:是.
17.解:每升高100m降低0.7℃,则每上升1m,降低0.007℃,
则关系式为:y=23﹣0.007x;
故答案为:y=23﹣0.007x.
18.解:根据题意得,x﹣1≥0,
解得x≥1.
故答案为x≥1.
19.解:一次函数y=kx+b的定义条件是:k、b为常数,k≠0,自变量次数为1.
则得到|m|=1,m=±1,
∵m﹣1≠0,
∴m≠1,m=﹣1.
20.解:∵﹣3<﹣1,
把x=﹣3代入y=2x2,得y=2×9=18,
故答案为:18.
三.解答题
21.解:(1)自变量是时间,因变量是体温;
(2)护士每隔6小时给病人量一次体温;
(3)这位病人的最高体温是39.5摄氏度,最低体温是36.8摄氏度;
(4)他在4月8日12时的体温是37.5摄氏度;
(5)图中的横虚线表示人的正常体温;
故答案为:时间;体温;6;39.5;36.8;37.5;人的正常体温.
22.解:根据题意得:,
解得:﹣2≤x≤0或6≤x≤8.
故自变量x的取值范围是﹣2≤x≤0或6≤x≤8.
23.解:(1)如右图所求;
(2)①x=﹣1对应的函数值y约为1.5;
②当x<2时,y随x的增大而减小,(答案不唯一);
故答案为:1.5,当x<2时,y随x的增大而减小.
24.解:(1)常量:6;变量:n,t.
(2)常量:40;变量:s,t.
25.解:由题意得:
y=2x,
常量是2,变量是x、y,
x是自变量,y是x的函数.
26.解:(1)∵f(x)=+2x(x<0),
∴f(﹣3)=+2×(﹣3)=﹣,f(﹣4)=+2×(﹣4)=﹣
故答案为:﹣,﹣;
(2)∵﹣4<﹣3,f(﹣4)<f(﹣3)
∴函数f(x)=+2x(x<0)是增函数,
故答案为:增;
(3)设x1<x2<0,
∵f(x1)﹣f(x2)=+2x1﹣﹣2x2=(x1﹣x2)(2﹣)
∵x1<x2<0,
∴x1﹣x2<0,x1+x2<0,
∴f(x1)﹣f(x2)<0
∴f(x1)<f(x2)
∴函数f(x)=+2x(x<0)是增函数.
27.解:(1)自变量是温度,因变量是声速;
(2)由图表中数据可得出,当声音在空气中传播速度为342m/s时,此时空气的温度是20℃;
(3)利用表格中数据得出;空气的温度每升高10℃,声音的传播速度将增大6m/s;
(4)由图表中数据可得出:y=0.6x+330.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
