2021-2022学年苏科版八年级数学上册 第1章全等三角形 能力达标测评(word版含解析)
文档属性
| 名称 | 2021-2022学年苏科版八年级数学上册 第1章全等三角形 能力达标测评(word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 276.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-22 18:02:34 | ||
图片预览


文档简介
2021-2022学年苏科版八年级数学上册《第1章全等三角形》优生能力达标测评(附答案)
一.选择题(共10小题,每小题3分,共计30分)
1.在△ABC和△DEF中,∠A=∠D,AB=DE,则添加下列条件不能使△ABC≌△DEF成立的是( )
A.∠B=∠E
B.∠C=∠F
C.AC=DF
D.BC=EF
2.如图△ABC≌△DEF,B、E、C、F在同一直线上,BC=7,EC=4,则CF的长是( )
A.2
B.3
C.5
D.7
3.在△ABC中,∠A=60°,∠B=50°,AB=8,下列条件能得到△ABC≌△DEF的是( )
A.∠D=60°,∠E=50°,DF=8
B.∠D=60°,∠F=50°,DE=8
C.∠E=50°,∠F=70°,DE=8
D.∠D=60°,∠F=70°,EF=8
4.若△ABC≌△DEF,则根据图中提供的信息,可得出x的值为( )
A.30
B.27
C.35
D.40
5.如图△ACB≌△A′CB′,∠ACB=70°,∠ACB′=100°,则∠BCA′的度数为( )
A.30°
B.35°
C.40°
D.50°
6.如图,D为△ABC边BC上一点,AB=AC,∠BAC=56°,且BF=DC,EC=BD,则∠EDF等于( )
A.62°
B.56°
C.34°
D.124°
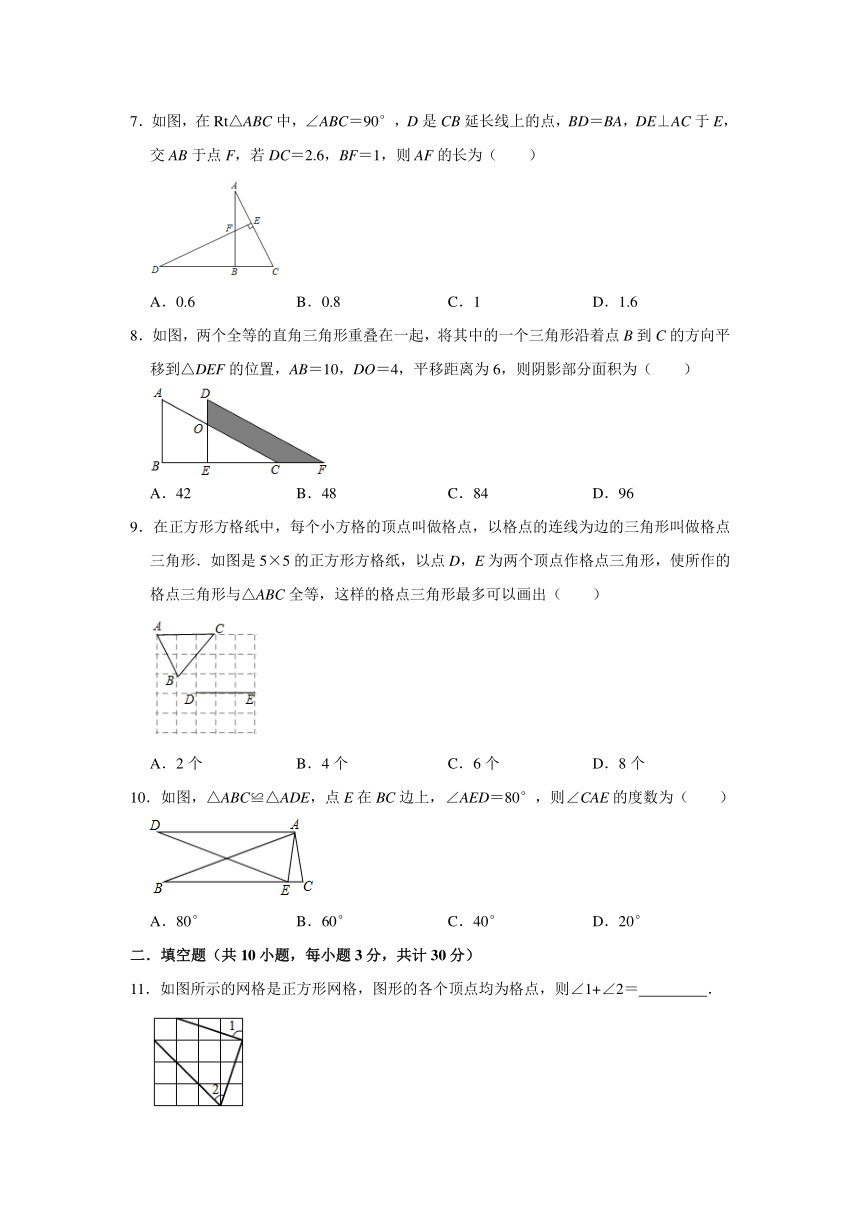
7.如图,在Rt△ABC中,∠ABC=90°,D是CB延长线上的点,BD=BA,DE⊥AC于E,交AB于点F,若DC=2.6,BF=1,则AF的长为( )
A.0.6
B.0.8
C.1
D.1.6
8.如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为( )
A.42
B.48
C.84
D.96
9.在正方形方格纸中,每个小方格的顶点叫做格点,以格点的连线为边的三角形叫做格点三角形.如图是5×5的正方形方格纸,以点D,E为两个顶点作格点三角形,使所作的格点三角形与△ABC全等,这样的格点三角形最多可以画出( )
A.2个
B.4个
C.6个
D.8个
10.如图,△ABC≌△ADE,点E在BC边上,∠AED=80°,则∠CAE的度数为( )
A.80°
B.60°
C.40°
D.20°
二.填空题(共10小题,每小题3分,共计30分)
11.如图所示的网格是正方形网格,图形的各个顶点均为格点,则∠1+∠2=
.
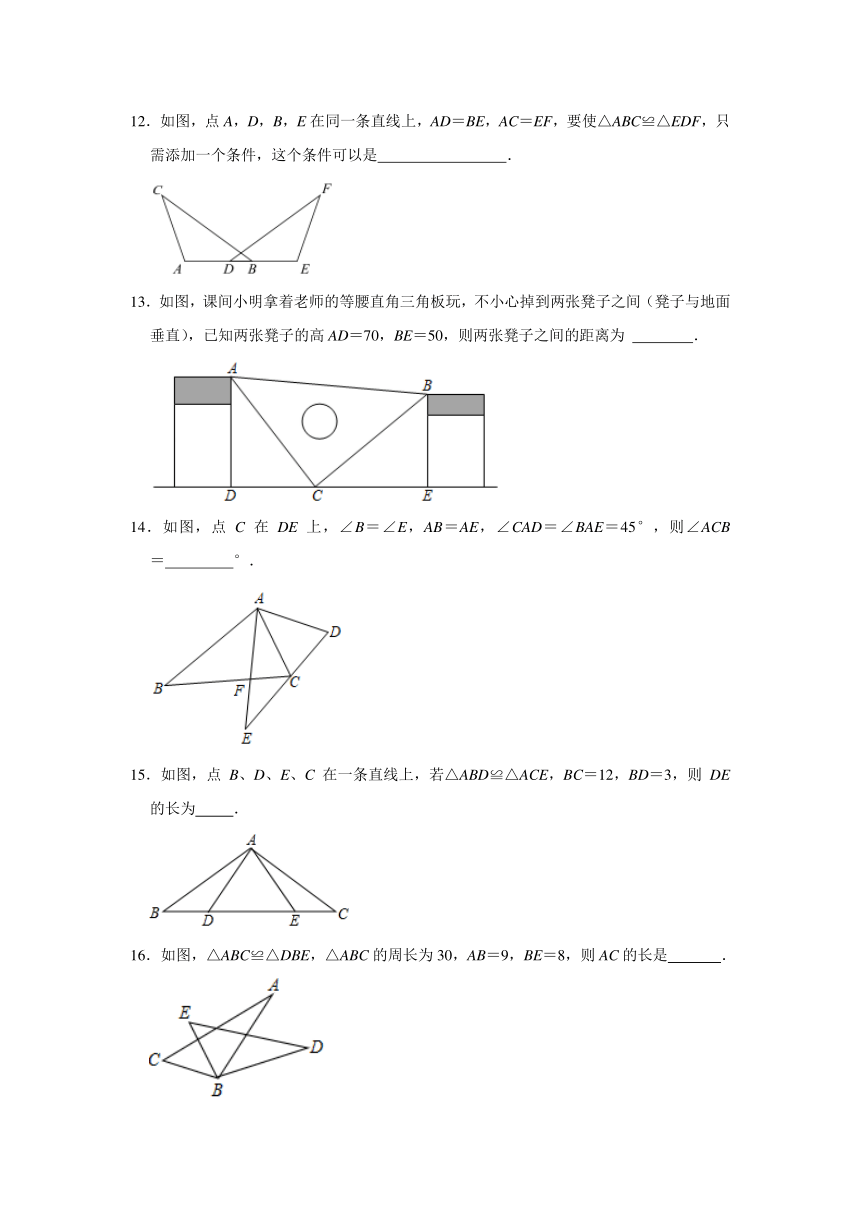
12.如图,点A,D,B,E在同一条直线上,AD=BE,AC=EF,要使△ABC≌△EDF,只需添加一个条件,这个条件可以是
.
13.如图,课间小明拿着老师的等腰直角三角板玩,不小心掉到两张凳子之间(凳子与地面垂直),已知两张凳子的高AD=70,BE=50,则两张凳子之间的距离为
.
14.如图,点C在DE上,∠B=∠E,AB=AE,∠CAD=∠BAE=45°,则∠ACB=
°.
15.如图,点
B、D、E、C在一条直线上,若△ABD≌△ACE,BC=12,BD=3,则DE的长为
.
16.如图,△ABC≌△DBE,△ABC的周长为30,AB=9,BE=8,则AC的长是
.
17.如图,AB=12m,CA⊥AB于A,DB⊥AB于B,且AC=4m,P点从B向A运动,每分钟走1m,Q点从B向D运动,每分钟走2m,P、Q两点同时出发,运动
分钟后,△CAP与△PQB全等.
18.如图,△ABC中,AB=AC,点D、E、F分别在AB、BC、CA边上,且BE=CF,BD=CE,如果∠A=44°,则∠EDF的度数为
.
19.已知△ABC≌△DEF,BC=EF=10cm,若△DEF的面积是40cm2,则△ABC中BC边上的高是
cm.
20.如图,AB=4cm,AC=BD=3cm.∠CAB=∠DBA,点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.设运动时间为t(s),则当点Q的运动速度为
cm/s时,△ACP与△BPQ全等.
三.解答题(共10小题,每小题6分,共计60分)
21.如图,点E、F在AB上,且AE=BF,DE=CF,CF∥DE.
求证:AC∥BD.
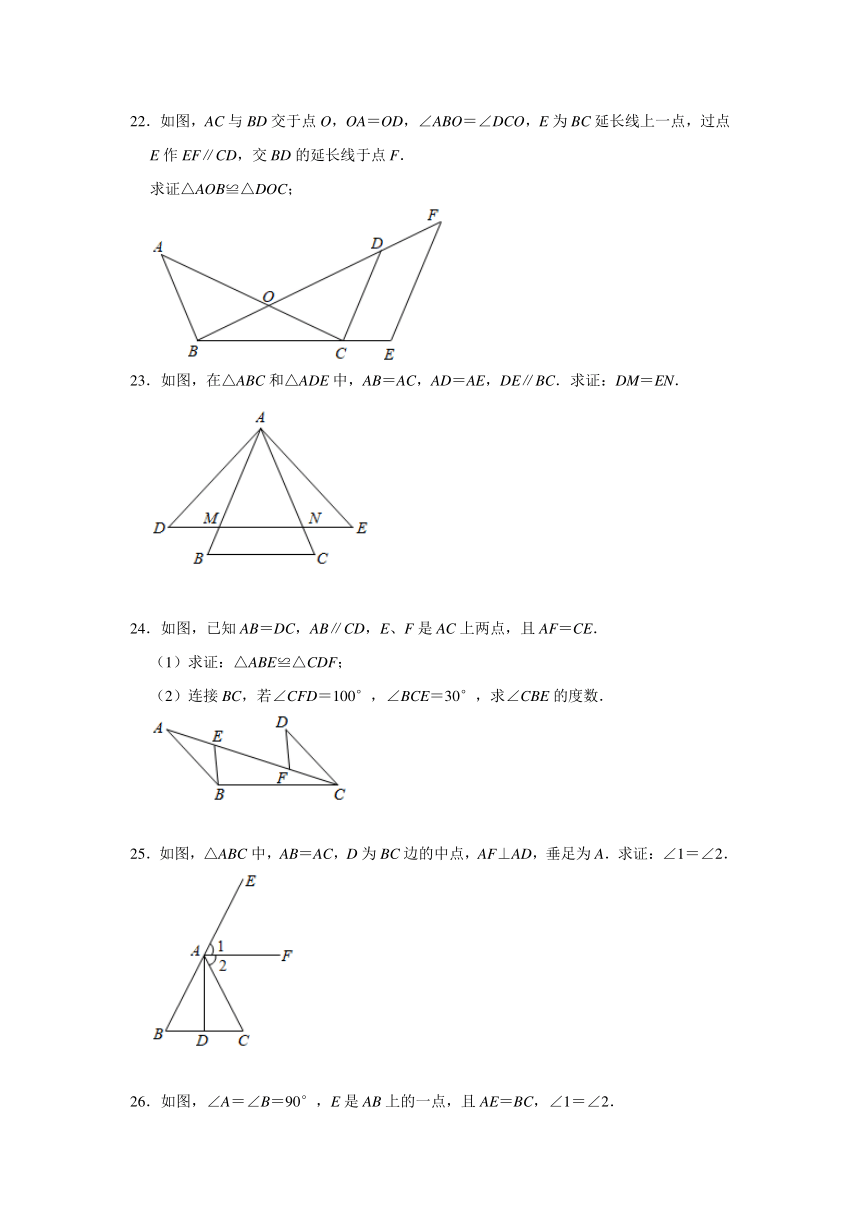
22.如图,AC与BD交于点O,OA=OD,∠ABO=∠DCO,E为BC延长线上一点,过点E作EF∥CD,交BD的延长线于点F.
求证△AOB≌△DOC;
23.如图,在△ABC和△ADE中,AB=AC,AD=AE,DE∥BC.求证:DM=EN.
24.如图,已知AB=DC,AB∥CD,E、F是AC上两点,且AF=CE.
(1)求证:△ABE≌△CDF;
(2)连接BC,若∠CFD=100°,∠BCE=30°,求∠CBE的度数.
25.如图,△ABC中,AB=AC,D为BC边的中点,AF⊥AD,垂足为A.求证:∠1=∠2.
26.如图,∠A=∠B=90°,E是AB上的一点,且AE=BC,∠1=∠2.
(1)求证:△ADE≌△BEC;
(2)若M是线段DC的中点,连接EM,请写出线段EM与AD、BC之间的数量关系,并说明理由.
27.如图,点
C、E、F、B在同一直线上,CE=BF,AB=CD,AB∥CD.
(1)求证∠A=∠D;
(2)若AB=BE,∠B=40°,求∠D的度数.
28.如图,在Rt△ABC和Rt△DEF中,∠C=∠F=90°,点
A、E、B、D在同一直线上,BC、EF交于点M,AC=DF,AB=DE.
求证:(1)∠CBA=∠FED;
(2)AM=DM.
29.如图,四边形ABCD的对角线AC、BD相交于点O,OA=OB,OC=OD.求证:
(1)AB∥CD;
(2)△ABC≌△BAD.
30.在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,猜想线段DE、AD与BE有怎样的数量关系?请写出这个关系(不用证明);
(2)当直线MN绕点C旋转到图2的位置时,求证:DE=AD﹣BE;
(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明.
参考答案
一.选择题(共10小题,每小题3分,共计30分)
1.解:A、添加∠B=∠E,可利用AAS定理判定△ABC≌△DEF,故此选项不合题意;
B、添加∠C=∠F,可利用AAS定理判定△ABC≌△DEF,故此选项不合题意;
C、添加AC=DF,可利用SAS定理判定△ABC≌△DEF,故此选项不合题意;
D、添加BC=EF,不能判定△ABC≌△DEF,故此选项符合题意;
故选:D.
2.解:∵△ABC≌△DEF,BC=7,
∴EF=BC=7,
∴CF=EF﹣EC=3,
故选:B.
3.解:∵△ABC≌△DEF,
∴∠B=∠E=50°,∠A=∠D=60°,AB=DE=8,
∴∠F=180°﹣∠E﹣∠D=70°,
故选:C.
4.解:∵△ABC≌△DEF,
∴BC=EF=30,
故选:A.
5.解:∵△ACB≌△A′CB′,
∴∠A′CB′=∠ACB=70°,
∵∠ACB′=100°,
∴∠BCB′=∠ACB′﹣∠ACB=30°,
∴∠BCA′=∠A′CB′﹣∠BCB′=40°,
故选:C.
6.解:∵AB=AC,
∴∠B=∠C=(180°﹣∠BAC)=(180°﹣56°)=62°,
在△BFD和△EDC中,,
∴△BFD≌△EDC(SAS),
∴∠BFD=∠EDC,
∴∠FDB+∠EDC=∠FDB+∠BFD=180°﹣∠B=180°﹣62°=118°,
则∠EDF=180°﹣(∠FDB+∠EDC)=180°﹣118°=62°.
故选:A.
7.解:∵DE⊥AC于E,
∴∠FDB+∠C=90°,
∵∠ABC=90°,
∴∠D+∠DFB=90°,
∴∠C=∠BFD,
在△DBF与△ABC中,
,
∴△DBF≌△ABC(AAS),
∴BF=BC,
∵DC=2.6,BF=1,
∴AF=AB﹣BF=BD﹣BF=DC﹣BF﹣BF=2.6﹣1﹣1=0.6,
故选:A.
8.解:由平移的性质知,BE=6,DE=AB=10,
∴OE=DE﹣DO=10﹣4=6,
∵△ABC≌△DEF,
∴S△ABC=S△DEF,
∴S四边形ODFC=S梯形ABEO=(AB+OE)?BE=(10+6)×6=48,
故选:B.
9.解:根据题意,运用SSS可得与△ABC全等的三角形有4个,线段DE的上方有两个点,下方也有两个点.
故选:B.
10.解:∵△ABC≌△ADE,∠AED=80°,
∴∠C=∠AED=80°,AE=AC,
∴∠AEC=∠C=80°,
∴∠CAE=180°﹣∠C﹣∠AEC=180°﹣80°﹣80°=20°,
故选:D.
二.填空题(共10小题,每小题3分,共计30分)
11.解:如图所示:
由题意可得:∠1=∠3,
则∠1+∠2=∠2+∠3=135°.
故答案为:135°.
12.解:添加BC=DF.
∵AD=BE,
∴AD+DB=BE+BD,
∴AB=ED,
在△ABC和△EDF中,
,
∴△ABC≌△EDF(SSS),
故答案为:BC=DF(答案不唯一).
13.解:由题意可得:∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,
则∠DAC=∠BCE,
在△ACD和△CBE中,
,
∴△ACD≌△CBE(AAS),
∴DC=BE=50,AD=CE=70,
则两张凳子之间的距离为:50+70=120.
故答案为:120.
14.解:∵∠CAD=∠BAE=45°,
∴∠BAC=∠DAE,
在△ABC和△AED中,
,
∴△ABC≌△EAD(ASA),
∴AD=AC,∠ACB=∠D,
∴∠D=∠ACD=67.5°,
∴∠ACB=67.5°,
故答案为67.5.
15.解:∵△ABD≌△ACE,BD=3,
∴BD=CE=3,
∵BC=12,
∴DE=BC﹣BD﹣CE=12﹣3﹣3=6.
故答案为:6.
16.解:∵△ABC≌△DBE,BE=8,
∴BC=BE=8,
∵△ABC的周长为30,
∴AB+AC+BC=30,
∴AC=30﹣AB﹣BC=13,
故答案为:13.
17.解:∵CA⊥AB于A,DB⊥AB于B,
∴∠A=∠B=90°,
设运动x分钟后△CAP与△PQB全等;
则BP=xm,BQ=2xm,则AP=(12﹣x)m,
分两种情况:
①若BP=AC,则x=4,
AP=12﹣4=8,BQ=8,AP=BQ,
∴△CAP≌△PBQ;
②若BP=AP,则12﹣x=x,
解得:x=6,BQ=12≠AC,
此时△CAP与△PQB不全等;
综上所述:运动4分钟后△CAP与△PQB全等;
故答案为:4.
18.解:∵AB=AC,
∴∠ABC=∠ACB,
在△DBE和△ECF中
,
∴△DBE≌△ECF(SAS),
∴DE=EF,
∴△DEF是等腰三角形;
∵△DBE≌△ECF,
∴∠1=∠3,∠2=∠4,
∵∠A+∠B+∠C=180°,
∴∠B=(180°﹣44°)=68°
∴∠1+∠2=180°﹣68°
∴∠3+∠2=180°﹣68°
∴∠DEF=68°,
∴∠EDF=.
故答案为:56°.
19.解:设△DEF中BC边上的高是hcm,
由题意得,×10×h=40,
解得,h=8,
∵△ABC≌△DEF,
∴△ABC中BC边上的高=△DEF中BC边上的高=8cm,
故答案为:8.
20.解:设点Q的运动速度是xcm/s,
∵∠CAB=∠DBA,
∴△ACP与△BPQ全等,有两种情况:
①AP=BP,AC=BQ,
则1×t=4﹣1×t,
解得:t=2,
则3=2x,
解得:x=1.5;
②AP=BQ,AC=BP,
则1×t=tx,4﹣1×t=3,
解得:t=1,x=1,
故答案为:1或1.5.
三.解答题(共10小题,每小题6分,共计60分)
21.证明:∵AE=BF,
∴AE+EF=BF+EF,
即AF=BE,
∵CF∥DE.
∴∠AFC=∠BED,
在△ACF和△BDE中,
∴△ACF≌△BDE(SAS),
∴∠A=∠B,
∴AC∥BD.
22.(1)证明:在△AOB和△DOC中,
,
∴△AOB≌△DOC(AAS);
23.证明:∵AB=AC,AD=AE,
∴∠B=∠C,∠D=∠E,
∵DE∥BC,
∴∠AMN=∠B,∠C=∠ANM,
∴∠AMN=∠ANM,
在△ADN和△AEM中,
,
∴△ADN≌△AEM(AAS),
∴DN=EM,
∴DM=NE.
24.(1)证明:∵AB∥CD,
∴∠A=∠DCF,
∵AF=CE,
∴AE=CF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS).
(2)∵△ABE≌△CDF,
∴∠AEB=∠CFD=100°,
∴∠BEC=180°﹣100°=80°,
∴∠CBE=180°﹣80°﹣30°=70°.
25.证明:∵AB=AC,D为BC边的中点,
∴AD⊥BC,
∵AF⊥AD,
∴AF∥BC,
∴∠ACB=∠2,∠1=∠B,
∵AB=AC,
∴∠B=∠ACB,
∴∠1=∠2.
26.证明:(1)∵∠1=∠2,
∴ED=EC,
∵∠A=∠B=90°,
在Rt△ADE和Rt△BEC中,
,
∴Rt△ADE≌Rt△BEC(HL);
(2)AD2+BC2=2EM2,理由如下:
由(1)得Rt△ADE≌Rt△BEC,DE=CE,
∴∠AED=∠BCE,BC=AE,
∵∠A=∠B=90°,
∴∠BCE+∠CEB=90°,
∴∠AED+∠CEB=90°,
∴∠DEC=180°﹣90°=90°,
∵∠1=∠2,
∴△DEC为等腰直角三角形,
∵M为DC中点,
∴EM=DC,且EM⊥CD,
∴EM=DM,
在Rt△ADE中,DE2=AD2+AE2=AD2+BC2,
同理可得,在Rt△EMD中,DE2=EM2+DM2=2EM2,
∴AD2+BC2=2EM2.
27.(1)证明:∵AB∥CD,
∴∠C=∠B,
∵CE=BF,
∴CE+EF=FB+EF,
即CF=BE,
在△AEB和△DFC中,
,
∴△AEB≌△DFC(SAS),
∴∠A=∠D;
(2)解:∵AB=BE,
∴∠A=∠AEB,
∵∠B=40°,
∴∠A=∠AEB=×(180°﹣∠B)=×(180°﹣40°)=70°,
∴∠D=∠A=70°.
28.证明:(1)在Rt△ABC和Rt△DEF中,∠C=∠F=90°,
,
∴Rt△ABC≌Rt△DEF(HL),
∴∠CBA=∠FED;
(2)∵∠CBA=∠FED,
∴ME=MB,且∠AEM=∠DBM,
∵AB=DE,
∴AB﹣EB=DE﹣EB,
即AE=DB,
在△AEM和△DBM中,
,
∴△AEM≌△DBM(SAS),
∴AM=DM.
29.(1)证明:∵OA=OB,OC=OD,
∴∠OAB=∠OBA,∠OCD=∠ODC,
∵∠COD=∠AOB,∠OAB+∠OBA+∠AOB=180°,∠OCD+∠ODC+∠COD=180°,
∴∠OAB=∠OBA=∠OCD=∠ODC,
即∠OAB=∠OCD,
∴AB∥CD;
(2)∵OA=OB,OC=OD,
∴AC=BD,
在△ABC和△BAD中,
,
∴△ABC≌△BAD(SAS).
30.(1)解:DE=CD+CE=AD+BE.
(2)证明:∵∠ACB=90°,∴∠ACD+∠BCE=90°,
∵AD⊥DN,∴∠ACD+∠CAD=90°,
∴∠CAD=∠BCE,又AC=BC,
∴△ACD≌△CBE(AAS),∴AD=CE,BE=CD,
DE=CE﹣CD=AD﹣BE.
(3)解:DE=CD﹣CE=BE﹣AD.
证明:∵∠ACB=90°,∴∠ACD+∠BCE=90°,
∵AD⊥DN,∴∠ACD+∠CAD=90°,
∴∠CAD=∠BCE,又AC=BC,
∴△ACD≌△CBE(AAS),∴AD=CE,BE=CD,
DE=CD﹣CE=BE﹣AD.
一.选择题(共10小题,每小题3分,共计30分)
1.在△ABC和△DEF中,∠A=∠D,AB=DE,则添加下列条件不能使△ABC≌△DEF成立的是( )
A.∠B=∠E
B.∠C=∠F
C.AC=DF
D.BC=EF
2.如图△ABC≌△DEF,B、E、C、F在同一直线上,BC=7,EC=4,则CF的长是( )
A.2
B.3
C.5
D.7
3.在△ABC中,∠A=60°,∠B=50°,AB=8,下列条件能得到△ABC≌△DEF的是( )
A.∠D=60°,∠E=50°,DF=8
B.∠D=60°,∠F=50°,DE=8
C.∠E=50°,∠F=70°,DE=8
D.∠D=60°,∠F=70°,EF=8
4.若△ABC≌△DEF,则根据图中提供的信息,可得出x的值为( )
A.30
B.27
C.35
D.40
5.如图△ACB≌△A′CB′,∠ACB=70°,∠ACB′=100°,则∠BCA′的度数为( )
A.30°
B.35°
C.40°
D.50°
6.如图,D为△ABC边BC上一点,AB=AC,∠BAC=56°,且BF=DC,EC=BD,则∠EDF等于( )
A.62°
B.56°
C.34°
D.124°
7.如图,在Rt△ABC中,∠ABC=90°,D是CB延长线上的点,BD=BA,DE⊥AC于E,交AB于点F,若DC=2.6,BF=1,则AF的长为( )
A.0.6
B.0.8
C.1
D.1.6
8.如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为( )
A.42
B.48
C.84
D.96
9.在正方形方格纸中,每个小方格的顶点叫做格点,以格点的连线为边的三角形叫做格点三角形.如图是5×5的正方形方格纸,以点D,E为两个顶点作格点三角形,使所作的格点三角形与△ABC全等,这样的格点三角形最多可以画出( )
A.2个
B.4个
C.6个
D.8个
10.如图,△ABC≌△ADE,点E在BC边上,∠AED=80°,则∠CAE的度数为( )
A.80°
B.60°
C.40°
D.20°
二.填空题(共10小题,每小题3分,共计30分)
11.如图所示的网格是正方形网格,图形的各个顶点均为格点,则∠1+∠2=
.
12.如图,点A,D,B,E在同一条直线上,AD=BE,AC=EF,要使△ABC≌△EDF,只需添加一个条件,这个条件可以是
.
13.如图,课间小明拿着老师的等腰直角三角板玩,不小心掉到两张凳子之间(凳子与地面垂直),已知两张凳子的高AD=70,BE=50,则两张凳子之间的距离为
.
14.如图,点C在DE上,∠B=∠E,AB=AE,∠CAD=∠BAE=45°,则∠ACB=
°.
15.如图,点
B、D、E、C在一条直线上,若△ABD≌△ACE,BC=12,BD=3,则DE的长为
.
16.如图,△ABC≌△DBE,△ABC的周长为30,AB=9,BE=8,则AC的长是
.
17.如图,AB=12m,CA⊥AB于A,DB⊥AB于B,且AC=4m,P点从B向A运动,每分钟走1m,Q点从B向D运动,每分钟走2m,P、Q两点同时出发,运动
分钟后,△CAP与△PQB全等.
18.如图,△ABC中,AB=AC,点D、E、F分别在AB、BC、CA边上,且BE=CF,BD=CE,如果∠A=44°,则∠EDF的度数为
.
19.已知△ABC≌△DEF,BC=EF=10cm,若△DEF的面积是40cm2,则△ABC中BC边上的高是
cm.
20.如图,AB=4cm,AC=BD=3cm.∠CAB=∠DBA,点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.设运动时间为t(s),则当点Q的运动速度为
cm/s时,△ACP与△BPQ全等.
三.解答题(共10小题,每小题6分,共计60分)
21.如图,点E、F在AB上,且AE=BF,DE=CF,CF∥DE.
求证:AC∥BD.
22.如图,AC与BD交于点O,OA=OD,∠ABO=∠DCO,E为BC延长线上一点,过点E作EF∥CD,交BD的延长线于点F.
求证△AOB≌△DOC;
23.如图,在△ABC和△ADE中,AB=AC,AD=AE,DE∥BC.求证:DM=EN.
24.如图,已知AB=DC,AB∥CD,E、F是AC上两点,且AF=CE.
(1)求证:△ABE≌△CDF;
(2)连接BC,若∠CFD=100°,∠BCE=30°,求∠CBE的度数.
25.如图,△ABC中,AB=AC,D为BC边的中点,AF⊥AD,垂足为A.求证:∠1=∠2.
26.如图,∠A=∠B=90°,E是AB上的一点,且AE=BC,∠1=∠2.
(1)求证:△ADE≌△BEC;
(2)若M是线段DC的中点,连接EM,请写出线段EM与AD、BC之间的数量关系,并说明理由.
27.如图,点
C、E、F、B在同一直线上,CE=BF,AB=CD,AB∥CD.
(1)求证∠A=∠D;
(2)若AB=BE,∠B=40°,求∠D的度数.
28.如图,在Rt△ABC和Rt△DEF中,∠C=∠F=90°,点
A、E、B、D在同一直线上,BC、EF交于点M,AC=DF,AB=DE.
求证:(1)∠CBA=∠FED;
(2)AM=DM.
29.如图,四边形ABCD的对角线AC、BD相交于点O,OA=OB,OC=OD.求证:
(1)AB∥CD;
(2)△ABC≌△BAD.
30.在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图1的位置时,猜想线段DE、AD与BE有怎样的数量关系?请写出这个关系(不用证明);
(2)当直线MN绕点C旋转到图2的位置时,求证:DE=AD﹣BE;
(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明.
参考答案
一.选择题(共10小题,每小题3分,共计30分)
1.解:A、添加∠B=∠E,可利用AAS定理判定△ABC≌△DEF,故此选项不合题意;
B、添加∠C=∠F,可利用AAS定理判定△ABC≌△DEF,故此选项不合题意;
C、添加AC=DF,可利用SAS定理判定△ABC≌△DEF,故此选项不合题意;
D、添加BC=EF,不能判定△ABC≌△DEF,故此选项符合题意;
故选:D.
2.解:∵△ABC≌△DEF,BC=7,
∴EF=BC=7,
∴CF=EF﹣EC=3,
故选:B.
3.解:∵△ABC≌△DEF,
∴∠B=∠E=50°,∠A=∠D=60°,AB=DE=8,
∴∠F=180°﹣∠E﹣∠D=70°,
故选:C.
4.解:∵△ABC≌△DEF,
∴BC=EF=30,
故选:A.
5.解:∵△ACB≌△A′CB′,
∴∠A′CB′=∠ACB=70°,
∵∠ACB′=100°,
∴∠BCB′=∠ACB′﹣∠ACB=30°,
∴∠BCA′=∠A′CB′﹣∠BCB′=40°,
故选:C.
6.解:∵AB=AC,
∴∠B=∠C=(180°﹣∠BAC)=(180°﹣56°)=62°,
在△BFD和△EDC中,,
∴△BFD≌△EDC(SAS),
∴∠BFD=∠EDC,
∴∠FDB+∠EDC=∠FDB+∠BFD=180°﹣∠B=180°﹣62°=118°,
则∠EDF=180°﹣(∠FDB+∠EDC)=180°﹣118°=62°.
故选:A.
7.解:∵DE⊥AC于E,
∴∠FDB+∠C=90°,
∵∠ABC=90°,
∴∠D+∠DFB=90°,
∴∠C=∠BFD,
在△DBF与△ABC中,
,
∴△DBF≌△ABC(AAS),
∴BF=BC,
∵DC=2.6,BF=1,
∴AF=AB﹣BF=BD﹣BF=DC﹣BF﹣BF=2.6﹣1﹣1=0.6,
故选:A.
8.解:由平移的性质知,BE=6,DE=AB=10,
∴OE=DE﹣DO=10﹣4=6,
∵△ABC≌△DEF,
∴S△ABC=S△DEF,
∴S四边形ODFC=S梯形ABEO=(AB+OE)?BE=(10+6)×6=48,
故选:B.
9.解:根据题意,运用SSS可得与△ABC全等的三角形有4个,线段DE的上方有两个点,下方也有两个点.
故选:B.
10.解:∵△ABC≌△ADE,∠AED=80°,
∴∠C=∠AED=80°,AE=AC,
∴∠AEC=∠C=80°,
∴∠CAE=180°﹣∠C﹣∠AEC=180°﹣80°﹣80°=20°,
故选:D.
二.填空题(共10小题,每小题3分,共计30分)
11.解:如图所示:
由题意可得:∠1=∠3,
则∠1+∠2=∠2+∠3=135°.
故答案为:135°.
12.解:添加BC=DF.
∵AD=BE,
∴AD+DB=BE+BD,
∴AB=ED,
在△ABC和△EDF中,
,
∴△ABC≌△EDF(SSS),
故答案为:BC=DF(答案不唯一).
13.解:由题意可得:∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,
则∠DAC=∠BCE,
在△ACD和△CBE中,
,
∴△ACD≌△CBE(AAS),
∴DC=BE=50,AD=CE=70,
则两张凳子之间的距离为:50+70=120.
故答案为:120.
14.解:∵∠CAD=∠BAE=45°,
∴∠BAC=∠DAE,
在△ABC和△AED中,
,
∴△ABC≌△EAD(ASA),
∴AD=AC,∠ACB=∠D,
∴∠D=∠ACD=67.5°,
∴∠ACB=67.5°,
故答案为67.5.
15.解:∵△ABD≌△ACE,BD=3,
∴BD=CE=3,
∵BC=12,
∴DE=BC﹣BD﹣CE=12﹣3﹣3=6.
故答案为:6.
16.解:∵△ABC≌△DBE,BE=8,
∴BC=BE=8,
∵△ABC的周长为30,
∴AB+AC+BC=30,
∴AC=30﹣AB﹣BC=13,
故答案为:13.
17.解:∵CA⊥AB于A,DB⊥AB于B,
∴∠A=∠B=90°,
设运动x分钟后△CAP与△PQB全等;
则BP=xm,BQ=2xm,则AP=(12﹣x)m,
分两种情况:
①若BP=AC,则x=4,
AP=12﹣4=8,BQ=8,AP=BQ,
∴△CAP≌△PBQ;
②若BP=AP,则12﹣x=x,
解得:x=6,BQ=12≠AC,
此时△CAP与△PQB不全等;
综上所述:运动4分钟后△CAP与△PQB全等;
故答案为:4.
18.解:∵AB=AC,
∴∠ABC=∠ACB,
在△DBE和△ECF中
,
∴△DBE≌△ECF(SAS),
∴DE=EF,
∴△DEF是等腰三角形;
∵△DBE≌△ECF,
∴∠1=∠3,∠2=∠4,
∵∠A+∠B+∠C=180°,
∴∠B=(180°﹣44°)=68°
∴∠1+∠2=180°﹣68°
∴∠3+∠2=180°﹣68°
∴∠DEF=68°,
∴∠EDF=.
故答案为:56°.
19.解:设△DEF中BC边上的高是hcm,
由题意得,×10×h=40,
解得,h=8,
∵△ABC≌△DEF,
∴△ABC中BC边上的高=△DEF中BC边上的高=8cm,
故答案为:8.
20.解:设点Q的运动速度是xcm/s,
∵∠CAB=∠DBA,
∴△ACP与△BPQ全等,有两种情况:
①AP=BP,AC=BQ,
则1×t=4﹣1×t,
解得:t=2,
则3=2x,
解得:x=1.5;
②AP=BQ,AC=BP,
则1×t=tx,4﹣1×t=3,
解得:t=1,x=1,
故答案为:1或1.5.
三.解答题(共10小题,每小题6分,共计60分)
21.证明:∵AE=BF,
∴AE+EF=BF+EF,
即AF=BE,
∵CF∥DE.
∴∠AFC=∠BED,
在△ACF和△BDE中,
∴△ACF≌△BDE(SAS),
∴∠A=∠B,
∴AC∥BD.
22.(1)证明:在△AOB和△DOC中,
,
∴△AOB≌△DOC(AAS);
23.证明:∵AB=AC,AD=AE,
∴∠B=∠C,∠D=∠E,
∵DE∥BC,
∴∠AMN=∠B,∠C=∠ANM,
∴∠AMN=∠ANM,
在△ADN和△AEM中,
,
∴△ADN≌△AEM(AAS),
∴DN=EM,
∴DM=NE.
24.(1)证明:∵AB∥CD,
∴∠A=∠DCF,
∵AF=CE,
∴AE=CF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS).
(2)∵△ABE≌△CDF,
∴∠AEB=∠CFD=100°,
∴∠BEC=180°﹣100°=80°,
∴∠CBE=180°﹣80°﹣30°=70°.
25.证明:∵AB=AC,D为BC边的中点,
∴AD⊥BC,
∵AF⊥AD,
∴AF∥BC,
∴∠ACB=∠2,∠1=∠B,
∵AB=AC,
∴∠B=∠ACB,
∴∠1=∠2.
26.证明:(1)∵∠1=∠2,
∴ED=EC,
∵∠A=∠B=90°,
在Rt△ADE和Rt△BEC中,
,
∴Rt△ADE≌Rt△BEC(HL);
(2)AD2+BC2=2EM2,理由如下:
由(1)得Rt△ADE≌Rt△BEC,DE=CE,
∴∠AED=∠BCE,BC=AE,
∵∠A=∠B=90°,
∴∠BCE+∠CEB=90°,
∴∠AED+∠CEB=90°,
∴∠DEC=180°﹣90°=90°,
∵∠1=∠2,
∴△DEC为等腰直角三角形,
∵M为DC中点,
∴EM=DC,且EM⊥CD,
∴EM=DM,
在Rt△ADE中,DE2=AD2+AE2=AD2+BC2,
同理可得,在Rt△EMD中,DE2=EM2+DM2=2EM2,
∴AD2+BC2=2EM2.
27.(1)证明:∵AB∥CD,
∴∠C=∠B,
∵CE=BF,
∴CE+EF=FB+EF,
即CF=BE,
在△AEB和△DFC中,
,
∴△AEB≌△DFC(SAS),
∴∠A=∠D;
(2)解:∵AB=BE,
∴∠A=∠AEB,
∵∠B=40°,
∴∠A=∠AEB=×(180°﹣∠B)=×(180°﹣40°)=70°,
∴∠D=∠A=70°.
28.证明:(1)在Rt△ABC和Rt△DEF中,∠C=∠F=90°,
,
∴Rt△ABC≌Rt△DEF(HL),
∴∠CBA=∠FED;
(2)∵∠CBA=∠FED,
∴ME=MB,且∠AEM=∠DBM,
∵AB=DE,
∴AB﹣EB=DE﹣EB,
即AE=DB,
在△AEM和△DBM中,
,
∴△AEM≌△DBM(SAS),
∴AM=DM.
29.(1)证明:∵OA=OB,OC=OD,
∴∠OAB=∠OBA,∠OCD=∠ODC,
∵∠COD=∠AOB,∠OAB+∠OBA+∠AOB=180°,∠OCD+∠ODC+∠COD=180°,
∴∠OAB=∠OBA=∠OCD=∠ODC,
即∠OAB=∠OCD,
∴AB∥CD;
(2)∵OA=OB,OC=OD,
∴AC=BD,
在△ABC和△BAD中,
,
∴△ABC≌△BAD(SAS).
30.(1)解:DE=CD+CE=AD+BE.
(2)证明:∵∠ACB=90°,∴∠ACD+∠BCE=90°,
∵AD⊥DN,∴∠ACD+∠CAD=90°,
∴∠CAD=∠BCE,又AC=BC,
∴△ACD≌△CBE(AAS),∴AD=CE,BE=CD,
DE=CE﹣CD=AD﹣BE.
(3)解:DE=CD﹣CE=BE﹣AD.
证明:∵∠ACB=90°,∴∠ACD+∠BCE=90°,
∵AD⊥DN,∴∠ACD+∠CAD=90°,
∴∠CAD=∠BCE,又AC=BC,
∴△ACD≌△CBE(AAS),∴AD=CE,BE=CD,
DE=CD﹣CE=BE﹣AD.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
