2021-2022学年苏科版九年级数学上册 2.6正多边形与圆 同步提升训练(word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版九年级数学上册 2.6正多边形与圆 同步提升训练(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 391.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-22 18:31:19 | ||
图片预览

文档简介
2021-2022学年苏科版九年级数学上册《2.6正多边形与圆》同步能力提升训练(附答案)
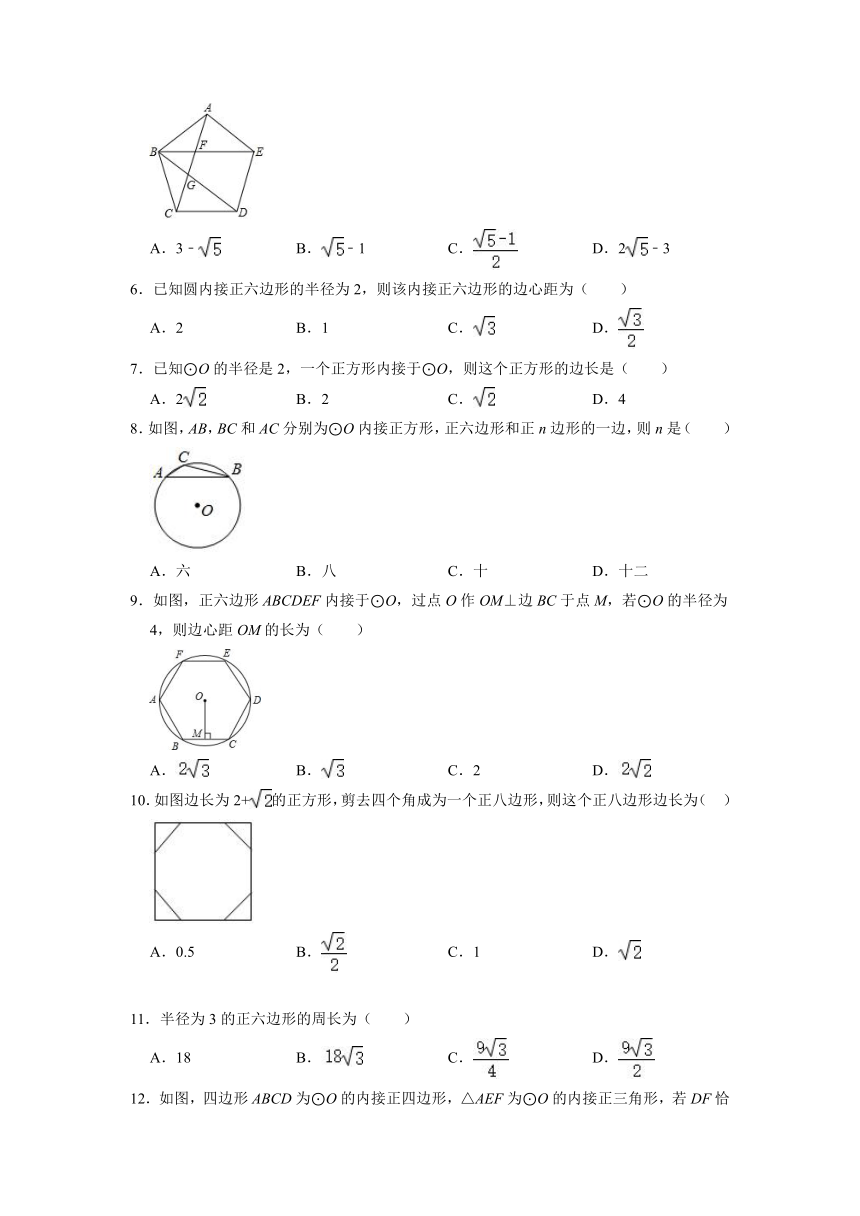
1.如图,⊙O是正六边形ABCDEF的外接圆,点P在⊙O上(P不与A,B重合),则∠APB的度数为( )
A.30°或150°
B.60°或120°
C.30°
D.60°
2.如图,点O为正六边形的中心,P、Q分别从点A(﹣1,0)同时出发,沿正六边形按图示方向运动,点P的速度为每秒1个单位长度,点Q的速度为每秒2个单位长度,则第2021次相遇地点的坐标为( )
A.
B.(1,0)
C.
D.(﹣1,0)
3.如图,正方形ABCD内接于⊙O.点E为上一点,连接BE、CE,若∠CBE=15°,BE=3,则BC的长为( )
A.
B.
C.
D.
4.如图,已知正六边形ABCDEF的边长为1,分别以其对角线AD、CE为边作正方形,则两个阴影部分的面积差a﹣b的值为( )
A.0
B.2
C.1
D.
5.如图,在正五边形ABCDE中,连接AC,BE,BD,AC与BE,BD分别交于点F,G,若AB=2,则FG的长为( )
A.3﹣
B.﹣1
C.
D.2﹣3
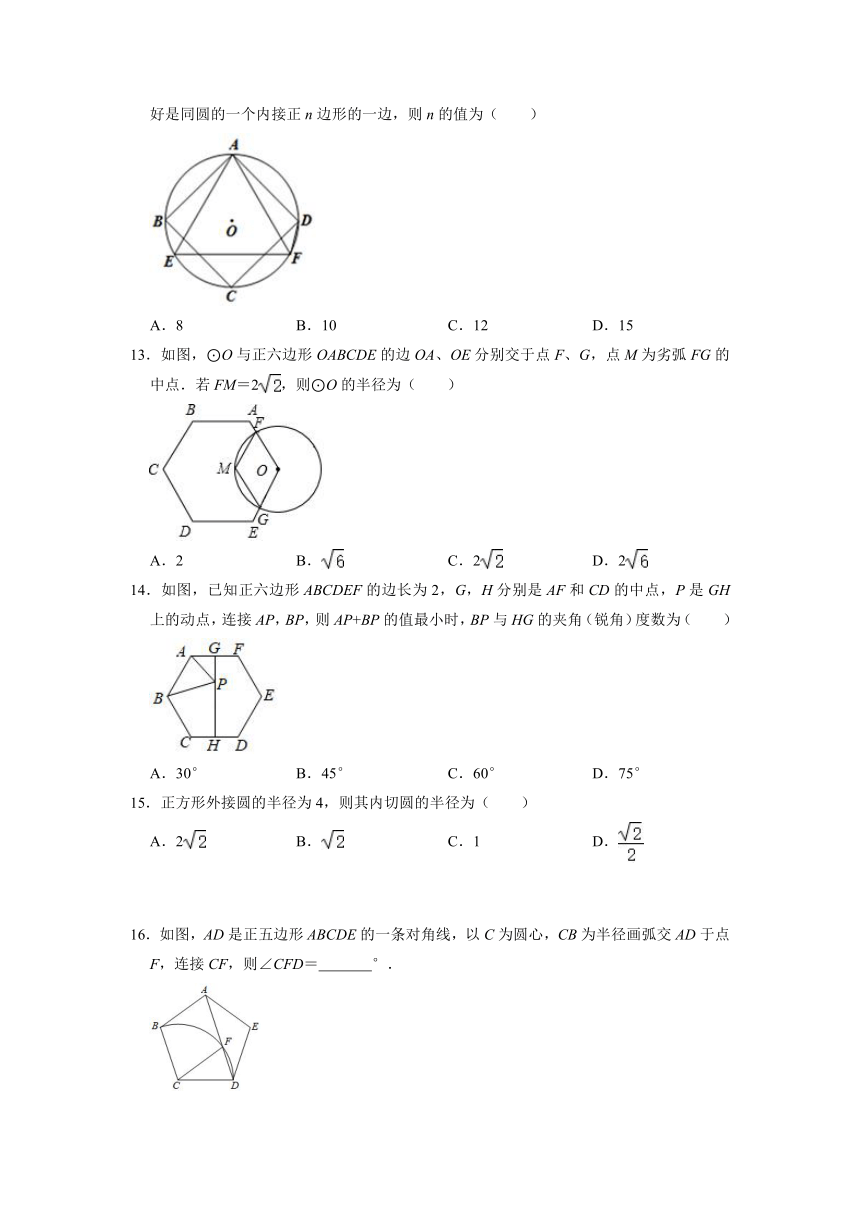
6.已知圆内接正六边形的半径为2,则该内接正六边形的边心距为( )
A.2
B.1
C.
D.
7.已知⊙O的半径是2,一个正方形内接于⊙O,则这个正方形的边长是( )
A.2
B.2
C.
D.4
8.如图,AB,BC和AC分别为⊙O内接正方形,正六边形和正n边形的一边,则n是( )
A.六
B.八
C.十
D.十二
9.如图,正六边形ABCDEF内接于⊙O,过点O作OM⊥边BC于点M,若⊙O的半径为4,则边心距OM的长为( )
A.
B.
C.2
D.
10.如图边长为2+的正方形,剪去四个角成为一个正八边形,则这个正八边形边长为( )
A.0.5
B.
C.1
D.
11.半径为3的正六边形的周长为( )
A.18
B.
C.
D.
12.如图,四边形ABCD为⊙O的内接正四边形,△AEF为⊙O的内接正三角形,若DF恰好是同圆的一个内接正n边形的一边,则n的值为( )
A.8
B.10
C.12
D.15
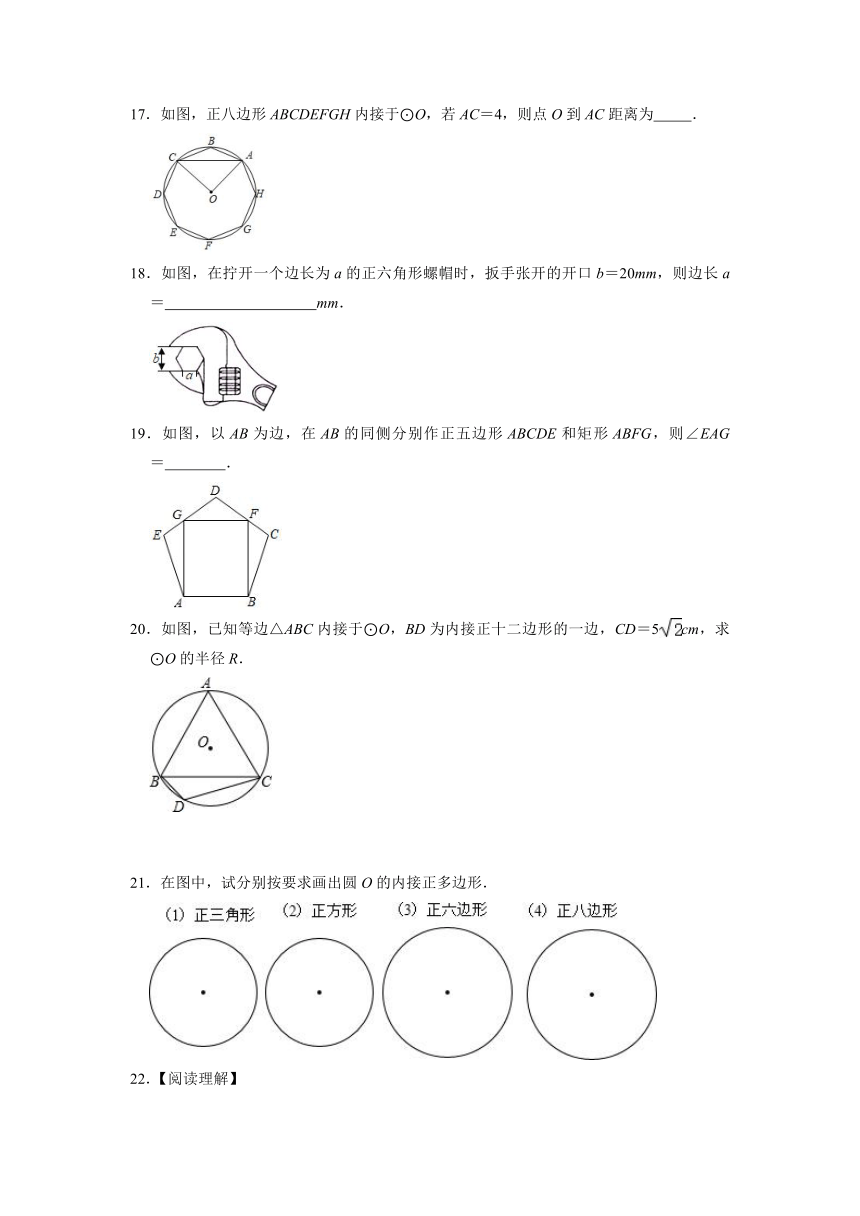
13.如图,⊙O与正六边形OABCDE的边OA、OE分别交于点F、G,点M为劣弧FG的中点.若FM=2,则⊙O的半径为( )
A.2
B.
C.2
D.2
14.如图,已知正六边形ABCDEF的边长为2,G,H分别是AF和CD的中点,P是GH上的动点,连接AP,BP,则AP+BP的值最小时,BP与HG的夹角(锐角)度数为( )
A.30°
B.45°
C.60°
D.75°
15.正方形外接圆的半径为4,则其内切圆的半径为( )
A.2
B.
C.1
D.
16.如图,AD是正五边形ABCDE的一条对角线,以C为圆心,CB为半径画弧交AD于点F,连接CF,则∠CFD=
°.
17.如图,正八边形ABCDEFGH内接于⊙O,若AC=4,则点O到AC距离为
.
18.如图,在拧开一个边长为a的正六角形螺帽时,扳手张开的开口b=20mm,则边长a=
mm.
19.如图,以AB为边,在AB的同侧分别作正五边形ABCDE和矩形ABFG,则∠EAG=
.
20.如图,已知等边△ABC内接于⊙O,BD为内接正十二边形的一边,CD=5cm,求⊙O的半径R.
21.在图中,试分别按要求画出圆O的内接正多边形.
22.【阅读理解】
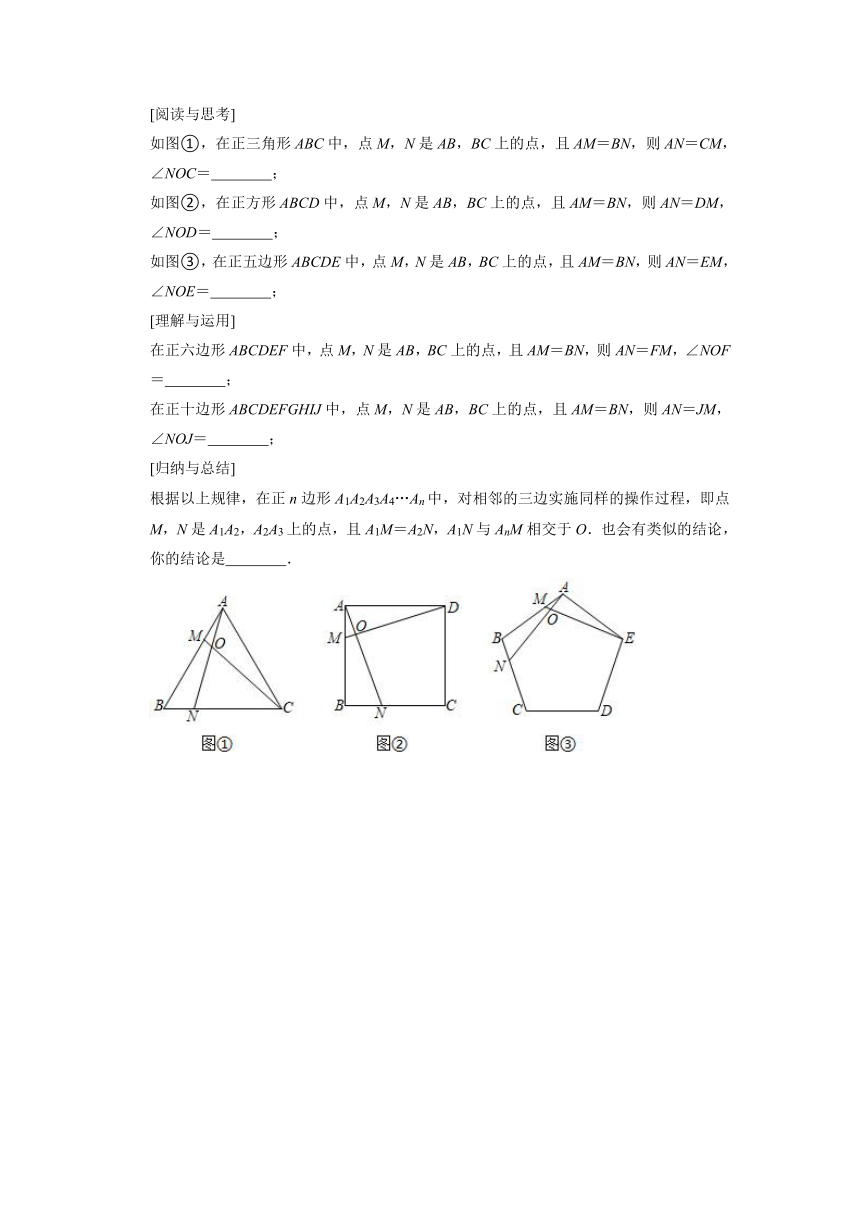
[阅读与思考]
如图①,在正三角形ABC中,点M,N是AB,BC上的点,且AM=BN,则AN=CM,∠NOC=
;
如图②,在正方形ABCD中,点M,N是AB,BC上的点,且AM=BN,则AN=DM,∠NOD=
;
如图③,在正五边形ABCDE中,点M,N是AB,BC上的点,且AM=BN,则AN=EM,∠NOE=
;
[理解与运用]
在正六边形ABCDEF中,点M,N是AB,BC上的点,且AM=BN,则AN=FM,∠NOF=
;
在正十边形ABCDEFGHIJ中,点M,N是AB,BC上的点,且AM=BN,则AN=JM,∠NOJ=
;
[归纳与总结]
根据以上规律,在正n边形A1A2A3A4…An中,对相邻的三边实施同样的操作过程,即点M,N是A1A2,A2A3上的点,且A1M=A2N,A1N与AnM相交于O.也会有类似的结论,你的结论是
.
参考答案
1.解:连接OA,OB,如图所示:
∵六边形ABCDEF是正六边形,
∴∠AOB==60°,
当点P不在上时,
∠APB=∠AOB=30°,
当点P在上时,
∠APB=180°﹣∠AOB=180°﹣30°=150°,
故选:A.
2.解:连接OB,如图所示:
∵A(1,0),O为正六边形的中心,
∴OA=1,∠AOB==60°,
∵OA=OB,
∴△AOB是等边三角形,
∴AB=OA=1,
过B作BG⊥OA于点G,
则AG=OA=,BG=AG=,
∴B(,),
∴C(,),E(,﹣),
∵正六边形的边长=1,
∴正六边形的周长=6,
∵点P的速度为每秒1个单位长度,点Q的速度为每秒2个单位长度,
∴第1次相遇需要的时间为:6÷(1+2)=2(秒),
此时点P的路程为1×2=2,点的Q路程为2×2=4,
此时P,Q相遇地点的坐标在点C(,),
以此类推:第二次相遇地点在点E(,﹣),
第三次相遇地点在点A(﹣1,0),
…如此下去,
∵2021÷3=673…2,
∴第2021次相遇地点在点E,E的坐标为(,﹣),
故选:C.
3.解:连接OA,OB,OE,
∵正方形ABCD内接于⊙O,
∴OA=OB=OE,∠AOB==90°,AB=BC,∠ABC=90°,
∴∠OAB=∠OBA=(180°﹣∠AOB)=45°,
∴∠OBC=∠ABC﹣∠OBA=45°,
∵∠CBE=15°,
∴∠OBE=∠OBC+∠CBE=60°,
∴△OBE是等边三角形,
∴OB=BE=3,
∴OA=3,
∴AB==3,
∴BC=3,
故选:D.
4.解:∵正六边形ABCDEF的边长为1,
∴AD=2,EC=,
∴AD为边的正方形的面积为4,EC为边的正方形的面积为3,
∴两个阴影部分的面积差a﹣b=4﹣3=1,
故选:C.
5.解:∵五边形ABCDE是正五边形,
∴∠BAF=∠ABF=∠DBE=36°,
∴FA=FB,
∴∠ABG=∠AGB=∠BFG=72°,
∴AB=AG=2,BG=BF,
设AF=BF=BG=x,
∵∠BGF=∠AGB,∠GBF=∠GAB,
∴△BGF∽△AGB,
∴BG2=GF?GA,
∴x2=(2﹣x)×2,
∴x2+2x﹣4=0,
∴x=﹣1+或﹣1﹣(舍弃),
∴FG=AG﹣AF=2﹣(﹣1+)=3﹣,
故选:A.
6.解:连接OA,作OM⊥AB,得到∠AOM=30°,AB=2,
则AM=1,
因而OM=,
∴正六边形的边心距是.
故选:C.
7.解:如图所示:
∵四边形ABCD是正方形,
∴∠B=90°,AB=BC,
∴AC是⊙O的直径,△ABC是等腰直角三角形,
∴AC=4,AB=BC=AC=2,
故选:A.
8.解:连接OA,OB,OC.
由题意,∠AOB==90°,∠BOC==60°,
∴∠AOC=∠AOB﹣∠BOC=30°,
∴n==12,
故选:D.
9.解:如图,连接OB、OC.
∵六边形ABCDEF是正六边形,
∴∠BOC=60°,OB=OC=4,
∴△OBC是等边三角形,
∴BC=OB=OC=4,
∵OM⊥BC,
∴BM=CM=2,
在Rt△OBM中,OM===2,
故选:A.
10.解:设正八边形的边长为x,则剪掉的等腰直角三角形的直角边为x,
∵正方形的边长为2+,
∴x+x+x=2+,
解得x==,
∴正八边形的边长为,
故选:D.
11.解:∵正六边形的半径等于边长,
∴正六边形的边长a=3,
正六边形的周长l=6a=18,
故选:A.
12.解:连接OA、OD、OF,如图,
∵AD,AF分别为⊙O的内接正四边形与内接正三角形的一边,
∴∠AOD==90°,∠AOF==120°,
∴∠DOF=∠AOF﹣∠AOD=30°,
∴n==12,
即DF恰好是同圆内接一个正十二边形的一边.
故选:C.
13.解:如图,连接OM,
∵正六边形OABCDE,
∴∠FOG=120°,
∵点M为劣弧FG的中点,
∴∠FOM=60°,OM=OF,
∴△OFM是等边三角形,
∴OM=OF=FM=2.
则⊙O的半径为2.
故选:C.
14.解:如图,连接PF,BF,BF交GH于点P′,连接AP′.
∵正六边形ABCDEF中,G,H分别是AF和CD的中点,
∴GH是正六边形的对称轴,
∴PA=PF,
∴PA+PB=PB+PF,
∵PB+PF≥BF,
∴当点P与点P′重合时,PA+PB的值最小,
∵∠BAF=120°,AB=AF,
∴∠ABF=∠AFB=30°,
∵∠FGP′=90°,
∴∠FP′G=60°,
故选:C.
15.解:如图所示,连接OA、OE,
∵AB是小圆的切线,
∴OE⊥AB,
∵四边形ABCD是正方形,
∴∠OAE=45°,
∴△AOE是等腰直角三角形,AE=OE,
∴OE=OA=×4=2,
故选:A.
16.解:∵五边形ABCDE是正五边形,
∴∠CDE=∠E==108°,AE=DE,
∴∠EDA=∠EAD=(180°﹣∠E)=54°,
∴∠CDF=∠CDE﹣∠EDA=108°﹣36°=72°,
∵CF=CD,
∴∠CFD=∠CDF=72°,
故答案为:72.
17.解:连接OB交AC于M,
∵正八边形ABCDEFGH内接于⊙O,
∴∠AOB=∠BOC==45°,AB=BC,
∴=,∠AOC=90°,
∴AM=CM=AC=2,OM⊥AC,
∵OA=OC,
∠OAM=∠OCA=(180°﹣∠AOC)=45°,
∴∠OAM=∠AOB,
∴AM=OM,
在Rt△AOC中,
∵OA=OC,OA2+OC2=AC2,
∴2OA2=AC2=42=16,
∴OA=2,
在Rt△AOM中,
∵OM2+AM2=OA2,
∴2OM2=(2)2,
∴OM=2,
∴点O到AC距离为2,
故答案为:2.
18.解:如图,连接OC、OD,过O作OH⊥CD于H.
∵∠COD==60°,OC=OD,
∴△COD是等边三角形,
∴∠COH=90°﹣60°=30°,
∵OH⊥CD,
∴CH=DH=CD,OH=b=10(mm),
∴CH=(mm),
∴a=2CH=(mm),
故答案为:.
19.解:∵五边形ABCDE是正五边形,
∴∠EAB=108°,
∵四边形ABFG是矩形,
∴∠BAG=90°,
∴∠EAG=∠EAB﹣∠GAB=108°﹣90°=18°,
故答案为:18°.
20.解:连接OB,OC,OD,
∵等边△ABC内接于⊙O,BD为内接正十二边形的一边,
∴∠BOC=×360°=120°,∠BOD=×360°=30°,
∴∠COD=∠BOC﹣∠BOD=90°,
∵OC=OD,
∴∠OCD=45°,
∴OC=5(cm).
即⊙O的半径R=5cm.
21.解:如图所示:
22.解:[阅读与思考]
∵在正三角形ABC中,点M,N是AB,BC上的点,且AM=BN,
∴∠B=∠CAM,AB=AC,
∵在△ABN和△CAM中
,
∴△ABN≌△CAM(SAS),
∴AN=CM,∠BAN=∠MCA,
∴∠NOC=∠OAC+∠MCA=∠OAC+∠BAN=∠BAC=60°,
故答案为:60°;
∵在正方形ABCD中,点M,N是AB,BC上的点,且AN=DM,
∴AD=AB,
在△ABN和△DAM中,
,
∴△ABN≌△DAM(SAS),
∴∠AMD=∠ANB,∠ADM=∠BAN,
∴∠DON=∠DAN+∠ADM=90°,
答案为:90°;
∵在正五边形ABCDE中,点M,N是AB,BC上的点,且AM=BN,则AN=EM,
∴AB=AE,∠EAM=∠ABN,
∵在△AEM和△BAN中,
,
∴△ABN≌△EAM(SAS),
∴AN=EM,∠AEM=∠BAN,
∴∠EON=∠AEM+∠EAO=108°,
故答案为:108°;
[理解与运用]
∵正三角形的内角度数为:60°,
正方形的内角度数为:90°,
正五边形的内角度数为:108°,
所以同理可得:
在正六边形ABCDEF中,点M,N是AB,BC上的点,且AM=BN,则AN=FM,∠NOF=120°;
故答案为:120°;
同理可得:
在正十边形ABCDEFGHIJ中,点M,N是AB,BC上的点,且AM=BN,则AN=JM,∠NOJ=144°;
故答案为:144°;
[归纳与总结]
根据以上所求的角恰好等于正n边形的内角,
所以所求的角恰好等于正n边形的内角.
故答案为:以上所求的角恰好等于正n边形的内角
1.如图,⊙O是正六边形ABCDEF的外接圆,点P在⊙O上(P不与A,B重合),则∠APB的度数为( )
A.30°或150°
B.60°或120°
C.30°
D.60°
2.如图,点O为正六边形的中心,P、Q分别从点A(﹣1,0)同时出发,沿正六边形按图示方向运动,点P的速度为每秒1个单位长度,点Q的速度为每秒2个单位长度,则第2021次相遇地点的坐标为( )
A.
B.(1,0)
C.
D.(﹣1,0)
3.如图,正方形ABCD内接于⊙O.点E为上一点,连接BE、CE,若∠CBE=15°,BE=3,则BC的长为( )
A.
B.
C.
D.
4.如图,已知正六边形ABCDEF的边长为1,分别以其对角线AD、CE为边作正方形,则两个阴影部分的面积差a﹣b的值为( )
A.0
B.2
C.1
D.
5.如图,在正五边形ABCDE中,连接AC,BE,BD,AC与BE,BD分别交于点F,G,若AB=2,则FG的长为( )
A.3﹣
B.﹣1
C.
D.2﹣3
6.已知圆内接正六边形的半径为2,则该内接正六边形的边心距为( )
A.2
B.1
C.
D.
7.已知⊙O的半径是2,一个正方形内接于⊙O,则这个正方形的边长是( )
A.2
B.2
C.
D.4
8.如图,AB,BC和AC分别为⊙O内接正方形,正六边形和正n边形的一边,则n是( )
A.六
B.八
C.十
D.十二
9.如图,正六边形ABCDEF内接于⊙O,过点O作OM⊥边BC于点M,若⊙O的半径为4,则边心距OM的长为( )
A.
B.
C.2
D.
10.如图边长为2+的正方形,剪去四个角成为一个正八边形,则这个正八边形边长为( )
A.0.5
B.
C.1
D.
11.半径为3的正六边形的周长为( )
A.18
B.
C.
D.
12.如图,四边形ABCD为⊙O的内接正四边形,△AEF为⊙O的内接正三角形,若DF恰好是同圆的一个内接正n边形的一边,则n的值为( )
A.8
B.10
C.12
D.15
13.如图,⊙O与正六边形OABCDE的边OA、OE分别交于点F、G,点M为劣弧FG的中点.若FM=2,则⊙O的半径为( )
A.2
B.
C.2
D.2
14.如图,已知正六边形ABCDEF的边长为2,G,H分别是AF和CD的中点,P是GH上的动点,连接AP,BP,则AP+BP的值最小时,BP与HG的夹角(锐角)度数为( )
A.30°
B.45°
C.60°
D.75°
15.正方形外接圆的半径为4,则其内切圆的半径为( )
A.2
B.
C.1
D.
16.如图,AD是正五边形ABCDE的一条对角线,以C为圆心,CB为半径画弧交AD于点F,连接CF,则∠CFD=
°.
17.如图,正八边形ABCDEFGH内接于⊙O,若AC=4,则点O到AC距离为
.
18.如图,在拧开一个边长为a的正六角形螺帽时,扳手张开的开口b=20mm,则边长a=
mm.
19.如图,以AB为边,在AB的同侧分别作正五边形ABCDE和矩形ABFG,则∠EAG=
.
20.如图,已知等边△ABC内接于⊙O,BD为内接正十二边形的一边,CD=5cm,求⊙O的半径R.
21.在图中,试分别按要求画出圆O的内接正多边形.
22.【阅读理解】
[阅读与思考]
如图①,在正三角形ABC中,点M,N是AB,BC上的点,且AM=BN,则AN=CM,∠NOC=
;
如图②,在正方形ABCD中,点M,N是AB,BC上的点,且AM=BN,则AN=DM,∠NOD=
;
如图③,在正五边形ABCDE中,点M,N是AB,BC上的点,且AM=BN,则AN=EM,∠NOE=
;
[理解与运用]
在正六边形ABCDEF中,点M,N是AB,BC上的点,且AM=BN,则AN=FM,∠NOF=
;
在正十边形ABCDEFGHIJ中,点M,N是AB,BC上的点,且AM=BN,则AN=JM,∠NOJ=
;
[归纳与总结]
根据以上规律,在正n边形A1A2A3A4…An中,对相邻的三边实施同样的操作过程,即点M,N是A1A2,A2A3上的点,且A1M=A2N,A1N与AnM相交于O.也会有类似的结论,你的结论是
.
参考答案
1.解:连接OA,OB,如图所示:
∵六边形ABCDEF是正六边形,
∴∠AOB==60°,
当点P不在上时,
∠APB=∠AOB=30°,
当点P在上时,
∠APB=180°﹣∠AOB=180°﹣30°=150°,
故选:A.
2.解:连接OB,如图所示:
∵A(1,0),O为正六边形的中心,
∴OA=1,∠AOB==60°,
∵OA=OB,
∴△AOB是等边三角形,
∴AB=OA=1,
过B作BG⊥OA于点G,
则AG=OA=,BG=AG=,
∴B(,),
∴C(,),E(,﹣),
∵正六边形的边长=1,
∴正六边形的周长=6,
∵点P的速度为每秒1个单位长度,点Q的速度为每秒2个单位长度,
∴第1次相遇需要的时间为:6÷(1+2)=2(秒),
此时点P的路程为1×2=2,点的Q路程为2×2=4,
此时P,Q相遇地点的坐标在点C(,),
以此类推:第二次相遇地点在点E(,﹣),
第三次相遇地点在点A(﹣1,0),
…如此下去,
∵2021÷3=673…2,
∴第2021次相遇地点在点E,E的坐标为(,﹣),
故选:C.
3.解:连接OA,OB,OE,
∵正方形ABCD内接于⊙O,
∴OA=OB=OE,∠AOB==90°,AB=BC,∠ABC=90°,
∴∠OAB=∠OBA=(180°﹣∠AOB)=45°,
∴∠OBC=∠ABC﹣∠OBA=45°,
∵∠CBE=15°,
∴∠OBE=∠OBC+∠CBE=60°,
∴△OBE是等边三角形,
∴OB=BE=3,
∴OA=3,
∴AB==3,
∴BC=3,
故选:D.
4.解:∵正六边形ABCDEF的边长为1,
∴AD=2,EC=,
∴AD为边的正方形的面积为4,EC为边的正方形的面积为3,
∴两个阴影部分的面积差a﹣b=4﹣3=1,
故选:C.
5.解:∵五边形ABCDE是正五边形,
∴∠BAF=∠ABF=∠DBE=36°,
∴FA=FB,
∴∠ABG=∠AGB=∠BFG=72°,
∴AB=AG=2,BG=BF,
设AF=BF=BG=x,
∵∠BGF=∠AGB,∠GBF=∠GAB,
∴△BGF∽△AGB,
∴BG2=GF?GA,
∴x2=(2﹣x)×2,
∴x2+2x﹣4=0,
∴x=﹣1+或﹣1﹣(舍弃),
∴FG=AG﹣AF=2﹣(﹣1+)=3﹣,
故选:A.
6.解:连接OA,作OM⊥AB,得到∠AOM=30°,AB=2,
则AM=1,
因而OM=,
∴正六边形的边心距是.
故选:C.
7.解:如图所示:
∵四边形ABCD是正方形,
∴∠B=90°,AB=BC,
∴AC是⊙O的直径,△ABC是等腰直角三角形,
∴AC=4,AB=BC=AC=2,
故选:A.
8.解:连接OA,OB,OC.
由题意,∠AOB==90°,∠BOC==60°,
∴∠AOC=∠AOB﹣∠BOC=30°,
∴n==12,
故选:D.
9.解:如图,连接OB、OC.
∵六边形ABCDEF是正六边形,
∴∠BOC=60°,OB=OC=4,
∴△OBC是等边三角形,
∴BC=OB=OC=4,
∵OM⊥BC,
∴BM=CM=2,
在Rt△OBM中,OM===2,
故选:A.
10.解:设正八边形的边长为x,则剪掉的等腰直角三角形的直角边为x,
∵正方形的边长为2+,
∴x+x+x=2+,
解得x==,
∴正八边形的边长为,
故选:D.
11.解:∵正六边形的半径等于边长,
∴正六边形的边长a=3,
正六边形的周长l=6a=18,
故选:A.
12.解:连接OA、OD、OF,如图,
∵AD,AF分别为⊙O的内接正四边形与内接正三角形的一边,
∴∠AOD==90°,∠AOF==120°,
∴∠DOF=∠AOF﹣∠AOD=30°,
∴n==12,
即DF恰好是同圆内接一个正十二边形的一边.
故选:C.
13.解:如图,连接OM,
∵正六边形OABCDE,
∴∠FOG=120°,
∵点M为劣弧FG的中点,
∴∠FOM=60°,OM=OF,
∴△OFM是等边三角形,
∴OM=OF=FM=2.
则⊙O的半径为2.
故选:C.
14.解:如图,连接PF,BF,BF交GH于点P′,连接AP′.
∵正六边形ABCDEF中,G,H分别是AF和CD的中点,
∴GH是正六边形的对称轴,
∴PA=PF,
∴PA+PB=PB+PF,
∵PB+PF≥BF,
∴当点P与点P′重合时,PA+PB的值最小,
∵∠BAF=120°,AB=AF,
∴∠ABF=∠AFB=30°,
∵∠FGP′=90°,
∴∠FP′G=60°,
故选:C.
15.解:如图所示,连接OA、OE,
∵AB是小圆的切线,
∴OE⊥AB,
∵四边形ABCD是正方形,
∴∠OAE=45°,
∴△AOE是等腰直角三角形,AE=OE,
∴OE=OA=×4=2,
故选:A.
16.解:∵五边形ABCDE是正五边形,
∴∠CDE=∠E==108°,AE=DE,
∴∠EDA=∠EAD=(180°﹣∠E)=54°,
∴∠CDF=∠CDE﹣∠EDA=108°﹣36°=72°,
∵CF=CD,
∴∠CFD=∠CDF=72°,
故答案为:72.
17.解:连接OB交AC于M,
∵正八边形ABCDEFGH内接于⊙O,
∴∠AOB=∠BOC==45°,AB=BC,
∴=,∠AOC=90°,
∴AM=CM=AC=2,OM⊥AC,
∵OA=OC,
∠OAM=∠OCA=(180°﹣∠AOC)=45°,
∴∠OAM=∠AOB,
∴AM=OM,
在Rt△AOC中,
∵OA=OC,OA2+OC2=AC2,
∴2OA2=AC2=42=16,
∴OA=2,
在Rt△AOM中,
∵OM2+AM2=OA2,
∴2OM2=(2)2,
∴OM=2,
∴点O到AC距离为2,
故答案为:2.
18.解:如图,连接OC、OD,过O作OH⊥CD于H.
∵∠COD==60°,OC=OD,
∴△COD是等边三角形,
∴∠COH=90°﹣60°=30°,
∵OH⊥CD,
∴CH=DH=CD,OH=b=10(mm),
∴CH=(mm),
∴a=2CH=(mm),
故答案为:.
19.解:∵五边形ABCDE是正五边形,
∴∠EAB=108°,
∵四边形ABFG是矩形,
∴∠BAG=90°,
∴∠EAG=∠EAB﹣∠GAB=108°﹣90°=18°,
故答案为:18°.
20.解:连接OB,OC,OD,
∵等边△ABC内接于⊙O,BD为内接正十二边形的一边,
∴∠BOC=×360°=120°,∠BOD=×360°=30°,
∴∠COD=∠BOC﹣∠BOD=90°,
∵OC=OD,
∴∠OCD=45°,
∴OC=5(cm).
即⊙O的半径R=5cm.
21.解:如图所示:
22.解:[阅读与思考]
∵在正三角形ABC中,点M,N是AB,BC上的点,且AM=BN,
∴∠B=∠CAM,AB=AC,
∵在△ABN和△CAM中
,
∴△ABN≌△CAM(SAS),
∴AN=CM,∠BAN=∠MCA,
∴∠NOC=∠OAC+∠MCA=∠OAC+∠BAN=∠BAC=60°,
故答案为:60°;
∵在正方形ABCD中,点M,N是AB,BC上的点,且AN=DM,
∴AD=AB,
在△ABN和△DAM中,
,
∴△ABN≌△DAM(SAS),
∴∠AMD=∠ANB,∠ADM=∠BAN,
∴∠DON=∠DAN+∠ADM=90°,
答案为:90°;
∵在正五边形ABCDE中,点M,N是AB,BC上的点,且AM=BN,则AN=EM,
∴AB=AE,∠EAM=∠ABN,
∵在△AEM和△BAN中,
,
∴△ABN≌△EAM(SAS),
∴AN=EM,∠AEM=∠BAN,
∴∠EON=∠AEM+∠EAO=108°,
故答案为:108°;
[理解与运用]
∵正三角形的内角度数为:60°,
正方形的内角度数为:90°,
正五边形的内角度数为:108°,
所以同理可得:
在正六边形ABCDEF中,点M,N是AB,BC上的点,且AM=BN,则AN=FM,∠NOF=120°;
故答案为:120°;
同理可得:
在正十边形ABCDEFGHIJ中,点M,N是AB,BC上的点,且AM=BN,则AN=JM,∠NOJ=144°;
故答案为:144°;
[归纳与总结]
根据以上所求的角恰好等于正n边形的内角,
所以所求的角恰好等于正n边形的内角.
故答案为:以上所求的角恰好等于正n边形的内角
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
