2021-2022学年八年级数学苏科版上册 2.4.3角平分线的性质与判定 课前预习练(word版含解析)
文档属性
| 名称 | 2021-2022学年八年级数学苏科版上册 2.4.3角平分线的性质与判定 课前预习练(word版含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 638.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-22 00:00:00 | ||
图片预览


文档简介
2.4.3角平分线的性质与判定
【课前预习练】-2021-2022学年八年级数学上册(苏科版)
一、选择题
1、如图,在中,,平分,,,则点D到AC的距离为(
)
A.4
B.6
C.8
D.10
(1题)
(2题)
(3题)
2、如图所示,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于点D,如果AC=3cm,那么AE+DE等于(
)
A.2cm
B.3cm
C.4cm
D.5cm
3、如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,AB=10,S△ABD=15,则CD的长为( )
A.3
B.4
C.5
D.6
4、如图,△ABC中,∠A=90°,AB=AC,BD平分∠ABE,DE⊥BC,如果BC=10
cm,则△DEC的周长是(
)
A.8
cm
B.10
cm
C.11
cm
D.12
cm
(4题)
(5题)
(6题)
5、如图,在中,平分,且,
则的面积是(
)
A.9
B.12
C.15
D.18
6、如图,点O是△ABC中∠BCA,∠ABC的平分线的交点,已知△ABC的面积是12,周长是8,
则点O到边BC的距离是(
)
A.1
B.2
C.3
D.4
7、三角形中,到三边距离相等的点是(
)
A.三条高线的交点
B.三条中线的交点
C.三条角平分线的交点
D.三边垂直平分线的交点
8、如图,点到、、的距离恰好相等,则点的位置:①在的平分线上;②在的平分线上;③在的平分线上;④恰好是、、三条平分线的交点.上述结论中,正确的个数有(
)
A.个
B.个
C.个
D.个
(8题)
(9题)
9、在正方形网格中,的位置如图所示,到的两边距离相等的点应是(
)
A.点M
B.点Q
C.点P
D.点N
10、如图,直线表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有(
)
A.一处
B.二处
C.三处
D.四处
(10题)
(11题)
(12题)
二、填空题
11、如图,在Rt△ABC中,∠B=90°,以顶点C为圆心,适当长为半径画弧,分别交AC,BC于点E,F,再分别以点E,F为圆心,大于EF的长为半径画弧,两弧交于点P,作射线CP交AB于点D.若BD=3,AC=10,则△ACD的面积是_____.
12、如图,已知△ABC的周长是21,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=4,△ABC的面积是_____.
13、如图所示,已知△ABC的面积是36,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=4,则△ABC的周长是_____.
(13题)
(14题)
(15题)
14、如图,DE⊥AB于点E,DF⊥BC于点F,且DE=DF,若∠DBC=50°,则∠ABC=______(度).
15、如图,已知∠CDA=∠CBA=90°,且CD=CB,则点C在∠________的平分线上,
点A在∠__________的平分线上.
16、如图,在△ABC中,∠ABC=110°,∠ACB=40°,CE是∠ACB的角平分线,D是AC上一点,若∠CBD=40°,则∠CED=__________.
三、解答题
17、如图,在平行四边形ABCD中,AB=4,BC=6.
(1)用无刻度的直尺和圆规作∠ABC的平分线,交AD于点E;(不要求写作法,但要保留清晰的作图痕述)
(2)求(1)中DE的长.
18、已知,如图,PB、PC分别是△ABC的外角平分线,且相交于点P
求证:点P在∠A的平分线上。
19、如图,点E,F分别在OA,OB上,DE=DF,∠OED+∠OFD=180°,求证:OD平分∠AOB
20、如图,BE=CF,DE⊥AB,垂足为E,DF⊥AC,垂足为F,且DB=DC.
求证:(1)Rt△BED≌Rt△CFD;
(2)AD是∠BAC的平分线.
21、如图,已知△ABC中BC边上的垂直平分线DE与∠BAC得平分线交于点E,EF⊥AB交AB的延长线于点F,EG⊥AC交于点G.
求证:(1)BF=CG;(2)AF=(AB+AC).
2.4.3角平分线的性质与判定
【课前预习练】-2021-2022学年八年级数学上册(苏科版)(含答案)
一、选择题
1、如图,在中,,平分,,,则点D到AC的距离为(
)
A.4
B.6
C.8
D.10
【答案】A
【分析】由D在∠BAC的平分线AD上得,点D到AC的距离与点D到AB的距离BD相等,因此求得BD的长即可.
【详解】解:∵BC=10,CD=6,∴BD=4.
∵∠B=90°,AD平分∠BAC
.
由角平分线的性质,得点D到AC的距离等于BD=4.
故选:A.
2、如图所示,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于点D,如果AC=3cm,那么AE+DE等于(
)
A.2cm
B.3cm
C.4cm
D.5cm
【答案】B
【分析】直接利用角平分线的性质得出DE=EC,进而得出答案.
【详解】解:∵△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于点D,
∴EC=DE,
∴AE+DE=AE+EC=3cm.
故选:B.
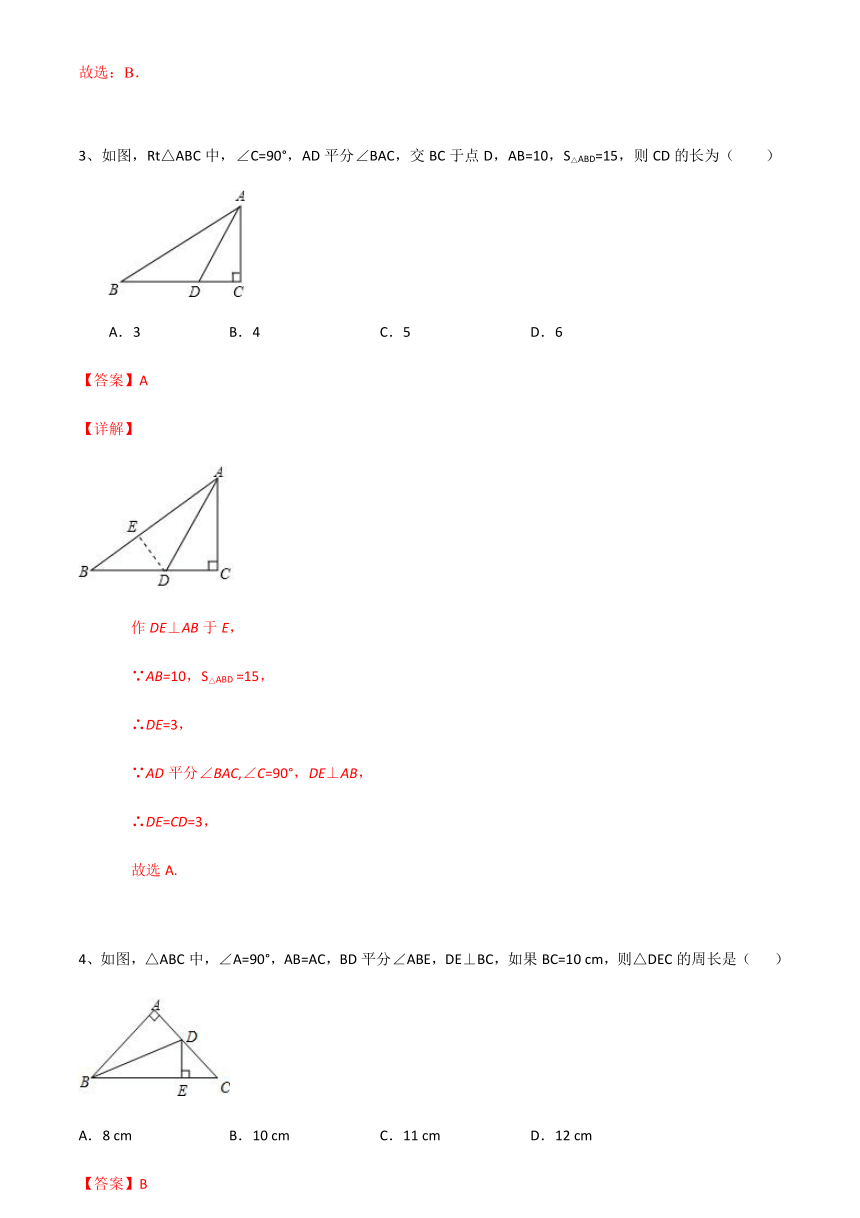
3、如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,AB=10,S△ABD=15,则CD的长为( )
A.3
B.4
C.5
D.6
【答案】A
【详解】
作DE⊥AB于E,
∵AB=10,S△ABD
=15,
∴DE=3,
∵AD平分∠BAC,∠C=90°,DE⊥AB,
∴DE=CD=3,
故选A.
4、如图,△ABC中,∠A=90°,AB=AC,BD平分∠ABE,DE⊥BC,如果BC=10
cm,则△DEC的周长是(
)
A.8
cm
B.10
cm
C.11
cm
D.12
cm
【答案】B
【提示】
根据角平分线的性质,得AD=DE,利用HL判定△BAD≌△BED,
得出AB=BE,进而得出BC=DE+DC+EC=10cm.
【详解】
解:BD平分∠ABE,DE⊥BC,DA⊥AB
AD=DE
又BD=BD,△BAD≌△BED
(HL)
AB=BE
又AB=AC
BE=AC
BC=BE+EC=AC+EC=AD+DC+EC=DE+DC+EC=10cm
△DEC的周长是10cm,
故选B.
5、如图,在中,平分,且,
则的面积是(
)
A.9
B.12
C.15
D.18
【答案】C
【分析】作DE⊥AB,根据角平分线的性质得到DE=
CD=2,再根据三角形的面积公式即可求解.
【详解】如图,作DE⊥AB,
∵平分,
∴DE=CD=2
∴S△ABC=S△ABD+S△DBC=AB×DE+BC×CD=×9×2+×6×2=15
故选C.
6、如图,点O是△ABC中∠BCA,∠ABC的平分线的交点,已知△ABC的面积是12,周长是8,
则点O到边BC的距离是(
)
A.1
B.2
C.3
D.4
【答案】C
【提示】过点O作OE⊥AB于E,OF⊥AC于F,连接OA,根据角平分线的性质得:OE=OF=OD然后根据△ABC的面积是12,周长是8,即可得出点O到边BC的距离.
【详解】如图,过点O作OE⊥AB于E,OF⊥AC于F,连接OA.
∵点O是∠ABC,∠ACB平分线的交点,
∴OE=OD,OF=OD,即OE=OF=OD
∴S△ABC=S△ABO+S△BCO+S△ACO=AB·OE+BC·OD+AC·OF
=×OD×(AB+BC+AC)=×OD×8=12
OD=3
故选:C
7、三角形中,到三边距离相等的点是(
)
A.三条高线的交点
B.三条中线的交点
C.三条角平分线的交点
D.三边垂直平分线的交点
【答案】C
【分析】根据角平分线的性质:角平分线上的点到角两边的距离相等,即可得出结论.
【详解】解:三角形中,到三边距离相等的点是三条角平分线的交点
故选C.
8、如图,点到、、的距离恰好相等,则点的位置:①在的平分线上;②在的平分线上;③在的平分线上;④恰好是、、三条平分线的交点.上述结论中,正确的个数有(
)
A.个
B.个
C.个
D.个
【答案】D
【分析】利用角平分线的判定定理分析.由已知点P到BE,BD,AC的距离恰好相等进行思考,首先到到两边距离相等,得出结论,然后另外两边再得结论,如此这样,答案可得.
【详解】∵点P到BE,BD的距离相等,∴点P在∠B的平分线上,故①正确;
∵点P到BD、AC的距离相等,∴点P在∠DAC的平分线上,故②正确;
∵点P到BE、AC的距离相等,∴点P在∠ECA的平分线上,故③正确;
∵点P到BE、BD、AC的距离都相等,∴恰好是∠B、∠DAC、∠ECA三条平分线的交点,故④正确;
综上可得①②③④都正确.
故选:D.
9、在正方形网格中,的位置如图所示,到的两边距离相等的点应是(
)
A.点M
B.点Q
C.点P
D.点N
【答案】A
【详解】
解:观察图形可知点M在的角平分线上,
∴点M到的两边距离相等
故选:A
10、如图,直线表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有(
)
A.一处
B.二处
C.三处
D.四处
【答案】D
【分析】
由三角形内角平分线的交点到三角形三边的距离相等,可得三角形内角平分线的交点满足条件;然后利用角平分线的性质,可证得三角形两条外角平分线的交点到其三边的距离也相等,这样的点有3个,可得可供选择的地址有4个.
【详解】
解:∵△ABC内角平分线的交点到三角形三边的距离相等,
∴△ABC内角平分线的交点满足条件;
如图:点P是△ABC两条外角平分线的交点,
过点P作PE⊥AB,PD⊥BC,PF⊥AC,
∴PE=PF,PF=PD,
∴PE=PF=PD,
∴点P到△ABC的三边的距离相等,
∴△ABC两条外角平分线的交点到其三边的距离也相等,满足这条件的点有3个;
综上,到三条公路的距离相等的点有4处,
∴可供选择的地址有4处.
故选:D
二、填空题
11、如图,在Rt△ABC中,∠B=90°,以顶点C为圆心,适当长为半径画弧,分别交AC,BC于点E,F,再分别以点E,F为圆心,大于EF的长为半径画弧,两弧交于点P,作射线CP交AB于点D.若BD=3,AC=10,则△ACD的面积是_____.
【答案】15
【详解】
解:如图,过点D作DQ⊥AC于点Q,
由作图知CP是∠ACB的平分线,
∵∠B=90°,BD=3,∴DB=DQ=3,
∵AC=10,∴S△ACD=?AC?DQ=×10×3=15,
故答案为15.
12、如图,已知△ABC的周长是21,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=4,△ABC的面积是_____.
【答案】42
【详解】
解:连接AO,可知AO平分∠BAC,由角平分线的性质可知
点O到AB、AC、BC的距离相等,
把求△ABC的面积转化为求△AOB、△AOC、△BOC的面积之和,
即
13、如图所示,已知△ABC的面积是36,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=4,则△ABC的周长是_____.
【答案】18
【详解】
如图,
过点O作OE⊥AB于E,作OF⊥AC于F,
∵OB、OC分别平分∠ABC和∠ACB,OD⊥BC,
∴OE=OF=OD=4,
∵S△ABC==2·△ABC的周长,
∴△ABC的周长=36÷2=18,
故答案为18.
14、如图,DE⊥AB于点E,DF⊥BC于点F,且DE=DF,若∠DBC=50°,则∠ABC=______(度).
试题分析:根据到角的两边的距离相等的点在角平分线上可得BD平分∠ABC,再根据∠DBC=50°可得答案.
试题解析:∵DE⊥AB于点E,DF⊥BC于点F,且DE=DF,
∴BD平分∠ABC,
∴∠ABC=2∠DBC,
∵∠DBC=50°,
∴∠ABC=100°,
故答案为:100.
15、如图,已知∠CDA=∠CBA=90°,且CD=CB,则点C在∠________的平分线上,
点A在∠__________的平分线上.
试题分析:从已知条件进行思考,根据角平分线的逆定理可得答案.
试题解析:∵∠CDA=∠CBA=90°,且CD=CB,
根据角平分线性质的逆定理,则点C在∠BAD的平分线上,点A在∠BCD的平分线上.
故填∠BAD,∠BCD.
16、如图,在△ABC中,∠ABC=110°,∠ACB=40°,CE是∠ACB的角平分线,D是AC上一点,若∠CBD=40°,则∠CED=__________.
试题分析:作EN⊥BD,EM⊥BC,EH⊥AC,垂足分别是N
M
H,根据三角形的内角和定理求出∠ABD,∠ABM=70°,根据角平分线性质求出EN=EM=EH,推出DE是∠ADB的平分线,求出∠ADE=∠ACB=40°,根据平行线的性质和判定即可求出结论.
试题解析:∠A=180°-∠ACB-∠ABC=180°-110°-40°=30°,
∵作EN⊥BD,EM⊥BC,EH⊥AC,垂足分别是N、M、H,∠ABC=110°,∠CBD=40°,
∴∠ABD=70°,
∴∠ABC的外角是∠ABM=180°-110°=70°;
∴BE是∠DBM的角平分线,∴EM=EN,
∵CE是∠ACB的平分线,EM⊥CB,EH⊥AC,∴EM=EH,∴EH=EN,
∴DE是∠ADB的平分线,
∵∠ADB=180°-∠A-∠ABD=180°-30°-70°=80°,
∴∠ADE=∠ADB=40°=∠ACB,∴DE∥CB,∴∠CED=∠ECB=20°
故答案为:20°.
三、解答题
17、如图,在平行四边形ABCD中,AB=4,BC=6.
(1)用无刻度的直尺和圆规作∠ABC的平分线,交AD于点E;(不要求写作法,但要保留清晰的作图痕述)
(2)求(1)中DE的长.
【答案】(1)图见解析;(2)2.
【详解】
(1)分以下三步:
①以点B为圆心,小于AB长为半径画弧,分别交AB于点M,交BC于点N
②分别以点M、N为圆心,大于长为半径画弧,两弧交于点O
③过点B、O作射线,交AD于点E
则BE即为所作,如图所示:
(2)∵四边形ABCD是平行四边形,
∴
∵BE平分
∴
∵
∴
∴
∴
∴.
18、已知,如图,PB、PC分别是△ABC的外角平分线,且相交于点P
求证:点P在∠A的平分线上。
试题分析:作PM⊥AB于M,PN⊥BC于N,PE⊥AC于E,根据角平分线性质得出PM=PN,PN=PE,推出PM=PE,根据角平分线性质推出即可。
证明:作PM⊥AB于M,PN⊥BC于N,PE⊥AC于E,
∵PB、PC分别是△ABC的外角平分线,
∴PM=PN,PN=PE,
∴PM=PE,
∵PM⊥AB,PE⊥AC,
∴点P在∠A的平分线上。
19、如图,点E,F分别在OA,OB上,DE=DF,∠OED+∠OFD=180°,求证:OD平分∠AOB
试题分析:
过点D作DM⊥OA于M,DN⊥OB于N,进而得出△EDM≌△FDN,由全等三角形的性质得出DM=DN,从而得出结论。
证明:过点D作DM⊥OA于M,DN⊥OB于N,
∴∠DME=∠DNF=90°.
∵∠OED+∠OFD=180°,且∠OED+∠MED=180°,
∴∠MED=∠OFD.
在△EDM和△FDN中,
?∠DME=∠DNF,
∠MED=∠OFD,
DE=DF,
∴△EDM≌△FDN(AAS),
∴DM=DN.
∵DM⊥OA,DN⊥OB,
∴OD平分∠AOB.
20、如图,BE=CF,DE⊥AB,垂足为E,DF⊥AC,垂足为F,且DB=DC.
求证:(1)Rt△BED≌Rt△CFD;
(2)AD是∠BAC的平分线.
试题分析:(1)根据直角三角形全等的判定HL证出即可;
(2)由(1)推出DE=DF,根据角平分线性质推出即可.
试题解析:证明:(1)∵DE⊥AB,DF⊥AC,
∴∠E=∠DFC=90°,
在Rt△BED和Rt△CFD中
,
∴Rt△BED≌Rt△CFD(HL).
证明:(2)∵Rt△BED≌Rt△CFD,
∴DE=DF,
∵DE⊥AB,DF⊥AC,
∴AD是∠BAC的平分线.
21、如图,已知△ABC中BC边上的垂直平分线DE与∠BAC得平分线交于点E,EF⊥AB交AB的延长线于点F,EG⊥AC交于点G.
求证:(1)BF=CG;(2)AF=(AB+AC).
【解析】
证明:(1)连接BE和CE,
∵DE是BC的垂直平分线,∴BE=CE,
∵AE平分∠BAC,EF⊥AB,EG⊥AC,
∴∠BFE=∠EGC=90°,EF=EG,
在Rt△BFE和Rt△CGE中
∴Rt△BFE≌Rt△CGE(HL),∴BF=CG;
(2)∵AE平分∠BAC,EF⊥AB,EG⊥AC,
∴∠AFE=∠AGE=90°,∠FAE=∠GAE,
在△AFE和△AGE中
∴△AFE≌△AGE,∴AF=AG,
∵BF=CG,∴(AB+AC)=(AF-BF+AG+CG)=(AF+AF)=AF,
即AF=(AB+AC).
【课前预习练】-2021-2022学年八年级数学上册(苏科版)
一、选择题
1、如图,在中,,平分,,,则点D到AC的距离为(
)
A.4
B.6
C.8
D.10
(1题)
(2题)
(3题)
2、如图所示,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于点D,如果AC=3cm,那么AE+DE等于(
)
A.2cm
B.3cm
C.4cm
D.5cm
3、如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,AB=10,S△ABD=15,则CD的长为( )
A.3
B.4
C.5
D.6
4、如图,△ABC中,∠A=90°,AB=AC,BD平分∠ABE,DE⊥BC,如果BC=10
cm,则△DEC的周长是(
)
A.8
cm
B.10
cm
C.11
cm
D.12
cm
(4题)
(5题)
(6题)
5、如图,在中,平分,且,
则的面积是(
)
A.9
B.12
C.15
D.18
6、如图,点O是△ABC中∠BCA,∠ABC的平分线的交点,已知△ABC的面积是12,周长是8,
则点O到边BC的距离是(
)
A.1
B.2
C.3
D.4
7、三角形中,到三边距离相等的点是(
)
A.三条高线的交点
B.三条中线的交点
C.三条角平分线的交点
D.三边垂直平分线的交点
8、如图,点到、、的距离恰好相等,则点的位置:①在的平分线上;②在的平分线上;③在的平分线上;④恰好是、、三条平分线的交点.上述结论中,正确的个数有(
)
A.个
B.个
C.个
D.个
(8题)
(9题)
9、在正方形网格中,的位置如图所示,到的两边距离相等的点应是(
)
A.点M
B.点Q
C.点P
D.点N
10、如图,直线表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有(
)
A.一处
B.二处
C.三处
D.四处
(10题)
(11题)
(12题)
二、填空题
11、如图,在Rt△ABC中,∠B=90°,以顶点C为圆心,适当长为半径画弧,分别交AC,BC于点E,F,再分别以点E,F为圆心,大于EF的长为半径画弧,两弧交于点P,作射线CP交AB于点D.若BD=3,AC=10,则△ACD的面积是_____.
12、如图,已知△ABC的周长是21,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=4,△ABC的面积是_____.
13、如图所示,已知△ABC的面积是36,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=4,则△ABC的周长是_____.
(13题)
(14题)
(15题)
14、如图,DE⊥AB于点E,DF⊥BC于点F,且DE=DF,若∠DBC=50°,则∠ABC=______(度).
15、如图,已知∠CDA=∠CBA=90°,且CD=CB,则点C在∠________的平分线上,
点A在∠__________的平分线上.
16、如图,在△ABC中,∠ABC=110°,∠ACB=40°,CE是∠ACB的角平分线,D是AC上一点,若∠CBD=40°,则∠CED=__________.
三、解答题
17、如图,在平行四边形ABCD中,AB=4,BC=6.
(1)用无刻度的直尺和圆规作∠ABC的平分线,交AD于点E;(不要求写作法,但要保留清晰的作图痕述)
(2)求(1)中DE的长.
18、已知,如图,PB、PC分别是△ABC的外角平分线,且相交于点P
求证:点P在∠A的平分线上。
19、如图,点E,F分别在OA,OB上,DE=DF,∠OED+∠OFD=180°,求证:OD平分∠AOB
20、如图,BE=CF,DE⊥AB,垂足为E,DF⊥AC,垂足为F,且DB=DC.
求证:(1)Rt△BED≌Rt△CFD;
(2)AD是∠BAC的平分线.
21、如图,已知△ABC中BC边上的垂直平分线DE与∠BAC得平分线交于点E,EF⊥AB交AB的延长线于点F,EG⊥AC交于点G.
求证:(1)BF=CG;(2)AF=(AB+AC).
2.4.3角平分线的性质与判定
【课前预习练】-2021-2022学年八年级数学上册(苏科版)(含答案)
一、选择题
1、如图,在中,,平分,,,则点D到AC的距离为(
)
A.4
B.6
C.8
D.10
【答案】A
【分析】由D在∠BAC的平分线AD上得,点D到AC的距离与点D到AB的距离BD相等,因此求得BD的长即可.
【详解】解:∵BC=10,CD=6,∴BD=4.
∵∠B=90°,AD平分∠BAC
.
由角平分线的性质,得点D到AC的距离等于BD=4.
故选:A.
2、如图所示,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于点D,如果AC=3cm,那么AE+DE等于(
)
A.2cm
B.3cm
C.4cm
D.5cm
【答案】B
【分析】直接利用角平分线的性质得出DE=EC,进而得出答案.
【详解】解:∵△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于点D,
∴EC=DE,
∴AE+DE=AE+EC=3cm.
故选:B.
3、如图,Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,AB=10,S△ABD=15,则CD的长为( )
A.3
B.4
C.5
D.6
【答案】A
【详解】
作DE⊥AB于E,
∵AB=10,S△ABD
=15,
∴DE=3,
∵AD平分∠BAC,∠C=90°,DE⊥AB,
∴DE=CD=3,
故选A.
4、如图,△ABC中,∠A=90°,AB=AC,BD平分∠ABE,DE⊥BC,如果BC=10
cm,则△DEC的周长是(
)
A.8
cm
B.10
cm
C.11
cm
D.12
cm
【答案】B
【提示】
根据角平分线的性质,得AD=DE,利用HL判定△BAD≌△BED,
得出AB=BE,进而得出BC=DE+DC+EC=10cm.
【详解】
解:BD平分∠ABE,DE⊥BC,DA⊥AB
AD=DE
又BD=BD,△BAD≌△BED
(HL)
AB=BE
又AB=AC
BE=AC
BC=BE+EC=AC+EC=AD+DC+EC=DE+DC+EC=10cm
△DEC的周长是10cm,
故选B.
5、如图,在中,平分,且,
则的面积是(
)
A.9
B.12
C.15
D.18
【答案】C
【分析】作DE⊥AB,根据角平分线的性质得到DE=
CD=2,再根据三角形的面积公式即可求解.
【详解】如图,作DE⊥AB,
∵平分,
∴DE=CD=2
∴S△ABC=S△ABD+S△DBC=AB×DE+BC×CD=×9×2+×6×2=15
故选C.
6、如图,点O是△ABC中∠BCA,∠ABC的平分线的交点,已知△ABC的面积是12,周长是8,
则点O到边BC的距离是(
)
A.1
B.2
C.3
D.4
【答案】C
【提示】过点O作OE⊥AB于E,OF⊥AC于F,连接OA,根据角平分线的性质得:OE=OF=OD然后根据△ABC的面积是12,周长是8,即可得出点O到边BC的距离.
【详解】如图,过点O作OE⊥AB于E,OF⊥AC于F,连接OA.
∵点O是∠ABC,∠ACB平分线的交点,
∴OE=OD,OF=OD,即OE=OF=OD
∴S△ABC=S△ABO+S△BCO+S△ACO=AB·OE+BC·OD+AC·OF
=×OD×(AB+BC+AC)=×OD×8=12
OD=3
故选:C
7、三角形中,到三边距离相等的点是(
)
A.三条高线的交点
B.三条中线的交点
C.三条角平分线的交点
D.三边垂直平分线的交点
【答案】C
【分析】根据角平分线的性质:角平分线上的点到角两边的距离相等,即可得出结论.
【详解】解:三角形中,到三边距离相等的点是三条角平分线的交点
故选C.
8、如图,点到、、的距离恰好相等,则点的位置:①在的平分线上;②在的平分线上;③在的平分线上;④恰好是、、三条平分线的交点.上述结论中,正确的个数有(
)
A.个
B.个
C.个
D.个
【答案】D
【分析】利用角平分线的判定定理分析.由已知点P到BE,BD,AC的距离恰好相等进行思考,首先到到两边距离相等,得出结论,然后另外两边再得结论,如此这样,答案可得.
【详解】∵点P到BE,BD的距离相等,∴点P在∠B的平分线上,故①正确;
∵点P到BD、AC的距离相等,∴点P在∠DAC的平分线上,故②正确;
∵点P到BE、AC的距离相等,∴点P在∠ECA的平分线上,故③正确;
∵点P到BE、BD、AC的距离都相等,∴恰好是∠B、∠DAC、∠ECA三条平分线的交点,故④正确;
综上可得①②③④都正确.
故选:D.
9、在正方形网格中,的位置如图所示,到的两边距离相等的点应是(
)
A.点M
B.点Q
C.点P
D.点N
【答案】A
【详解】
解:观察图形可知点M在的角平分线上,
∴点M到的两边距离相等
故选:A
10、如图,直线表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有(
)
A.一处
B.二处
C.三处
D.四处
【答案】D
【分析】
由三角形内角平分线的交点到三角形三边的距离相等,可得三角形内角平分线的交点满足条件;然后利用角平分线的性质,可证得三角形两条外角平分线的交点到其三边的距离也相等,这样的点有3个,可得可供选择的地址有4个.
【详解】
解:∵△ABC内角平分线的交点到三角形三边的距离相等,
∴△ABC内角平分线的交点满足条件;
如图:点P是△ABC两条外角平分线的交点,
过点P作PE⊥AB,PD⊥BC,PF⊥AC,
∴PE=PF,PF=PD,
∴PE=PF=PD,
∴点P到△ABC的三边的距离相等,
∴△ABC两条外角平分线的交点到其三边的距离也相等,满足这条件的点有3个;
综上,到三条公路的距离相等的点有4处,
∴可供选择的地址有4处.
故选:D
二、填空题
11、如图,在Rt△ABC中,∠B=90°,以顶点C为圆心,适当长为半径画弧,分别交AC,BC于点E,F,再分别以点E,F为圆心,大于EF的长为半径画弧,两弧交于点P,作射线CP交AB于点D.若BD=3,AC=10,则△ACD的面积是_____.
【答案】15
【详解】
解:如图,过点D作DQ⊥AC于点Q,
由作图知CP是∠ACB的平分线,
∵∠B=90°,BD=3,∴DB=DQ=3,
∵AC=10,∴S△ACD=?AC?DQ=×10×3=15,
故答案为15.
12、如图,已知△ABC的周长是21,OB,OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=4,△ABC的面积是_____.
【答案】42
【详解】
解:连接AO,可知AO平分∠BAC,由角平分线的性质可知
点O到AB、AC、BC的距离相等,
把求△ABC的面积转化为求△AOB、△AOC、△BOC的面积之和,
即
13、如图所示,已知△ABC的面积是36,OB、OC分别平分∠ABC和∠ACB,OD⊥BC于D,且OD=4,则△ABC的周长是_____.
【答案】18
【详解】
如图,
过点O作OE⊥AB于E,作OF⊥AC于F,
∵OB、OC分别平分∠ABC和∠ACB,OD⊥BC,
∴OE=OF=OD=4,
∵S△ABC==2·△ABC的周长,
∴△ABC的周长=36÷2=18,
故答案为18.
14、如图,DE⊥AB于点E,DF⊥BC于点F,且DE=DF,若∠DBC=50°,则∠ABC=______(度).
试题分析:根据到角的两边的距离相等的点在角平分线上可得BD平分∠ABC,再根据∠DBC=50°可得答案.
试题解析:∵DE⊥AB于点E,DF⊥BC于点F,且DE=DF,
∴BD平分∠ABC,
∴∠ABC=2∠DBC,
∵∠DBC=50°,
∴∠ABC=100°,
故答案为:100.
15、如图,已知∠CDA=∠CBA=90°,且CD=CB,则点C在∠________的平分线上,
点A在∠__________的平分线上.
试题分析:从已知条件进行思考,根据角平分线的逆定理可得答案.
试题解析:∵∠CDA=∠CBA=90°,且CD=CB,
根据角平分线性质的逆定理,则点C在∠BAD的平分线上,点A在∠BCD的平分线上.
故填∠BAD,∠BCD.
16、如图,在△ABC中,∠ABC=110°,∠ACB=40°,CE是∠ACB的角平分线,D是AC上一点,若∠CBD=40°,则∠CED=__________.
试题分析:作EN⊥BD,EM⊥BC,EH⊥AC,垂足分别是N
M
H,根据三角形的内角和定理求出∠ABD,∠ABM=70°,根据角平分线性质求出EN=EM=EH,推出DE是∠ADB的平分线,求出∠ADE=∠ACB=40°,根据平行线的性质和判定即可求出结论.
试题解析:∠A=180°-∠ACB-∠ABC=180°-110°-40°=30°,
∵作EN⊥BD,EM⊥BC,EH⊥AC,垂足分别是N、M、H,∠ABC=110°,∠CBD=40°,
∴∠ABD=70°,
∴∠ABC的外角是∠ABM=180°-110°=70°;
∴BE是∠DBM的角平分线,∴EM=EN,
∵CE是∠ACB的平分线,EM⊥CB,EH⊥AC,∴EM=EH,∴EH=EN,
∴DE是∠ADB的平分线,
∵∠ADB=180°-∠A-∠ABD=180°-30°-70°=80°,
∴∠ADE=∠ADB=40°=∠ACB,∴DE∥CB,∴∠CED=∠ECB=20°
故答案为:20°.
三、解答题
17、如图,在平行四边形ABCD中,AB=4,BC=6.
(1)用无刻度的直尺和圆规作∠ABC的平分线,交AD于点E;(不要求写作法,但要保留清晰的作图痕述)
(2)求(1)中DE的长.
【答案】(1)图见解析;(2)2.
【详解】
(1)分以下三步:
①以点B为圆心,小于AB长为半径画弧,分别交AB于点M,交BC于点N
②分别以点M、N为圆心,大于长为半径画弧,两弧交于点O
③过点B、O作射线,交AD于点E
则BE即为所作,如图所示:
(2)∵四边形ABCD是平行四边形,
∴
∵BE平分
∴
∵
∴
∴
∴
∴.
18、已知,如图,PB、PC分别是△ABC的外角平分线,且相交于点P
求证:点P在∠A的平分线上。
试题分析:作PM⊥AB于M,PN⊥BC于N,PE⊥AC于E,根据角平分线性质得出PM=PN,PN=PE,推出PM=PE,根据角平分线性质推出即可。
证明:作PM⊥AB于M,PN⊥BC于N,PE⊥AC于E,
∵PB、PC分别是△ABC的外角平分线,
∴PM=PN,PN=PE,
∴PM=PE,
∵PM⊥AB,PE⊥AC,
∴点P在∠A的平分线上。
19、如图,点E,F分别在OA,OB上,DE=DF,∠OED+∠OFD=180°,求证:OD平分∠AOB
试题分析:
过点D作DM⊥OA于M,DN⊥OB于N,进而得出△EDM≌△FDN,由全等三角形的性质得出DM=DN,从而得出结论。
证明:过点D作DM⊥OA于M,DN⊥OB于N,
∴∠DME=∠DNF=90°.
∵∠OED+∠OFD=180°,且∠OED+∠MED=180°,
∴∠MED=∠OFD.
在△EDM和△FDN中,
?∠DME=∠DNF,
∠MED=∠OFD,
DE=DF,
∴△EDM≌△FDN(AAS),
∴DM=DN.
∵DM⊥OA,DN⊥OB,
∴OD平分∠AOB.
20、如图,BE=CF,DE⊥AB,垂足为E,DF⊥AC,垂足为F,且DB=DC.
求证:(1)Rt△BED≌Rt△CFD;
(2)AD是∠BAC的平分线.
试题分析:(1)根据直角三角形全等的判定HL证出即可;
(2)由(1)推出DE=DF,根据角平分线性质推出即可.
试题解析:证明:(1)∵DE⊥AB,DF⊥AC,
∴∠E=∠DFC=90°,
在Rt△BED和Rt△CFD中
,
∴Rt△BED≌Rt△CFD(HL).
证明:(2)∵Rt△BED≌Rt△CFD,
∴DE=DF,
∵DE⊥AB,DF⊥AC,
∴AD是∠BAC的平分线.
21、如图,已知△ABC中BC边上的垂直平分线DE与∠BAC得平分线交于点E,EF⊥AB交AB的延长线于点F,EG⊥AC交于点G.
求证:(1)BF=CG;(2)AF=(AB+AC).
【解析】
证明:(1)连接BE和CE,
∵DE是BC的垂直平分线,∴BE=CE,
∵AE平分∠BAC,EF⊥AB,EG⊥AC,
∴∠BFE=∠EGC=90°,EF=EG,
在Rt△BFE和Rt△CGE中
∴Rt△BFE≌Rt△CGE(HL),∴BF=CG;
(2)∵AE平分∠BAC,EF⊥AB,EG⊥AC,
∴∠AFE=∠AGE=90°,∠FAE=∠GAE,
在△AFE和△AGE中
∴△AFE≌△AGE,∴AF=AG,
∵BF=CG,∴(AB+AC)=(AF-BF+AG+CG)=(AF+AF)=AF,
即AF=(AB+AC).
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
