2021-2022学年苏科版八年级数学上册1.3探索三角形全等的条件同步能力提升专题训练 (word解析版)
文档属性
| 名称 | 2021-2022学年苏科版八年级数学上册1.3探索三角形全等的条件同步能力提升专题训练 (word解析版) |
|
|
| 格式 | doc | ||
| 文件大小 | 362.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-22 19:34:38 | ||
图片预览

文档简介
2021-2022学年苏科版八年级数学上册《1.3探索三角形全等的条件》
同步能力提升专题训练(附答案)
1.如图,等腰直角△ABC中,∠BAC=90°,AD⊥BC于D,∠ABC的平分线分别交AC、AD于E、F两点,M为EF的中点,延长AM交BC于点N,连接DM,NE.下列结论:①AE=AF;②AM⊥EF;③△AEF是等边三角形;④DF=DN,⑤AD∥NE.
其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
2.如图,已知等边三角形ABC,点D为线段BC上一点,以线段DB为边向右侧作△DEB,使DE=CD,若∠ADB=m°,∠BDE=(180﹣2m)°,则∠DBE的度数是( )
A.(m﹣60)°
B.(180﹣2m)°
C.(2m﹣90)°
D.(120﹣m)°
3.如图,∠ACB=90°,AC=CD,过点D作AB的垂线交AB的延长线于点E.若AB=2DE,则∠BAC的度数为( )
A.45°
B.30°
C.22.5°
D.15°
4.如图,AD是△ABC的角平分线,∠C=2∠B,F是BC的中点,EF∥AD交AB于点E,且BE=4AE,若CD=4,则AB的长为( )
A.10
B.9
C.8
D.6
5.如图,在Rt△ABC中,∠ACB=90°,BC=5cm,在AC上取一点E,使EC=BC,过点E作EF⊥AC,连接CF,使CF=AB,若EF=12cm,则下列结论不正确的是( )
A.∠F=∠BCF
B.AE=7cm
C.EF平分AB
D.AB⊥CF
6.如图,在四边形ABCD中(AB≠BC),AB∥CD,AB=CD,直线EF经过四边形ABCD的对角线AC和BD的交点O,且分别交AD、BC于点M、N,交BA、DC的延长线于点E、F,下列结论:
①BO=OD;②△AOD的周长﹣△ODC的周长=AD﹣CD;③AD∥BC;④S△ABO=S四边形ABNM;⑤图中全等的三角形的对数是9对;
其中正确结论的个数是( )
A.5
B.4
C.3
D.2
7.下列命题:①有两个角和第三个角的平分线对应相等的两个三角形全等;②有两条边和第三条边上的中线对应相等的两个三角形全等;③有两条边和第三条边上的高对应相等的两个三角形全等.其中正确的是( )
A.①②
B.②③
C.①③
D.①②③
8.如图,方格中△ABC的三个顶点分别在正方形的顶点(格点上),这样的三角形叫格点三角形,图中可以画出与△ABC全等的格点三角形共有( )个.(不含△ABC)
A.28
B.29
C.30
D.31
9.如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能用SAS判定△ABC≌△DEC,能添加的一组条件是( )
A.∠B=∠E,BC=EC
B.∠B=∠E,AC=DC
C.∠A=∠D,BC=EC
D.BC=EC,AC=DC
10.如图,AB⊥CD于点E,且AB=CD=AC,若点I是△ACE的角平分线的交点,点F是BD的中点.下列结论:①∠AIC=135°;②BD=BI;③S△AIC=S△BID;④IF⊥AC.其中正确的是
(填序号).
11.如图,在△ABC中,∠ACB=90°,BC=AC,A
(0,﹣2),C(1,0),点B在第四象限时,则点B的坐标为
.
12.用三角尺可按下面方法画角平分线:在已知∠AOB两边上分别取OM=ON,再分别过点M,N作OA,OB的垂线,两垂线交于点P,画射线OP,则OP平分∠AOB.作图过程用到了△OPM≌△OPN,那么△OPM≌△OPN所用的判定定理是
.
13.如图,在下列条件中,能证明△ABD≌△ACD的是
.(填序号)
①BD=DC,AB=AC;
②∠ADB=∠ADC,BD=DC;
③∠B=∠C,∠BAD=∠CAD;
④∠B=∠C,BD=DC.
14.如图:已知DE=AB,∠D=∠A,请你补充一个条件,使△ABC≌△DEF,并说明你判断的理由:
或
.
15.如图,正方形ABCD的对角线AC,BD交于点O,将一三角尺的直角顶点放在点O处,让其绕点O旋转,三角尺的直角边与正方形ABCD的两边交于点E和F.通过观察或测量OE,OF的长度,你发现了什么?试说明理由.
16.在△ABC和△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.
(1)求证:△ABC≌△DCB;
(2)当∠AEB=50°时,求∠EBC的度数.
17.如图,BD,CE分别是△ABC的高,且BE=CD,求证:Rt△BEC≌Rt△CDB.
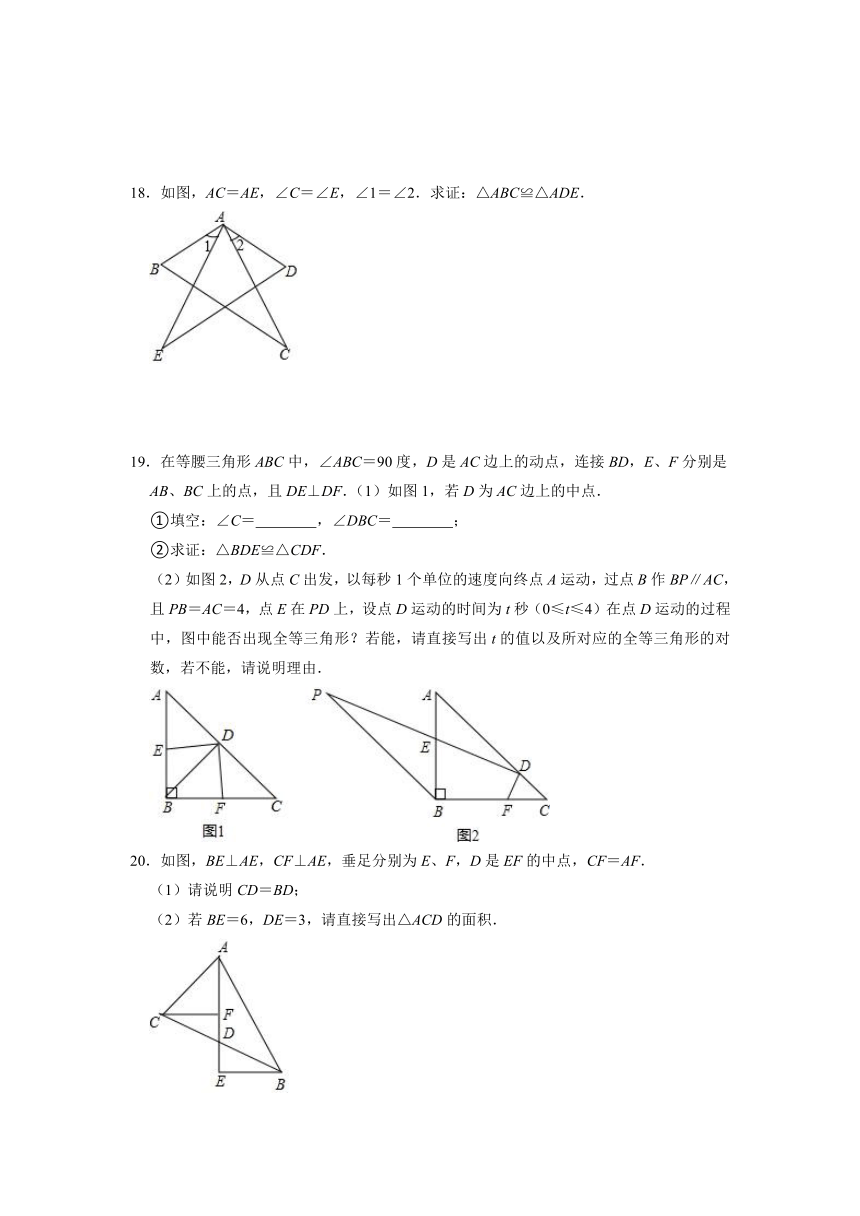
18.如图,AC=AE,∠C=∠E,∠1=∠2.求证:△ABC≌△ADE.
19.在等腰三角形ABC中,∠ABC=90度,D是AC边上的动点,连接BD,E、F分别是AB、BC上的点,且DE⊥DF.(1)如图1,若D为AC边上的中点.
①填空:∠C=
,∠DBC=
;
②求证:△BDE≌△CDF.
(2)如图2,D从点C出发,以每秒1个单位的速度向终点A运动,过点B作BP∥AC,且PB=AC=4,点E在PD上,设点D运动的时间为t秒(0≤t≤4)在点D运动的过程中,图中能否出现全等三角形?若能,请直接写出t的值以及所对应的全等三角形的对数,若不能,请说明理由.
20.如图,BE⊥AE,CF⊥AE,垂足分别为E、F,D是EF的中点,CF=AF.
(1)请说明CD=BD;
(2)若BE=6,DE=3,请直接写出△ACD的面积.
21.如图,AB=AC,AD=AE,∠BAC=∠DAE.
(1)求证:△ABD≌△ACE;
(2)若∠1=25°,∠2=30°,求∠3的度数.
22.如图,△ABC和△EBD中,∠ABC=∠DBE=90°,AB=CB,BE=BD,连接AE,CD,AE与CD交于点M,AE与BC交于点N.
(1)求证:AE=CD;
(2)求证:AE⊥CD;
(3)连接BM,有以下两个结论:①BM平分∠CBE;②MB平分∠AMD.其中正确的有
(请写序号,少选、错选均不得分).
参考答案
1.解:∵∠BAC=90°,AC=AB,AD⊥BC,
∴∠ABC=∠C=45°,AD=BD=CD,∠ADN=∠ADB=90°,
∴∠BAD=45°=∠CAD,
∵BE平分∠ABC,
∴∠ABE=∠CBE=∠ABC=22.5°,
∴∠BFD=∠AEB=90°﹣22.5°=67.5°
∴∠AFE=∠BFD=∠AEB=67.5°,
∴AF=AE,故①正确;③错误,
∵M为EF的中点,
∴AM⊥EF,故②正确;
∵AM⊥EF,
∴∠AMF=∠AME=90°,
∴∠DAN=90°﹣67.5°=22.5°=∠MBN,
在△FBD和△NAD中,
,
∴△FBD≌△NAD(ASA),
∴DF=DN,故④正确;
∵∠BAM=∠BNM=67.5°,
∴BA=BN,
∵∠EBA=∠EBN,BE=BE,
∴△EBA≌△EBN(SAS),
∴∠BNE=∠BAE=90°,
∴∠ENC=∠ADC=90°,
∴AD∥EN.故⑤正确,
故选:D.
2.解:如图,连接AE.
∵△ABC是等边三角形,
∴∠C=∠ABC=60°,
∵∠ADB=m°,∠BDE=(180﹣2m)°,
∴∠ADC=180°﹣m°,∠ADE=180°﹣m°,
∴∠ADC=∠ADE,
∵AD=AD,DC=DE,
∴△ADC≌△ADE(SAS),
∴∠C=∠AED=60°,∠DAC=∠DAE,
∴∠DEA=∠DBA,
∴∠BDE=∠BAE=180°﹣2m,
∵AE=AC=AB,
∴∠ABE=∠AEB=(180°﹣180°+2m)=m,
∴∠DBE=∠ABE﹣∠ABC=(m﹣60)°,
故选:A.
3.解:
连接AD,延长AC、DE交于M,
∵∠ACB=90°,AC=CD,
∴∠DAC=∠ADC=45°,
∵∠ACB=90°,DE⊥AB,
∴∠DEB=90°=∠ACB=∠DCM,
∵∠ABC=∠DBE,
∴由三角形内角和定理得:∠CAB=∠CDM,
在△ACB和△DCM中
∴△ACB≌△DCM(ASA),
∴AB=DM,
∵AB=2DE,
∴DM=2DE,
∴DE=EM,
∵DE⊥AB,
∴AD=AM,
∴∠BAC=∠DAE=∠DAC==22.5°,
故选:C.
4.解:如图作DG⊥AC于G,DH⊥AB于H,在AB上截取AM=AC,
∵DA平分∠BAC,
∴DG=DH,
∴===,
设BF=FC=4a,
∴FD=a,CD=3a=4,
∴a=,BD=5a=,
在△ADM和△ADC中,
,
∴△DAM≌△DAC(SAS),
∴DM=DC,∠AMD=∠C,
∵∠C=2∠B,
∴∠AMD=∠B+∠MDB=2∠B,
∴∠B=∠MDB,
∴BM=MD=CD=4,设AC=AM=x,
∴x=6,
∴AB=BM+AC=4+6=10,
故选:A.
5.解:∵EF⊥AC,
∴∠AEF=∠ACB=90°,
∴EF∥BC,
∴∠F=∠BCF,故A正确;
∵EF⊥AC,
∴∠FEC=∠ACB=90°,
在Rt△ABC和Rt△FEC中,
,
∴Rt△ABC≌Rt△FEC(HL),
∴AC=EF=12cm,
∵CE=BC=5cm,
∴AE=AC﹣CE=7cm.故B正确;
如果AE=CE,
∵EF∥BC,
∴EG是△ABC的中位线,
∴EF平分AB,
而AE与CE不一定相等,
∴不能证明EF平分AB,故C错误;
∵Rt△ABC≌Rt△FEC,
∴∠A=∠F,
∴∠A+∠ACD=∠F+∠ACD=90°,
∴∠ADC=90°,
∴AB⊥CF,故D正确.
∴结论不正确的是C.
故选:C.
6.解:∵AB∥CD,
∴∠ABD=∠CDB,∠BAC=∠DCA,
在△ABO和△CDO中
,
∴△ABO≌△CDO,
∴OB=OD,所以①正确;
OA=OC,
∵△AOD的周长=AD+OA+OD,△ODC的周长=DC+OA+OC,
∴△AOD的周长﹣△ODC的周长=AD﹣DC,所以②正确;
在△ADO和△CBO中
,
∴△ADO≌△CBO,
∴∠DAO=∠BCO,
∴AD∥BC,所以③正确;
易证△AMO≌△CNO,
∴S△AMO=S△CNO,
∴S四边形ABNM=S△ABC,
∵OA=OC,即OA=AC,
∴S△ABO=S△ABC,
∴S△ABO=S四边形ABNM,所以④正确;
图中全等的三角形有:△AOB≌△COD,△AOD≌△COB,△AOM≌△CON,△AOE≌△COF,△MOD≌△NOB,△ABD≌△CDB,△ABC≌△CAD,△AEM≌△CFN,△BOE≌△DOF,
△BNE≌△DMF,所以⑤错误.
故选:B.
7.解:①正确.可以用AAS或者ASA判定两个三角形全等;
②正确.可以用“倍长中线法”,用SAS定理,判断两个三角形全等;
如图,分别延长AD,A′D′到E,E′,使得AD=DE,A′D′=D′E′,
∴△ADC≌△EDB,
∴BE=AC,
同理:B′E′=A′C′,
∴BE=B′E′,AE=A′E′,
∴△ABE≌△A′B′E′,
∴∠BAE=∠B′A′E′,∠E=∠E′,
∴∠CAD=∠C′A′D′,
∴∠BAC=∠B′A′C′,
∴△BAC≌△B′A′C′.
③不正确.因为这个高可能在三角形的内部,也有可能在三角形的外部,也就是说,这两个三角形可能一个是锐角三角形,一个是钝角三角形,所以就不全等了.
故选:A.
8.解:当点B在下面时,根据平移,对称,可得与△ABC全等的三角形有8个,包括△ABC,
当点B在其它3条边上时,有3×8=24(个)三角形与△ABC全等,
∴一共有:8+24﹣1=31(个)三角形与△ABC全等,
故选:D.
9.解:A、若AB=DE,∠B=∠E,BC=EC,符合全等三角形的判定定理SAS,能推出△ABC≌△DEC,故符合题意.
B、若AB=DE,AC=DC,∠B=∠E,由SSA不能判定△ABC≌△DEC,故不符合题意;
C、若AB=DE,BC=EC,∠A=∠D,由SSA不能判定△ABC≌△DEC,故不符合题意;
D、若AB=DE,BC=EC,AC=DC,由SSS不能判定△ABC≌△DEC,故不符合题意;
故选:A.
10.解:如图,延长IF到G,使得FG=FI,连接DG,BG,延长FI交AC于K.
∵AB⊥CD,
∴∠AEC=90°,
∴∠EAC+∠ECA=90°,
∴∠IAC+∠ICA=∠EAC+∠ECA=45°,
∴∠AIC=180°﹣45°=135°,故①正确,
∵AB=AC,∠IAB=∠IAC,AI=AI,
∴△AIB≌△AIC(SAS),
∴∠AIB=∠AIC=135°,IA=ID,
∴∠BIC=360°﹣135°﹣135°=90°,
同法可证:△ICA≌△ICD(SAS),
∴∠AIC=∠CID=135°,IA=ID,
∴∠AID=360°﹣135°﹣135°=90°,
∴∠DIB+∠AIC=180°,
∵DF=FB,IF=FG,
∴四边形IBGD是平行四边形,
∴ID=BG=AI,ID∥BG,
∴∠DIB+∠IBG=180°,
∴∠AIC=∠IBG,
∵IA=ID,IC=IB,
∴△AIC≌△GBI(SAS),
∴∠GIB=∠ACI,S△AIC=S△BGI=S平行四边形DGBI=S△BDI,故③正确,
∵∠GIB+∠CIK=90°,
∴∠CIK+∠ICK=90°,
∴∠IKC=90°,即IF⊥AC,故④正确,
不妨设BI=BD,则△BDI是等腰直角三角形,显然ID=IB,即AI=IC,显然题目不满足这个条件,故②错误.
故答案为①③④.
11.解:过B作BD⊥x轴,垂足为D,
∵∠AOC=∠ACB=90°,
∴∠OAC+∠ACO=∠DCB+∠ACO=90°,
∴∠OAC=∠DCB,
∵AC=BC,
∴△OAC≌△DCB(AAS),
∴OC=BD,OA=CD,
∵A
(0,﹣2),C(1,0),
∴OA=2,OC=1,
∴CD=2,BD=1,
∴OD=3,
∵B点在第四象限,
∴B(3,﹣1).
故答案为(3,﹣1).
12.解:∵OM=ON,OP=OP,∠OMP=∠ONP=90°
∴△OPM≌△OPN
所用的判定定理是HL.
13.解:①②③,
理由是:①∵在△ABD和△ACD中
∴△ABD≌△ACD(SSS);
②∵在△ABD和△ACD中
∴△ABD≌△ACD(SAS);
③∵在△ABD和△ACD中
∴△ABD≌△ACD(AAS);
④连接BC,
∵BD=DC,
∴∠DBC=∠DCB,
∵∠ABD=∠ACD,
∴∠ABC=∠ACB,
∴AB=AC,
在△ABD和△ACD中
∴△ABD≌△ACD(SAS),
故答案为:①②③④.
14.解:∵已知DE=AB,∠D=∠A,
∴根据ASA判断全等添加∠B=∠E;
根据AAS判断全等添加∠ACB=∠DFE;
根据SAS判断全等添加AF=CD.
故填空答案:∠B=∠E或∠ACB=∠DFE或AF=CD.
15.解:OE=OF.
证明:正方形ABCD的对角线AC,BD交于点O,
∴OA=OB,∠OAB=∠OBE=45°,AC⊥BD.
∵∠AOF+∠FOB=∠EOB+∠FOB=90°,
∴∠AOF=∠EOB.
在△AOF和△BOE中
∠OAB=∠OBE,OA=OB,∠AOF=∠EOB,
∴△AOF≌△BOE(ASA).
∴OE=OF.
16.(1)证明:在△ABE和△DCE中,
,
∴△ABE≌△DCE(AAS),
∴AE=DE,BE=CE,
∴AC=DB,
在△ABC和△DCB中,
,
∴△ABC≌△DCB(SAS);
(2)解:∵△ABC≌△DCB,
∴∠ACB=∠DBC,
∵∠AEB=∠ECB+∠EBC=50°,
∴∠EBC=25°.
17.证明:∵BD,CE分别是△ABC的高,
∴∠BEC=∠CDB=90°,
在Rt△BEC和Rt△CDB中,
,
∴Rt△BEC≌Rt△CDB(HL).
18.证明:∵∠1=∠2,
∴∠1+∠EAC=∠2+∠EAC,
∴∠BAC=∠DAE,
在△ABC和△ADE中
∴△ABC≌△ADE(ASA).
19.(1)①解:∵在等腰三角形ABC中,∠ABC=90度,D为AC边上的中点,
∴∠C=45°,∠DBC=45°;
故答案为:45°;45°;
②证明:在等腰直角三角形ABC中,∠ABC=90°,D为AC边上的中点,
故BD⊥AC,
∵ED⊥DF,
∴∠BDE=∠FDC,
∴∠C=∠DBC=45°,
∴BD=DC,
在△BDE和△CDF中,
,
∴△BDE≌△CDF(ASA);
(2)解:如图①所示:当t=0时,△PBE≌△CAE一对;
如图②所示:当t=2时,△AED≌△BFD,△ABD≌△CBD,△BED≌△CFD共3对;
如图③所示:当t=4时,△PBA≌△CAB一对.
20.解:(1)∵BE⊥AE,CF⊥AE,
∴∠BED=∠CFD,
∵D是EF的中点,
∴ED=FD,
在△BED与△CFD中,
,
∴△BED≌△CFD(ASA),
∴CD=BD;
(2)由(1)得:CF=EB=6,
∵AF=CF,
∴AF=6,
∵D是EF的中点,
∴DF=DE=3,
∴AD=9,
∴△ACD的面积:AD?CF=×9×6=27.
21.(1)证明:∵∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠1=∠EAC,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS);
(2)解:∵△ABD≌△ACE,
∴∠ABD=∠2=30°,
∵∠1=25°,
∴∠3=∠1+∠ABD=25°+30°=55°.
22.(1)证明:∵∠ABC=∠DBE,
∴∠ABC+∠CBE=∠DBE+∠CBE,
即∠ABE=∠CBD,
在△ABE和△CBD中,
,
∴△ABE≌△CBD,
∴AE=CD.
(2)∵△ABE≌△CBD,
∴∠BAE=∠BCD,
∵∠NMC=180°﹣∠BCD﹣∠CNM,∠ABC=180°﹣∠BAE﹣∠ANB,
又∠CNM=∠ANB,
∵∠ABC=90°,
∴∠NMC=90°,
∴AE⊥CD.
(3)结论:②
理由:作BK⊥AE于K,BJ⊥CD于J.
∵△ABE≌△CBD,
∴AE=CD,S△ABE=S△CDB,
∴?AE?BK=?CD?BJ,
∴BK=BJ,∵作BK⊥AE于K,BJ⊥CD于J,
∴BM平分∠AMD.
不妨设①成立,则△CBM≌△EBM,则AB=BD,显然不可能,故①错误.
故答案为②.
同步能力提升专题训练(附答案)
1.如图,等腰直角△ABC中,∠BAC=90°,AD⊥BC于D,∠ABC的平分线分别交AC、AD于E、F两点,M为EF的中点,延长AM交BC于点N,连接DM,NE.下列结论:①AE=AF;②AM⊥EF;③△AEF是等边三角形;④DF=DN,⑤AD∥NE.
其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
2.如图,已知等边三角形ABC,点D为线段BC上一点,以线段DB为边向右侧作△DEB,使DE=CD,若∠ADB=m°,∠BDE=(180﹣2m)°,则∠DBE的度数是( )
A.(m﹣60)°
B.(180﹣2m)°
C.(2m﹣90)°
D.(120﹣m)°
3.如图,∠ACB=90°,AC=CD,过点D作AB的垂线交AB的延长线于点E.若AB=2DE,则∠BAC的度数为( )
A.45°
B.30°
C.22.5°
D.15°
4.如图,AD是△ABC的角平分线,∠C=2∠B,F是BC的中点,EF∥AD交AB于点E,且BE=4AE,若CD=4,则AB的长为( )
A.10
B.9
C.8
D.6
5.如图,在Rt△ABC中,∠ACB=90°,BC=5cm,在AC上取一点E,使EC=BC,过点E作EF⊥AC,连接CF,使CF=AB,若EF=12cm,则下列结论不正确的是( )
A.∠F=∠BCF
B.AE=7cm
C.EF平分AB
D.AB⊥CF
6.如图,在四边形ABCD中(AB≠BC),AB∥CD,AB=CD,直线EF经过四边形ABCD的对角线AC和BD的交点O,且分别交AD、BC于点M、N,交BA、DC的延长线于点E、F,下列结论:
①BO=OD;②△AOD的周长﹣△ODC的周长=AD﹣CD;③AD∥BC;④S△ABO=S四边形ABNM;⑤图中全等的三角形的对数是9对;
其中正确结论的个数是( )
A.5
B.4
C.3
D.2
7.下列命题:①有两个角和第三个角的平分线对应相等的两个三角形全等;②有两条边和第三条边上的中线对应相等的两个三角形全等;③有两条边和第三条边上的高对应相等的两个三角形全等.其中正确的是( )
A.①②
B.②③
C.①③
D.①②③
8.如图,方格中△ABC的三个顶点分别在正方形的顶点(格点上),这样的三角形叫格点三角形,图中可以画出与△ABC全等的格点三角形共有( )个.(不含△ABC)
A.28
B.29
C.30
D.31
9.如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能用SAS判定△ABC≌△DEC,能添加的一组条件是( )
A.∠B=∠E,BC=EC
B.∠B=∠E,AC=DC
C.∠A=∠D,BC=EC
D.BC=EC,AC=DC
10.如图,AB⊥CD于点E,且AB=CD=AC,若点I是△ACE的角平分线的交点,点F是BD的中点.下列结论:①∠AIC=135°;②BD=BI;③S△AIC=S△BID;④IF⊥AC.其中正确的是
(填序号).
11.如图,在△ABC中,∠ACB=90°,BC=AC,A
(0,﹣2),C(1,0),点B在第四象限时,则点B的坐标为
.
12.用三角尺可按下面方法画角平分线:在已知∠AOB两边上分别取OM=ON,再分别过点M,N作OA,OB的垂线,两垂线交于点P,画射线OP,则OP平分∠AOB.作图过程用到了△OPM≌△OPN,那么△OPM≌△OPN所用的判定定理是
.
13.如图,在下列条件中,能证明△ABD≌△ACD的是
.(填序号)
①BD=DC,AB=AC;
②∠ADB=∠ADC,BD=DC;
③∠B=∠C,∠BAD=∠CAD;
④∠B=∠C,BD=DC.
14.如图:已知DE=AB,∠D=∠A,请你补充一个条件,使△ABC≌△DEF,并说明你判断的理由:
或
.
15.如图,正方形ABCD的对角线AC,BD交于点O,将一三角尺的直角顶点放在点O处,让其绕点O旋转,三角尺的直角边与正方形ABCD的两边交于点E和F.通过观察或测量OE,OF的长度,你发现了什么?试说明理由.
16.在△ABC和△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.
(1)求证:△ABC≌△DCB;
(2)当∠AEB=50°时,求∠EBC的度数.
17.如图,BD,CE分别是△ABC的高,且BE=CD,求证:Rt△BEC≌Rt△CDB.
18.如图,AC=AE,∠C=∠E,∠1=∠2.求证:△ABC≌△ADE.
19.在等腰三角形ABC中,∠ABC=90度,D是AC边上的动点,连接BD,E、F分别是AB、BC上的点,且DE⊥DF.(1)如图1,若D为AC边上的中点.
①填空:∠C=
,∠DBC=
;
②求证:△BDE≌△CDF.
(2)如图2,D从点C出发,以每秒1个单位的速度向终点A运动,过点B作BP∥AC,且PB=AC=4,点E在PD上,设点D运动的时间为t秒(0≤t≤4)在点D运动的过程中,图中能否出现全等三角形?若能,请直接写出t的值以及所对应的全等三角形的对数,若不能,请说明理由.
20.如图,BE⊥AE,CF⊥AE,垂足分别为E、F,D是EF的中点,CF=AF.
(1)请说明CD=BD;
(2)若BE=6,DE=3,请直接写出△ACD的面积.
21.如图,AB=AC,AD=AE,∠BAC=∠DAE.
(1)求证:△ABD≌△ACE;
(2)若∠1=25°,∠2=30°,求∠3的度数.
22.如图,△ABC和△EBD中,∠ABC=∠DBE=90°,AB=CB,BE=BD,连接AE,CD,AE与CD交于点M,AE与BC交于点N.
(1)求证:AE=CD;
(2)求证:AE⊥CD;
(3)连接BM,有以下两个结论:①BM平分∠CBE;②MB平分∠AMD.其中正确的有
(请写序号,少选、错选均不得分).
参考答案
1.解:∵∠BAC=90°,AC=AB,AD⊥BC,
∴∠ABC=∠C=45°,AD=BD=CD,∠ADN=∠ADB=90°,
∴∠BAD=45°=∠CAD,
∵BE平分∠ABC,
∴∠ABE=∠CBE=∠ABC=22.5°,
∴∠BFD=∠AEB=90°﹣22.5°=67.5°
∴∠AFE=∠BFD=∠AEB=67.5°,
∴AF=AE,故①正确;③错误,
∵M为EF的中点,
∴AM⊥EF,故②正确;
∵AM⊥EF,
∴∠AMF=∠AME=90°,
∴∠DAN=90°﹣67.5°=22.5°=∠MBN,
在△FBD和△NAD中,
,
∴△FBD≌△NAD(ASA),
∴DF=DN,故④正确;
∵∠BAM=∠BNM=67.5°,
∴BA=BN,
∵∠EBA=∠EBN,BE=BE,
∴△EBA≌△EBN(SAS),
∴∠BNE=∠BAE=90°,
∴∠ENC=∠ADC=90°,
∴AD∥EN.故⑤正确,
故选:D.
2.解:如图,连接AE.
∵△ABC是等边三角形,
∴∠C=∠ABC=60°,
∵∠ADB=m°,∠BDE=(180﹣2m)°,
∴∠ADC=180°﹣m°,∠ADE=180°﹣m°,
∴∠ADC=∠ADE,
∵AD=AD,DC=DE,
∴△ADC≌△ADE(SAS),
∴∠C=∠AED=60°,∠DAC=∠DAE,
∴∠DEA=∠DBA,
∴∠BDE=∠BAE=180°﹣2m,
∵AE=AC=AB,
∴∠ABE=∠AEB=(180°﹣180°+2m)=m,
∴∠DBE=∠ABE﹣∠ABC=(m﹣60)°,
故选:A.
3.解:
连接AD,延长AC、DE交于M,
∵∠ACB=90°,AC=CD,
∴∠DAC=∠ADC=45°,
∵∠ACB=90°,DE⊥AB,
∴∠DEB=90°=∠ACB=∠DCM,
∵∠ABC=∠DBE,
∴由三角形内角和定理得:∠CAB=∠CDM,
在△ACB和△DCM中
∴△ACB≌△DCM(ASA),
∴AB=DM,
∵AB=2DE,
∴DM=2DE,
∴DE=EM,
∵DE⊥AB,
∴AD=AM,
∴∠BAC=∠DAE=∠DAC==22.5°,
故选:C.
4.解:如图作DG⊥AC于G,DH⊥AB于H,在AB上截取AM=AC,
∵DA平分∠BAC,
∴DG=DH,
∴===,
设BF=FC=4a,
∴FD=a,CD=3a=4,
∴a=,BD=5a=,
在△ADM和△ADC中,
,
∴△DAM≌△DAC(SAS),
∴DM=DC,∠AMD=∠C,
∵∠C=2∠B,
∴∠AMD=∠B+∠MDB=2∠B,
∴∠B=∠MDB,
∴BM=MD=CD=4,设AC=AM=x,
∴x=6,
∴AB=BM+AC=4+6=10,
故选:A.
5.解:∵EF⊥AC,
∴∠AEF=∠ACB=90°,
∴EF∥BC,
∴∠F=∠BCF,故A正确;
∵EF⊥AC,
∴∠FEC=∠ACB=90°,
在Rt△ABC和Rt△FEC中,
,
∴Rt△ABC≌Rt△FEC(HL),
∴AC=EF=12cm,
∵CE=BC=5cm,
∴AE=AC﹣CE=7cm.故B正确;
如果AE=CE,
∵EF∥BC,
∴EG是△ABC的中位线,
∴EF平分AB,
而AE与CE不一定相等,
∴不能证明EF平分AB,故C错误;
∵Rt△ABC≌Rt△FEC,
∴∠A=∠F,
∴∠A+∠ACD=∠F+∠ACD=90°,
∴∠ADC=90°,
∴AB⊥CF,故D正确.
∴结论不正确的是C.
故选:C.
6.解:∵AB∥CD,
∴∠ABD=∠CDB,∠BAC=∠DCA,
在△ABO和△CDO中
,
∴△ABO≌△CDO,
∴OB=OD,所以①正确;
OA=OC,
∵△AOD的周长=AD+OA+OD,△ODC的周长=DC+OA+OC,
∴△AOD的周长﹣△ODC的周长=AD﹣DC,所以②正确;
在△ADO和△CBO中
,
∴△ADO≌△CBO,
∴∠DAO=∠BCO,
∴AD∥BC,所以③正确;
易证△AMO≌△CNO,
∴S△AMO=S△CNO,
∴S四边形ABNM=S△ABC,
∵OA=OC,即OA=AC,
∴S△ABO=S△ABC,
∴S△ABO=S四边形ABNM,所以④正确;
图中全等的三角形有:△AOB≌△COD,△AOD≌△COB,△AOM≌△CON,△AOE≌△COF,△MOD≌△NOB,△ABD≌△CDB,△ABC≌△CAD,△AEM≌△CFN,△BOE≌△DOF,
△BNE≌△DMF,所以⑤错误.
故选:B.
7.解:①正确.可以用AAS或者ASA判定两个三角形全等;
②正确.可以用“倍长中线法”,用SAS定理,判断两个三角形全等;
如图,分别延长AD,A′D′到E,E′,使得AD=DE,A′D′=D′E′,
∴△ADC≌△EDB,
∴BE=AC,
同理:B′E′=A′C′,
∴BE=B′E′,AE=A′E′,
∴△ABE≌△A′B′E′,
∴∠BAE=∠B′A′E′,∠E=∠E′,
∴∠CAD=∠C′A′D′,
∴∠BAC=∠B′A′C′,
∴△BAC≌△B′A′C′.
③不正确.因为这个高可能在三角形的内部,也有可能在三角形的外部,也就是说,这两个三角形可能一个是锐角三角形,一个是钝角三角形,所以就不全等了.
故选:A.
8.解:当点B在下面时,根据平移,对称,可得与△ABC全等的三角形有8个,包括△ABC,
当点B在其它3条边上时,有3×8=24(个)三角形与△ABC全等,
∴一共有:8+24﹣1=31(个)三角形与△ABC全等,
故选:D.
9.解:A、若AB=DE,∠B=∠E,BC=EC,符合全等三角形的判定定理SAS,能推出△ABC≌△DEC,故符合题意.
B、若AB=DE,AC=DC,∠B=∠E,由SSA不能判定△ABC≌△DEC,故不符合题意;
C、若AB=DE,BC=EC,∠A=∠D,由SSA不能判定△ABC≌△DEC,故不符合题意;
D、若AB=DE,BC=EC,AC=DC,由SSS不能判定△ABC≌△DEC,故不符合题意;
故选:A.
10.解:如图,延长IF到G,使得FG=FI,连接DG,BG,延长FI交AC于K.
∵AB⊥CD,
∴∠AEC=90°,
∴∠EAC+∠ECA=90°,
∴∠IAC+∠ICA=∠EAC+∠ECA=45°,
∴∠AIC=180°﹣45°=135°,故①正确,
∵AB=AC,∠IAB=∠IAC,AI=AI,
∴△AIB≌△AIC(SAS),
∴∠AIB=∠AIC=135°,IA=ID,
∴∠BIC=360°﹣135°﹣135°=90°,
同法可证:△ICA≌△ICD(SAS),
∴∠AIC=∠CID=135°,IA=ID,
∴∠AID=360°﹣135°﹣135°=90°,
∴∠DIB+∠AIC=180°,
∵DF=FB,IF=FG,
∴四边形IBGD是平行四边形,
∴ID=BG=AI,ID∥BG,
∴∠DIB+∠IBG=180°,
∴∠AIC=∠IBG,
∵IA=ID,IC=IB,
∴△AIC≌△GBI(SAS),
∴∠GIB=∠ACI,S△AIC=S△BGI=S平行四边形DGBI=S△BDI,故③正确,
∵∠GIB+∠CIK=90°,
∴∠CIK+∠ICK=90°,
∴∠IKC=90°,即IF⊥AC,故④正确,
不妨设BI=BD,则△BDI是等腰直角三角形,显然ID=IB,即AI=IC,显然题目不满足这个条件,故②错误.
故答案为①③④.
11.解:过B作BD⊥x轴,垂足为D,
∵∠AOC=∠ACB=90°,
∴∠OAC+∠ACO=∠DCB+∠ACO=90°,
∴∠OAC=∠DCB,
∵AC=BC,
∴△OAC≌△DCB(AAS),
∴OC=BD,OA=CD,
∵A
(0,﹣2),C(1,0),
∴OA=2,OC=1,
∴CD=2,BD=1,
∴OD=3,
∵B点在第四象限,
∴B(3,﹣1).
故答案为(3,﹣1).
12.解:∵OM=ON,OP=OP,∠OMP=∠ONP=90°
∴△OPM≌△OPN
所用的判定定理是HL.
13.解:①②③,
理由是:①∵在△ABD和△ACD中
∴△ABD≌△ACD(SSS);
②∵在△ABD和△ACD中
∴△ABD≌△ACD(SAS);
③∵在△ABD和△ACD中
∴△ABD≌△ACD(AAS);
④连接BC,
∵BD=DC,
∴∠DBC=∠DCB,
∵∠ABD=∠ACD,
∴∠ABC=∠ACB,
∴AB=AC,
在△ABD和△ACD中
∴△ABD≌△ACD(SAS),
故答案为:①②③④.
14.解:∵已知DE=AB,∠D=∠A,
∴根据ASA判断全等添加∠B=∠E;
根据AAS判断全等添加∠ACB=∠DFE;
根据SAS判断全等添加AF=CD.
故填空答案:∠B=∠E或∠ACB=∠DFE或AF=CD.
15.解:OE=OF.
证明:正方形ABCD的对角线AC,BD交于点O,
∴OA=OB,∠OAB=∠OBE=45°,AC⊥BD.
∵∠AOF+∠FOB=∠EOB+∠FOB=90°,
∴∠AOF=∠EOB.
在△AOF和△BOE中
∠OAB=∠OBE,OA=OB,∠AOF=∠EOB,
∴△AOF≌△BOE(ASA).
∴OE=OF.
16.(1)证明:在△ABE和△DCE中,
,
∴△ABE≌△DCE(AAS),
∴AE=DE,BE=CE,
∴AC=DB,
在△ABC和△DCB中,
,
∴△ABC≌△DCB(SAS);
(2)解:∵△ABC≌△DCB,
∴∠ACB=∠DBC,
∵∠AEB=∠ECB+∠EBC=50°,
∴∠EBC=25°.
17.证明:∵BD,CE分别是△ABC的高,
∴∠BEC=∠CDB=90°,
在Rt△BEC和Rt△CDB中,
,
∴Rt△BEC≌Rt△CDB(HL).
18.证明:∵∠1=∠2,
∴∠1+∠EAC=∠2+∠EAC,
∴∠BAC=∠DAE,
在△ABC和△ADE中
∴△ABC≌△ADE(ASA).
19.(1)①解:∵在等腰三角形ABC中,∠ABC=90度,D为AC边上的中点,
∴∠C=45°,∠DBC=45°;
故答案为:45°;45°;
②证明:在等腰直角三角形ABC中,∠ABC=90°,D为AC边上的中点,
故BD⊥AC,
∵ED⊥DF,
∴∠BDE=∠FDC,
∴∠C=∠DBC=45°,
∴BD=DC,
在△BDE和△CDF中,
,
∴△BDE≌△CDF(ASA);
(2)解:如图①所示:当t=0时,△PBE≌△CAE一对;
如图②所示:当t=2时,△AED≌△BFD,△ABD≌△CBD,△BED≌△CFD共3对;
如图③所示:当t=4时,△PBA≌△CAB一对.
20.解:(1)∵BE⊥AE,CF⊥AE,
∴∠BED=∠CFD,
∵D是EF的中点,
∴ED=FD,
在△BED与△CFD中,
,
∴△BED≌△CFD(ASA),
∴CD=BD;
(2)由(1)得:CF=EB=6,
∵AF=CF,
∴AF=6,
∵D是EF的中点,
∴DF=DE=3,
∴AD=9,
∴△ACD的面积:AD?CF=×9×6=27.
21.(1)证明:∵∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠1=∠EAC,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS);
(2)解:∵△ABD≌△ACE,
∴∠ABD=∠2=30°,
∵∠1=25°,
∴∠3=∠1+∠ABD=25°+30°=55°.
22.(1)证明:∵∠ABC=∠DBE,
∴∠ABC+∠CBE=∠DBE+∠CBE,
即∠ABE=∠CBD,
在△ABE和△CBD中,
,
∴△ABE≌△CBD,
∴AE=CD.
(2)∵△ABE≌△CBD,
∴∠BAE=∠BCD,
∵∠NMC=180°﹣∠BCD﹣∠CNM,∠ABC=180°﹣∠BAE﹣∠ANB,
又∠CNM=∠ANB,
∵∠ABC=90°,
∴∠NMC=90°,
∴AE⊥CD.
(3)结论:②
理由:作BK⊥AE于K,BJ⊥CD于J.
∵△ABE≌△CBD,
∴AE=CD,S△ABE=S△CDB,
∴?AE?BK=?CD?BJ,
∴BK=BJ,∵作BK⊥AE于K,BJ⊥CD于J,
∴BM平分∠AMD.
不妨设①成立,则△CBM≌△EBM,则AB=BD,显然不可能,故①错误.
故答案为②.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
