2021-2022学年九年级数学苏科版上册 2.7弧长及扇形面积 同步练习题(word版含解析)
文档属性
| 名称 | 2021-2022学年九年级数学苏科版上册 2.7弧长及扇形面积 同步练习题(word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 383.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-22 23:19:20 | ||
图片预览

文档简介
2021-2022学年苏科版九年级数学上册《2.7弧长及扇形面积》同步练习题(附答案)
1.已知扇形的半径为6,圆心角为150°,则它的面积是( )
A.π
B.3π
C.5π
D.15π
2.如图古希腊数学家希波克拉底所研究的几何图形,此图由三个半圆构成,三个半圆的直径分别为直角三角形ABC的斜边BC,直角边AB,AC.若△ABC的三边所围成的区域面积记为S1,黑色部分面积记为S2,其余部分面积记为S3,则下列关系式正确的是( )
A.S1=S2
B.S2=S3
C.S2+S3=S1
D.S22+S32=S12
3.已知一个扇形的圆心角为120°,半径为4,则该扇形的弧长为( )
A.2π
B.π
C.3π
D.π
4.如图,AB⊥OB,AB=2,OB=4,把∠ABO绕点O顺时针旋转60°得∠CDO,则AB扫过的面积(图中阴影部分)为( )
A.2
B.2π
C.
D.π
5.如图,两个半径长均为的直角扇形的圆心分别在对方的圆弧上,扇形CFD的圆心C是的中点,且扇形CFD绕着点C旋转,半径AE、CF交于点G,半径BE、CD交于点H,则图中阴影面积等于( )
A.
B.
C.π﹣1
D.π﹣2
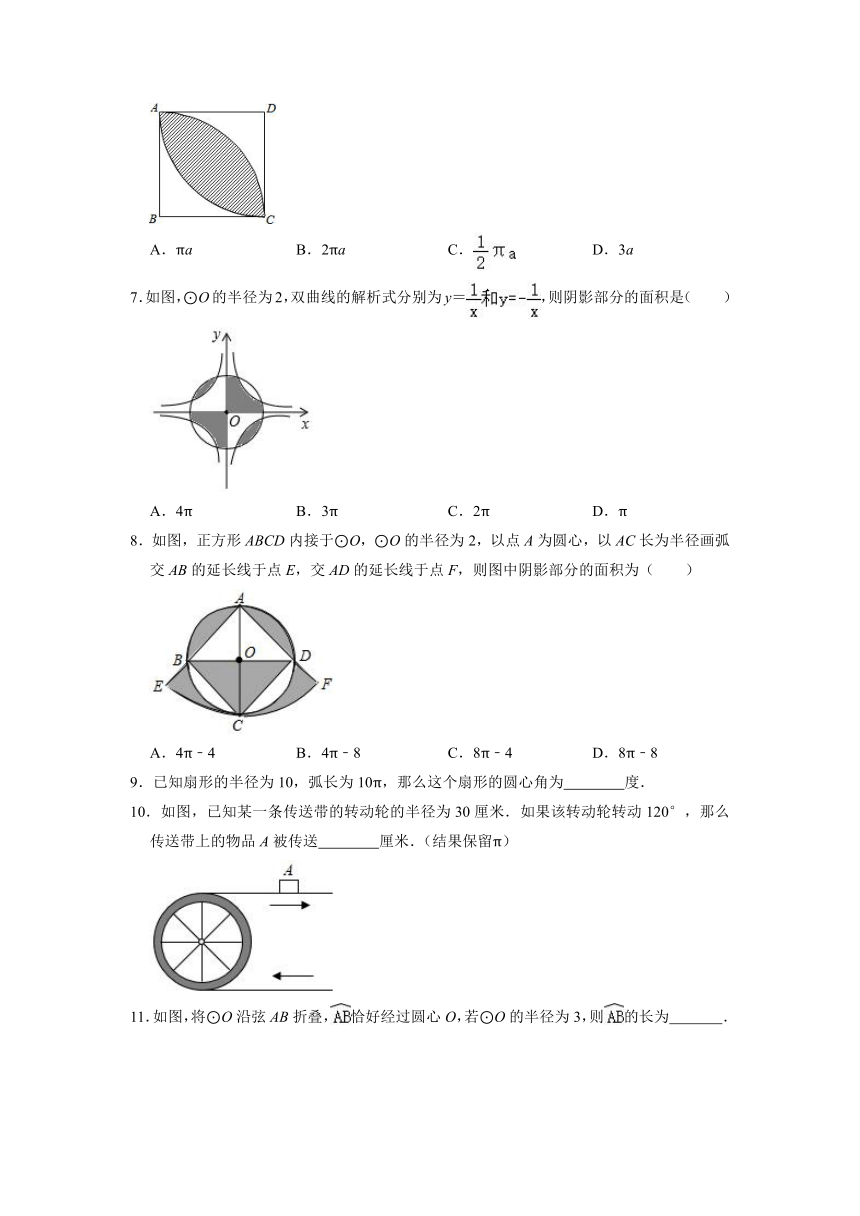
6.如图,正方形ABCD中,分别以B、D为圆心,以正方形的边长a为半径画弧,形成树叶形(阴影部分)图案,则树叶形图案的周长为( )
A.πa
B.2πa
C.
D.3a
7.如图,⊙O的半径为2,双曲线的解析式分别为y=,则阴影部分的面积是( )
A.4π
B.3π
C.2π
D.π
8.如图,正方形ABCD内接于⊙O,⊙O的半径为2,以点A为圆心,以AC长为半径画弧交AB的延长线于点E,交AD的延长线于点F,则图中阴影部分的面积为( )
A.4π﹣4
B.4π﹣8
C.8π﹣4
D.8π﹣8
9.已知扇形的半径为10,弧长为10π,那么这个扇形的圆心角为
度.
10.如图,已知某一条传送带的转动轮的半径为30厘米.如果该转动轮转动120°,那么传送带上的物品A被传送
厘米.(结果保留π)
11.如图,将⊙O沿弦AB折叠,恰好经过圆心O,若⊙O的半径为3,则的长为
.
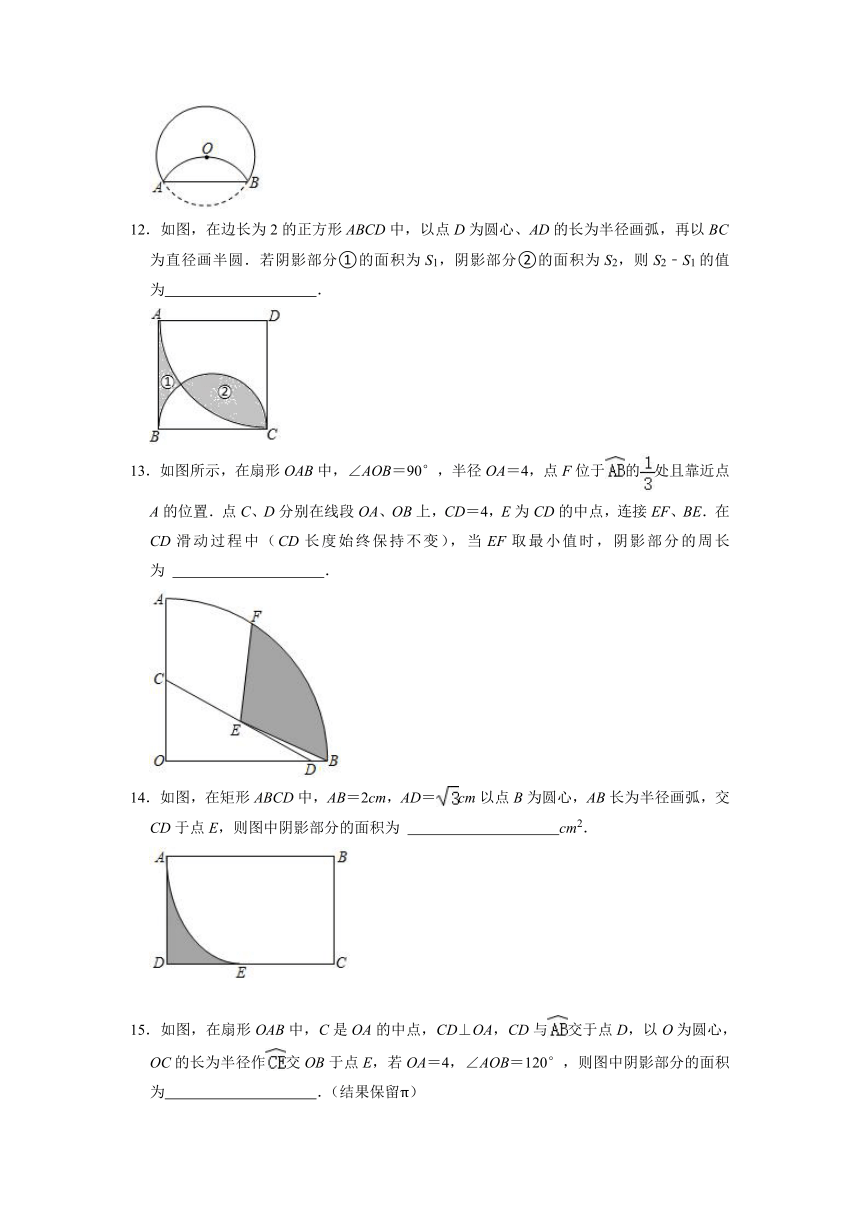
12.如图,在边长为2的正方形ABCD中,以点D为圆心、AD的长为半径画弧,再以BC为直径画半圆.若阴影部分①的面积为S1,阴影部分②的面积为S2,则S2﹣S1的值为
.
13.如图所示,在扇形OAB中,∠AOB=90°,半径OA=4,点F位于的处且靠近点A的位置.点C、D分别在线段OA、OB上,CD=4,E为CD的中点,连接EF、BE.在CD滑动过程中(CD长度始终保持不变),当EF取最小值时,阴影部分的周长为
.
14.如图,在矩形ABCD中,AB=2cm,AD=cm以点B为圆心,AB长为半径画弧,交CD于点E,则图中阴影部分的面积为
cm2.
15.如图,在扇形OAB中,C是OA的中点,CD⊥OA,CD与交于点D,以O为圆心,OC的长为半径作交OB于点E,若OA=4,∠AOB=120°,则图中阴影部分的面积为
.(结果保留π)
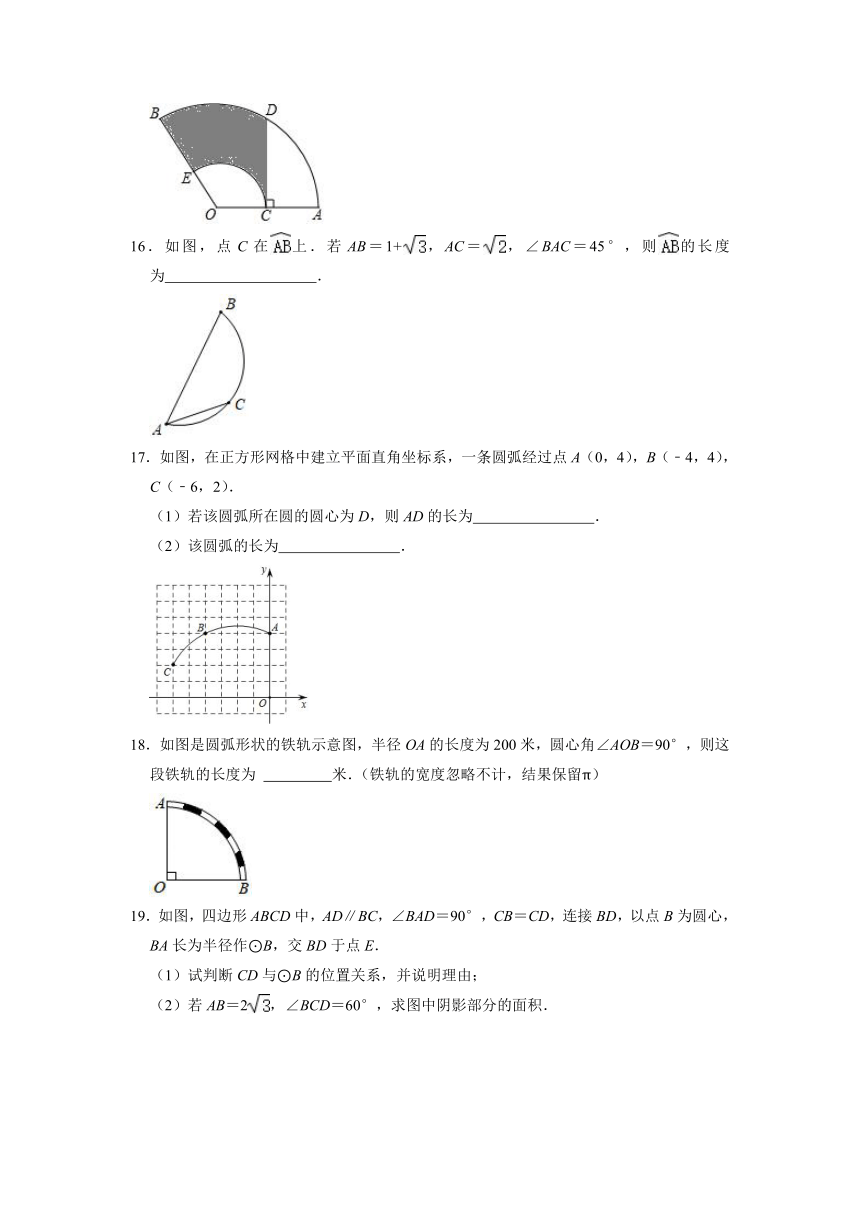
16.如图,点C在上.若AB=1+,AC=,∠BAC=45°,则的长度为
.
17.如图,在正方形网格中建立平面直角坐标系,一条圆弧经过点A(0,4),B(﹣4,4),C(﹣6,2).
(1)若该圆弧所在圆的圆心为D,则AD的长为
.
(2)该圆弧的长为
.
18.如图是圆弧形状的铁轨示意图,半径OA的长度为200米,圆心角∠AOB=90°,则这段铁轨的长度为
米.(铁轨的宽度忽略不计,结果保留π)
19.如图,四边形ABCD中,AD∥BC,∠BAD=90°,CB=CD,连接BD,以点B为圆心,BA长为半径作⊙B,交BD于点E.
(1)试判断CD与⊙B的位置关系,并说明理由;
(2)若AB=2,∠BCD=60°,求图中阴影部分的面积.
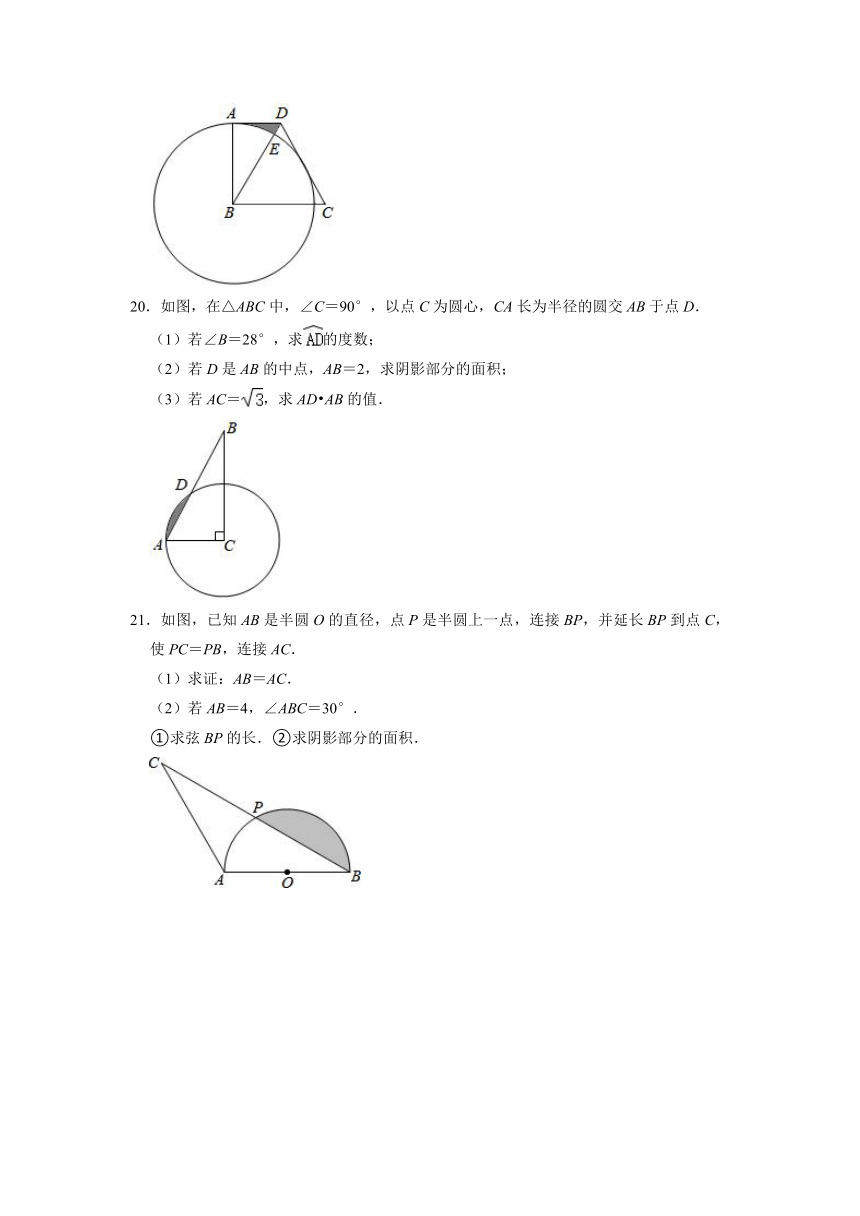
20.如图,在△ABC中,∠C=90°,以点C为圆心,CA长为半径的圆交AB于点D.
(1)若∠B=28°,求的度数;
(2)若D是AB的中点,AB=2,求阴影部分的面积;
(3)若AC=,求AD?AB的值.
21.如图,已知AB是半圆O的直径,点P是半圆上一点,连接BP,并延长BP到点C,使PC=PB,连接AC.
(1)求证:AB=AC.
(2)若AB=4,∠ABC=30°.
①求弦BP的长.②求阴影部分的面积.
参考答案
1.解:扇形面积=,
故选:D.
2.解:设AB=c,AC=b,BC=a,
S3=π?(a)2﹣S1=πa2﹣S1,
S2=π?(c)2+π?(b)2﹣S3=πc2+πb2﹣S3=π(c2+b2)﹣(πa2﹣S1),
∵c2+b2=a2,
∴S2=S1.
故选:A.
3.解:∵一个扇形的圆心角为120°,半径为4,
∴该扇形的弧长为:l==π,
故选:B.
4.解:连接OA、OC,
∵AB⊥OB,AB=2,OB=4,
∴OA=2,
∵AB扫过的面积=S扇形OAC+S△COD﹣S△AOB﹣S扇形OBD,
∵S△COD=S△AOB,
∴边AB扫过的面积=﹣=π,
故选:C.
5.解:两扇形的面积和为:=π,
过点C作CM⊥AE,作CN⊥BE,垂足分别为M、N,
则四边形EMCN是矩形,
∵点C是的中点,
∴EC平分∠AEB,
∴CM=CN,
∴矩形EMCN是正方形,
∵∠MCG+∠FCN=90°,∠NCH+∠FCN=90°,
∴∠MCG=∠NCH,
在△CMG与△CNH中,
,
∴△CMG≌△CNH(ASA),
∴中间空白区域面积相当于对角线是的正方形面积,
∴空白区域的面积为:××=1,
∴图中阴影部分的面积=两个扇形面积和﹣2个空白区域面积的和=π﹣2.
故选:D.
6.解:∵四边形ABCD是边长为a正方形,
∴∠B=∠D=90°,AB=CB=AD=CD=a,
∴树叶形图案的周长=×2=πa.
故选:A.
7.解:双曲线y=的图象关于x轴对称,
根据图形的对称性,把第二象限和第四象限的阴影部分的面积拼到第一和第三象限中的阴影中,可以得到阴影部分就是一个扇形,
并且扇形的圆心角为180°,半径为2,
所以:S阴影==2π.
故选:C.
8.解:利用对称性可知:阴影部分的面积=扇形AEF的面积﹣△ABD的面积=﹣×4×2=4π﹣4,
故选:A.
9.解:由题意可得,
10π=,
解得n=180,
即这个扇形的圆心角为180°,
故答案为:180.
10.解:根据弧长公式可知,
传送带上的物品A被传送的距离为=20π(厘米),
故答案为20π.
11.解:连接OA、OB,作OC⊥AB于C,
由题意得,OC=OA,
∴∠OAC=30°,
∵OA=OB,
∴∠OBA=∠OAC=30°,
∴∠AOB=120°,
∴的长==2π,
故答案为:2π.
12.解:由图形可知,扇形ADC的面积+半圆BC的面积+阴影部分①的面积﹣正方形ABCD的面积=阴影部分②的面积,
∴S2﹣S1=扇形ADC的面积+半圆BC的面积﹣正方形ABCD的面积
=+π×12﹣22
=﹣4,
故答案为:﹣4.
13.解:如图,连接OF,OE,BF,取OF的中点T,连接BT.
∵∠AOB=90°,=,
∴∠BOF=60°,
∴的长==π,
∵CE=DE,
∴OE=CD=2,
∵OF=4,
∴EF≥OF﹣OE=2,
∴当O,E,F共线时,EF的值最小,此时点E与点T重合,
∴此时EF=2,
∵OF=OB,∠BOF=60°,
∴△BOF是等边三角形,
∵OT=TF,
∴BT⊥OF,
∴BE=BT===2,
∴此时阴影部分的周长为2+2+π.
故答案为:2+2+π.
14.解:如图,连接BE.
∵四边形ABCD是矩形,
∴AD=BC=cm,∠C=∠ABC=90°,CD∥AB,
在Rt△BCE中,
∵AB=BE=2cm,BC=cm,
∴EC==1cm,
∴∠EBC=30°,
∴∠ABE=∠BEC=60°,
∴S阴=S矩形ABCD﹣S△BEC﹣S扇形AEB,
=2﹣×1×﹣?π?22,
=(﹣π)cm2.
故答案为:(﹣π).
15.解:如图,连接OD,AD,
∵点C为OA的中点,
∴OC=OA=OD,
∵CD⊥OA,
∴∠CDO=30°,∠DOC=60°,
∴△ADO为等边三角形,
∴CD=2,
∴S扇形AOD==π,
∴S阴影=S扇形AOB﹣S扇形COE﹣(S扇形AOD﹣S△COD)
=﹣﹣(π﹣×2×2)
=π﹣π﹣π+2
=π+2.
故答案为π+2.
16.解:如图,设圆心为O,连接OA,OB,OC,BC,过点C作CT⊥AB于T.
∵∠CTA=90°,∠CAT=45°,AC=,
∴AT=TC=1,
∵AB=1+,
∴BT=,
∴∠CBT=30°,
∴∠AOC=2∠CBT=60°,∠COB=2∠CAB=90°,
∵OA=OC,
∴△AOC是等边三角形,
∴OA=,∠AOB=150°,
∴的长==π,
故答案为:π.
17.解:(1)分别作线段BA和BC的垂直平分线EF、MN,则直线EF和直线MN的交点为D,则D为已知弧的圆心,如图,
∵A(0,4),B(﹣4,4),
∴OA=4,AB=4,
∴OD=2,
在Rt△AOD中,由勾股定理得:AD===2,
故答案为:2;
(2)连接AC、CD,
∵A(0,4),B(﹣4,4),C(﹣6,2),OD=2,
∴由勾股定理得:CD==,AD==,AC==,
∴CD2+AD2=AC2,
∴∠ADC=90°,
∴圆弧的长度是=π.
18.解:圆弧长是:=100π(米).
故答案是:100π.
19.解:(1)过点B作BF⊥CD,垂足为F,
∵AD∥BC,
∴∠ADB=∠CBD,
∵CB=CD,
∴∠CBD=∠CDB,
∴∠ADB=∠CDB.
在△ABD和△FBD中,
,
∴△ABD≌△FBD(AAS),
∴BF=BA,则点F在圆B上,
∴CD与⊙B相切;
(2)∵∠BCD=60°,CB=CD,
∴△BCD是等边三角形,
∴∠CBD=60°
∵BF⊥CD,
∴∠ABD=∠DBF=∠CBF=30°,
∴∠ABF=60°,
∵AB=BF=,
∴AD=DF=AB·tan30°=2,
∴阴影部分的面积=S△ABD﹣S扇形ABE
=
=.
20.解:(1)连接CD,如图,
∵∠ACB=90°,∠B=28°,
∴∠BAC=90°﹣28°=62°,
∵CA=CD,
∴∠CDA=∠CAD=62°,
∴∠ACD=180°﹣62°﹣62°=56°,
∴的度数为56°;
(2)∵D是AB的中点,∠ACB=90°,
∴CD=AD=BD=AB=1,
∵CD=CA,
∴△ACD为等边三角形,
∴∠ACD=60°,
∴阴影部分的面积=S扇形ACD﹣S△ACD
=﹣×12
=π﹣;
(3)过点C作CH⊥AD于H,
∴AH=DH=AD,
∵∠ACB=90°,CH⊥AB,
∴∠ACB=∠AHC,
∵∠A=∠A,
∴△ACH∽△△ABC,
∴AC:AB=AH:AC,
∴AC2=AH?AB,
即()2=AD?AB,
∴AD?AB=6.
21.(1)证明:连接AP,
∵AB是半圆O的直径,
∴∠APB=90°,
∴AP⊥BC.
∵PC=PB,
∴△ABC是等腰三角形,即AB=AC;
(2)解:①∵∠APB=90°,AB=4,∠ABC=30°,
∴AP=AB=2,
∴BP===2;
②连接OP,
∵∠ABC=30°,
∴∠PAB=60°,
∴∠POB=120°.
∵点O是AB的中点,
∴S△POB=S△PAB=×AP?PB=×2×2=,
∴S阴影=S扇形BOP﹣S△POB
=﹣
=π﹣.
1.已知扇形的半径为6,圆心角为150°,则它的面积是( )
A.π
B.3π
C.5π
D.15π
2.如图古希腊数学家希波克拉底所研究的几何图形,此图由三个半圆构成,三个半圆的直径分别为直角三角形ABC的斜边BC,直角边AB,AC.若△ABC的三边所围成的区域面积记为S1,黑色部分面积记为S2,其余部分面积记为S3,则下列关系式正确的是( )
A.S1=S2
B.S2=S3
C.S2+S3=S1
D.S22+S32=S12
3.已知一个扇形的圆心角为120°,半径为4,则该扇形的弧长为( )
A.2π
B.π
C.3π
D.π
4.如图,AB⊥OB,AB=2,OB=4,把∠ABO绕点O顺时针旋转60°得∠CDO,则AB扫过的面积(图中阴影部分)为( )
A.2
B.2π
C.
D.π
5.如图,两个半径长均为的直角扇形的圆心分别在对方的圆弧上,扇形CFD的圆心C是的中点,且扇形CFD绕着点C旋转,半径AE、CF交于点G,半径BE、CD交于点H,则图中阴影面积等于( )
A.
B.
C.π﹣1
D.π﹣2
6.如图,正方形ABCD中,分别以B、D为圆心,以正方形的边长a为半径画弧,形成树叶形(阴影部分)图案,则树叶形图案的周长为( )
A.πa
B.2πa
C.
D.3a
7.如图,⊙O的半径为2,双曲线的解析式分别为y=,则阴影部分的面积是( )
A.4π
B.3π
C.2π
D.π
8.如图,正方形ABCD内接于⊙O,⊙O的半径为2,以点A为圆心,以AC长为半径画弧交AB的延长线于点E,交AD的延长线于点F,则图中阴影部分的面积为( )
A.4π﹣4
B.4π﹣8
C.8π﹣4
D.8π﹣8
9.已知扇形的半径为10,弧长为10π,那么这个扇形的圆心角为
度.
10.如图,已知某一条传送带的转动轮的半径为30厘米.如果该转动轮转动120°,那么传送带上的物品A被传送
厘米.(结果保留π)
11.如图,将⊙O沿弦AB折叠,恰好经过圆心O,若⊙O的半径为3,则的长为
.
12.如图,在边长为2的正方形ABCD中,以点D为圆心、AD的长为半径画弧,再以BC为直径画半圆.若阴影部分①的面积为S1,阴影部分②的面积为S2,则S2﹣S1的值为
.
13.如图所示,在扇形OAB中,∠AOB=90°,半径OA=4,点F位于的处且靠近点A的位置.点C、D分别在线段OA、OB上,CD=4,E为CD的中点,连接EF、BE.在CD滑动过程中(CD长度始终保持不变),当EF取最小值时,阴影部分的周长为
.
14.如图,在矩形ABCD中,AB=2cm,AD=cm以点B为圆心,AB长为半径画弧,交CD于点E,则图中阴影部分的面积为
cm2.
15.如图,在扇形OAB中,C是OA的中点,CD⊥OA,CD与交于点D,以O为圆心,OC的长为半径作交OB于点E,若OA=4,∠AOB=120°,则图中阴影部分的面积为
.(结果保留π)
16.如图,点C在上.若AB=1+,AC=,∠BAC=45°,则的长度为
.
17.如图,在正方形网格中建立平面直角坐标系,一条圆弧经过点A(0,4),B(﹣4,4),C(﹣6,2).
(1)若该圆弧所在圆的圆心为D,则AD的长为
.
(2)该圆弧的长为
.
18.如图是圆弧形状的铁轨示意图,半径OA的长度为200米,圆心角∠AOB=90°,则这段铁轨的长度为
米.(铁轨的宽度忽略不计,结果保留π)
19.如图,四边形ABCD中,AD∥BC,∠BAD=90°,CB=CD,连接BD,以点B为圆心,BA长为半径作⊙B,交BD于点E.
(1)试判断CD与⊙B的位置关系,并说明理由;
(2)若AB=2,∠BCD=60°,求图中阴影部分的面积.
20.如图,在△ABC中,∠C=90°,以点C为圆心,CA长为半径的圆交AB于点D.
(1)若∠B=28°,求的度数;
(2)若D是AB的中点,AB=2,求阴影部分的面积;
(3)若AC=,求AD?AB的值.
21.如图,已知AB是半圆O的直径,点P是半圆上一点,连接BP,并延长BP到点C,使PC=PB,连接AC.
(1)求证:AB=AC.
(2)若AB=4,∠ABC=30°.
①求弦BP的长.②求阴影部分的面积.
参考答案
1.解:扇形面积=,
故选:D.
2.解:设AB=c,AC=b,BC=a,
S3=π?(a)2﹣S1=πa2﹣S1,
S2=π?(c)2+π?(b)2﹣S3=πc2+πb2﹣S3=π(c2+b2)﹣(πa2﹣S1),
∵c2+b2=a2,
∴S2=S1.
故选:A.
3.解:∵一个扇形的圆心角为120°,半径为4,
∴该扇形的弧长为:l==π,
故选:B.
4.解:连接OA、OC,
∵AB⊥OB,AB=2,OB=4,
∴OA=2,
∵AB扫过的面积=S扇形OAC+S△COD﹣S△AOB﹣S扇形OBD,
∵S△COD=S△AOB,
∴边AB扫过的面积=﹣=π,
故选:C.
5.解:两扇形的面积和为:=π,
过点C作CM⊥AE,作CN⊥BE,垂足分别为M、N,
则四边形EMCN是矩形,
∵点C是的中点,
∴EC平分∠AEB,
∴CM=CN,
∴矩形EMCN是正方形,
∵∠MCG+∠FCN=90°,∠NCH+∠FCN=90°,
∴∠MCG=∠NCH,
在△CMG与△CNH中,
,
∴△CMG≌△CNH(ASA),
∴中间空白区域面积相当于对角线是的正方形面积,
∴空白区域的面积为:××=1,
∴图中阴影部分的面积=两个扇形面积和﹣2个空白区域面积的和=π﹣2.
故选:D.
6.解:∵四边形ABCD是边长为a正方形,
∴∠B=∠D=90°,AB=CB=AD=CD=a,
∴树叶形图案的周长=×2=πa.
故选:A.
7.解:双曲线y=的图象关于x轴对称,
根据图形的对称性,把第二象限和第四象限的阴影部分的面积拼到第一和第三象限中的阴影中,可以得到阴影部分就是一个扇形,
并且扇形的圆心角为180°,半径为2,
所以:S阴影==2π.
故选:C.
8.解:利用对称性可知:阴影部分的面积=扇形AEF的面积﹣△ABD的面积=﹣×4×2=4π﹣4,
故选:A.
9.解:由题意可得,
10π=,
解得n=180,
即这个扇形的圆心角为180°,
故答案为:180.
10.解:根据弧长公式可知,
传送带上的物品A被传送的距离为=20π(厘米),
故答案为20π.
11.解:连接OA、OB,作OC⊥AB于C,
由题意得,OC=OA,
∴∠OAC=30°,
∵OA=OB,
∴∠OBA=∠OAC=30°,
∴∠AOB=120°,
∴的长==2π,
故答案为:2π.
12.解:由图形可知,扇形ADC的面积+半圆BC的面积+阴影部分①的面积﹣正方形ABCD的面积=阴影部分②的面积,
∴S2﹣S1=扇形ADC的面积+半圆BC的面积﹣正方形ABCD的面积
=+π×12﹣22
=﹣4,
故答案为:﹣4.
13.解:如图,连接OF,OE,BF,取OF的中点T,连接BT.
∵∠AOB=90°,=,
∴∠BOF=60°,
∴的长==π,
∵CE=DE,
∴OE=CD=2,
∵OF=4,
∴EF≥OF﹣OE=2,
∴当O,E,F共线时,EF的值最小,此时点E与点T重合,
∴此时EF=2,
∵OF=OB,∠BOF=60°,
∴△BOF是等边三角形,
∵OT=TF,
∴BT⊥OF,
∴BE=BT===2,
∴此时阴影部分的周长为2+2+π.
故答案为:2+2+π.
14.解:如图,连接BE.
∵四边形ABCD是矩形,
∴AD=BC=cm,∠C=∠ABC=90°,CD∥AB,
在Rt△BCE中,
∵AB=BE=2cm,BC=cm,
∴EC==1cm,
∴∠EBC=30°,
∴∠ABE=∠BEC=60°,
∴S阴=S矩形ABCD﹣S△BEC﹣S扇形AEB,
=2﹣×1×﹣?π?22,
=(﹣π)cm2.
故答案为:(﹣π).
15.解:如图,连接OD,AD,
∵点C为OA的中点,
∴OC=OA=OD,
∵CD⊥OA,
∴∠CDO=30°,∠DOC=60°,
∴△ADO为等边三角形,
∴CD=2,
∴S扇形AOD==π,
∴S阴影=S扇形AOB﹣S扇形COE﹣(S扇形AOD﹣S△COD)
=﹣﹣(π﹣×2×2)
=π﹣π﹣π+2
=π+2.
故答案为π+2.
16.解:如图,设圆心为O,连接OA,OB,OC,BC,过点C作CT⊥AB于T.
∵∠CTA=90°,∠CAT=45°,AC=,
∴AT=TC=1,
∵AB=1+,
∴BT=,
∴∠CBT=30°,
∴∠AOC=2∠CBT=60°,∠COB=2∠CAB=90°,
∵OA=OC,
∴△AOC是等边三角形,
∴OA=,∠AOB=150°,
∴的长==π,
故答案为:π.
17.解:(1)分别作线段BA和BC的垂直平分线EF、MN,则直线EF和直线MN的交点为D,则D为已知弧的圆心,如图,
∵A(0,4),B(﹣4,4),
∴OA=4,AB=4,
∴OD=2,
在Rt△AOD中,由勾股定理得:AD===2,
故答案为:2;
(2)连接AC、CD,
∵A(0,4),B(﹣4,4),C(﹣6,2),OD=2,
∴由勾股定理得:CD==,AD==,AC==,
∴CD2+AD2=AC2,
∴∠ADC=90°,
∴圆弧的长度是=π.
18.解:圆弧长是:=100π(米).
故答案是:100π.
19.解:(1)过点B作BF⊥CD,垂足为F,
∵AD∥BC,
∴∠ADB=∠CBD,
∵CB=CD,
∴∠CBD=∠CDB,
∴∠ADB=∠CDB.
在△ABD和△FBD中,
,
∴△ABD≌△FBD(AAS),
∴BF=BA,则点F在圆B上,
∴CD与⊙B相切;
(2)∵∠BCD=60°,CB=CD,
∴△BCD是等边三角形,
∴∠CBD=60°
∵BF⊥CD,
∴∠ABD=∠DBF=∠CBF=30°,
∴∠ABF=60°,
∵AB=BF=,
∴AD=DF=AB·tan30°=2,
∴阴影部分的面积=S△ABD﹣S扇形ABE
=
=.
20.解:(1)连接CD,如图,
∵∠ACB=90°,∠B=28°,
∴∠BAC=90°﹣28°=62°,
∵CA=CD,
∴∠CDA=∠CAD=62°,
∴∠ACD=180°﹣62°﹣62°=56°,
∴的度数为56°;
(2)∵D是AB的中点,∠ACB=90°,
∴CD=AD=BD=AB=1,
∵CD=CA,
∴△ACD为等边三角形,
∴∠ACD=60°,
∴阴影部分的面积=S扇形ACD﹣S△ACD
=﹣×12
=π﹣;
(3)过点C作CH⊥AD于H,
∴AH=DH=AD,
∵∠ACB=90°,CH⊥AB,
∴∠ACB=∠AHC,
∵∠A=∠A,
∴△ACH∽△△ABC,
∴AC:AB=AH:AC,
∴AC2=AH?AB,
即()2=AD?AB,
∴AD?AB=6.
21.(1)证明:连接AP,
∵AB是半圆O的直径,
∴∠APB=90°,
∴AP⊥BC.
∵PC=PB,
∴△ABC是等腰三角形,即AB=AC;
(2)解:①∵∠APB=90°,AB=4,∠ABC=30°,
∴AP=AB=2,
∴BP===2;
②连接OP,
∵∠ABC=30°,
∴∠PAB=60°,
∴∠POB=120°.
∵点O是AB的中点,
∴S△POB=S△PAB=×AP?PB=×2×2=,
∴S阴影=S扇形BOP﹣S△POB
=﹣
=π﹣.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
