1.1.2探索勾股定理 课件(共23张PPT))
文档属性
| 名称 | 1.1.2探索勾股定理 课件(共23张PPT)) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-21 17:45:51 | ||
图片预览




文档简介
(共23张PPT)
1.1.2探索勾股定理
第一章
勾股定理
2021-2022学年八年级数学上册同步(北师版)
1.掌握勾股定理及其验证.
2.能应用勾股定理解决一些实际问题。
学习目标
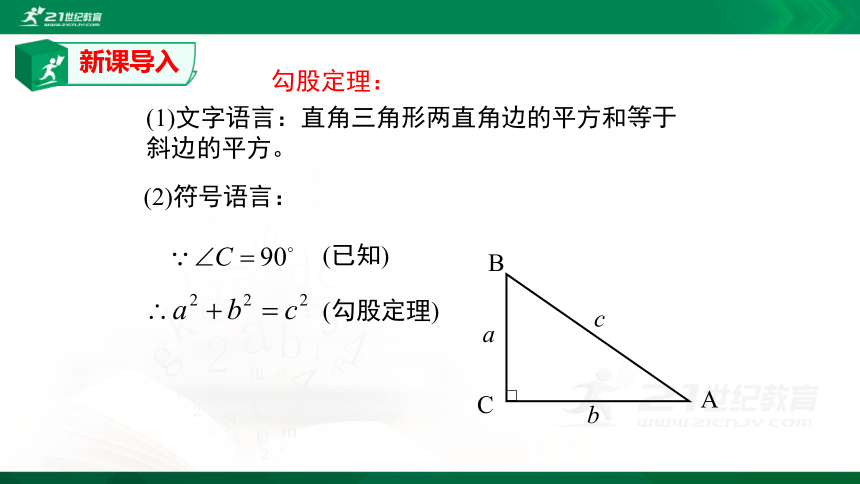
勾股定理:
(1)文字语言:直角三角形两直角边的平方和等于斜边的平方。
A
B
C
a
b
c
(2)符号语言:
(已知)
(勾股定理)
新课导入
勾股定理的验证
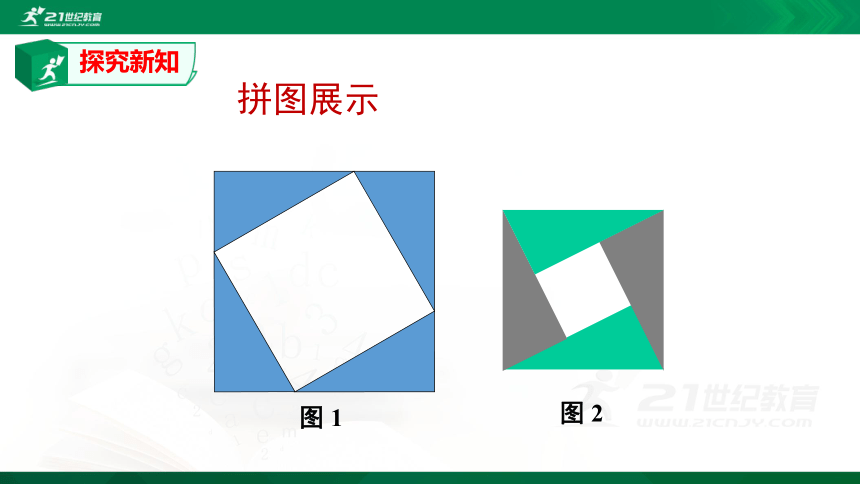
活动:请你利用自己准备的四个全等的直角三角形拼出以斜边为边长的正方形.
有不同的拼法吗?
探究新知
拼图展示
图
1
图
2
探究新知
据不完全统计,验证的方法有400多种,你有自己的方法吗?
问题:上节课我们认识了勾股定理,你还记得它的内容吗?那么如何验证勾股定理呢
?
探究新知
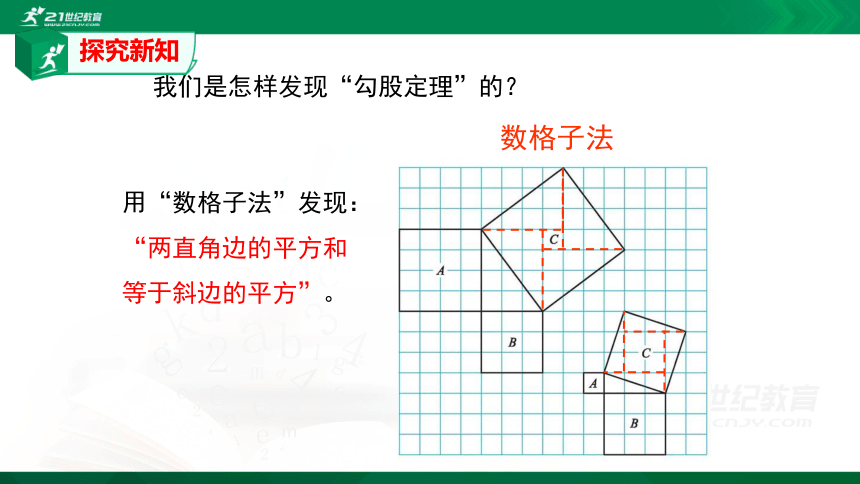
我们是怎样发现“勾股定理”的?
用“数格子法”发现:
“两直角边的平方和等于斜边的平方”。
数格子法
探究新知
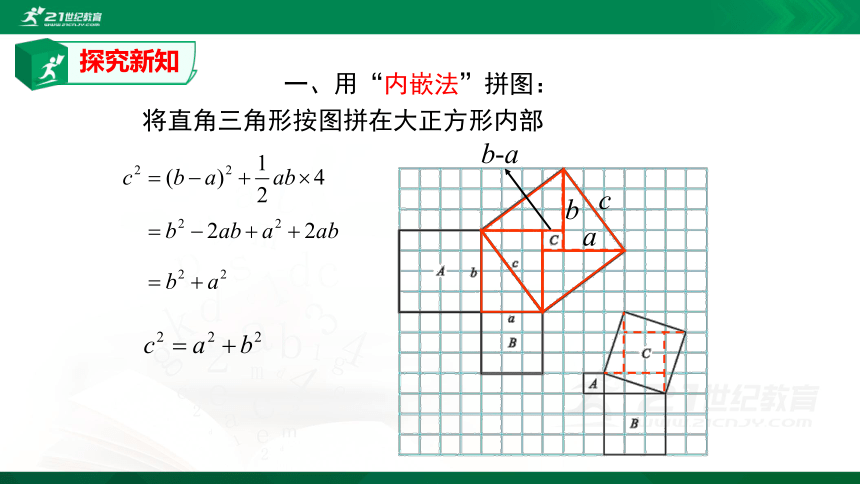
一、用“内嵌法”拼图:
将直角三角形按图拼在大正方形内部
b-a
a
b
c
探究新知
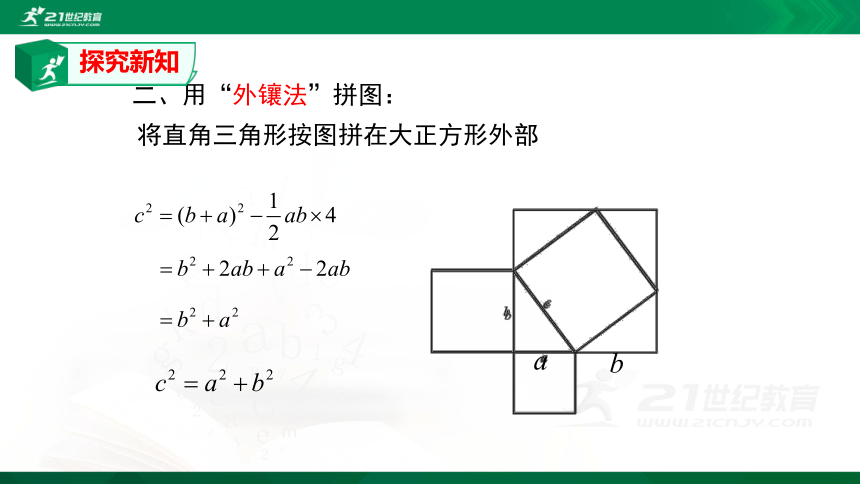
二、用“外镶法”拼图:
将直角三角形按图拼在大正方形外部
a
b
探究新知
如图是美国总统伽菲尔德(Garfield)于1876年给出的一种验证勾股定理的办法,你能利用它验证勾股定理吗?说一说这个方法和本节的探索方法的联系。
三、“总统证明法”
如图,梯形由三个直角三角形组合而成,利用面积公式,列出代数关系式,得
化简,得
探究新知
(2)拼梯形图:
运用梯形面积表达式进行证明。
新知归纳
“勾股定理”的验证方法:
(1)拼正方形图:
运用正方形面积表达式进行证明;
1、数形结合法:
勾股定理的简单应用
400米
500米
500
400
C
A
B
A
C
B
我方侦查员小王在就东西向公路400m处侦查,发现一辆敌方汽车在公路上疾驶,他赶紧拿出红外测距仪,测得汽车与他相距400m,10s后,汽车与他相距500m,你能帮小王计算敌方汽车的速度吗?
探究新知
解:由勾股定理,得AB2=BC2+AC2,
即
5002=BC2+4002,
所以,BC=300.
敌方汽车10s行驶了300m,那么它1h行驶的距离为300×6×60=108000(m)
即它行驶的速度为108km/h.
探究新知
2.如图,一根旗杆在离地面9
m处折断,旗杆顶部落在离旗杆底部12
m处.旗杆原来有多高?
12
m
9
m
解:设旗杆顶部到折断处的距离为x
m,根据勾股定理得
解得x=15,
15+9=24(m).
答:旗杆原来高24
m.
探究新知
1.湖的两端有A、B两点,从与BA方向成直角的BC方向上的点C测得CA=130米,CB=120米,则AB为(
)
A
B
C
A.50米
B.120米
C.100米
D.130米
130
120
?
A
课堂练习
2.如图,王大爷准备建一个蔬菜大棚,棚宽8m,高6m,长20m,棚的斜面用塑料薄膜遮盖,不计墙的厚度,阳光透过的最大面积是_________.
200m2
A
B
C
3.如图,太阳能热水器的支架AB长为90
cm,与AB垂直的BC长为120
cm.太阳能真空管AC有多长?
解:在Rt△ABC中,由勾股定理,
得
AC2=AB2+BC2,
AC2=902+1202,
AC=150(cm).
答:太阳能真空管AC长150
cm.
4.如图,在一条公路上有A、B两站相距25km,C、D为两个小镇,已知DA⊥AB,CB
⊥AB,
DA=15km,CB=
10km,现在要在公路边上建设一个加油站E,使得它到两镇的距离相等,请问E站应建在距A站多远处?
D
A
E
B
C
15
10
25-x
5.如图,折叠长方形ABCD的一边AD,使点D落在BC边的F点处,若AB=8cm,BC=10cm,求EC的长.
D
A
B
C
E
F
解:在Rt△ABF中,由勾股定理,
得
BF2=AF2-AB2=102-82
BF=6(cm).
∴CF=BC-BF=4.
设EC=x
,则EF=DE=8-x
,
在Rt△ECF中,根据勾股定理,
得
x2+
42=(8-x)2
解得
x=3.
所以EC的长为3
cm.
4.如图,某住宅小区在施工过程中留下了一块空地(图中的四边形ABCD),经测量,在四边形ABCD中,AB=3m,BC=4m,AD=13m,∠B=∠ACD=90°.小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问铺满这块空地共需花费多少元?
解:在Rt△ABC中,由勾股定理,
得
AC2=AB2+BC2,∴AC=5m,
在Rt△ACD中,由勾股定理,
得
CD2=AD2-AC2,∴CD=12m,
S草坪=SRt△ABC+SRt△ACD=
AB?BC+
AC?DC
=
(3×4+5×12)=36
m2.
故需要的费用为36×100=3600元.
知识:勾股定理
如果直角三角形两直角边长分别为a,b,斜边长为
c
,那么
.
方法:观察—猜想—探究—验证—归纳—应用;
思想:1.
特殊—一般
2.
数形结合思想
3.
方程的思想
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
1.1.2探索勾股定理
第一章
勾股定理
2021-2022学年八年级数学上册同步(北师版)
1.掌握勾股定理及其验证.
2.能应用勾股定理解决一些实际问题。
学习目标
勾股定理:
(1)文字语言:直角三角形两直角边的平方和等于斜边的平方。
A
B
C
a
b
c
(2)符号语言:
(已知)
(勾股定理)
新课导入
勾股定理的验证
活动:请你利用自己准备的四个全等的直角三角形拼出以斜边为边长的正方形.
有不同的拼法吗?
探究新知
拼图展示
图
1
图
2
探究新知
据不完全统计,验证的方法有400多种,你有自己的方法吗?
问题:上节课我们认识了勾股定理,你还记得它的内容吗?那么如何验证勾股定理呢
?
探究新知
我们是怎样发现“勾股定理”的?
用“数格子法”发现:
“两直角边的平方和等于斜边的平方”。
数格子法
探究新知
一、用“内嵌法”拼图:
将直角三角形按图拼在大正方形内部
b-a
a
b
c
探究新知
二、用“外镶法”拼图:
将直角三角形按图拼在大正方形外部
a
b
探究新知
如图是美国总统伽菲尔德(Garfield)于1876年给出的一种验证勾股定理的办法,你能利用它验证勾股定理吗?说一说这个方法和本节的探索方法的联系。
三、“总统证明法”
如图,梯形由三个直角三角形组合而成,利用面积公式,列出代数关系式,得
化简,得
探究新知
(2)拼梯形图:
运用梯形面积表达式进行证明。
新知归纳
“勾股定理”的验证方法:
(1)拼正方形图:
运用正方形面积表达式进行证明;
1、数形结合法:
勾股定理的简单应用
400米
500米
500
400
C
A
B
A
C
B
我方侦查员小王在就东西向公路400m处侦查,发现一辆敌方汽车在公路上疾驶,他赶紧拿出红外测距仪,测得汽车与他相距400m,10s后,汽车与他相距500m,你能帮小王计算敌方汽车的速度吗?
探究新知
解:由勾股定理,得AB2=BC2+AC2,
即
5002=BC2+4002,
所以,BC=300.
敌方汽车10s行驶了300m,那么它1h行驶的距离为300×6×60=108000(m)
即它行驶的速度为108km/h.
探究新知
2.如图,一根旗杆在离地面9
m处折断,旗杆顶部落在离旗杆底部12
m处.旗杆原来有多高?
12
m
9
m
解:设旗杆顶部到折断处的距离为x
m,根据勾股定理得
解得x=15,
15+9=24(m).
答:旗杆原来高24
m.
探究新知
1.湖的两端有A、B两点,从与BA方向成直角的BC方向上的点C测得CA=130米,CB=120米,则AB为(
)
A
B
C
A.50米
B.120米
C.100米
D.130米
130
120
?
A
课堂练习
2.如图,王大爷准备建一个蔬菜大棚,棚宽8m,高6m,长20m,棚的斜面用塑料薄膜遮盖,不计墙的厚度,阳光透过的最大面积是_________.
200m2
A
B
C
3.如图,太阳能热水器的支架AB长为90
cm,与AB垂直的BC长为120
cm.太阳能真空管AC有多长?
解:在Rt△ABC中,由勾股定理,
得
AC2=AB2+BC2,
AC2=902+1202,
AC=150(cm).
答:太阳能真空管AC长150
cm.
4.如图,在一条公路上有A、B两站相距25km,C、D为两个小镇,已知DA⊥AB,CB
⊥AB,
DA=15km,CB=
10km,现在要在公路边上建设一个加油站E,使得它到两镇的距离相等,请问E站应建在距A站多远处?
D
A
E
B
C
15
10
25-x
5.如图,折叠长方形ABCD的一边AD,使点D落在BC边的F点处,若AB=8cm,BC=10cm,求EC的长.
D
A
B
C
E
F
解:在Rt△ABF中,由勾股定理,
得
BF2=AF2-AB2=102-82
BF=6(cm).
∴CF=BC-BF=4.
设EC=x
,则EF=DE=8-x
,
在Rt△ECF中,根据勾股定理,
得
x2+
42=(8-x)2
解得
x=3.
所以EC的长为3
cm.
4.如图,某住宅小区在施工过程中留下了一块空地(图中的四边形ABCD),经测量,在四边形ABCD中,AB=3m,BC=4m,AD=13m,∠B=∠ACD=90°.小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问铺满这块空地共需花费多少元?
解:在Rt△ABC中,由勾股定理,
得
AC2=AB2+BC2,∴AC=5m,
在Rt△ACD中,由勾股定理,
得
CD2=AD2-AC2,∴CD=12m,
S草坪=SRt△ABC+SRt△ACD=
AB?BC+
AC?DC
=
(3×4+5×12)=36
m2.
故需要的费用为36×100=3600元.
知识:勾股定理
如果直角三角形两直角边长分别为a,b,斜边长为
c
,那么
.
方法:观察—猜想—探究—验证—归纳—应用;
思想:1.
特殊—一般
2.
数形结合思想
3.
方程的思想
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
