1.1.1探索勾股定理 课件(共31张PPT)
文档属性
| 名称 | 1.1.1探索勾股定理 课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-21 17:49:16 | ||
图片预览




文档简介
(共31张PPT)
1.1.1探索勾股定理
第一章
勾股定理
2021-2022学年八年级数学上册同步(北师版)
1、用数格子的办法体验勾股定理的探索过程。
2、理解勾股定理,会初步运用勾股定理进行简单的计算和实际运用。
学习目标
如图,这是一幅美丽的图案,仔细观察,你能发现这幅图中的奥秘吗?带着疑问我们来一起探索吧.
新课导入
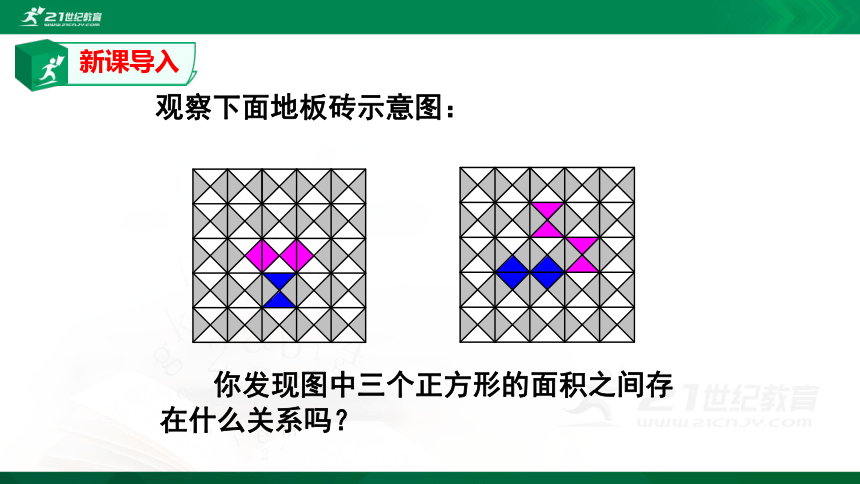
观察下面地板砖示意图:
你发现图中三个正方形的面积之间存在什么关系吗?
新课导入
勾股定理的初步认识
1.阅读课本P2
回答问题
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图1-1
图1-2
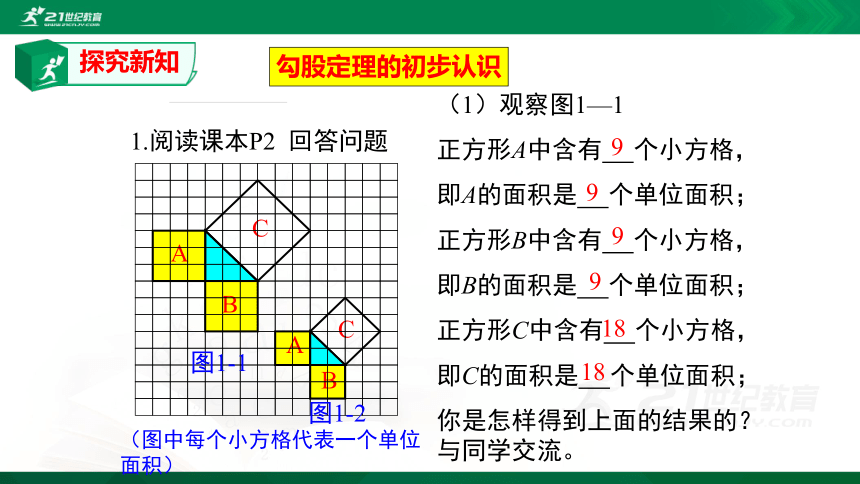
(1)观察图1—1
正方形A中含有
个小方格,
即A的面积是
个单位面积;
正方形B中含有
个小方格,
即B的面积是
个单位面积;
正方形C中含有
个小方格,
即C的面积是
个单位面积;
你是怎样得到上面的结果的?与同学交流。
9
9
9
9
18
18
探究新知
1.阅读课本P2
回答问题
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图1-1
图1-2
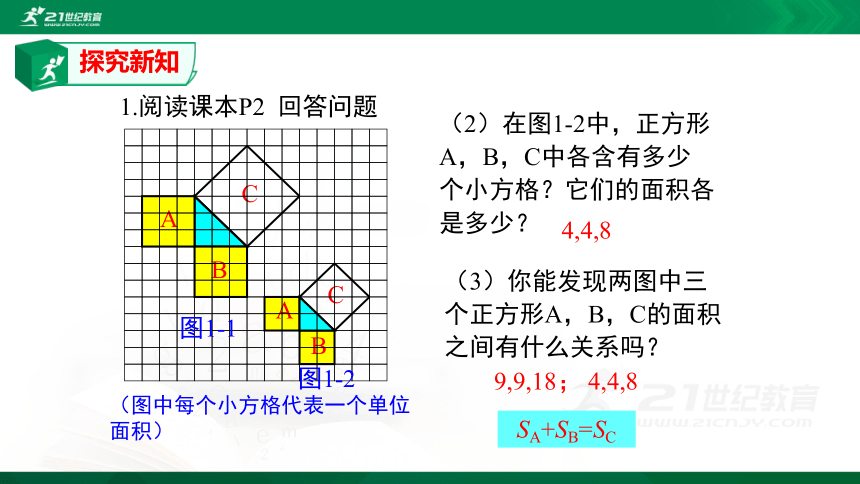
(2)在图1-2中,正方形A,B,C中各含有多少个小方格?它们的面积各是多少?
(3)你能发现两图中三个正方形A,B,C的面积之间有什么关系吗?
SA+SB=SC
4,4,8
9,9,18;
4,4,8
探究新知
A
B
C
A
B
C
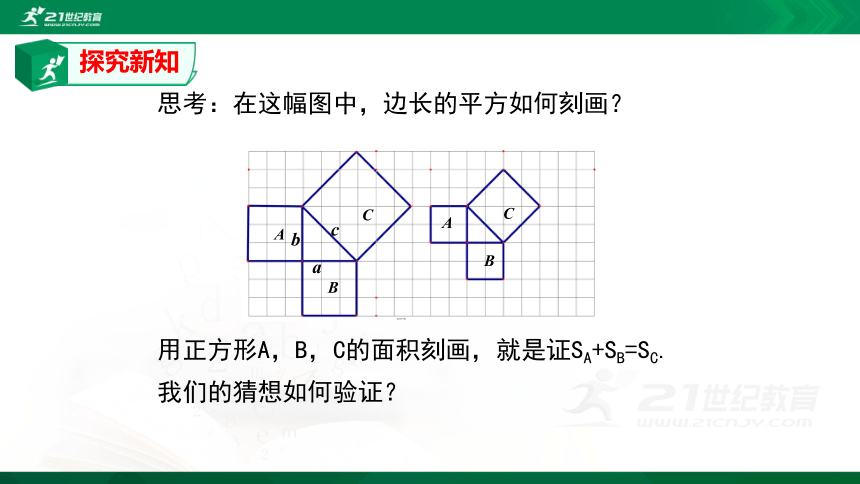
思考:在这幅图中,边长的平方如何刻画?
用正方形A,B,C的面积刻画,就是证SA+SB=SC.
我们的猜想如何验证?
c
b
a
探究新知
A
B
C
A
B
C
请想办法计算左边图形中A,B,C的面积.
你用什么办法计算C的面积呢?
SA=9
SB=9
SC=18
数格子
探究新知
验证法1
方法:可把正方形
C分成两个全等的
等腰直角三角形,
可求得正方形C的
面积为18.
割
C
B
A
还可以用什么办法计算C的面积呢?
探究新知
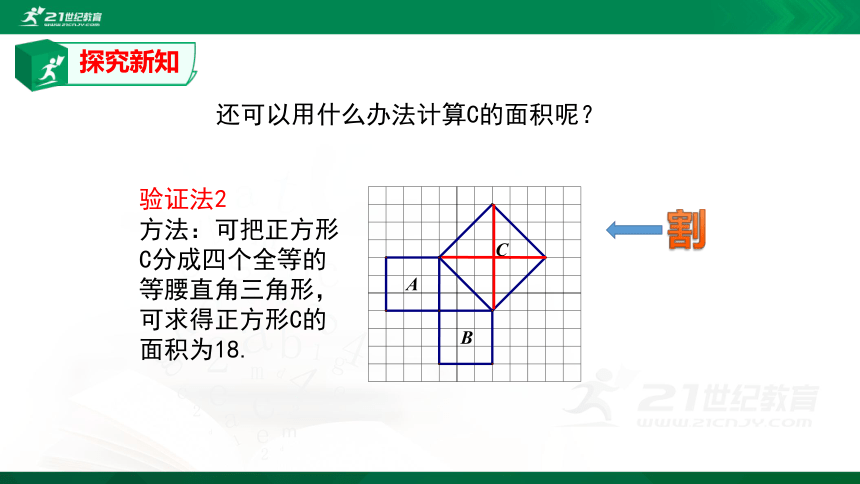
验证法2
方法:可把正方形
C分成四个全等的
等腰直角三角形,
可求得正方形C的
面积为18.
割
C
B
A
还可以用什么办法计算C的面积呢?
探究新知
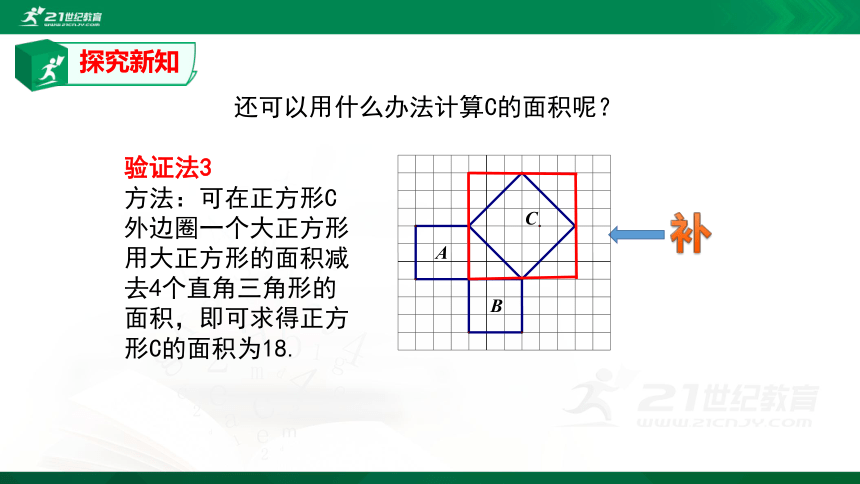
验证法3
方法:可在正方形C
外边圈一个大正方形
用大正方形的面积减
去4个直角三角形的
面积,即可求得正方
形C的面积为18.
补
C
B
A
还可以用什么办法计算C的面积呢?
探究新知
C
B
A
SA=9
SB=9
SC=18
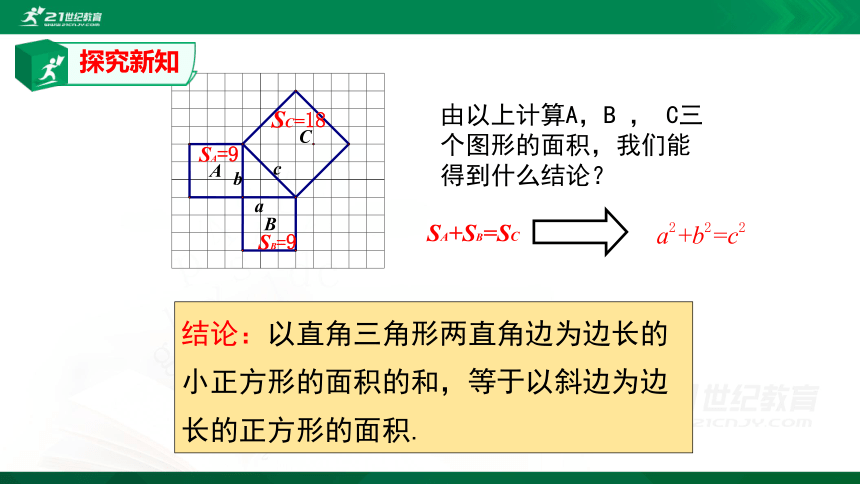
由以上计算A,B
,
C三
个图形的面积,我们能
得到什么结论?
SA+SB=SC
c
b
a
结论:以直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积.
探究新知
几何语言:
∵在Rt△ABC中
,∠C=90°,
∴a2+b2=c2(勾股定理).
a
A
B
C
b
c
∟
总结归纳
定理揭示了直角三角形三边之间的关系.
直角三角形两直角边的平方和等于斜边的平方.如果a,b和c分别表示直角三角形的两直角边和斜边,那么a2+b2=c2.
勾股定理
求下列直角三角形中未知边的长:
8
x
17
12
5
x
解:由勾股定理可得:
82+
x2=172
即:x2=172-82
x=15
解:由勾股定理可得:
52+
122=
x2
即:x2=52+122
x=13
针对练习
例1
已知∠ACB=90°,CD⊥AB,AC=3,BC=4.求CD的长.
利用勾股定理进行计算
解:由勾股定理可得,
AB2=AC2+BC2=25,
即
AB=5.
根据三角形面积公式,
∴
AC×BC=
AB×CD.
∴
CD=
.
A
D
B
C
3
4
探究新知
方法总结
由直角三角形的面积求法可知直角三角形两直角边的积等于斜边与斜边上高的积,这个规律也称“弦高公式”,它常与勾股定理联合使用.
例2
如图,已知AD是△ABC的中线.
求证:AB2+AC2=2(AD2+CD2).
证明:如图,过点A作AE⊥BC于点E.
在Rt△ACE、Rt△ABE和Rt△ADE中,
AB2=AE2+BE2,AC2=AE2+CE2,AE2=AD2-ED2,
∴AB2+AC2=(AE2+BE2)+(AE2+CE2)
=2AD2+DB2+DC2+2DE(DC-DB).
又∵AD是△ABC的中线,
∴BD=CD,
∴AB2+AC2=2AD2+2DC2=2(AD2+CD2).
E
例题讲解
方法总结
构造直角三角形,利用勾股定理把需要证明的线段联系起来.一般地,涉及线段之间的平方关系问题时,通常沿着这个思路去分析问题.
解:当高AD在△ABC内部时,如图①.
在Rt△ABD中,由勾股定理,
得BD2=AB2-AD2=202-122=162,
∴BD=16;
在Rt△ACD中,由勾股定理,
得CD2=AC2-AD2=152-122=81,
∴CD=9.
∴BC=BD+CD=25,
∴△ABC的周长为25+20+15=60.
例3
在△ABC中,AB=20,AC=15,AD为BC边上的高,且AD=12,求△ABC的周长.
例题讲解
题中未给出图形,作高构造直角三角形时,易漏掉钝角三角形的情况.如在本例题中,易只考虑高AD在△ABC内的情形,忽视高AD在△ABC外的情形.
当高AD在△ABC外部时,如图②.
同理可得
BD=16,CD=9.
∴BC=BD-CD=7,
∴△ABC的周长为7+20+15=42.
综上所述,△ABC的周长为42或60.
方法总结
例题讲解
解析:因为AE=BE,
所以S△ABE=
AE·BE=
AE2.
又因为AE2+BE2=AB2,
所以2AE2=AB2,
所以S△ABE=
AB2=
;
同理可得S△AHC+S△BCF=
AC2+
BC2.
又因为AC2+BC2=AB2,
所以阴影部分的面积为
AB2=
.
例4
如图,以Rt△ABC的三边长为斜边分别向外作等腰直角三角形.若斜边AB=3,则图中△ABE的面积为________,阴影部分的面积为________.
例题讲解
求解与直角三角形三边有关的图形面积时,要结合图形想办法把图形的面积与直角三角形三边的平方联系起来,再利用勾股定理找到图形面积之间的等量关系.
方法总结
一、判断题.
1.△ABC的两边AB=5,AC=12,则BC=13
(
)
2.△ABC的a=6,b=8,则c=10
(
)
二、填空题
3.在△ABC中,
∠C=90°,AC=6,CB=8,则
△ABC面积为_____,斜边为上的高为______.
?
?
24
4.8
A
B
C
D
课堂练习
4.在△ABC中,∠C=90?,
(1)???
若a=5,b=12,则c=________;
(2)???
若a=15,c=25,则b=________;
(3)???
若c=61,b=60,则a=________;
(4)???
若a:b=3:4,c=10,则a=________,b=________;
(5)???
若a:c=3:5
,b=8,则a=________;
20
13
11
6
8
6
5.求出下列字母所代表的正方形的面积.
正方形A面积为625
正方形B面积为144
B
A
6
.求出下列三角形中未知边的长度.
(1)
(2)
解:(1)由勾股定理得:
x2=62+82=100.
x
8
6
y
13
5
因为x>0,所以x=10.
(2)由勾股定理得:
y2=132-52=144.
因为y>0,所以y=12.
7.强大的台风使得一个旗杆在离地面9
m处折断倒下,旗杆顶部落在离旗杆底部12
m处,请问旗杆折断前有多高?
解:设旗杆折断前有x
m,由勾股定理得:
(x-9)2=122+92
因为x-9>0,所以x-9=15,所以x=24.
8.台风使得一个旗杆折断倒下,倒下部分长比未倒下部分长4
m,如图,旗杆顶部落在离旗杆底部12
m处,旗杆折断之前有多高?
即:8x=128.解得x=16.
∴x+4=20(m),16+20=36(m).
答:旗杆折断之前有36
m高.
解:设未折断部分为x
m,则折断部分为(x+4)m.根据题意得
知识:
如果·直角三角形两直角边长分别为a,b,斜边长为
c
,那么
方法:
1.
观察—探索—猜想—验证—归纳—应用;
2.
“割、补、拼、接”法.
思想:
1.
特殊—一般—特殊;
2.
数形结合思想.
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
1.1.1探索勾股定理
第一章
勾股定理
2021-2022学年八年级数学上册同步(北师版)
1、用数格子的办法体验勾股定理的探索过程。
2、理解勾股定理,会初步运用勾股定理进行简单的计算和实际运用。
学习目标
如图,这是一幅美丽的图案,仔细观察,你能发现这幅图中的奥秘吗?带着疑问我们来一起探索吧.
新课导入
观察下面地板砖示意图:
你发现图中三个正方形的面积之间存在什么关系吗?
新课导入
勾股定理的初步认识
1.阅读课本P2
回答问题
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图1-1
图1-2
(1)观察图1—1
正方形A中含有
个小方格,
即A的面积是
个单位面积;
正方形B中含有
个小方格,
即B的面积是
个单位面积;
正方形C中含有
个小方格,
即C的面积是
个单位面积;
你是怎样得到上面的结果的?与同学交流。
9
9
9
9
18
18
探究新知
1.阅读课本P2
回答问题
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图1-1
图1-2
(2)在图1-2中,正方形A,B,C中各含有多少个小方格?它们的面积各是多少?
(3)你能发现两图中三个正方形A,B,C的面积之间有什么关系吗?
SA+SB=SC
4,4,8
9,9,18;
4,4,8
探究新知
A
B
C
A
B
C
思考:在这幅图中,边长的平方如何刻画?
用正方形A,B,C的面积刻画,就是证SA+SB=SC.
我们的猜想如何验证?
c
b
a
探究新知
A
B
C
A
B
C
请想办法计算左边图形中A,B,C的面积.
你用什么办法计算C的面积呢?
SA=9
SB=9
SC=18
数格子
探究新知
验证法1
方法:可把正方形
C分成两个全等的
等腰直角三角形,
可求得正方形C的
面积为18.
割
C
B
A
还可以用什么办法计算C的面积呢?
探究新知
验证法2
方法:可把正方形
C分成四个全等的
等腰直角三角形,
可求得正方形C的
面积为18.
割
C
B
A
还可以用什么办法计算C的面积呢?
探究新知
验证法3
方法:可在正方形C
外边圈一个大正方形
用大正方形的面积减
去4个直角三角形的
面积,即可求得正方
形C的面积为18.
补
C
B
A
还可以用什么办法计算C的面积呢?
探究新知
C
B
A
SA=9
SB=9
SC=18
由以上计算A,B
,
C三
个图形的面积,我们能
得到什么结论?
SA+SB=SC
c
b
a
结论:以直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积.
探究新知
几何语言:
∵在Rt△ABC中
,∠C=90°,
∴a2+b2=c2(勾股定理).
a
A
B
C
b
c
∟
总结归纳
定理揭示了直角三角形三边之间的关系.
直角三角形两直角边的平方和等于斜边的平方.如果a,b和c分别表示直角三角形的两直角边和斜边,那么a2+b2=c2.
勾股定理
求下列直角三角形中未知边的长:
8
x
17
12
5
x
解:由勾股定理可得:
82+
x2=172
即:x2=172-82
x=15
解:由勾股定理可得:
52+
122=
x2
即:x2=52+122
x=13
针对练习
例1
已知∠ACB=90°,CD⊥AB,AC=3,BC=4.求CD的长.
利用勾股定理进行计算
解:由勾股定理可得,
AB2=AC2+BC2=25,
即
AB=5.
根据三角形面积公式,
∴
AC×BC=
AB×CD.
∴
CD=
.
A
D
B
C
3
4
探究新知
方法总结
由直角三角形的面积求法可知直角三角形两直角边的积等于斜边与斜边上高的积,这个规律也称“弦高公式”,它常与勾股定理联合使用.
例2
如图,已知AD是△ABC的中线.
求证:AB2+AC2=2(AD2+CD2).
证明:如图,过点A作AE⊥BC于点E.
在Rt△ACE、Rt△ABE和Rt△ADE中,
AB2=AE2+BE2,AC2=AE2+CE2,AE2=AD2-ED2,
∴AB2+AC2=(AE2+BE2)+(AE2+CE2)
=2AD2+DB2+DC2+2DE(DC-DB).
又∵AD是△ABC的中线,
∴BD=CD,
∴AB2+AC2=2AD2+2DC2=2(AD2+CD2).
E
例题讲解
方法总结
构造直角三角形,利用勾股定理把需要证明的线段联系起来.一般地,涉及线段之间的平方关系问题时,通常沿着这个思路去分析问题.
解:当高AD在△ABC内部时,如图①.
在Rt△ABD中,由勾股定理,
得BD2=AB2-AD2=202-122=162,
∴BD=16;
在Rt△ACD中,由勾股定理,
得CD2=AC2-AD2=152-122=81,
∴CD=9.
∴BC=BD+CD=25,
∴△ABC的周长为25+20+15=60.
例3
在△ABC中,AB=20,AC=15,AD为BC边上的高,且AD=12,求△ABC的周长.
例题讲解
题中未给出图形,作高构造直角三角形时,易漏掉钝角三角形的情况.如在本例题中,易只考虑高AD在△ABC内的情形,忽视高AD在△ABC外的情形.
当高AD在△ABC外部时,如图②.
同理可得
BD=16,CD=9.
∴BC=BD-CD=7,
∴△ABC的周长为7+20+15=42.
综上所述,△ABC的周长为42或60.
方法总结
例题讲解
解析:因为AE=BE,
所以S△ABE=
AE·BE=
AE2.
又因为AE2+BE2=AB2,
所以2AE2=AB2,
所以S△ABE=
AB2=
;
同理可得S△AHC+S△BCF=
AC2+
BC2.
又因为AC2+BC2=AB2,
所以阴影部分的面积为
AB2=
.
例4
如图,以Rt△ABC的三边长为斜边分别向外作等腰直角三角形.若斜边AB=3,则图中△ABE的面积为________,阴影部分的面积为________.
例题讲解
求解与直角三角形三边有关的图形面积时,要结合图形想办法把图形的面积与直角三角形三边的平方联系起来,再利用勾股定理找到图形面积之间的等量关系.
方法总结
一、判断题.
1.△ABC的两边AB=5,AC=12,则BC=13
(
)
2.△ABC的a=6,b=8,则c=10
(
)
二、填空题
3.在△ABC中,
∠C=90°,AC=6,CB=8,则
△ABC面积为_____,斜边为上的高为______.
?
?
24
4.8
A
B
C
D
课堂练习
4.在△ABC中,∠C=90?,
(1)???
若a=5,b=12,则c=________;
(2)???
若a=15,c=25,则b=________;
(3)???
若c=61,b=60,则a=________;
(4)???
若a:b=3:4,c=10,则a=________,b=________;
(5)???
若a:c=3:5
,b=8,则a=________;
20
13
11
6
8
6
5.求出下列字母所代表的正方形的面积.
正方形A面积为625
正方形B面积为144
B
A
6
.求出下列三角形中未知边的长度.
(1)
(2)
解:(1)由勾股定理得:
x2=62+82=100.
x
8
6
y
13
5
因为x>0,所以x=10.
(2)由勾股定理得:
y2=132-52=144.
因为y>0,所以y=12.
7.强大的台风使得一个旗杆在离地面9
m处折断倒下,旗杆顶部落在离旗杆底部12
m处,请问旗杆折断前有多高?
解:设旗杆折断前有x
m,由勾股定理得:
(x-9)2=122+92
因为x-9>0,所以x-9=15,所以x=24.
8.台风使得一个旗杆折断倒下,倒下部分长比未倒下部分长4
m,如图,旗杆顶部落在离旗杆底部12
m处,旗杆折断之前有多高?
即:8x=128.解得x=16.
∴x+4=20(m),16+20=36(m).
答:旗杆折断之前有36
m高.
解:设未折断部分为x
m,则折断部分为(x+4)m.根据题意得
知识:
如果·直角三角形两直角边长分别为a,b,斜边长为
c
,那么
方法:
1.
观察—探索—猜想—验证—归纳—应用;
2.
“割、补、拼、接”法.
思想:
1.
特殊—一般—特殊;
2.
数形结合思想.
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
