3.3 二次函数y=ax?的图象与性质 课件(共23张PPT)
文档属性
| 名称 | 3.3 二次函数y=ax?的图象与性质 课件(共23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-22 19:27:36 | ||
图片预览







文档简介
(共23张PPT)
第三章
二次函数
知识点一
二次函数y=±x2的图象与性质
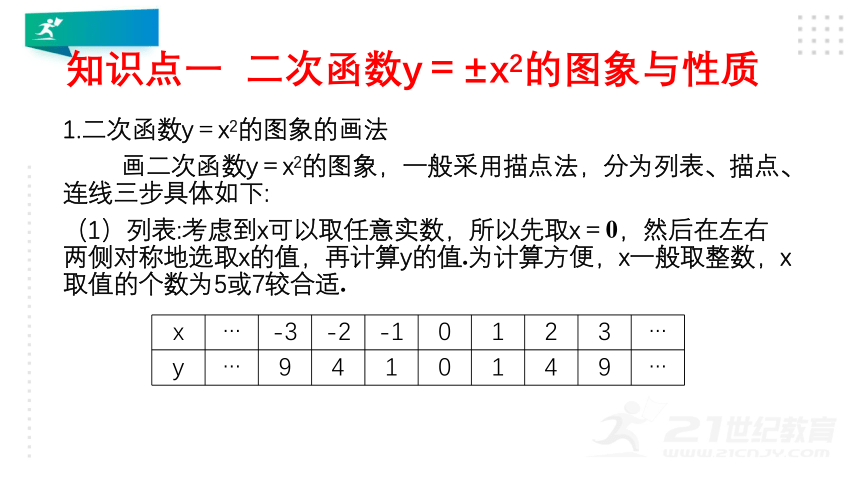
1.二次函数y=x2的图象的画法
画二次函数y=x2的图象,一般采用描点法,分为列表、描点、连线三步具体如下:
(1)列表:考虑到x可以取任意实数,所以先取x=0,然后在左右两侧对称地选取x的值,再计算y的值.为计算方便,x一般取整数,x取值的个数为5或7较合适.
x
…
-3
-2
-1
0
1
2
3
…
y
…
9
4
1
0
1
4
9
…
(2)描点:如图①所示.
(3)连线:如图②所示,用平滑曲线顺次(自变量的取值由小到大或由大到小)连接各点,连线时注意平滑,两边要顺势伸展出去一部分.由于画出的图象是近似的,因此点选取得越多图象越精确.
2.二次函数y=-x2的图象的画法
二次函数y=-x2的图象的画法与二次函数y=x2的图象的画法类似,只是图象的开口向下.
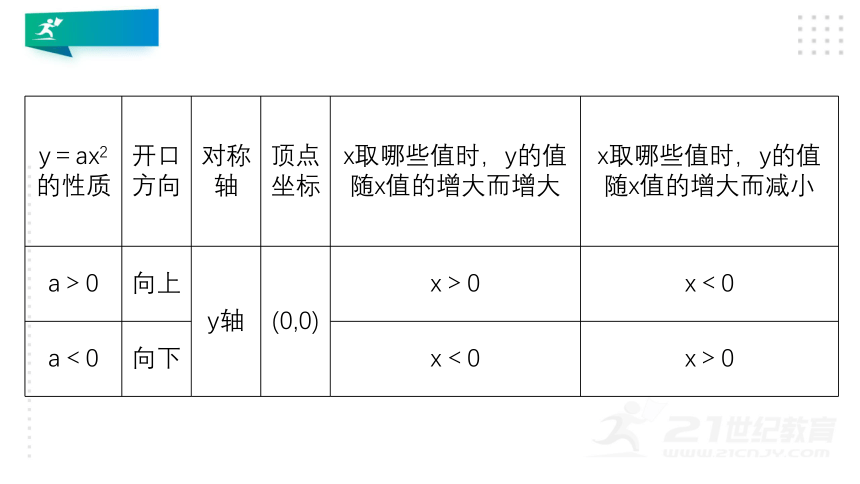
3.二次函数y=±x2的图象与性质
?
y=x2
y=-x2
图象
示意图
?
?
开口方向
向上,顶点是最低点
向下,顶点是最高点
对称轴
y轴
y轴
顶点坐标
(0,0)
(0,0)
性质
增减性
当x<0时,y随x的增大而减小,当x>0时,y随x的增大而增大
当x<0时,y随x的增大而增大,当x>0时,y随x的增大而减小
最值
当x=0时,y最小值=0
当x=0时,y最大值=0
知识点二
二次函数y=ax2(a≠0)的图象与性质
一般地,二次函数y=ax2(a≠0)的图象是抛物线.我们把二次函数y=ax2(a≠0)的图象叫做抛物线y=ax2(a≠0).
抛物线y=ax2(a≠0)的对称轴是y轴,它的顶点是坐标原点.当a>0时,抛物线的开口向上,顶点是它的最低点;当a<0时,抛物线的开口向下,顶点是它的最高点.
具体如下表所示:
y=ax2的性质
开口方向
对称轴
顶点
坐标
x取哪些值时,y的值随x值的增大而增大
x取哪些值时,y的值随x值的增大而减小
a>0
向上
y轴
(0,0)
x>0
x<0
a<0
向下
x<0
x>0
温馨提示
对于抛物线y=ax2(a≠0)要注意从对称轴、顶点坐标、开口方向三个方面把握.
温馨提示
对于抛物线y=ax2(a≠0)要注意从对称轴、顶点坐标、开口方向三个方面把握.
规律总结
抛物线y=ax2(a≠0)的开口大小由|a|决定,|a|越大,抛物线的开口越小;|a|越小,抛物线的开口越大.要注意是|a|的大小,而不是a本身的大小.
例2
已知四个二次函数的图象如图所示,那么a1,a2,a3,a4的大小关系是___________________.(请用“>”连接排序)
解析
抛物线y=a1x2与y=a2x2的开口向上,其中前者开口小,所以a1>a2>0.
抛物线y=a3x2与y=a4x2的开口向下,其中后者开口小,所以a4<a3<0,
所以a1>a2>a3>a4
.
经典例题
题型一
利用抛物线y=ax2(a≠0)比较函数值的大小
例1
已知a<-1,若点A(a-1,y1)、B(a,y2)、C(a+1,y3)都在函数y=-2x2的图象上,则(
)
A.y3<y2<y1
B.y1<y3<y2
C.y1<y2<y3
D.y2<y1<y3
题型一
利用抛物线y=ax2(a≠0)比较函数值的大小
例1
已知a<-1,若点A(a-1,y1)、B(a,y2)、C(a+1,y3)都在函数y=-2x2的图象上,则(
)
A.y3<y2<y1
B.y1<y3<y2
C.y1<y2<y3
D.y2<y1<y3
解析
∵a<-1,∴a-1<a<a+1<0.
∵函数y=-2x2的图象开口向下,顶点坐标为(0,0),当x<0时,y随x的增大而增大,∴y1<y2<y3
.
题型一
利用抛物线y=ax2(a≠0)比较函数值的大小
例1
已知a<-1,若点A(a-1,y1)、B(a,y2)、C(a+1,y3)都在函数y=-2x2的图象上,则(
C
)
A.y3<y2<y1
B.y1<y3<y2
C.y1<y2<y3
D.y2<y1<y3
解析
∵a<-1,∴a-1<a<a+1<0.
∵函数y=-2x2的图象开口向下,顶点坐标为(0,0),当x<0时,y随x的增大而增大,∴y1<y2<y3
.
方法归纳
利用抛物线比较函数值的大小,先根据顶点坐标、对称轴、开口方向画出草图,明确顶点左右两侧抛物线的增减性,然后根据各点的横坐标在抛物线上大致描出各点,根据各点的位置判断纵坐标,即函数值的大小此法以形定数,避免了死记硬背二次函数的性质所导致的错误.
题型二
二次函数y=ax2(a≠0)与其他函数的图象综合题
例2
二次函数y=ax2与一次函数y=ax+a在同一坐标系中的大致图象可能是(
)
解析
由一次函数y=ax+a可知,一次函数的图象与x轴交于点(-1,0),排除A,B项.
当a>0时,二次函数的图象开口向上,一次函数的图象经过第一、二、三象限,D项符合.
当a<0时,二次函数的图象开口向下,一次函数的图象经过第二、三、四象限,排除C项.
故答案选D.
解析
由一次函数y=ax+a可知,一次函数的图象与x轴交于点(-1,0),排除A,B项.
当a>0时,二次函数的图象开口向上,一次函数的图象经过第一、二、三象限,D项符合.
当a<0时,二次函数的图象开口向下,一次函数的图象经过第二、三、四象限,排除C项.
故答案选D.
点拨
解此类题除了逐项判断外,较简捷的方法是按照字母系数的正负分情况讨论,直接选出符合某种情况的图象.
第三章
二次函数
知识点一
二次函数y=±x2的图象与性质
1.二次函数y=x2的图象的画法
画二次函数y=x2的图象,一般采用描点法,分为列表、描点、连线三步具体如下:
(1)列表:考虑到x可以取任意实数,所以先取x=0,然后在左右两侧对称地选取x的值,再计算y的值.为计算方便,x一般取整数,x取值的个数为5或7较合适.
x
…
-3
-2
-1
0
1
2
3
…
y
…
9
4
1
0
1
4
9
…
(2)描点:如图①所示.
(3)连线:如图②所示,用平滑曲线顺次(自变量的取值由小到大或由大到小)连接各点,连线时注意平滑,两边要顺势伸展出去一部分.由于画出的图象是近似的,因此点选取得越多图象越精确.
2.二次函数y=-x2的图象的画法
二次函数y=-x2的图象的画法与二次函数y=x2的图象的画法类似,只是图象的开口向下.
3.二次函数y=±x2的图象与性质
?
y=x2
y=-x2
图象
示意图
?
?
开口方向
向上,顶点是最低点
向下,顶点是最高点
对称轴
y轴
y轴
顶点坐标
(0,0)
(0,0)
性质
增减性
当x<0时,y随x的增大而减小,当x>0时,y随x的增大而增大
当x<0时,y随x的增大而增大,当x>0时,y随x的增大而减小
最值
当x=0时,y最小值=0
当x=0时,y最大值=0
知识点二
二次函数y=ax2(a≠0)的图象与性质
一般地,二次函数y=ax2(a≠0)的图象是抛物线.我们把二次函数y=ax2(a≠0)的图象叫做抛物线y=ax2(a≠0).
抛物线y=ax2(a≠0)的对称轴是y轴,它的顶点是坐标原点.当a>0时,抛物线的开口向上,顶点是它的最低点;当a<0时,抛物线的开口向下,顶点是它的最高点.
具体如下表所示:
y=ax2的性质
开口方向
对称轴
顶点
坐标
x取哪些值时,y的值随x值的增大而增大
x取哪些值时,y的值随x值的增大而减小
a>0
向上
y轴
(0,0)
x>0
x<0
a<0
向下
x<0
x>0
温馨提示
对于抛物线y=ax2(a≠0)要注意从对称轴、顶点坐标、开口方向三个方面把握.
温馨提示
对于抛物线y=ax2(a≠0)要注意从对称轴、顶点坐标、开口方向三个方面把握.
规律总结
抛物线y=ax2(a≠0)的开口大小由|a|决定,|a|越大,抛物线的开口越小;|a|越小,抛物线的开口越大.要注意是|a|的大小,而不是a本身的大小.
例2
已知四个二次函数的图象如图所示,那么a1,a2,a3,a4的大小关系是___________________.(请用“>”连接排序)
解析
抛物线y=a1x2与y=a2x2的开口向上,其中前者开口小,所以a1>a2>0.
抛物线y=a3x2与y=a4x2的开口向下,其中后者开口小,所以a4<a3<0,
所以a1>a2>a3>a4
.
经典例题
题型一
利用抛物线y=ax2(a≠0)比较函数值的大小
例1
已知a<-1,若点A(a-1,y1)、B(a,y2)、C(a+1,y3)都在函数y=-2x2的图象上,则(
)
A.y3<y2<y1
B.y1<y3<y2
C.y1<y2<y3
D.y2<y1<y3
题型一
利用抛物线y=ax2(a≠0)比较函数值的大小
例1
已知a<-1,若点A(a-1,y1)、B(a,y2)、C(a+1,y3)都在函数y=-2x2的图象上,则(
)
A.y3<y2<y1
B.y1<y3<y2
C.y1<y2<y3
D.y2<y1<y3
解析
∵a<-1,∴a-1<a<a+1<0.
∵函数y=-2x2的图象开口向下,顶点坐标为(0,0),当x<0时,y随x的增大而增大,∴y1<y2<y3
.
题型一
利用抛物线y=ax2(a≠0)比较函数值的大小
例1
已知a<-1,若点A(a-1,y1)、B(a,y2)、C(a+1,y3)都在函数y=-2x2的图象上,则(
C
)
A.y3<y2<y1
B.y1<y3<y2
C.y1<y2<y3
D.y2<y1<y3
解析
∵a<-1,∴a-1<a<a+1<0.
∵函数y=-2x2的图象开口向下,顶点坐标为(0,0),当x<0时,y随x的增大而增大,∴y1<y2<y3
.
方法归纳
利用抛物线比较函数值的大小,先根据顶点坐标、对称轴、开口方向画出草图,明确顶点左右两侧抛物线的增减性,然后根据各点的横坐标在抛物线上大致描出各点,根据各点的位置判断纵坐标,即函数值的大小此法以形定数,避免了死记硬背二次函数的性质所导致的错误.
题型二
二次函数y=ax2(a≠0)与其他函数的图象综合题
例2
二次函数y=ax2与一次函数y=ax+a在同一坐标系中的大致图象可能是(
)
解析
由一次函数y=ax+a可知,一次函数的图象与x轴交于点(-1,0),排除A,B项.
当a>0时,二次函数的图象开口向上,一次函数的图象经过第一、二、三象限,D项符合.
当a<0时,二次函数的图象开口向下,一次函数的图象经过第二、三、四象限,排除C项.
故答案选D.
解析
由一次函数y=ax+a可知,一次函数的图象与x轴交于点(-1,0),排除A,B项.
当a>0时,二次函数的图象开口向上,一次函数的图象经过第一、二、三象限,D项符合.
当a<0时,二次函数的图象开口向下,一次函数的图象经过第二、三、四象限,排除C项.
故答案选D.
点拨
解此类题除了逐项判断外,较简捷的方法是按照字母系数的正负分情况讨论,直接选出符合某种情况的图象.
