2019-2020学年吉林省第二实验中学九年级(下)第三次月考数学试题(word版含答案)
文档属性
| 名称 | 2019-2020学年吉林省第二实验中学九年级(下)第三次月考数学试题(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 698.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-22 17:08:57 | ||
图片预览




文档简介
2019-2020学年吉林省第二实验中学九年级(下)第三次月考
一、选择题(本大题共8小题,每小题3分,共24分)
1.下列有理数中最小的是( )
A.﹣1
B.﹣2
C.3
D.0
2.习近平总书记提出了未来5年“精准扶贫”的战略构想,意味着每年要减贫约11700000人,将数据11700000用科学记数法表示为( )
A.1.17×106
B.1.17×107
C.1.17×108
D.11.7×106
3.分别从正面和上面观察长方体的形状,如图所示(单位:m),则从左面观察此长方体,看到的图形的面积是( )
A.4m2
B.12m2
C.1m2
D.3m2
4.下列运算中正确的是( )
A.3a+2b=5ab
B.2a2+3a2=5a5
C.a10÷a5=a2
D.(xy2)3=x3y6
5.如图,在△CEF中,∠E=80°,∠F=50°,AB∥CF,AD∥CE,连接BC,CD,则∠A的度数是( )
A.45°
B.50°
C.55°
D.80°
6.如图,∠MAN=60°,点B为AM上一点,以点A为圆心、任意长为半径画弧,交AM于点E,交AN于点D.再分别以点D,E为圆心、大于DE的长为半径画弧,两弧交于点F.作射线AF,在AF上取点G,连接BG,过点G作GC⊥AN,垂足为点C.若AG=6,则BG的长可能为( )
A.1
B.2
C.
D.2
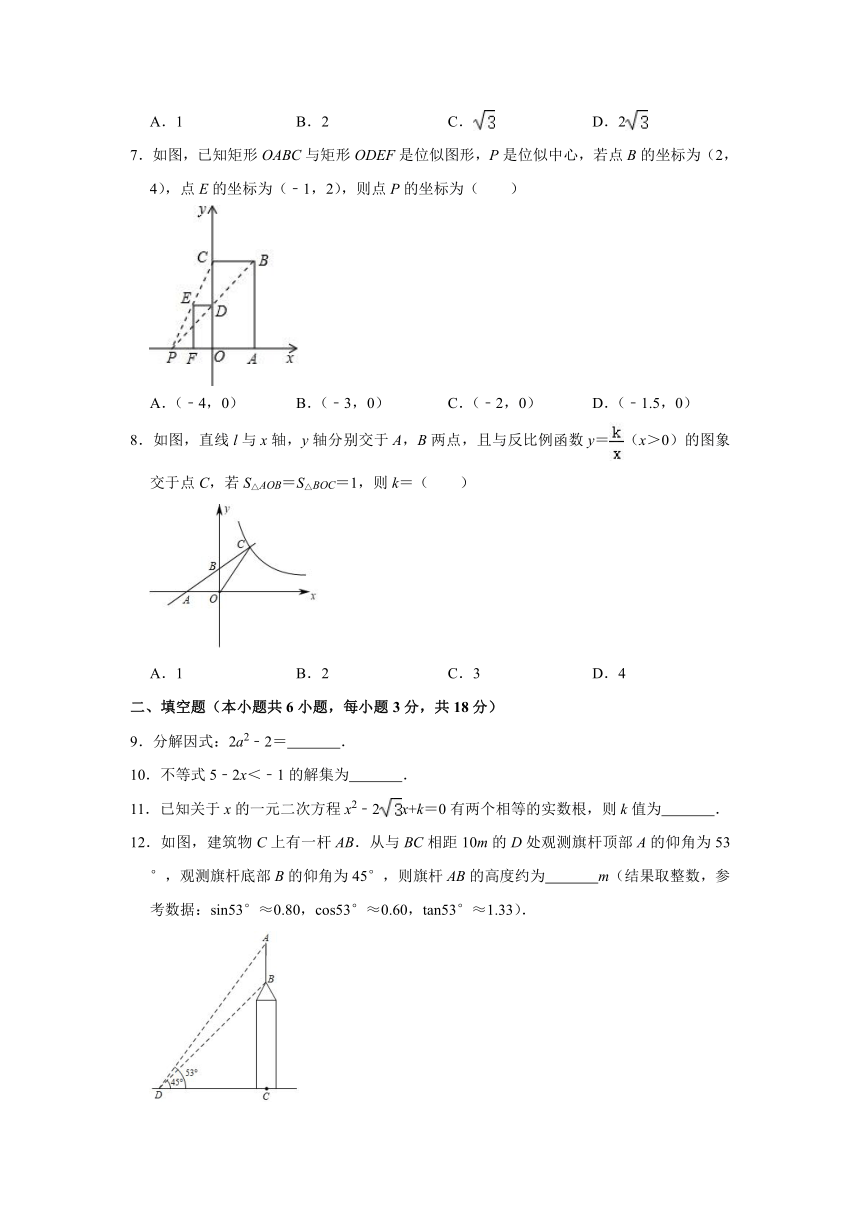
7.如图,已知矩形OABC与矩形ODEF是位似图形,P是位似中心,若点B的坐标为(2,4),点E的坐标为(﹣1,2),则点P的坐标为( )
A.(﹣4,0)
B.(﹣3,0)
C.(﹣2,0)
D.(﹣1.5,0)
8.如图,直线l与x轴,y轴分别交于A,B两点,且与反比例函数y=(x>0)的图象交于点C,若S△AOB=S△BOC=1,则k=( )
A.1
B.2
C.3
D.4
二、填空题(本小题共6小题,每小题3分,共18分)
9.分解因式:2a2﹣2=
.
10.不等式5﹣2x<﹣1的解集为
.
11.已知关于x的一元二次方程x2﹣2x+k=0有两个相等的实数根,则k值为
.
12.如图,建筑物C上有一杆AB.从与BC相距10m的D处观测旗杆顶部A的仰角为53°,观测旗杆底部B的仰角为45°,则旗杆AB的高度约为
m(结果取整数,参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33).
13.如图,在Rt△ABC中,∠BAC=90°,且BA=9,AC=12,点D是斜边BC上的一个动点,过点D分别作DE⊥AB于点E,DF⊥AC于点F,点G为四边形DEAF对角线交点,则线段GF的最小值为
.
14.定义:在平面直角坐标系中,若点A满足横、纵坐标都为整数,则把点A叫做“整点”.如:B(3,0)、C(﹣1,3)都是“整点”.抛物线y=ax2﹣2ax+a+2(a<0)与x轴交于点M,N两点,若该抛物线在M、N之间的部分与线段MN所围的区域(包括边界)恰有5个整点,则a的取值范围是
.
三、解答题(本大题共10小题,共78分)
15.先化简(x+3﹣)÷,再从0≤x≤4中选一个适合的整数代入求值.
16.“新冠肺炎”肆虐,无数抗疫英雄涌现,以下四位抗疫英雄是钟南山、李兰娟、李文亮、张定宇(依次记为A、B、C、D).为让同学们了解四位的事迹,老师设计如下活动:取四张完全相同的卡片,分别写上A、B、C、D四个标号,然后背面朝上放置,搅匀后每个同学从中随机抽取一张,记下标号后放回,老师要求每位同学依据抽到的卡片上的标号查找相应抗疫英雄的资料,并做成小报.
(1)班长在四种卡片中随机抽到标号为C的概率为
.
(2)平平和安安两位同学抽到的卡片是不同英雄的概率是多少?用树状图或列表的方法表示.
17.新冠肺炎疫情期间,某小区计划购买甲、乙两种品牌的消毒剂,乙品牌消毒剂每瓶的价格比甲品牌消毒剂每瓶价格的3倍少50元,已知用300元购买甲品牌消毒剂的数量与用400元购买乙品牌消毒剂的数量相同.求甲、乙两种品牌消毒剂每瓶的价格各是多少元?
18.如图1,在△ABC中,AC=BC,以BC为直径的⊙O交AB于点D.
(1)求证:点D是AB的中点;
(2)如图2,过点D作DE⊥AC于点E,求证:DE是⊙O的切线.
19.图中的每个小方格都是边长为1的正方形,A、O、B都在格点上,请在网格纸中完成.
(1)作出图中∠AOB的平分线OP.
(2)在格点上找到一点Q,连接OQ,使得tan∠POQ=.
20.在推进城乡生活垃圾分类的行动中,某社区为了了解居民掌握垃圾分类知识的情况进行调查.其中A、B两小区分别有500名居民参加了测试,社区从中各随机抽取50名居民成绩进行整理得到部分信息:
[信息一]A小区50名居民成绩的频数直方图如图(每一组含前一个边界值,不含后一个边界值):
[信息二]如图中,丛左往右第四组的成绩如下:
75,75,79,79,79,79,80,80,81,82,82,83,83,84,84,84
[信息三]A、B两小区各50名居民成绩的平均数、中位数、众数、优秀率(80分及以上为优秀)、方差等数据如表(部分空缺):
小区
平均数
中位数
众数
优秀率
方差
A
75.1
79
40%
277
B
75.1
77
76
45%
211
根据以上信息,回答下列问题:
(1)A小区50名居民成绩的中位数是
.
(2)两个小区中居民成绩更稳定的是
(填“A”或“B”)小区.
(3)请估计A小区500名居民成绩能超过平均数的人数.
21.某市制米厂接到加工大米任务,要求5天内加工完220吨大米,制米厂安排甲、乙两车间共同完成加工任务,乙车间加工中途停工一段时间维修设备,然后改变加工效率继续加工,直到与甲车间同时完成加工任务为止.甲、乙两车间各自加工大米数量y(吨)与甲车间加工时间x(天)之间的关系如图(1)所示;未加工大米w(吨)与甲加工时间x(天)之间的关系如图(2)所示,请结合图象回答下列问题:
(1)甲车间每天加工大米
吨,a=
.
(2)求乙车间维修设备后,乙车间加工大米数量y(吨)与x(天)之间函数关系式.
(3)若55吨大米恰好装满一节车厢,那么加工多长时间装满第一节车厢?再加工多长时间恰好装满第二节车厢?
22.[问题重现]观察图①,当点P与点Q位于直线AB同侧时,过点P作PD⊥AB于点D,过点Q作QE⊥AB交AB延长线于点E,则=
(用图中已有线段表示).这个问题不难解答,因为三角形的面积等于底乘以高除以2,显然两个三角形共底,面积之比就等于高之比,∴=.
[模型变式]如图①,点P与点Q位于直线AB两侧时,延长AB交PQ于点M,则在图中=
(用图中已有线段表示),并证明你的结论.
[简单应用]如图③,点P是△ABC内部一点,且AP平分∠CAB,连接CP并延长交AB于点M,当CM⊥AP时,且△ABC的面积为16,则△APB的面积为
.
[灵活运用]如图④,O是线段AD上一点(不与点A、D重合),连接BO并延长交AC于点F,连接CO并延长交AB于点E.已知线段OD=2,AD=6,OE=2,EC=8,OF=4,则BF=
.
23.已知二次函数C1:y1=x2+2mx+2m2﹣3与C2:y2=x2﹣4mx+4m2﹣m﹣1.
(1)当两个函数有相同的最小值时,求m的值.
(2)当﹣2≤x≤2时,是否存在相应的m,使得两个函数的最小值相等,如果存在,求出m的值,不存在,说明理由.
(3)定义一个新的函数y,当x≤﹣1时,y=x2+2mx+2m2﹣3;当x>﹣1时,y=x2﹣4mx+4m2﹣m﹣1,已知当﹣2≤x≤2时,存在一条直线y=t(﹣2≤t≤﹣1),使它与函数y有三个交点,直接写出m的取值范围.
24.如图,在菱形ABCD中,AB=5,tan∠DAB=,连接对角线AC、BD.点P从A出发,以每秒个单位的速度沿AC向终点C运动.过点P作PH垂直AB交AB于点H.作点P关于直线BD的对称点Q,连接HQ.
(1)用含t的代数式表示PQ长.
(2)以P、B、Q、D为顶点的四边形是正方形时,求出此时t的值.
(3)设△PQH的面积为S,求S与t的函数关系式.
(4)作点P关于直线AB的对称点R,连接QR,当QR与菱形ABCD的边平行或垂直时,直接写出t的值.
参考答案与试题解析
1-5.BBDDB
6-8.DCD
9.2(a+1)(a﹣1)
10.x>3
11.3
12.3
13.
14.﹣2≤a<﹣1
15.解:(x+3﹣)÷
=(﹣)÷
=?
=,
当x=1时,原式==.
16.解:(1)∵共有四张卡片,分别是A、B、C、D四个标号,
∴班长在四种卡片中随机抽到标号为C的概率是;
故答案为:;
(2)根据题意画树状图如下:
共有16种等可能的结果数,其中平平和安安两位同学抽到的卡片是不同英雄的有12种结果,
则平平和安安两位同学抽到的卡片是不同英雄的概率为=.
17.解:设甲品牌消毒剂每瓶的价格为x元;乙品牌消毒剂每瓶的价格为(3x﹣50)元,
由题意得:=,
解得:x=30,
经检验,x=30是原方程的解且符合实际意义,
3x﹣5═40,
答:甲品牌消毒剂每瓶的价格为30元;乙品牌消毒剂每瓶的价格为40元.
18.证明:(1)如图1,连接CD,
∵BC为⊙O的直径,
∴CD⊥AB.
∵AC=BC,
∴AD=BD.
(2)如图2,连接OD;
∵AD=BD,OB=OC,
∴OD是△BCA的中位线,
∴OD∥AC.
∵DE⊥AC,
∴DF⊥OD.
∵OD为半径,
∴DE是⊙O的切线.
19.解:(1)如图所示:OP即为所求;
(2)如图所示:点Q即为所求,tan∠POQ=.
20.解:(1)A小区50名居民成绩的中位数是=75(分),
(2)∵=277,=211,
∴<,
∴两个小区中居民成绩更稳定的是B小区,
故答案为:B;
(3)估计A小区500名居民成绩能超过平均数的人数为500×=240(人).
21.解:(1)由图象可知,第一天甲乙共加工220﹣185=35吨,第二天,乙停止工作,甲单独加工185﹣165=20吨,
则乙一天加工35﹣20=15吨.a=15
故答案为:20,15
(2)设y=kx+b
把(2,15),(5,120)代入
解得
∴y=35x﹣55
(3)由图2可知
当w=220﹣55=165时,恰好是第二天加工结束.
当2≤x≤5时,两个车间每天加工速度为=55吨
∴再过1天装满第二节车厢
22.解:[问题重现]
∵S△PAB=AB?PD,S△QAB=AB?QE,∴.
[模型变式].
证明:过点P作PD⊥AM,交AM延长线于点D,过点Q作QE⊥AM交AM于点E,
则QE∥PD,
∴△PDM∽△QEM,
∴,
由[问题重现]可知,
∴.
故答案为:.
[简单应用]过点P作PD⊥AB于点D,过点C作CE⊥AB于点E,
则CE∥PD,
∵AP平分∠CAB,
∴∠CAP=∠MAP,
∵CM⊥AP,
∴∠APC=∠APM=90°,
又∵AP=AP,
∴△APC≌△APM(ASA),
∴CP=PM,
∴MD=DE,
∴PD=CE,
∴,
∵△ABC的面积为16,
∴△APB的面积为8.
[灵活运用]
由[简单应用]得,,,
∴===1.
∵OD=2,AD=6,OE=2,EC=8,OF=4,
∴=1.
解得BF=.
23.解:(1)y1=x2+2mx+2m2﹣3=(x+m)2+m2﹣3,
y2=x2﹣4mx+4m2﹣m﹣1=(x﹣2m)2﹣m﹣1,
∴两条抛物线的顶点坐标分别是(﹣m,m2﹣3)和(2m,﹣m﹣1),
∵y1与y2有相同的最小值,
∴m2﹣3=﹣m﹣1,
解得m=1或m=﹣2.
(2)存在.
设抛物线C1的顶点为M1,抛物线C2的顶点为M2.
①当﹣1≤m≤1时,如图1,M1、M2都在直线x=﹣2和x=2之间,
由(1)得两个函数的最小值相等时m=1;
②当﹣2≤m<﹣1时,如图2,抛物线C2过点A(﹣2,4m2+7m+3),
若两个函数的最小值相等,则4m2+7m+3=m2﹣3,此方程无解;
当1<m≤2时,如图3,抛物线C2过点B(2,4m2﹣9m+3),
若两个函数的最小值相等,则4m2﹣9m+3=m2﹣3,
解得m=2或m=1(舍去)
③当m<﹣2时,如图4,抛物线C1过点C(2,2m2+4m+1),
若两个函数的最小值相等,则4m2+7m+3=2m2+4m+1,此方程无解;
当m>2时,如图5,抛物线C1过点D(﹣2,2m2﹣4+1),
若两个函数的最小值相等,则4m2﹣9m+3=2m2﹣4+1,
解得m=(舍去),或m=2(舍去).
综上所述,m=1或m=2.
(3)①如图6,当m≤0时,不存在符合条件的三个公共点;
②当m>0,且M2在直线y=﹣2上方时,存在符合条件的三个公共点,如图7,
则,解得0<m<1;
③当m=1时,如图8,m2﹣3=﹣2,﹣m﹣1=﹣2,
∴M1、M2分别为直线x=﹣1与直线y=﹣2的交点、直线x=﹣2与直线的交点,
此时不存在符合条件的三个公共点,∴m≠1.
④当m>1时,如图9,需满足顶点M1在直线y=﹣2和y=﹣1之间,
∴,
解得1<m<.
⑤当m≥时,如图10,不存在符合条件的三个公共点.
综上所述,0<m<1或1<m<.
24.解:(1)如图1中,过点D作DM⊥AB于M.
∵tan∠DAM==,AD=AB=5,
∴DM=4,AM=3,
∴BM=AB﹣AM=5﹣3=2,
∴BD===2,
∵四边形ABCD是菱形,
∴OA=OC,OB=OD=,AC⊥BD,
∴∠AOB=90°,
∴OA===2,
∴当0≤t<2时,PQ=2OP=2(2﹣t)=4﹣2t.
当2≤t≤4时,PQ=2OP=2(t﹣2)=2t﹣4.
(2)如图2中,连接PD,BP,BQ,DQ.
当OP=OD时,以P、B、Q、D为顶点的四边形是正方形,
∴|2﹣t|=,
解得t=1或3.
(3)如图3﹣1中,当0<t<2时,过点H作HJ⊥AC于J.
在Rt△APH中,AH=AP?cos∠PAB=t?=2t,HJ=AH?sin∠PAB=2t?=t,
S=?PQ?HJ=?(4﹣2t)?t=﹣2t2+4t,
当2<t≤4时,如图3﹣2中,S=?PQ?HJ=?(2t﹣4)?t=2t2﹣4t,
综上所述,S=.
(4)如图4﹣1中,当QR∥AD时,过点D作DM⊥AB于M交AO于J.
由题意OJ=DO?tan∠BDM=,DJ===,AJ=AO=OJ=,
∵AB∥QR,
∴∠DAQ=∠AQR,
∵DM⊥AB,PR⊥AB,
∴PR∥DM,
∴∠AJD=∠QPR,
∴△AJD∽△QPR,
∴=,
∴=,
解得t=.
如图4﹣2中,当P,Q与O重合时,QR⊥AB,此时t=2.
如图4﹣3中,当RQ⊥AD时,延长RQ交AD于T.
∵PR⊥AB,DM⊥AB,
∴DM∥PR,
∴∠RPQ=∠DJO,
∵四边形ABCD是菱形,
∴∠DAC=∠BAC,
∵∠DOJ=∠AMJ=90°,∠DJO=∠AJM,
∴∠ODJ=∠JAM=∠DAC,
∵∠DAC+∠AQT=90°,∠ODJ+∠DJO=90°,
∴∠AOT=∠DJO,
∵∠RQP=∠AQT,
∴∠RQP=∠DJO=∠RPQ,
∴RP=RQ,
∵BO垂直平分线段PQ,
∴O,B,R共线,
∴cos∠OPR=cos∠DJO,
∴=,
∴=,
∴t=,
综上所述,满足条件的t的值为或2或.
一、选择题(本大题共8小题,每小题3分,共24分)
1.下列有理数中最小的是( )
A.﹣1
B.﹣2
C.3
D.0
2.习近平总书记提出了未来5年“精准扶贫”的战略构想,意味着每年要减贫约11700000人,将数据11700000用科学记数法表示为( )
A.1.17×106
B.1.17×107
C.1.17×108
D.11.7×106
3.分别从正面和上面观察长方体的形状,如图所示(单位:m),则从左面观察此长方体,看到的图形的面积是( )
A.4m2
B.12m2
C.1m2
D.3m2
4.下列运算中正确的是( )
A.3a+2b=5ab
B.2a2+3a2=5a5
C.a10÷a5=a2
D.(xy2)3=x3y6
5.如图,在△CEF中,∠E=80°,∠F=50°,AB∥CF,AD∥CE,连接BC,CD,则∠A的度数是( )
A.45°
B.50°
C.55°
D.80°
6.如图,∠MAN=60°,点B为AM上一点,以点A为圆心、任意长为半径画弧,交AM于点E,交AN于点D.再分别以点D,E为圆心、大于DE的长为半径画弧,两弧交于点F.作射线AF,在AF上取点G,连接BG,过点G作GC⊥AN,垂足为点C.若AG=6,则BG的长可能为( )
A.1
B.2
C.
D.2
7.如图,已知矩形OABC与矩形ODEF是位似图形,P是位似中心,若点B的坐标为(2,4),点E的坐标为(﹣1,2),则点P的坐标为( )
A.(﹣4,0)
B.(﹣3,0)
C.(﹣2,0)
D.(﹣1.5,0)
8.如图,直线l与x轴,y轴分别交于A,B两点,且与反比例函数y=(x>0)的图象交于点C,若S△AOB=S△BOC=1,则k=( )
A.1
B.2
C.3
D.4
二、填空题(本小题共6小题,每小题3分,共18分)
9.分解因式:2a2﹣2=
.
10.不等式5﹣2x<﹣1的解集为
.
11.已知关于x的一元二次方程x2﹣2x+k=0有两个相等的实数根,则k值为
.
12.如图,建筑物C上有一杆AB.从与BC相距10m的D处观测旗杆顶部A的仰角为53°,观测旗杆底部B的仰角为45°,则旗杆AB的高度约为
m(结果取整数,参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33).
13.如图,在Rt△ABC中,∠BAC=90°,且BA=9,AC=12,点D是斜边BC上的一个动点,过点D分别作DE⊥AB于点E,DF⊥AC于点F,点G为四边形DEAF对角线交点,则线段GF的最小值为
.
14.定义:在平面直角坐标系中,若点A满足横、纵坐标都为整数,则把点A叫做“整点”.如:B(3,0)、C(﹣1,3)都是“整点”.抛物线y=ax2﹣2ax+a+2(a<0)与x轴交于点M,N两点,若该抛物线在M、N之间的部分与线段MN所围的区域(包括边界)恰有5个整点,则a的取值范围是
.
三、解答题(本大题共10小题,共78分)
15.先化简(x+3﹣)÷,再从0≤x≤4中选一个适合的整数代入求值.
16.“新冠肺炎”肆虐,无数抗疫英雄涌现,以下四位抗疫英雄是钟南山、李兰娟、李文亮、张定宇(依次记为A、B、C、D).为让同学们了解四位的事迹,老师设计如下活动:取四张完全相同的卡片,分别写上A、B、C、D四个标号,然后背面朝上放置,搅匀后每个同学从中随机抽取一张,记下标号后放回,老师要求每位同学依据抽到的卡片上的标号查找相应抗疫英雄的资料,并做成小报.
(1)班长在四种卡片中随机抽到标号为C的概率为
.
(2)平平和安安两位同学抽到的卡片是不同英雄的概率是多少?用树状图或列表的方法表示.
17.新冠肺炎疫情期间,某小区计划购买甲、乙两种品牌的消毒剂,乙品牌消毒剂每瓶的价格比甲品牌消毒剂每瓶价格的3倍少50元,已知用300元购买甲品牌消毒剂的数量与用400元购买乙品牌消毒剂的数量相同.求甲、乙两种品牌消毒剂每瓶的价格各是多少元?
18.如图1,在△ABC中,AC=BC,以BC为直径的⊙O交AB于点D.
(1)求证:点D是AB的中点;
(2)如图2,过点D作DE⊥AC于点E,求证:DE是⊙O的切线.
19.图中的每个小方格都是边长为1的正方形,A、O、B都在格点上,请在网格纸中完成.
(1)作出图中∠AOB的平分线OP.
(2)在格点上找到一点Q,连接OQ,使得tan∠POQ=.
20.在推进城乡生活垃圾分类的行动中,某社区为了了解居民掌握垃圾分类知识的情况进行调查.其中A、B两小区分别有500名居民参加了测试,社区从中各随机抽取50名居民成绩进行整理得到部分信息:
[信息一]A小区50名居民成绩的频数直方图如图(每一组含前一个边界值,不含后一个边界值):
[信息二]如图中,丛左往右第四组的成绩如下:
75,75,79,79,79,79,80,80,81,82,82,83,83,84,84,84
[信息三]A、B两小区各50名居民成绩的平均数、中位数、众数、优秀率(80分及以上为优秀)、方差等数据如表(部分空缺):
小区
平均数
中位数
众数
优秀率
方差
A
75.1
79
40%
277
B
75.1
77
76
45%
211
根据以上信息,回答下列问题:
(1)A小区50名居民成绩的中位数是
.
(2)两个小区中居民成绩更稳定的是
(填“A”或“B”)小区.
(3)请估计A小区500名居民成绩能超过平均数的人数.
21.某市制米厂接到加工大米任务,要求5天内加工完220吨大米,制米厂安排甲、乙两车间共同完成加工任务,乙车间加工中途停工一段时间维修设备,然后改变加工效率继续加工,直到与甲车间同时完成加工任务为止.甲、乙两车间各自加工大米数量y(吨)与甲车间加工时间x(天)之间的关系如图(1)所示;未加工大米w(吨)与甲加工时间x(天)之间的关系如图(2)所示,请结合图象回答下列问题:
(1)甲车间每天加工大米
吨,a=
.
(2)求乙车间维修设备后,乙车间加工大米数量y(吨)与x(天)之间函数关系式.
(3)若55吨大米恰好装满一节车厢,那么加工多长时间装满第一节车厢?再加工多长时间恰好装满第二节车厢?
22.[问题重现]观察图①,当点P与点Q位于直线AB同侧时,过点P作PD⊥AB于点D,过点Q作QE⊥AB交AB延长线于点E,则=
(用图中已有线段表示).这个问题不难解答,因为三角形的面积等于底乘以高除以2,显然两个三角形共底,面积之比就等于高之比,∴=.
[模型变式]如图①,点P与点Q位于直线AB两侧时,延长AB交PQ于点M,则在图中=
(用图中已有线段表示),并证明你的结论.
[简单应用]如图③,点P是△ABC内部一点,且AP平分∠CAB,连接CP并延长交AB于点M,当CM⊥AP时,且△ABC的面积为16,则△APB的面积为
.
[灵活运用]如图④,O是线段AD上一点(不与点A、D重合),连接BO并延长交AC于点F,连接CO并延长交AB于点E.已知线段OD=2,AD=6,OE=2,EC=8,OF=4,则BF=
.
23.已知二次函数C1:y1=x2+2mx+2m2﹣3与C2:y2=x2﹣4mx+4m2﹣m﹣1.
(1)当两个函数有相同的最小值时,求m的值.
(2)当﹣2≤x≤2时,是否存在相应的m,使得两个函数的最小值相等,如果存在,求出m的值,不存在,说明理由.
(3)定义一个新的函数y,当x≤﹣1时,y=x2+2mx+2m2﹣3;当x>﹣1时,y=x2﹣4mx+4m2﹣m﹣1,已知当﹣2≤x≤2时,存在一条直线y=t(﹣2≤t≤﹣1),使它与函数y有三个交点,直接写出m的取值范围.
24.如图,在菱形ABCD中,AB=5,tan∠DAB=,连接对角线AC、BD.点P从A出发,以每秒个单位的速度沿AC向终点C运动.过点P作PH垂直AB交AB于点H.作点P关于直线BD的对称点Q,连接HQ.
(1)用含t的代数式表示PQ长.
(2)以P、B、Q、D为顶点的四边形是正方形时,求出此时t的值.
(3)设△PQH的面积为S,求S与t的函数关系式.
(4)作点P关于直线AB的对称点R,连接QR,当QR与菱形ABCD的边平行或垂直时,直接写出t的值.
参考答案与试题解析
1-5.BBDDB
6-8.DCD
9.2(a+1)(a﹣1)
10.x>3
11.3
12.3
13.
14.﹣2≤a<﹣1
15.解:(x+3﹣)÷
=(﹣)÷
=?
=,
当x=1时,原式==.
16.解:(1)∵共有四张卡片,分别是A、B、C、D四个标号,
∴班长在四种卡片中随机抽到标号为C的概率是;
故答案为:;
(2)根据题意画树状图如下:
共有16种等可能的结果数,其中平平和安安两位同学抽到的卡片是不同英雄的有12种结果,
则平平和安安两位同学抽到的卡片是不同英雄的概率为=.
17.解:设甲品牌消毒剂每瓶的价格为x元;乙品牌消毒剂每瓶的价格为(3x﹣50)元,
由题意得:=,
解得:x=30,
经检验,x=30是原方程的解且符合实际意义,
3x﹣5═40,
答:甲品牌消毒剂每瓶的价格为30元;乙品牌消毒剂每瓶的价格为40元.
18.证明:(1)如图1,连接CD,
∵BC为⊙O的直径,
∴CD⊥AB.
∵AC=BC,
∴AD=BD.
(2)如图2,连接OD;
∵AD=BD,OB=OC,
∴OD是△BCA的中位线,
∴OD∥AC.
∵DE⊥AC,
∴DF⊥OD.
∵OD为半径,
∴DE是⊙O的切线.
19.解:(1)如图所示:OP即为所求;
(2)如图所示:点Q即为所求,tan∠POQ=.
20.解:(1)A小区50名居民成绩的中位数是=75(分),
(2)∵=277,=211,
∴<,
∴两个小区中居民成绩更稳定的是B小区,
故答案为:B;
(3)估计A小区500名居民成绩能超过平均数的人数为500×=240(人).
21.解:(1)由图象可知,第一天甲乙共加工220﹣185=35吨,第二天,乙停止工作,甲单独加工185﹣165=20吨,
则乙一天加工35﹣20=15吨.a=15
故答案为:20,15
(2)设y=kx+b
把(2,15),(5,120)代入
解得
∴y=35x﹣55
(3)由图2可知
当w=220﹣55=165时,恰好是第二天加工结束.
当2≤x≤5时,两个车间每天加工速度为=55吨
∴再过1天装满第二节车厢
22.解:[问题重现]
∵S△PAB=AB?PD,S△QAB=AB?QE,∴.
[模型变式].
证明:过点P作PD⊥AM,交AM延长线于点D,过点Q作QE⊥AM交AM于点E,
则QE∥PD,
∴△PDM∽△QEM,
∴,
由[问题重现]可知,
∴.
故答案为:.
[简单应用]过点P作PD⊥AB于点D,过点C作CE⊥AB于点E,
则CE∥PD,
∵AP平分∠CAB,
∴∠CAP=∠MAP,
∵CM⊥AP,
∴∠APC=∠APM=90°,
又∵AP=AP,
∴△APC≌△APM(ASA),
∴CP=PM,
∴MD=DE,
∴PD=CE,
∴,
∵△ABC的面积为16,
∴△APB的面积为8.
[灵活运用]
由[简单应用]得,,,
∴===1.
∵OD=2,AD=6,OE=2,EC=8,OF=4,
∴=1.
解得BF=.
23.解:(1)y1=x2+2mx+2m2﹣3=(x+m)2+m2﹣3,
y2=x2﹣4mx+4m2﹣m﹣1=(x﹣2m)2﹣m﹣1,
∴两条抛物线的顶点坐标分别是(﹣m,m2﹣3)和(2m,﹣m﹣1),
∵y1与y2有相同的最小值,
∴m2﹣3=﹣m﹣1,
解得m=1或m=﹣2.
(2)存在.
设抛物线C1的顶点为M1,抛物线C2的顶点为M2.
①当﹣1≤m≤1时,如图1,M1、M2都在直线x=﹣2和x=2之间,
由(1)得两个函数的最小值相等时m=1;
②当﹣2≤m<﹣1时,如图2,抛物线C2过点A(﹣2,4m2+7m+3),
若两个函数的最小值相等,则4m2+7m+3=m2﹣3,此方程无解;
当1<m≤2时,如图3,抛物线C2过点B(2,4m2﹣9m+3),
若两个函数的最小值相等,则4m2﹣9m+3=m2﹣3,
解得m=2或m=1(舍去)
③当m<﹣2时,如图4,抛物线C1过点C(2,2m2+4m+1),
若两个函数的最小值相等,则4m2+7m+3=2m2+4m+1,此方程无解;
当m>2时,如图5,抛物线C1过点D(﹣2,2m2﹣4+1),
若两个函数的最小值相等,则4m2﹣9m+3=2m2﹣4+1,
解得m=(舍去),或m=2(舍去).
综上所述,m=1或m=2.
(3)①如图6,当m≤0时,不存在符合条件的三个公共点;
②当m>0,且M2在直线y=﹣2上方时,存在符合条件的三个公共点,如图7,
则,解得0<m<1;
③当m=1时,如图8,m2﹣3=﹣2,﹣m﹣1=﹣2,
∴M1、M2分别为直线x=﹣1与直线y=﹣2的交点、直线x=﹣2与直线的交点,
此时不存在符合条件的三个公共点,∴m≠1.
④当m>1时,如图9,需满足顶点M1在直线y=﹣2和y=﹣1之间,
∴,
解得1<m<.
⑤当m≥时,如图10,不存在符合条件的三个公共点.
综上所述,0<m<1或1<m<.
24.解:(1)如图1中,过点D作DM⊥AB于M.
∵tan∠DAM==,AD=AB=5,
∴DM=4,AM=3,
∴BM=AB﹣AM=5﹣3=2,
∴BD===2,
∵四边形ABCD是菱形,
∴OA=OC,OB=OD=,AC⊥BD,
∴∠AOB=90°,
∴OA===2,
∴当0≤t<2时,PQ=2OP=2(2﹣t)=4﹣2t.
当2≤t≤4时,PQ=2OP=2(t﹣2)=2t﹣4.
(2)如图2中,连接PD,BP,BQ,DQ.
当OP=OD时,以P、B、Q、D为顶点的四边形是正方形,
∴|2﹣t|=,
解得t=1或3.
(3)如图3﹣1中,当0<t<2时,过点H作HJ⊥AC于J.
在Rt△APH中,AH=AP?cos∠PAB=t?=2t,HJ=AH?sin∠PAB=2t?=t,
S=?PQ?HJ=?(4﹣2t)?t=﹣2t2+4t,
当2<t≤4时,如图3﹣2中,S=?PQ?HJ=?(2t﹣4)?t=2t2﹣4t,
综上所述,S=.
(4)如图4﹣1中,当QR∥AD时,过点D作DM⊥AB于M交AO于J.
由题意OJ=DO?tan∠BDM=,DJ===,AJ=AO=OJ=,
∵AB∥QR,
∴∠DAQ=∠AQR,
∵DM⊥AB,PR⊥AB,
∴PR∥DM,
∴∠AJD=∠QPR,
∴△AJD∽△QPR,
∴=,
∴=,
解得t=.
如图4﹣2中,当P,Q与O重合时,QR⊥AB,此时t=2.
如图4﹣3中,当RQ⊥AD时,延长RQ交AD于T.
∵PR⊥AB,DM⊥AB,
∴DM∥PR,
∴∠RPQ=∠DJO,
∵四边形ABCD是菱形,
∴∠DAC=∠BAC,
∵∠DOJ=∠AMJ=90°,∠DJO=∠AJM,
∴∠ODJ=∠JAM=∠DAC,
∵∠DAC+∠AQT=90°,∠ODJ+∠DJO=90°,
∴∠AOT=∠DJO,
∵∠RQP=∠AQT,
∴∠RQP=∠DJO=∠RPQ,
∴RP=RQ,
∵BO垂直平分线段PQ,
∴O,B,R共线,
∴cos∠OPR=cos∠DJO,
∴=,
∴=,
∴t=,
综上所述,满足条件的t的值为或2或.
同课章节目录
