2021-2022学年北师大版九年级数学上册第三章概率的进一步认识——概率的综合应用章末专题练习题(Word版,含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学上册第三章概率的进一步认识——概率的综合应用章末专题练习题(Word版,含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 202.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-22 23:16:50 | ||
图片预览


文档简介
2021-2022学年北师大版九年级数学上册第三章
概率的综合应用
章末专题练习题
类型1 概率与数、式的综合
1.在盒子里放有分别写有整式2,π,x,x+1的四张卡片,从中随机抽取两张,把卡片上的整式分别作为分子和分母,则能组成分式的概率是(
)
A.
B.
C.
D.
类型2 概率与方程、不等式的综合
2.如果m是从-2,-1,0,1四个数中任取的一个数,那么关于x的方程=+1的根为正数的概率为____.
3.有六张正面分别标有数字-1,0,1,2,3,4的不透明卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中任取一张,则抽取的卡片上的数字为不等式组的解的概率为____.
4.有9张卡片,分别写有1~9这九个数字,将它们背面朝上洗匀后,任意抽出一张,记卡片上的数字为a,则关于x的不等式组有解的概率为____.
类型3 概率与函数的综合
5.从数-2,-1,4中随机抽取一个数记为m,再从数2,1,-4中随机抽取一个数记为n,则一次函数y=mnx中y的值随x的增大而减小的概率是____.
6.如图,把一个转盘分成四等份,依次标上数字1,2,3,4.若连续自由转动转盘两次,指针指向的数字分别记作a,b,作为点A的横、纵坐标,则点A(a,b)在函数y=2x的图象上的概率为____.
7.四个完全相同的小球上分别标有数字-2,-1,1,3,从这4个球中任意取出一个球记为a,不放回,再取出一个记为b,则能使一次函数y=2ax+b的图象必过第一、四象限的概率为____.
类型4 概率与几何的综合
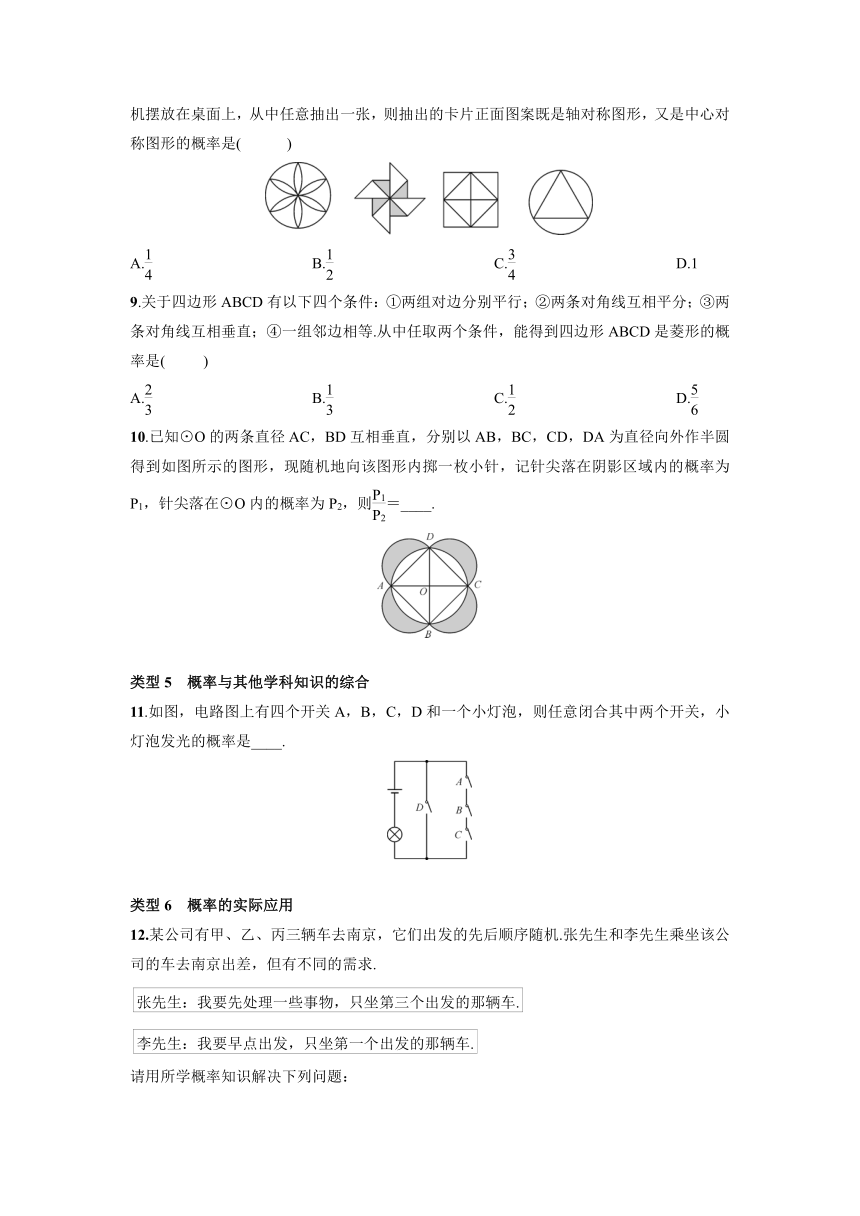
8.四张质地、大小、背面完全相同的卡片上,正面分别画有下列图案,现把它们正面朝下随机摆放在桌面上,从中任意抽出一张,则抽出的卡片正面图案既是轴对称图形,又是中心对称图形的概率是(
)
A.
B.
C.
D.1
9.关于四边形ABCD有以下四个条件:①两组对边分别平行;②两条对角线互相平分;③两条对角线互相垂直;④一组邻边相等.从中任取两个条件,能得到四边形ABCD是菱形的概率是(
)
A.
B.
C.
D.
10.已知⊙O的两条直径AC,BD互相垂直,分别以AB,BC,CD,DA为直径向外作半圆得到如图所示的图形,现随机地向该图形内掷一枚小针,记针尖落在阴影区域内的概率为P1,针尖落在⊙O内的概率为P2,则=____.
类型5 概率与其他学科知识的综合
11.如图,电路图上有四个开关A,B,C,D和一个小灯泡,则任意闭合其中两个开关,小灯泡发光的概率是____.
类型6 概率的实际应用
12.某公司有甲、乙、丙三辆车去南京,它们出发的先后顺序随机.张先生和李先生乘坐该公司的车去南京出差,但有不同的需求.
请用所学概率知识解决下列问题:
(1)写出这三辆车按先后顺序出发的所有可能结果.
(2)两人中,谁乘坐到甲车的可能性大?请说明理由.
13.“一方有难,八方支援”是中华民族的传统美德,在抗击新冠病毒战役中,某省为支援武汉,派出了由1
460人组成的医疗队.其中小丽、小王和三个同事共五人直接派往一线的同一家医院,根据该医院人事安排需要先抽出一人去急诊科,再派两人到该医院的发热门诊,请你利用所学知识完成下列问题.
(1)小丽被派往该院急诊科的概率是____.
(2)若正好抽出她们的一位同事去往急诊科,请你利用画树状图或列表的方法,求出小丽和小王同时被派往发热门诊的概率.
类型7 概率与统计的综合
14.2020年春节前夕“新型冠状病毒”爆发,疫情就是命令,防控就是使命.全国各地驰援武汉的医护工作者,践行医者仁心的使命与担当,舍小家,为大家,用自己的专业知识与血肉之躯构筑起全社会抗击疫情的钢铁长城.下面是2月9日当天全国部分省市驰援武汉医护工作者的人数统计图(不完整).
请解答下列问题:
(1)①上述省市2月9日当天驰援武汉的医护工作者的总人数为____人.
②请将条形统计图补充完整.
(2)请求出扇形统计图中“山东”所对应扇形的圆心角的度数.
(3)本次山东驰援武汉的医护工作者中,有5人报名去重症区,王医生和李医生就在其中,若从报名的5人中随机安排2人,求同时安排王医生和李医生去重症区的概率.
参考答案
2021-2022学年北师大版九年级数学上册第三章
概率的综合应用
章末专题练习题
类型1 概率与数、式的综合
1.在盒子里放有分别写有整式2,π,x,x+1的四张卡片,从中随机抽取两张,把卡片上的整式分别作为分子和分母,则能组成分式的概率是(
A
)
A.
B.
C.
D.
类型2 概率与方程、不等式的综合
2.如果m是从-2,-1,0,1四个数中任取的一个数,那么关于x的方程=+1的根为正数的概率为.
3.有六张正面分别标有数字-1,0,1,2,3,4的不透明卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中任取一张,则抽取的卡片上的数字为不等式组的解的概率为.
4.有9张卡片,分别写有1~9这九个数字,将它们背面朝上洗匀后,任意抽出一张,记卡片上的数字为a,则关于x的不等式组有解的概率为.
类型3 概率与函数的综合
5.从数-2,-1,4中随机抽取一个数记为m,再从数2,1,-4中随机抽取一个数记为n,则一次函数y=mnx中y的值随x的增大而减小的概率是.
6.如图,把一个转盘分成四等份,依次标上数字1,2,3,4.若连续自由转动转盘两次,指针指向的数字分别记作a,b,作为点A的横、纵坐标,则点A(a,b)在函数y=2x的图象上的概率为.
7.四个完全相同的小球上分别标有数字-2,-1,1,3,从这4个球中任意取出一个球记为a,不放回,再取出一个记为b,则能使一次函数y=2ax+b的图象必过第一、四象限的概率为.
类型4 概率与几何的综合
8.四张质地、大小、背面完全相同的卡片上,正面分别画有下列图案,现把它们正面朝下随机摆放在桌面上,从中任意抽出一张,则抽出的卡片正面图案既是轴对称图形,又是中心对称图形的概率是(
B
)
A.
B.
C.
D.1
9.关于四边形ABCD有以下四个条件:①两组对边分别平行;②两条对角线互相平分;③两条对角线互相垂直;④一组邻边相等.从中任取两个条件,能得到四边形ABCD是菱形的概率是(
A
)
A.
B.
C.
D.
10.已知⊙O的两条直径AC,BD互相垂直,分别以AB,BC,CD,DA为直径向外作半圆得到如图所示的图形,现随机地向该图形内掷一枚小针,记针尖落在阴影区域内的概率为P1,针尖落在⊙O内的概率为P2,则=.
类型5 概率与其他学科知识的综合
11.如图,电路图上有四个开关A,B,C,D和一个小灯泡,则任意闭合其中两个开关,小灯泡发光的概率是.
类型6 概率的实际应用
12.某公司有甲、乙、丙三辆车去南京,它们出发的先后顺序随机.张先生和李先生乘坐该公司的车去南京出差,但有不同的需求.
请用所学概率知识解决下列问题:
(1)写出这三辆车按先后顺序出发的所有可能结果.
(2)两人中,谁乘坐到甲车的可能性大?请说明理由.
解:(1)这三辆车按先后顺序出发的所有可能结果:
甲、乙、丙;甲、丙、乙;乙、甲、丙;乙、丙、甲;丙、甲、乙;丙、乙、甲;共6种.
(2)两人坐到甲车的可能性一样.理由:
由(1)可知张先生坐到甲车有两种可能:乙、丙、甲和丙、乙、甲,则张先生坐到甲车的概率是=.
由(1)可知李先生坐到甲车有两种可能:甲、乙、丙和甲、丙、乙,则李先生坐到甲车的概率是=.
所以两人坐到甲车的可能性一样.
13.“一方有难,八方支援”是中华民族的传统美德,在抗击新冠病毒战役中,某省为支援武汉,派出了由1
460人组成的医疗队.其中小丽、小王和三个同事共五人直接派往一线的同一家医院,根据该医院人事安排需要先抽出一人去急诊科,再派两人到该医院的发热门诊,请你利用所学知识完成下列问题.
(1)小丽被派往该院急诊科的概率是.
(2)若正好抽出她们的一位同事去往急诊科,请你利用画树状图或列表的方法,求出小丽和小王同时被派往发热门诊的概率.
解:小丽、小王和两个同事分别用A,B,C1,C2表示,根据题意画图如下:
由上可知,一共出现了12种等可能的结果,小丽和小王同时被派往发热门诊的结果有2种,
P(小丽和小王同时被派往发热门诊)==.
类型7 概率与统计的综合
14.2020年春节前夕“新型冠状病毒”爆发,疫情就是命令,防控就是使命.全国各地驰援武汉的医护工作者,践行医者仁心的使命与担当,舍小家,为大家,用自己的专业知识与血肉之躯构筑起全社会抗击疫情的钢铁长城.下面是2月9日当天全国部分省市驰援武汉医护工作者的人数统计图(不完整).
请解答下列问题:
(1)①上述省市2月9日当天驰援武汉的医护工作者的总人数为5_000人.
②请将条形统计图补充完整.
(2)请求出扇形统计图中“山东”所对应扇形的圆心角的度数.
(3)本次山东驰援武汉的医护工作者中,有5人报名去重症区,王医生和李医生就在其中,若从报名的5人中随机安排2人,求同时安排王医生和李医生去重症区的概率.
解:(1)②山东驰援武汉的医护工作者的人数为5
000-1
000-797-953-5
000×(7%+6%+6%+6%+6%)=700(人).
补充条形统计图如图.
(2)扇形统计图中“山东”所对应扇形的圆心角的度数=360°×=50.4°.
(3)画树状图为:(用A,D表示王医生和李医生)
共有20种等可能的结果,其中同时安排王医生和李医生的结果为2种,
所以P(同时安排王医生和李医生去重症区)==.
概率的综合应用
章末专题练习题
类型1 概率与数、式的综合
1.在盒子里放有分别写有整式2,π,x,x+1的四张卡片,从中随机抽取两张,把卡片上的整式分别作为分子和分母,则能组成分式的概率是(
)
A.
B.
C.
D.
类型2 概率与方程、不等式的综合
2.如果m是从-2,-1,0,1四个数中任取的一个数,那么关于x的方程=+1的根为正数的概率为____.
3.有六张正面分别标有数字-1,0,1,2,3,4的不透明卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中任取一张,则抽取的卡片上的数字为不等式组的解的概率为____.
4.有9张卡片,分别写有1~9这九个数字,将它们背面朝上洗匀后,任意抽出一张,记卡片上的数字为a,则关于x的不等式组有解的概率为____.
类型3 概率与函数的综合
5.从数-2,-1,4中随机抽取一个数记为m,再从数2,1,-4中随机抽取一个数记为n,则一次函数y=mnx中y的值随x的增大而减小的概率是____.
6.如图,把一个转盘分成四等份,依次标上数字1,2,3,4.若连续自由转动转盘两次,指针指向的数字分别记作a,b,作为点A的横、纵坐标,则点A(a,b)在函数y=2x的图象上的概率为____.
7.四个完全相同的小球上分别标有数字-2,-1,1,3,从这4个球中任意取出一个球记为a,不放回,再取出一个记为b,则能使一次函数y=2ax+b的图象必过第一、四象限的概率为____.
类型4 概率与几何的综合
8.四张质地、大小、背面完全相同的卡片上,正面分别画有下列图案,现把它们正面朝下随机摆放在桌面上,从中任意抽出一张,则抽出的卡片正面图案既是轴对称图形,又是中心对称图形的概率是(
)
A.
B.
C.
D.1
9.关于四边形ABCD有以下四个条件:①两组对边分别平行;②两条对角线互相平分;③两条对角线互相垂直;④一组邻边相等.从中任取两个条件,能得到四边形ABCD是菱形的概率是(
)
A.
B.
C.
D.
10.已知⊙O的两条直径AC,BD互相垂直,分别以AB,BC,CD,DA为直径向外作半圆得到如图所示的图形,现随机地向该图形内掷一枚小针,记针尖落在阴影区域内的概率为P1,针尖落在⊙O内的概率为P2,则=____.
类型5 概率与其他学科知识的综合
11.如图,电路图上有四个开关A,B,C,D和一个小灯泡,则任意闭合其中两个开关,小灯泡发光的概率是____.
类型6 概率的实际应用
12.某公司有甲、乙、丙三辆车去南京,它们出发的先后顺序随机.张先生和李先生乘坐该公司的车去南京出差,但有不同的需求.
请用所学概率知识解决下列问题:
(1)写出这三辆车按先后顺序出发的所有可能结果.
(2)两人中,谁乘坐到甲车的可能性大?请说明理由.
13.“一方有难,八方支援”是中华民族的传统美德,在抗击新冠病毒战役中,某省为支援武汉,派出了由1
460人组成的医疗队.其中小丽、小王和三个同事共五人直接派往一线的同一家医院,根据该医院人事安排需要先抽出一人去急诊科,再派两人到该医院的发热门诊,请你利用所学知识完成下列问题.
(1)小丽被派往该院急诊科的概率是____.
(2)若正好抽出她们的一位同事去往急诊科,请你利用画树状图或列表的方法,求出小丽和小王同时被派往发热门诊的概率.
类型7 概率与统计的综合
14.2020年春节前夕“新型冠状病毒”爆发,疫情就是命令,防控就是使命.全国各地驰援武汉的医护工作者,践行医者仁心的使命与担当,舍小家,为大家,用自己的专业知识与血肉之躯构筑起全社会抗击疫情的钢铁长城.下面是2月9日当天全国部分省市驰援武汉医护工作者的人数统计图(不完整).
请解答下列问题:
(1)①上述省市2月9日当天驰援武汉的医护工作者的总人数为____人.
②请将条形统计图补充完整.
(2)请求出扇形统计图中“山东”所对应扇形的圆心角的度数.
(3)本次山东驰援武汉的医护工作者中,有5人报名去重症区,王医生和李医生就在其中,若从报名的5人中随机安排2人,求同时安排王医生和李医生去重症区的概率.
参考答案
2021-2022学年北师大版九年级数学上册第三章
概率的综合应用
章末专题练习题
类型1 概率与数、式的综合
1.在盒子里放有分别写有整式2,π,x,x+1的四张卡片,从中随机抽取两张,把卡片上的整式分别作为分子和分母,则能组成分式的概率是(
A
)
A.
B.
C.
D.
类型2 概率与方程、不等式的综合
2.如果m是从-2,-1,0,1四个数中任取的一个数,那么关于x的方程=+1的根为正数的概率为.
3.有六张正面分别标有数字-1,0,1,2,3,4的不透明卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中任取一张,则抽取的卡片上的数字为不等式组的解的概率为.
4.有9张卡片,分别写有1~9这九个数字,将它们背面朝上洗匀后,任意抽出一张,记卡片上的数字为a,则关于x的不等式组有解的概率为.
类型3 概率与函数的综合
5.从数-2,-1,4中随机抽取一个数记为m,再从数2,1,-4中随机抽取一个数记为n,则一次函数y=mnx中y的值随x的增大而减小的概率是.
6.如图,把一个转盘分成四等份,依次标上数字1,2,3,4.若连续自由转动转盘两次,指针指向的数字分别记作a,b,作为点A的横、纵坐标,则点A(a,b)在函数y=2x的图象上的概率为.
7.四个完全相同的小球上分别标有数字-2,-1,1,3,从这4个球中任意取出一个球记为a,不放回,再取出一个记为b,则能使一次函数y=2ax+b的图象必过第一、四象限的概率为.
类型4 概率与几何的综合
8.四张质地、大小、背面完全相同的卡片上,正面分别画有下列图案,现把它们正面朝下随机摆放在桌面上,从中任意抽出一张,则抽出的卡片正面图案既是轴对称图形,又是中心对称图形的概率是(
B
)
A.
B.
C.
D.1
9.关于四边形ABCD有以下四个条件:①两组对边分别平行;②两条对角线互相平分;③两条对角线互相垂直;④一组邻边相等.从中任取两个条件,能得到四边形ABCD是菱形的概率是(
A
)
A.
B.
C.
D.
10.已知⊙O的两条直径AC,BD互相垂直,分别以AB,BC,CD,DA为直径向外作半圆得到如图所示的图形,现随机地向该图形内掷一枚小针,记针尖落在阴影区域内的概率为P1,针尖落在⊙O内的概率为P2,则=.
类型5 概率与其他学科知识的综合
11.如图,电路图上有四个开关A,B,C,D和一个小灯泡,则任意闭合其中两个开关,小灯泡发光的概率是.
类型6 概率的实际应用
12.某公司有甲、乙、丙三辆车去南京,它们出发的先后顺序随机.张先生和李先生乘坐该公司的车去南京出差,但有不同的需求.
请用所学概率知识解决下列问题:
(1)写出这三辆车按先后顺序出发的所有可能结果.
(2)两人中,谁乘坐到甲车的可能性大?请说明理由.
解:(1)这三辆车按先后顺序出发的所有可能结果:
甲、乙、丙;甲、丙、乙;乙、甲、丙;乙、丙、甲;丙、甲、乙;丙、乙、甲;共6种.
(2)两人坐到甲车的可能性一样.理由:
由(1)可知张先生坐到甲车有两种可能:乙、丙、甲和丙、乙、甲,则张先生坐到甲车的概率是=.
由(1)可知李先生坐到甲车有两种可能:甲、乙、丙和甲、丙、乙,则李先生坐到甲车的概率是=.
所以两人坐到甲车的可能性一样.
13.“一方有难,八方支援”是中华民族的传统美德,在抗击新冠病毒战役中,某省为支援武汉,派出了由1
460人组成的医疗队.其中小丽、小王和三个同事共五人直接派往一线的同一家医院,根据该医院人事安排需要先抽出一人去急诊科,再派两人到该医院的发热门诊,请你利用所学知识完成下列问题.
(1)小丽被派往该院急诊科的概率是.
(2)若正好抽出她们的一位同事去往急诊科,请你利用画树状图或列表的方法,求出小丽和小王同时被派往发热门诊的概率.
解:小丽、小王和两个同事分别用A,B,C1,C2表示,根据题意画图如下:
由上可知,一共出现了12种等可能的结果,小丽和小王同时被派往发热门诊的结果有2种,
P(小丽和小王同时被派往发热门诊)==.
类型7 概率与统计的综合
14.2020年春节前夕“新型冠状病毒”爆发,疫情就是命令,防控就是使命.全国各地驰援武汉的医护工作者,践行医者仁心的使命与担当,舍小家,为大家,用自己的专业知识与血肉之躯构筑起全社会抗击疫情的钢铁长城.下面是2月9日当天全国部分省市驰援武汉医护工作者的人数统计图(不完整).
请解答下列问题:
(1)①上述省市2月9日当天驰援武汉的医护工作者的总人数为5_000人.
②请将条形统计图补充完整.
(2)请求出扇形统计图中“山东”所对应扇形的圆心角的度数.
(3)本次山东驰援武汉的医护工作者中,有5人报名去重症区,王医生和李医生就在其中,若从报名的5人中随机安排2人,求同时安排王医生和李医生去重症区的概率.
解:(1)②山东驰援武汉的医护工作者的人数为5
000-1
000-797-953-5
000×(7%+6%+6%+6%+6%)=700(人).
补充条形统计图如图.
(2)扇形统计图中“山东”所对应扇形的圆心角的度数=360°×=50.4°.
(3)画树状图为:(用A,D表示王医生和李医生)
共有20种等可能的结果,其中同时安排王医生和李医生的结果为2种,
所以P(同时安排王医生和李医生去重症区)==.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
