2021-2022学年北师大版九年级数学上册1.2.3 矩形的性质与判定的运用同步练习题(Word版,含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学上册1.2.3 矩形的性质与判定的运用同步练习题(Word版,含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 113.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-22 23:42:08 | ||
图片预览



文档简介
1.2.3矩形的性质与判定的运用
同步练习题
2021-2022学年北师大版九年级数学上册
A组(基础题)
一、填空题
1.如图,AB∥CD,∠A=∠B=90°,AB=3
cm,BC=2
cm,则AB与CD之间的距离为_____cm.
2.如图,在矩形ABCD中,AB=3,对角线AC,BD相交于点O,AE垂直平分OB于点E,则AD的长为_____.
3.如图,在矩形ABCD中,AB=3,AD=4,过点A作AG⊥BD于点G,则BG=_____.
4.如图,在矩形ABCD中,BD是对角线,延长AD到E,使DE=BD,连接BE.若∠EBC=27°,则∠ABD=_____度.
二、选择题
5.如图,在四边形ABCD中,AB=DC,AD=BC,连接AC,BD,AC与BD交于点O.若AO=BO,AD=3,AB=2,则四边形ABCD的面积为(
)
A.4
B.5
C.6
D.7
6.如图,将矩形纸片ABCD沿直线EF折叠,使点C落在AD边的中点C′处,点B落在点B′处,其中AB=9,BC=6,则FC′的长为(
)
A.
B.4
C.4.5
D.5
7.如图,在矩形钟面示意图中,时钟的中心在矩形对角线的交点上,矩形的宽为40
cm,钟面数字2在矩形的顶点处,则矩形的长为____cm(
)
A.80
B.60
C.50
D.40
8.如图,矩形ABCD中,点E是BC上一动点,连接AE,DE,以AE,DE为边作?AEDF,当点E从点B运动到点C的过程中,?AEDF的面积(
)
A.先变小后变大
B.先变大后变小
C.保持不变
D.一直变大
三、解答题
9.如图,菱形ABCD的对角线相交于点O,DE∥AC,CE∥DB,CE,DE相交于点E.
(1)求证:四边形DOCE是矩形.
(2)若四边形DOCE的面积是3,AC+BD=10,求AB的长.
B组(中档题)
四、填空题
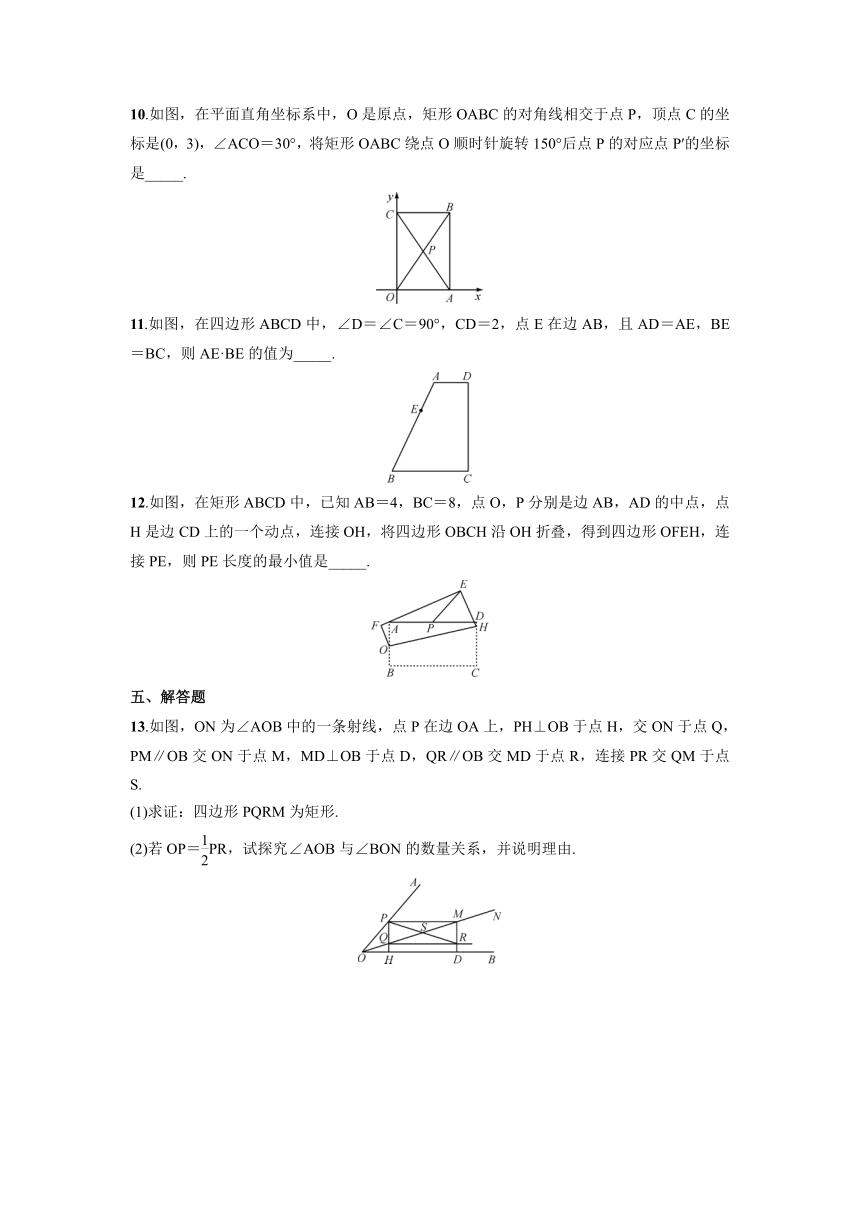
10.如图,在平面直角坐标系中,O是原点,矩形OABC的对角线相交于点P,顶点C的坐标是(0,3),∠ACO=30°,将矩形OABC绕点O顺时针旋转150°后点P的对应点P′的坐标是_____.
11.如图,在四边形ABCD中,∠D=∠C=90°,CD=2,点E在边AB,且AD=AE,BE=BC,则AE·BE的值为_____.
12.如图,在矩形ABCD中,已知AB=4,BC=8,点O,P分别是边AB,AD的中点,点H是边CD上的一个动点,连接OH,将四边形OBCH沿OH折叠,得到四边形OFEH,连接PE,则PE长度的最小值是_____.
五、解答题
13.如图,ON为∠AOB中的一条射线,点P在边OA上,PH⊥OB于点H,交ON于点Q,PM∥OB交ON于点M,MD⊥OB于点D,QR∥OB交MD于点R,连接PR交QM于点S.
(1)求证:四边形PQRM为矩形.
(2)若OP=PR,试探究∠AOB与∠BON的数量关系,并说明理由.
C组(综合题)
14.如图1,一张菱形纸片EHGF,点A,D,C,B分别是EF,EH,HG,GF边上的点,连接AD,DC,CB,AB,DB,且AD=,AB=;如图2,若将△FAB,△AED,△DHC,△CGB分别沿AB,AD,DC,CB对折,点E,F都落在DB上的点P处,点H,G都落在DB上的点Q处.
(1)求证:四边形ADCB是矩形.
(2)求菱形纸片EHGF的面积和边长.
参考答案
1.2.3矩形的性质与判定的运用
同步练习题
2021-2022学年北师大版九年级数学上册
A组(基础题)
一、填空题
1.如图,AB∥CD,∠A=∠B=90°,AB=3
cm,BC=2
cm,则AB与CD之间的距离为2cm.
2.如图,在矩形ABCD中,AB=3,对角线AC,BD相交于点O,AE垂直平分OB于点E,则AD的长为3.
3.如图,在矩形ABCD中,AB=3,AD=4,过点A作AG⊥BD于点G,则BG=.
4.如图,在矩形ABCD中,BD是对角线,延长AD到E,使DE=BD,连接BE.若∠EBC=27°,则∠ABD=36度.
二、选择题
5.如图,在四边形ABCD中,AB=DC,AD=BC,连接AC,BD,AC与BD交于点O.若AO=BO,AD=3,AB=2,则四边形ABCD的面积为(
C
)
A.4
B.5
C.6
D.7
6.如图,将矩形纸片ABCD沿直线EF折叠,使点C落在AD边的中点C′处,点B落在点B′处,其中AB=9,BC=6,则FC′的长为(
D
)
A.
B.4
C.4.5
D.5
7.如图,在矩形钟面示意图中,时钟的中心在矩形对角线的交点上,矩形的宽为40
cm,钟面数字2在矩形的顶点处,则矩形的长为____cm(
D
)
A.80
B.60
C.50
D.40
8.如图,矩形ABCD中,点E是BC上一动点,连接AE,DE,以AE,DE为边作?AEDF,当点E从点B运动到点C的过程中,?AEDF的面积(
C
)
A.先变小后变大
B.先变大后变小
C.保持不变
D.一直变大
三、解答题
9.如图,菱形ABCD的对角线相交于点O,DE∥AC,CE∥DB,CE,DE相交于点E.
(1)求证:四边形DOCE是矩形.
(2)若四边形DOCE的面积是3,AC+BD=10,求AB的长.
(1)证明:∵DE∥AC,CE∥DB,
∴四边形DOCE是平行四边形.
∵四边形ABCD是菱形,
∴AC⊥BD.
∴∠COD=90°.
∴四边形DOCE是矩形.
(2)设OD=x,OC=y,
∵四边形ABCD是菱形,
∴OA=OC,OB=OD,AC⊥BD.
∵AC+BD=10,四边形DOCE的面积是3,
∴x+y=5,xy=3.
∴x2+y2=(x+y)2-2xy=52-2×3=19.
∴AB===.
B组(中档题)
四、填空题
10.如图,在平面直角坐标系中,O是原点,矩形OABC的对角线相交于点P,顶点C的坐标是(0,3),∠ACO=30°,将矩形OABC绕点O顺时针旋转150°后点P的对应点P′的坐标是(0,-).
11.如图,在四边形ABCD中,∠D=∠C=90°,CD=2,点E在边AB,且AD=AE,BE=BC,则AE·BE的值为1.
12.如图,在矩形ABCD中,已知AB=4,BC=8,点O,P分别是边AB,AD的中点,点H是边CD上的一个动点,连接OH,将四边形OBCH沿OH折叠,得到四边形OFEH,连接PE,则PE长度的最小值是2-2.
五、解答题
13.如图,ON为∠AOB中的一条射线,点P在边OA上,PH⊥OB于点H,交ON于点Q,PM∥OB交ON于点M,MD⊥OB于点D,QR∥OB交MD于点R,连接PR交QM于点S.
(1)求证:四边形PQRM为矩形.
(2)若OP=PR,试探究∠AOB与∠BON的数量关系,并说明理由.
解:(1)证明:∵PH⊥OB,MD⊥OB,
∴PH∥MD.
∵PM∥OB,QR∥OB,
∴PM∥QR.
∴四边形PQRM是平行四边形.
∵PH⊥OB,∴∠PHO=90°.
∵PM∥OB,
∴∠MPQ=∠PHO=90°.
∴四边形PQRM为矩形.
(2)∠AOB=3∠BON.理由如下:
∵四边形PQRM为矩形,
∴PS=SR=SQ=PR.
∴∠SQR=∠SRQ.
又∵OP=PR,
∴OP=PS.
∴∠POS=∠PSO.
∵QR∥OB,
∴∠SQR=∠BON.
在△SQR中,∠PSO=∠SQR+∠SRQ=2∠SQR=2∠BON,
∴∠POS=2∠BON.
∴∠AOB=∠POS+∠BON=2∠BON+∠BON=3∠BON,即∠AOB=3∠BON.
C组(综合题)
14.如图1,一张菱形纸片EHGF,点A,D,C,B分别是EF,EH,HG,GF边上的点,连接AD,DC,CB,AB,DB,且AD=,AB=;如图2,若将△FAB,△AED,△DHC,△CGB分别沿AB,AD,DC,CB对折,点E,F都落在DB上的点P处,点H,G都落在DB上的点Q处.
(1)求证:四边形ADCB是矩形.
(2)求菱形纸片EHGF的面积和边长.
解:(1)证明:由对折可知∠FAB=∠PAB,∠EAD=∠PAD,
∴2(∠PAB+∠PAD)=180°,
即∠BAD=∠PAB+∠PAD=90°.
同理:∠ADC=∠ABC=90°.
∴四边形ADCB是矩形.
(2)由对折可知:△AFB≌△APB,△AED≌△APD,△CHD≌△CQD,△CGB≌△CQB.
∴S菱形EHGF=2S矩形ADCB=2××=6.
又∵AE=AP=AF,
∴A为EF的中点,
同理:C为GH的中点,即AF=CG,且AF∥CG.
连接AC,
∴四边形ACGF为平行四边形.
∴FG=AC=BD.
∴FG=BD==3.
同步练习题
2021-2022学年北师大版九年级数学上册
A组(基础题)
一、填空题
1.如图,AB∥CD,∠A=∠B=90°,AB=3
cm,BC=2
cm,则AB与CD之间的距离为_____cm.
2.如图,在矩形ABCD中,AB=3,对角线AC,BD相交于点O,AE垂直平分OB于点E,则AD的长为_____.
3.如图,在矩形ABCD中,AB=3,AD=4,过点A作AG⊥BD于点G,则BG=_____.
4.如图,在矩形ABCD中,BD是对角线,延长AD到E,使DE=BD,连接BE.若∠EBC=27°,则∠ABD=_____度.
二、选择题
5.如图,在四边形ABCD中,AB=DC,AD=BC,连接AC,BD,AC与BD交于点O.若AO=BO,AD=3,AB=2,则四边形ABCD的面积为(
)
A.4
B.5
C.6
D.7
6.如图,将矩形纸片ABCD沿直线EF折叠,使点C落在AD边的中点C′处,点B落在点B′处,其中AB=9,BC=6,则FC′的长为(
)
A.
B.4
C.4.5
D.5
7.如图,在矩形钟面示意图中,时钟的中心在矩形对角线的交点上,矩形的宽为40
cm,钟面数字2在矩形的顶点处,则矩形的长为____cm(
)
A.80
B.60
C.50
D.40
8.如图,矩形ABCD中,点E是BC上一动点,连接AE,DE,以AE,DE为边作?AEDF,当点E从点B运动到点C的过程中,?AEDF的面积(
)
A.先变小后变大
B.先变大后变小
C.保持不变
D.一直变大
三、解答题
9.如图,菱形ABCD的对角线相交于点O,DE∥AC,CE∥DB,CE,DE相交于点E.
(1)求证:四边形DOCE是矩形.
(2)若四边形DOCE的面积是3,AC+BD=10,求AB的长.
B组(中档题)
四、填空题
10.如图,在平面直角坐标系中,O是原点,矩形OABC的对角线相交于点P,顶点C的坐标是(0,3),∠ACO=30°,将矩形OABC绕点O顺时针旋转150°后点P的对应点P′的坐标是_____.
11.如图,在四边形ABCD中,∠D=∠C=90°,CD=2,点E在边AB,且AD=AE,BE=BC,则AE·BE的值为_____.
12.如图,在矩形ABCD中,已知AB=4,BC=8,点O,P分别是边AB,AD的中点,点H是边CD上的一个动点,连接OH,将四边形OBCH沿OH折叠,得到四边形OFEH,连接PE,则PE长度的最小值是_____.
五、解答题
13.如图,ON为∠AOB中的一条射线,点P在边OA上,PH⊥OB于点H,交ON于点Q,PM∥OB交ON于点M,MD⊥OB于点D,QR∥OB交MD于点R,连接PR交QM于点S.
(1)求证:四边形PQRM为矩形.
(2)若OP=PR,试探究∠AOB与∠BON的数量关系,并说明理由.
C组(综合题)
14.如图1,一张菱形纸片EHGF,点A,D,C,B分别是EF,EH,HG,GF边上的点,连接AD,DC,CB,AB,DB,且AD=,AB=;如图2,若将△FAB,△AED,△DHC,△CGB分别沿AB,AD,DC,CB对折,点E,F都落在DB上的点P处,点H,G都落在DB上的点Q处.
(1)求证:四边形ADCB是矩形.
(2)求菱形纸片EHGF的面积和边长.
参考答案
1.2.3矩形的性质与判定的运用
同步练习题
2021-2022学年北师大版九年级数学上册
A组(基础题)
一、填空题
1.如图,AB∥CD,∠A=∠B=90°,AB=3
cm,BC=2
cm,则AB与CD之间的距离为2cm.
2.如图,在矩形ABCD中,AB=3,对角线AC,BD相交于点O,AE垂直平分OB于点E,则AD的长为3.
3.如图,在矩形ABCD中,AB=3,AD=4,过点A作AG⊥BD于点G,则BG=.
4.如图,在矩形ABCD中,BD是对角线,延长AD到E,使DE=BD,连接BE.若∠EBC=27°,则∠ABD=36度.
二、选择题
5.如图,在四边形ABCD中,AB=DC,AD=BC,连接AC,BD,AC与BD交于点O.若AO=BO,AD=3,AB=2,则四边形ABCD的面积为(
C
)
A.4
B.5
C.6
D.7
6.如图,将矩形纸片ABCD沿直线EF折叠,使点C落在AD边的中点C′处,点B落在点B′处,其中AB=9,BC=6,则FC′的长为(
D
)
A.
B.4
C.4.5
D.5
7.如图,在矩形钟面示意图中,时钟的中心在矩形对角线的交点上,矩形的宽为40
cm,钟面数字2在矩形的顶点处,则矩形的长为____cm(
D
)
A.80
B.60
C.50
D.40
8.如图,矩形ABCD中,点E是BC上一动点,连接AE,DE,以AE,DE为边作?AEDF,当点E从点B运动到点C的过程中,?AEDF的面积(
C
)
A.先变小后变大
B.先变大后变小
C.保持不变
D.一直变大
三、解答题
9.如图,菱形ABCD的对角线相交于点O,DE∥AC,CE∥DB,CE,DE相交于点E.
(1)求证:四边形DOCE是矩形.
(2)若四边形DOCE的面积是3,AC+BD=10,求AB的长.
(1)证明:∵DE∥AC,CE∥DB,
∴四边形DOCE是平行四边形.
∵四边形ABCD是菱形,
∴AC⊥BD.
∴∠COD=90°.
∴四边形DOCE是矩形.
(2)设OD=x,OC=y,
∵四边形ABCD是菱形,
∴OA=OC,OB=OD,AC⊥BD.
∵AC+BD=10,四边形DOCE的面积是3,
∴x+y=5,xy=3.
∴x2+y2=(x+y)2-2xy=52-2×3=19.
∴AB===.
B组(中档题)
四、填空题
10.如图,在平面直角坐标系中,O是原点,矩形OABC的对角线相交于点P,顶点C的坐标是(0,3),∠ACO=30°,将矩形OABC绕点O顺时针旋转150°后点P的对应点P′的坐标是(0,-).
11.如图,在四边形ABCD中,∠D=∠C=90°,CD=2,点E在边AB,且AD=AE,BE=BC,则AE·BE的值为1.
12.如图,在矩形ABCD中,已知AB=4,BC=8,点O,P分别是边AB,AD的中点,点H是边CD上的一个动点,连接OH,将四边形OBCH沿OH折叠,得到四边形OFEH,连接PE,则PE长度的最小值是2-2.
五、解答题
13.如图,ON为∠AOB中的一条射线,点P在边OA上,PH⊥OB于点H,交ON于点Q,PM∥OB交ON于点M,MD⊥OB于点D,QR∥OB交MD于点R,连接PR交QM于点S.
(1)求证:四边形PQRM为矩形.
(2)若OP=PR,试探究∠AOB与∠BON的数量关系,并说明理由.
解:(1)证明:∵PH⊥OB,MD⊥OB,
∴PH∥MD.
∵PM∥OB,QR∥OB,
∴PM∥QR.
∴四边形PQRM是平行四边形.
∵PH⊥OB,∴∠PHO=90°.
∵PM∥OB,
∴∠MPQ=∠PHO=90°.
∴四边形PQRM为矩形.
(2)∠AOB=3∠BON.理由如下:
∵四边形PQRM为矩形,
∴PS=SR=SQ=PR.
∴∠SQR=∠SRQ.
又∵OP=PR,
∴OP=PS.
∴∠POS=∠PSO.
∵QR∥OB,
∴∠SQR=∠BON.
在△SQR中,∠PSO=∠SQR+∠SRQ=2∠SQR=2∠BON,
∴∠POS=2∠BON.
∴∠AOB=∠POS+∠BON=2∠BON+∠BON=3∠BON,即∠AOB=3∠BON.
C组(综合题)
14.如图1,一张菱形纸片EHGF,点A,D,C,B分别是EF,EH,HG,GF边上的点,连接AD,DC,CB,AB,DB,且AD=,AB=;如图2,若将△FAB,△AED,△DHC,△CGB分别沿AB,AD,DC,CB对折,点E,F都落在DB上的点P处,点H,G都落在DB上的点Q处.
(1)求证:四边形ADCB是矩形.
(2)求菱形纸片EHGF的面积和边长.
解:(1)证明:由对折可知∠FAB=∠PAB,∠EAD=∠PAD,
∴2(∠PAB+∠PAD)=180°,
即∠BAD=∠PAB+∠PAD=90°.
同理:∠ADC=∠ABC=90°.
∴四边形ADCB是矩形.
(2)由对折可知:△AFB≌△APB,△AED≌△APD,△CHD≌△CQD,△CGB≌△CQB.
∴S菱形EHGF=2S矩形ADCB=2××=6.
又∵AE=AP=AF,
∴A为EF的中点,
同理:C为GH的中点,即AF=CG,且AF∥CG.
连接AC,
∴四边形ACGF为平行四边形.
∴FG=AC=BD.
∴FG=BD==3.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
