2021-2022学年北师大版九年级数学上册1.3.2正方形的判定同步练习题(Word版,含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学上册1.3.2正方形的判定同步练习题(Word版,含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 129.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-22 23:55:59 | ||
图片预览


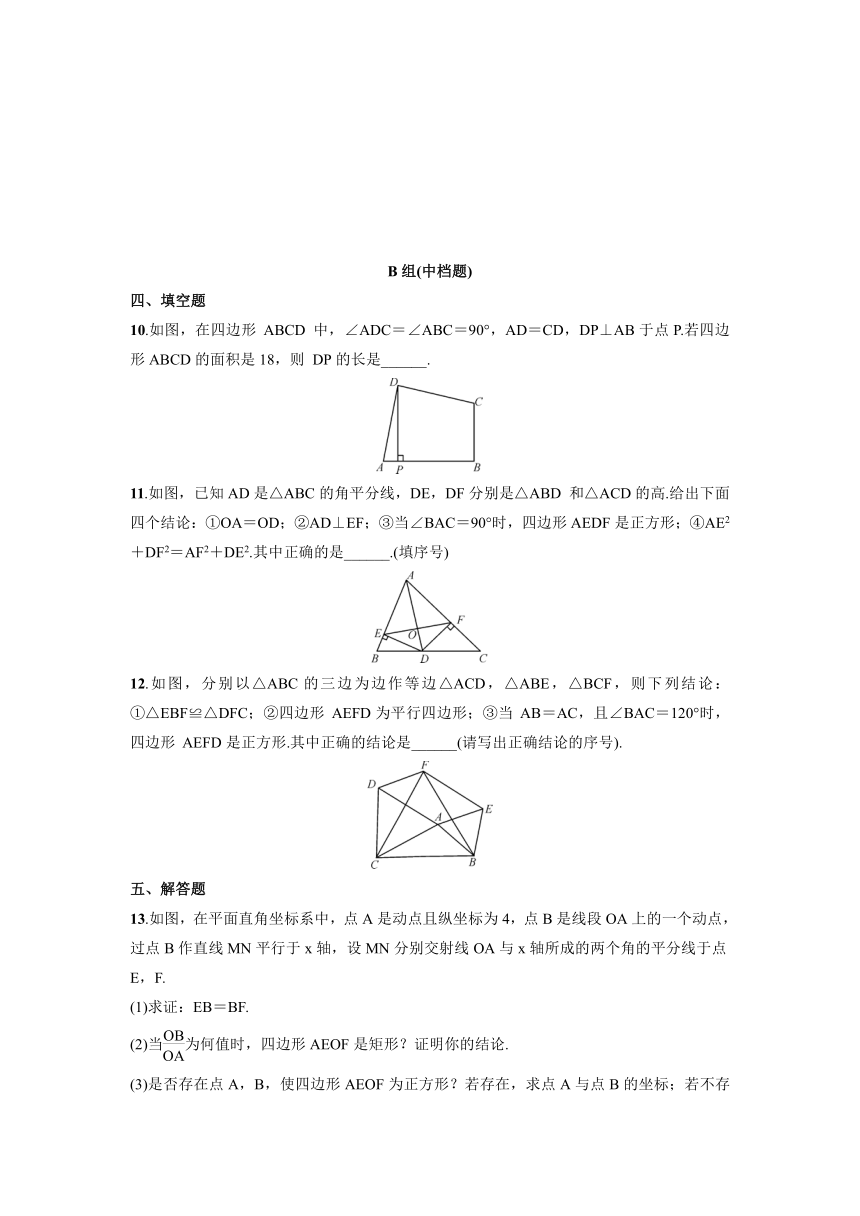

文档简介
1.3.2正方形的判定
同步练习题
2021-2022学年北师大版九年级数学上册
A组(基础题)
一、填空题
1.(1)一个四边形满足__________________时,是正方形.
(2)一个平行四边形满足__________________时,是正方形.
(3)一个矩形满足__________________时,是正方形.
(4)一个菱形满足__________________时,是正方形.
2.如图,将一张矩形纸片对折两次(两条折痕互相垂直),然后剪下一个角后,打开这个角,如果要剪出一个正方形,那么剪口线与折痕成______角.
3.如图,在四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA
的中点.若使四边形EFGH为正方形,则四边形ABCD的对角线应具有的性质是______.
二、选择题
4.如图,在菱形
ABCD中,对角线AC,BD交于点O,添加下列一个条件,能使菱形ABCD成为正方形的是(
)
A.BD=AB
B.AC=AD
C.∠ABC=90°
D.OD=AC
5.下列是关于某个四边形的三个结论:①它的对角线相等;②它是一个正方形;③它是一个矩形.下列推理过程正确的是(
)
A.由②推出③,由③推出①
B.由①推出②,由②推出③
C.由③推出①,由①推出②
D.由①推出③,由③推出②
6.如图所示,两个含30°角的完全相同的三角板ABC和三角板DEF沿直线l滑动,下列说法错误的是(
)
A.四边形ACDF是平行四边形
B.当点E为BC中点时,四边形ACDF是矩形
C.当点B与点E重合时,四边形ACDF是菱形
D.四边形ACDF不可能是正方形
7.在一次数学课上,张老师出示了一个题目:“如图,?ABCD的对角线相交于点O,过点O作EF⊥BD分别交AB,CD于点F,E,连接
DF,BE.请根据上述条件,写出一个正确结论.”有四位同学分别写出的结论如下:
小青:OE=OF;小何:四边形
DFBE是正方形;
小夏:S四边形AFED=S四边形FECB
;小雨:∠ACE=∠CAF.
这四位同学写出的结论中不正确的是(
)
A.小青
B.小何
C.小夏
D.小雨
三、解答题
8.如图,等边△AEF的顶点E,F在矩形ABCD的边BC,CD上,且∠CEF=45°.求证:矩形ABCD是正方形.
9.如图,在四边形ABFC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE.
(1)试判断四边形
BECF是什么四边形,并说明理由.
(2)当∠A的大小满足什么条件时,四边形BECF是正方形?请回答并证明你的结论.
B组(中档题)
四、填空题
10.如图,在四边形
ABCD
中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于点P.若四边形ABCD的面积是18,则
DP的长是______.
11.如图,已知AD是△ABC的角平分线,DE,DF分别是△ABD
和△ACD的高.给出下面四个结论:①OA=OD;②AD⊥EF;③当∠BAC=90°时,四边形AEDF是正方形;④AE2+DF2=AF2+DE2.其中正确的是______.(填序号)
12.如图,分别以△ABC的三边为边作等边△ACD,△ABE,△BCF,则下列结论:①△EBF≌△DFC;②四边形
AEFD为平行四边形;③当
AB=AC,且∠BAC=120°时,四边形
AEFD是正方形.其中正确的结论是______(请写出正确结论的序号).
五、解答题
13.如图,在平面直角坐标系中,点A是动点且纵坐标为4,点B是线段OA上的一个动点,过点B作直线MN平行于x轴,设MN分别交射线OA与x轴所成的两个角的平分线于点E,F.
(1)求证:EB=BF.
(2)当为何值时,四边形AEOF是矩形?证明你的结论.
(3)是否存在点A,B,使四边形AEOF为正方形?若存在,求点A与点B的坐标;若不存在,说明理由.
C组(综合题)
14.如图,四边形
ABCD为正方形,E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE,EF为邻边作矩形
DEFG,连接CG.
(1)求证:矩形
DEFG是正方形.
(2)若AB=2,CE=,求CG的长度.
(3)当线段DE与正方形ABCD
的某条边的夹角是30°时,直接写出∠EFC的度数.
参考答案
1.3.2正方形的判定
同步练习题
2021-2022学年北师大版九年级数学上册
A组(基础题)
一、填空题
1.(1)一个四边形满足对角线互相垂直平分且相等(答案不唯一)时,是正方形.
(2)一个平行四边形满足对角线互相垂直且相等(答案不唯一)时,是正方形.
(3)一个矩形满足对角线互相垂直(答案不唯一)时,是正方形.
(4)一个菱形满足对角线相等(答案不唯一)时,是正方形.
2.如图,将一张矩形纸片对折两次(两条折痕互相垂直),然后剪下一个角后,打开这个角,如果要剪出一个正方形,那么剪口线与折痕成45°角.
3.如图,在四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA
的中点.若使四边形EFGH为正方形,则四边形ABCD的对角线应具有的性质是垂直且相等.
二、选择题
4.如图,在菱形
ABCD中,对角线AC,BD交于点O,添加下列一个条件,能使菱形ABCD成为正方形的是(
C
)
A.BD=AB
B.AC=AD
C.∠ABC=90°
D.OD=AC
5.下列是关于某个四边形的三个结论:①它的对角线相等;②它是一个正方形;③它是一个矩形.下列推理过程正确的是(
A
)
A.由②推出③,由③推出①
B.由①推出②,由②推出③
C.由③推出①,由①推出②
D.由①推出③,由③推出②
6.如图所示,两个含30°角的完全相同的三角板ABC和三角板DEF沿直线l滑动,下列说法错误的是(
B
)
A.四边形ACDF是平行四边形
B.当点E为BC中点时,四边形ACDF是矩形
C.当点B与点E重合时,四边形ACDF是菱形
D.四边形ACDF不可能是正方形
7.在一次数学课上,张老师出示了一个题目:“如图,?ABCD的对角线相交于点O,过点O作EF⊥BD分别交AB,CD于点F,E,连接
DF,BE.请根据上述条件,写出一个正确结论.”有四位同学分别写出的结论如下:
小青:OE=OF;小何:四边形
DFBE是正方形;
小夏:S四边形AFED=S四边形FECB
;小雨:∠ACE=∠CAF.
这四位同学写出的结论中不正确的是(
B
)
A.小青
B.小何
C.小夏
D.小雨
三、解答题
8.如图,等边△AEF的顶点E,F在矩形ABCD的边BC,CD上,且∠CEF=45°.求证:矩形ABCD是正方形.
证明:∵四边形ABCD是矩形,
∴∠B=∠D=∠C=90°.
∵△AEF是等边三角形,
∴AE=AF,∠AEF=∠AFE=60°.
∵∠CEF=45°,∴∠CFE=∠CEF=45°.
∴∠AFD=∠AEB=180°-45°-60°=75°.
∴△AEB≌△AFD(AAS).
∴AB=AD.
∴矩形ABCD是正方形.
9.如图,在四边形ABFC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE.
(1)试判断四边形
BECF是什么四边形,并说明理由.
(2)当∠A的大小满足什么条件时,四边形BECF是正方形?请回答并证明你的结论.
解:(1)四边形BECF是菱形.理由如下:
∵EF垂直平分BC,
∴BF=FC,BE=EC.
∴∠EBC=∠ECB.
∵∠ACB=90°,
∴∠EBC+∠A=90°,∠ECB+∠ACE=90°.
∴∠A=∠ACE.∴EC=AE.
∴BE=AE.
又∵CF=AE.
∴BE=EC=CF=BF.
∴四边形BECF是菱形.
(2)当∠A=45°时,菱形BECF是正方形.
证明如下:∵∠ACE=∠A=45°,∴∠CEA=90°.
∵四边形BECF是菱形,
∴四边形BECF是正方形.
故当∠A=45°时,四边形BECF是正方形.
B组(中档题)
四、填空题
10.如图,在四边形
ABCD
中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于点P.若四边形ABCD的面积是18,则
DP的长是3.
11.如图,已知AD是△ABC的角平分线,DE,DF分别是△ABD
和△ACD的高.给出下面四个结论:①OA=OD;②AD⊥EF;③当∠BAC=90°时,四边形AEDF是正方形;④AE2+DF2=AF2+DE2.其中正确的是②③④.(填序号)
12.如图,分别以△ABC的三边为边作等边△ACD,△ABE,△BCF,则下列结论:①△EBF≌△DFC;②四边形
AEFD为平行四边形;③当
AB=AC,且∠BAC=120°时,四边形
AEFD是正方形.其中正确的结论是①②(请写出正确结论的序号).
五、解答题
13.如图,在平面直角坐标系中,点A是动点且纵坐标为4,点B是线段OA上的一个动点,过点B作直线MN平行于x轴,设MN分别交射线OA与x轴所成的两个角的平分线于点E,F.
(1)求证:EB=BF.
(2)当为何值时,四边形AEOF是矩形?证明你的结论.
(3)是否存在点A,B,使四边形AEOF为正方形?若存在,求点A与点B的坐标;若不存在,说明理由.
解:(1)证明:∵OF是∠AOx的平分线,∴∠AOF=∠FOx,
∵MN∥x轴,∴∠MFO=∠FOx,
∴∠AOF=∠MFO.∴BO=BF.
同理:BO=BE,
∴EB=BF.
(2)当=,四边形AEOF是矩形.
证明:∵=,∴OB=AB.
又∵BE=BF,
∴四边形AEOF是平行四边形.
∵OE,OF是角平分线,∴∠EOF=90°,
∴四边形AEOF是矩形.
(3)存在点A,B使四边形AEOF为正方形,
∵MN∥x轴,
∴当A点在y轴时,即A点坐标为(0,4)时,有OA⊥EF,此时,取OA的中点B(0,2),由(2)知四边形AEOF是矩形.
∴四边形AEOF为正方形.
∴存在A(0,4),B(0,2),使四边形AEOF为正方形.
C组(综合题)
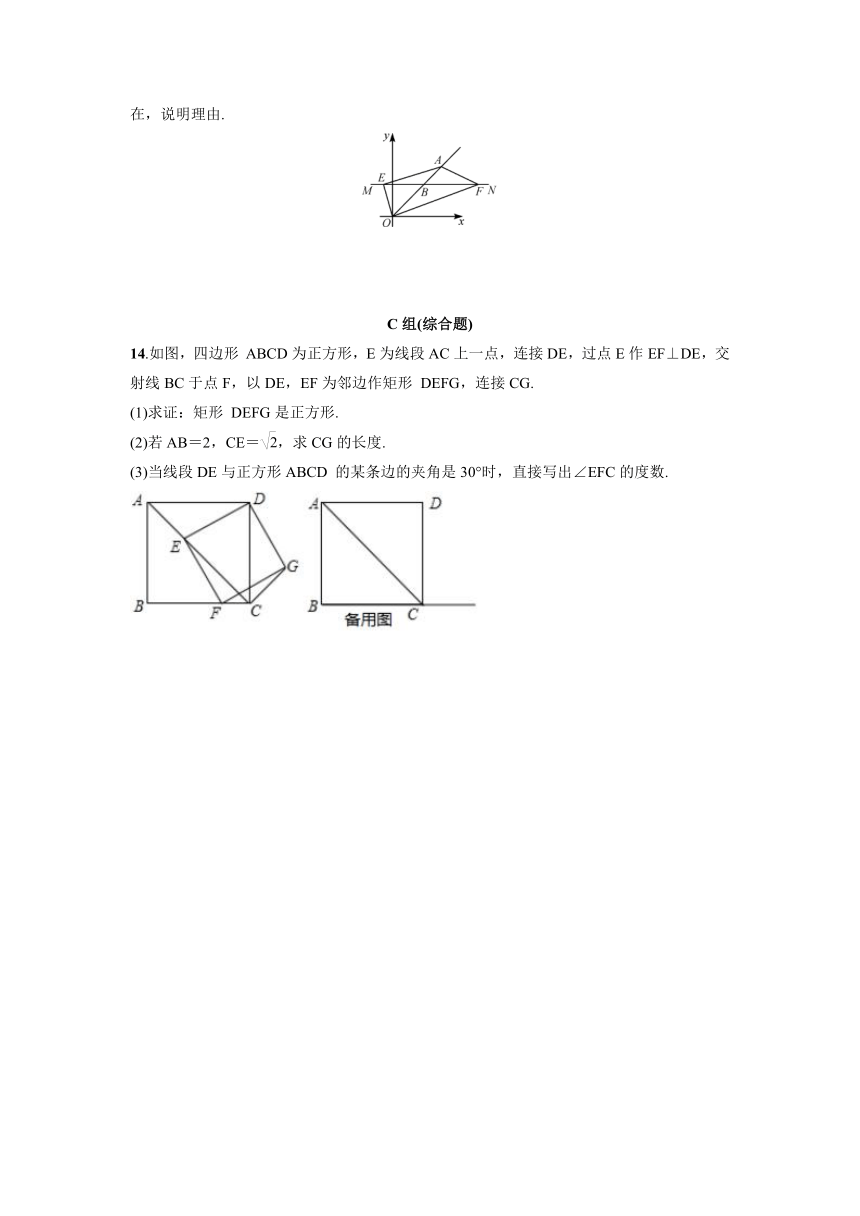
14.如图,四边形
ABCD为正方形,E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE,EF为邻边作矩形
DEFG,连接CG.
(1)求证:矩形
DEFG是正方形.
(2)若AB=2,CE=,求CG的长度.
(3)当线段DE与正方形ABCD
的某条边的夹角是30°时,直接写出∠EFC的度数.
解:(1)证明:过点E作EP⊥CD于点P,EQ⊥BC于点Q.
∴∠EQF=∠EPD.
∵四边形ABCD是正方形,
∴∠DCA=∠BCA.
∴EQ=EP,∠QEC=∠PEC=45°.
∴∠QEF+∠FEC=45°.
∵四边形DEFG是矩形,
∴∠DEF=90°.
∴∠PED+∠FEC=45°.
∴∠QEF=∠PED.
∴△EQF≌△EPD(ASA).
∴EF=ED.
∴矩形DEFG是正方形.
(2)在Rt△ABC中,AC==AB=2.
∵CE=,∴AE=CE=AC.
∴点F与点C重合,此时△DCG是等腰直角三角形,易知CG=.
(3)①当DE与AD的夹角为30°时,∠EFC=120°;
②当DE与
DC的夹角为30°时,∠EFC=30°.
综上所述,∠EFC=120°或30°.
同步练习题
2021-2022学年北师大版九年级数学上册
A组(基础题)
一、填空题
1.(1)一个四边形满足__________________时,是正方形.
(2)一个平行四边形满足__________________时,是正方形.
(3)一个矩形满足__________________时,是正方形.
(4)一个菱形满足__________________时,是正方形.
2.如图,将一张矩形纸片对折两次(两条折痕互相垂直),然后剪下一个角后,打开这个角,如果要剪出一个正方形,那么剪口线与折痕成______角.
3.如图,在四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA
的中点.若使四边形EFGH为正方形,则四边形ABCD的对角线应具有的性质是______.
二、选择题
4.如图,在菱形
ABCD中,对角线AC,BD交于点O,添加下列一个条件,能使菱形ABCD成为正方形的是(
)
A.BD=AB
B.AC=AD
C.∠ABC=90°
D.OD=AC
5.下列是关于某个四边形的三个结论:①它的对角线相等;②它是一个正方形;③它是一个矩形.下列推理过程正确的是(
)
A.由②推出③,由③推出①
B.由①推出②,由②推出③
C.由③推出①,由①推出②
D.由①推出③,由③推出②
6.如图所示,两个含30°角的完全相同的三角板ABC和三角板DEF沿直线l滑动,下列说法错误的是(
)
A.四边形ACDF是平行四边形
B.当点E为BC中点时,四边形ACDF是矩形
C.当点B与点E重合时,四边形ACDF是菱形
D.四边形ACDF不可能是正方形
7.在一次数学课上,张老师出示了一个题目:“如图,?ABCD的对角线相交于点O,过点O作EF⊥BD分别交AB,CD于点F,E,连接
DF,BE.请根据上述条件,写出一个正确结论.”有四位同学分别写出的结论如下:
小青:OE=OF;小何:四边形
DFBE是正方形;
小夏:S四边形AFED=S四边形FECB
;小雨:∠ACE=∠CAF.
这四位同学写出的结论中不正确的是(
)
A.小青
B.小何
C.小夏
D.小雨
三、解答题
8.如图,等边△AEF的顶点E,F在矩形ABCD的边BC,CD上,且∠CEF=45°.求证:矩形ABCD是正方形.
9.如图,在四边形ABFC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE.
(1)试判断四边形
BECF是什么四边形,并说明理由.
(2)当∠A的大小满足什么条件时,四边形BECF是正方形?请回答并证明你的结论.
B组(中档题)
四、填空题
10.如图,在四边形
ABCD
中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于点P.若四边形ABCD的面积是18,则
DP的长是______.
11.如图,已知AD是△ABC的角平分线,DE,DF分别是△ABD
和△ACD的高.给出下面四个结论:①OA=OD;②AD⊥EF;③当∠BAC=90°时,四边形AEDF是正方形;④AE2+DF2=AF2+DE2.其中正确的是______.(填序号)
12.如图,分别以△ABC的三边为边作等边△ACD,△ABE,△BCF,则下列结论:①△EBF≌△DFC;②四边形
AEFD为平行四边形;③当
AB=AC,且∠BAC=120°时,四边形
AEFD是正方形.其中正确的结论是______(请写出正确结论的序号).
五、解答题
13.如图,在平面直角坐标系中,点A是动点且纵坐标为4,点B是线段OA上的一个动点,过点B作直线MN平行于x轴,设MN分别交射线OA与x轴所成的两个角的平分线于点E,F.
(1)求证:EB=BF.
(2)当为何值时,四边形AEOF是矩形?证明你的结论.
(3)是否存在点A,B,使四边形AEOF为正方形?若存在,求点A与点B的坐标;若不存在,说明理由.
C组(综合题)
14.如图,四边形
ABCD为正方形,E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE,EF为邻边作矩形
DEFG,连接CG.
(1)求证:矩形
DEFG是正方形.
(2)若AB=2,CE=,求CG的长度.
(3)当线段DE与正方形ABCD
的某条边的夹角是30°时,直接写出∠EFC的度数.
参考答案
1.3.2正方形的判定
同步练习题
2021-2022学年北师大版九年级数学上册
A组(基础题)
一、填空题
1.(1)一个四边形满足对角线互相垂直平分且相等(答案不唯一)时,是正方形.
(2)一个平行四边形满足对角线互相垂直且相等(答案不唯一)时,是正方形.
(3)一个矩形满足对角线互相垂直(答案不唯一)时,是正方形.
(4)一个菱形满足对角线相等(答案不唯一)时,是正方形.
2.如图,将一张矩形纸片对折两次(两条折痕互相垂直),然后剪下一个角后,打开这个角,如果要剪出一个正方形,那么剪口线与折痕成45°角.
3.如图,在四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA
的中点.若使四边形EFGH为正方形,则四边形ABCD的对角线应具有的性质是垂直且相等.
二、选择题
4.如图,在菱形
ABCD中,对角线AC,BD交于点O,添加下列一个条件,能使菱形ABCD成为正方形的是(
C
)
A.BD=AB
B.AC=AD
C.∠ABC=90°
D.OD=AC
5.下列是关于某个四边形的三个结论:①它的对角线相等;②它是一个正方形;③它是一个矩形.下列推理过程正确的是(
A
)
A.由②推出③,由③推出①
B.由①推出②,由②推出③
C.由③推出①,由①推出②
D.由①推出③,由③推出②
6.如图所示,两个含30°角的完全相同的三角板ABC和三角板DEF沿直线l滑动,下列说法错误的是(
B
)
A.四边形ACDF是平行四边形
B.当点E为BC中点时,四边形ACDF是矩形
C.当点B与点E重合时,四边形ACDF是菱形
D.四边形ACDF不可能是正方形
7.在一次数学课上,张老师出示了一个题目:“如图,?ABCD的对角线相交于点O,过点O作EF⊥BD分别交AB,CD于点F,E,连接
DF,BE.请根据上述条件,写出一个正确结论.”有四位同学分别写出的结论如下:
小青:OE=OF;小何:四边形
DFBE是正方形;
小夏:S四边形AFED=S四边形FECB
;小雨:∠ACE=∠CAF.
这四位同学写出的结论中不正确的是(
B
)
A.小青
B.小何
C.小夏
D.小雨
三、解答题
8.如图,等边△AEF的顶点E,F在矩形ABCD的边BC,CD上,且∠CEF=45°.求证:矩形ABCD是正方形.
证明:∵四边形ABCD是矩形,
∴∠B=∠D=∠C=90°.
∵△AEF是等边三角形,
∴AE=AF,∠AEF=∠AFE=60°.
∵∠CEF=45°,∴∠CFE=∠CEF=45°.
∴∠AFD=∠AEB=180°-45°-60°=75°.
∴△AEB≌△AFD(AAS).
∴AB=AD.
∴矩形ABCD是正方形.
9.如图,在四边形ABFC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE.
(1)试判断四边形
BECF是什么四边形,并说明理由.
(2)当∠A的大小满足什么条件时,四边形BECF是正方形?请回答并证明你的结论.
解:(1)四边形BECF是菱形.理由如下:
∵EF垂直平分BC,
∴BF=FC,BE=EC.
∴∠EBC=∠ECB.
∵∠ACB=90°,
∴∠EBC+∠A=90°,∠ECB+∠ACE=90°.
∴∠A=∠ACE.∴EC=AE.
∴BE=AE.
又∵CF=AE.
∴BE=EC=CF=BF.
∴四边形BECF是菱形.
(2)当∠A=45°时,菱形BECF是正方形.
证明如下:∵∠ACE=∠A=45°,∴∠CEA=90°.
∵四边形BECF是菱形,
∴四边形BECF是正方形.
故当∠A=45°时,四边形BECF是正方形.
B组(中档题)
四、填空题
10.如图,在四边形
ABCD
中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于点P.若四边形ABCD的面积是18,则
DP的长是3.
11.如图,已知AD是△ABC的角平分线,DE,DF分别是△ABD
和△ACD的高.给出下面四个结论:①OA=OD;②AD⊥EF;③当∠BAC=90°时,四边形AEDF是正方形;④AE2+DF2=AF2+DE2.其中正确的是②③④.(填序号)
12.如图,分别以△ABC的三边为边作等边△ACD,△ABE,△BCF,则下列结论:①△EBF≌△DFC;②四边形
AEFD为平行四边形;③当
AB=AC,且∠BAC=120°时,四边形
AEFD是正方形.其中正确的结论是①②(请写出正确结论的序号).
五、解答题
13.如图,在平面直角坐标系中,点A是动点且纵坐标为4,点B是线段OA上的一个动点,过点B作直线MN平行于x轴,设MN分别交射线OA与x轴所成的两个角的平分线于点E,F.
(1)求证:EB=BF.
(2)当为何值时,四边形AEOF是矩形?证明你的结论.
(3)是否存在点A,B,使四边形AEOF为正方形?若存在,求点A与点B的坐标;若不存在,说明理由.
解:(1)证明:∵OF是∠AOx的平分线,∴∠AOF=∠FOx,
∵MN∥x轴,∴∠MFO=∠FOx,
∴∠AOF=∠MFO.∴BO=BF.
同理:BO=BE,
∴EB=BF.
(2)当=,四边形AEOF是矩形.
证明:∵=,∴OB=AB.
又∵BE=BF,
∴四边形AEOF是平行四边形.
∵OE,OF是角平分线,∴∠EOF=90°,
∴四边形AEOF是矩形.
(3)存在点A,B使四边形AEOF为正方形,
∵MN∥x轴,
∴当A点在y轴时,即A点坐标为(0,4)时,有OA⊥EF,此时,取OA的中点B(0,2),由(2)知四边形AEOF是矩形.
∴四边形AEOF为正方形.
∴存在A(0,4),B(0,2),使四边形AEOF为正方形.
C组(综合题)
14.如图,四边形
ABCD为正方形,E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE,EF为邻边作矩形
DEFG,连接CG.
(1)求证:矩形
DEFG是正方形.
(2)若AB=2,CE=,求CG的长度.
(3)当线段DE与正方形ABCD
的某条边的夹角是30°时,直接写出∠EFC的度数.
解:(1)证明:过点E作EP⊥CD于点P,EQ⊥BC于点Q.
∴∠EQF=∠EPD.
∵四边形ABCD是正方形,
∴∠DCA=∠BCA.
∴EQ=EP,∠QEC=∠PEC=45°.
∴∠QEF+∠FEC=45°.
∵四边形DEFG是矩形,
∴∠DEF=90°.
∴∠PED+∠FEC=45°.
∴∠QEF=∠PED.
∴△EQF≌△EPD(ASA).
∴EF=ED.
∴矩形DEFG是正方形.
(2)在Rt△ABC中,AC==AB=2.
∵CE=,∴AE=CE=AC.
∴点F与点C重合,此时△DCG是等腰直角三角形,易知CG=.
(3)①当DE与AD的夹角为30°时,∠EFC=120°;
②当DE与
DC的夹角为30°时,∠EFC=30°.
综上所述,∠EFC=120°或30°.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
