2021-2022学年北师大版九年级数学上册第三章 概率的进一步认识 单元同步练习题(word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学上册第三章 概率的进一步认识 单元同步练习题(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 104.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-23 08:03:59 | ||
图片预览




文档简介
2021-2022学年北师大版九年级数学上册第三章
概率的进一步认识
单元同步练习题
一、填空题
1.某校开展以“我和我的祖国”为主题的“大合唱”活动,七年级准备从小明、小东、小聪三名男生和小红、小慧两名女生中各随机选出一名男生和一名女生担任领唱,则小聪和小慧被同时选中的概率是______.
2.在一只不透明的袋中,装着标有数字3,4,5,7的质地、大小均相同的小球.小明和小东同时从袋中随机各摸出1个球,并计算这两球上的数字之和,当和小于9时小明获胜,反之小东获胜,则小东获胜的概率为______.
3.如图,在?ABCD中,E为BC的中点,BD,AE交于点O.若随机向?ABCD内投一粒米,则米粒落在图中阴影部分的概率为______.
4.如图,正方形ABCD内的图形来自中国古代的太极图,现随机向正方形内掷一枚小针,则针尖落在黑色区域内的概率为______.
5.汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”是我国古代数学的瑰宝.如图所示的弦图中,四个直角三角形都是全等的,它们的两直角边之比均为2∶3.现随机向该图形内掷一枚小针,则针尖落在阴影区域的概率为______.
6.在一个不透明的布袋中装有黄、白两种颜色的球共40个,除颜色外其他都相同,小王通过多次摸球试验后发现,摸到黄球的频率稳定在0.35左右,则布袋中黄球可能有______个.
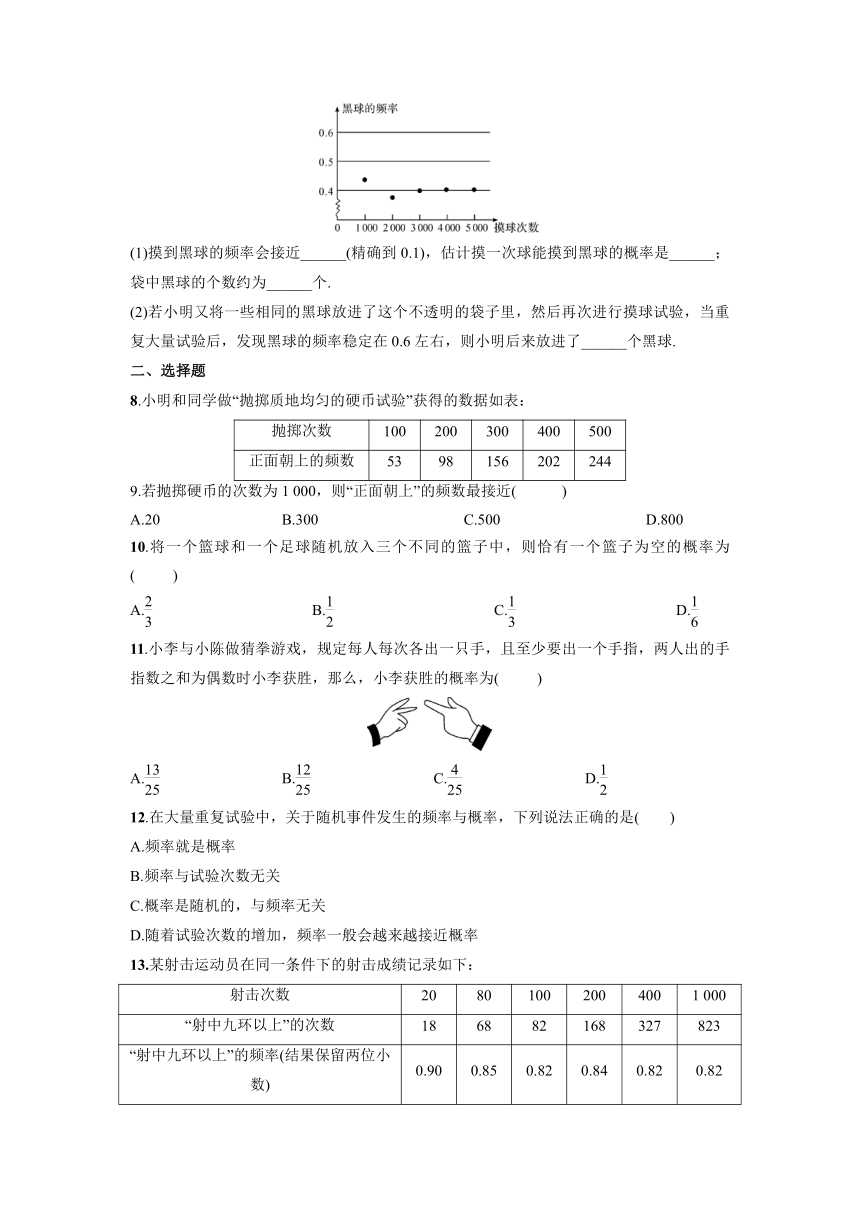
7.一个不透明的袋子里装有黑、白两种颜色的球共50个,这些球除颜色外都相同.小明从袋子中随机摸一个球,记下颜色后放回,不断重复,并绘制了如图所示的统计图,根据统计图提供的信息解决下列问题:
(1)摸到黑球的频率会接近______(精确到0.1),估计摸一次球能摸到黑球的概率是______;袋中黑球的个数约为______个.
(2)若小明又将一些相同的黑球放进了这个不透明的袋子里,然后再次进行摸球试验,当重复大量试验后,发现黑球的频率稳定在0.6左右,则小明后来放进了______个黑球.
二、选择题
8.小明和同学做“抛掷质地均匀的硬币试验”获得的数据如表:
抛掷次数
100
200
300
400
500
正面朝上的频数
53
98
156
202
244
9.若抛掷硬币的次数为1
000,则“正面朝上”的频数最接近(
)
A.20
B.300
C.500
D.800
10.将一个篮球和一个足球随机放入三个不同的篮子中,则恰有一个篮子为空的概率为(
)
A.
B.
C.
D.
11.小李与小陈做猜拳游戏,规定每人每次各出一只手,且至少要出一个手指,两人出的手指数之和为偶数时小李获胜,那么,小李获胜的概率为(
)
A.
B.
C.
D.
12.在大量重复试验中,关于随机事件发生的频率与概率,下列说法正确的是(
)
A.频率就是概率
B.频率与试验次数无关
C.概率是随机的,与频率无关
D.随着试验次数的增加,频率一般会越来越接近概率
13.某射击运动员在同一条件下的射击成绩记录如下:
射击次数
20
80
100
200
400
1
000
“射中九环以上”的次数
18
68
82
168
327
823
“射中九环以上”的频率(结果保留两位小数)
0.90
0.85
0.82
0.84
0.82
0.82
根据频率的稳定性,估计这名运动员射击一次时“射中九环以上”的概率约是(
)
A.0.90
B.0.82
C.0.85
D.0.84
14.为了估计水塘中的鱼数,养鱼者首先从鱼塘中捕获20条鱼,在每条鱼身上做好记号后,把这些鱼放归鱼塘.再从鱼塘中打捞100条鱼,如果在这100条鱼中有5条鱼是有记号的,则估计该鱼塘中的鱼数约为(
)
A.300条
B.380条
C.400条
D.420条
三、解答题
15.一只不透明的口袋中放有若干个红球和白球,这两种球除了颜色以外没有任何其他区别,将袋中的球摇均匀.每次从口袋中取出一个球记录颜色后放回再摇均匀,经过大量的试验,得到取出红球的频率是.
(1)取出白球的概率是多少?
(2)如果袋中的白球有18个,那么袋中的红球有多少个?
16.“每天锻炼一小时,健康生活一辈子.”为了选拔“阳光大课间”领操员,学校组织初中三个年级推选出来的15名领操员进行比赛,成绩如下表:
成绩/分
7
8
9
10
人数/人
2
5
4
4
(1)这组数据的众数是8,中位数是9.
(2)已知获得10分的选手中,七、八、九年级分别有1人、2人、1人,学校准备从中随机抽取两人领操,求恰好抽到八年级两名领操员的概率.
17.王强与李刚两位同学在学习“概率”时,做抛骰子(均匀正方体形状)试验,他们共抛了54次,出现向上点数的次数如下表:
向上点数
1
2
3
4
5
6
出现次数
6
9
5
8
16
10
(1)请计算出现向上点数为3的频率及出现向上点数为5的频率.
(2)王强说:“根据试验,一次试验中出现向上点数为5的概率最大.”李刚说:“如果抛540次,那么出现向上点数为6的次数正好是100次.”请判断王强和李刚说法的对错.
(3)如果王强与李刚各抛一枚骰子,求出现向上点数之和为3的倍数的概率.
18.下面是两个转盘,每个转盘均分成几个形状相同的扇形,甲、乙两个人做游戏,游戏者同时转动两个转盘一次,若转盘A转出了红色,转盘B转出了蓝色,则甲赢,否则乙赢.
(1)甲和乙获胜的概率分别是多少?
(2)这个游戏对双方公平吗?说说你的理由.
(3)如果你认为不公平,应怎样修改才能使游戏对双方都公平?
转盘A 转盘B
19.小红和小明在操场做游戏,他们先在地上画了半径分别2
m和3
m的同心圆(如图),蒙上眼在一定距离外向圈内掷小石子,掷中阴影小红胜,否则小明胜,未掷入圈内不算,你来当裁判.
(1)你认为游戏公平吗?为什么?
(2)游戏结束,小明边走边想,“反过来,能否用频率估计概率的方法,来估算某一不规则图形的面积呢?”.请你设计方案,解决这一问题.(要求补充完整图形,说明设计步骤、原理,写出估算公式)
参考答案
2021-2022学年北师大版九年级数学上册第三章
概率的进一步认识
单元同步练习题
一、填空题
1.某校开展以“我和我的祖国”为主题的“大合唱”活动,七年级准备从小明、小东、小聪三名男生和小红、小慧两名女生中各随机选出一名男生和一名女生担任领唱,则小聪和小慧被同时选中的概率是.
2.在一只不透明的袋中,装着标有数字3,4,5,7的质地、大小均相同的小球.小明和小东同时从袋中随机各摸出1个球,并计算这两球上的数字之和,当和小于9时小明获胜,反之小东获胜,则小东获胜的概率为.
3.如图,在?ABCD中,E为BC的中点,BD,AE交于点O.若随机向?ABCD内投一粒米,则米粒落在图中阴影部分的概率为.
4.如图,正方形ABCD内的图形来自中国古代的太极图,现随机向正方形内掷一枚小针,则针尖落在黑色区域内的概率为.
5.汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”是我国古代数学的瑰宝.如图所示的弦图中,四个直角三角形都是全等的,它们的两直角边之比均为2∶3.现随机向该图形内掷一枚小针,则针尖落在阴影区域的概率为.
6.在一个不透明的布袋中装有黄、白两种颜色的球共40个,除颜色外其他都相同,小王通过多次摸球试验后发现,摸到黄球的频率稳定在0.35左右,则布袋中黄球可能有14个.
7.一个不透明的袋子里装有黑、白两种颜色的球共50个,这些球除颜色外都相同.小明从袋子中随机摸一个球,记下颜色后放回,不断重复,并绘制了如图所示的统计图,根据统计图提供的信息解决下列问题:
(1)摸到黑球的频率会接近0.4(精确到0.1),估计摸一次球能摸到黑球的概率是0.4;袋中黑球的个数约为20个.
(2)若小明又将一些相同的黑球放进了这个不透明的袋子里,然后再次进行摸球试验,当重复大量试验后,发现黑球的频率稳定在0.6左右,则小明后来放进了25个黑球.
二、选择题
8.小明和同学做“抛掷质地均匀的硬币试验”获得的数据如表:
抛掷次数
100
200
300
400
500
正面朝上的频数
53
98
156
202
244
9.若抛掷硬币的次数为1
000,则“正面朝上”的频数最接近(
C
)
A.20
B.300
C.500
D.800
10.将一个篮球和一个足球随机放入三个不同的篮子中,则恰有一个篮子为空的概率为(
A
)
A.
B.
C.
D.
11.小李与小陈做猜拳游戏,规定每人每次各出一只手,且至少要出一个手指,两人出的手指数之和为偶数时小李获胜,那么,小李获胜的概率为(
A
)
A.
B.
C.
D.
12.在大量重复试验中,关于随机事件发生的频率与概率,下列说法正确的是(
D
)
A.频率就是概率
B.频率与试验次数无关
C.概率是随机的,与频率无关
D.随着试验次数的增加,频率一般会越来越接近概率
13.某射击运动员在同一条件下的射击成绩记录如下:
射击次数
20
80
100
200
400
1
000
“射中九环以上”的次数
18
68
82
168
327
823
“射中九环以上”的频率(结果保留两位小数)
0.90
0.85
0.82
0.84
0.82
0.82
根据频率的稳定性,估计这名运动员射击一次时“射中九环以上”的概率约是(
B
)
A.0.90
B.0.82
C.0.85
D.0.84
14.为了估计水塘中的鱼数,养鱼者首先从鱼塘中捕获20条鱼,在每条鱼身上做好记号后,把这些鱼放归鱼塘.再从鱼塘中打捞100条鱼,如果在这100条鱼中有5条鱼是有记号的,则估计该鱼塘中的鱼数约为(
C
)
A.300条
B.380条
C.400条
D.420条
三、解答题
15.一只不透明的口袋中放有若干个红球和白球,这两种球除了颜色以外没有任何其他区别,将袋中的球摇均匀.每次从口袋中取出一个球记录颜色后放回再摇均匀,经过大量的试验,得到取出红球的频率是.
(1)取出白球的概率是多少?
(2)如果袋中的白球有18个,那么袋中的红球有多少个?
解:(1)P(取出白球)=1-=.
(2)设袋中有红球x个,则
=,解得x=6.
经检验,x=6是原方程的解.
答:袋中有6个红球.
16.“每天锻炼一小时,健康生活一辈子.”为了选拔“阳光大课间”领操员,学校组织初中三个年级推选出来的15名领操员进行比赛,成绩如下表:
成绩/分
7
8
9
10
人数/人
2
5
4
4
(1)这组数据的众数是8,中位数是9.
(2)已知获得10分的选手中,七、八、九年级分别有1人、2人、1人,学校准备从中随机抽取两人领操,求恰好抽到八年级两名领操员的概率.
解:画树状图如下:
由树状图可知,共有12种等可能的结果,其中恰好抽到八年级两名领操员的结果有2种,
所以P(恰好抽到八年级两名领操员)==.
17.王强与李刚两位同学在学习“概率”时,做抛骰子(均匀正方体形状)试验,他们共抛了54次,出现向上点数的次数如下表:
向上点数
1
2
3
4
5
6
出现次数
6
9
5
8
16
10
(1)请计算出现向上点数为3的频率及出现向上点数为5的频率.
(2)王强说:“根据试验,一次试验中出现向上点数为5的概率最大.”李刚说:“如果抛540次,那么出现向上点数为6的次数正好是100次.”请判断王强和李刚说法的对错.
(3)如果王强与李刚各抛一枚骰子,求出现向上点数之和为3的倍数的概率.
解:(1)点数为3的概率是,点数为5的频率是.
(2)他们的说法均错.
(3)点数之和为3的倍数的概率为.
18.下面是两个转盘,每个转盘均分成几个形状相同的扇形,甲、乙两个人做游戏,游戏者同时转动两个转盘一次,若转盘A转出了红色,转盘B转出了蓝色,则甲赢,否则乙赢.
(1)甲和乙获胜的概率分别是多少?
(2)这个游戏对双方公平吗?说说你的理由.
(3)如果你认为不公平,应怎样修改才能使游戏对双方都公平?
转盘A 转盘B
解:(1)列表如下:
A
B
红
红
红
红
蓝
蓝
蓝、红
蓝、红
蓝、红
蓝、红
蓝、蓝
蓝
蓝、红
蓝、红
蓝、红
蓝、红
蓝、蓝
蓝
蓝、红
蓝、红
蓝、红
蓝、红
蓝、蓝
蓝
蓝、红
蓝、红
蓝、红
蓝、红
蓝、蓝
红
红、红
红、红
红、红
红、红
红、蓝
由表知,共有25种等可能结果,其中转盘A转出了红色,转盘B转出了蓝色的结果有16种,
∴甲获胜的概率为,则乙获胜的概率为.
(2)不公平.理由:
因为≠.
所以甲、乙获胜的概率不相等.
(3)两个转盘都转出蓝色,甲赢;两个转盘都转出红色,乙赢.
19.小红和小明在操场做游戏,他们先在地上画了半径分别2
m和3
m的同心圆(如图),蒙上眼在一定距离外向圈内掷小石子,掷中阴影小红胜,否则小明胜,未掷入圈内不算,你来当裁判.
(1)你认为游戏公平吗?为什么?
(2)游戏结束,小明边走边想,“反过来,能否用频率估计概率的方法,来估算某一不规则图形的面积呢?”.请你设计方案,解决这一问题.(要求补充完整图形,说明设计步骤、原理,写出估算公式)
解:(1)不公平.
∵P(阴)==,
即小红胜率为,小明胜率为.
∴游戏对双方不公平.
(2)能利用频率估计概率的实验方法估算不规则图形的面积.
设计方案:①设计一个可测量面积的规则图形将不规则图形围起来(如正方形,其面积为S).如图所示:
②往图形中掷点(如蒙上眼往图形中随意掷石子,掷在图外不作记录).
③当掷点数充分大(如1万次),记录并统计结果,设掷入正方形内m次,其中n次掷进不规则图形内.
④设不规则图形的面积为S1,用频率估计概率,
即频率P′(掷入不规则图形内)=≈概率P(掷入不规则图形内)=,
∴≈.∴S1≈.
概率的进一步认识
单元同步练习题
一、填空题
1.某校开展以“我和我的祖国”为主题的“大合唱”活动,七年级准备从小明、小东、小聪三名男生和小红、小慧两名女生中各随机选出一名男生和一名女生担任领唱,则小聪和小慧被同时选中的概率是______.
2.在一只不透明的袋中,装着标有数字3,4,5,7的质地、大小均相同的小球.小明和小东同时从袋中随机各摸出1个球,并计算这两球上的数字之和,当和小于9时小明获胜,反之小东获胜,则小东获胜的概率为______.
3.如图,在?ABCD中,E为BC的中点,BD,AE交于点O.若随机向?ABCD内投一粒米,则米粒落在图中阴影部分的概率为______.
4.如图,正方形ABCD内的图形来自中国古代的太极图,现随机向正方形内掷一枚小针,则针尖落在黑色区域内的概率为______.
5.汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”是我国古代数学的瑰宝.如图所示的弦图中,四个直角三角形都是全等的,它们的两直角边之比均为2∶3.现随机向该图形内掷一枚小针,则针尖落在阴影区域的概率为______.
6.在一个不透明的布袋中装有黄、白两种颜色的球共40个,除颜色外其他都相同,小王通过多次摸球试验后发现,摸到黄球的频率稳定在0.35左右,则布袋中黄球可能有______个.
7.一个不透明的袋子里装有黑、白两种颜色的球共50个,这些球除颜色外都相同.小明从袋子中随机摸一个球,记下颜色后放回,不断重复,并绘制了如图所示的统计图,根据统计图提供的信息解决下列问题:
(1)摸到黑球的频率会接近______(精确到0.1),估计摸一次球能摸到黑球的概率是______;袋中黑球的个数约为______个.
(2)若小明又将一些相同的黑球放进了这个不透明的袋子里,然后再次进行摸球试验,当重复大量试验后,发现黑球的频率稳定在0.6左右,则小明后来放进了______个黑球.
二、选择题
8.小明和同学做“抛掷质地均匀的硬币试验”获得的数据如表:
抛掷次数
100
200
300
400
500
正面朝上的频数
53
98
156
202
244
9.若抛掷硬币的次数为1
000,则“正面朝上”的频数最接近(
)
A.20
B.300
C.500
D.800
10.将一个篮球和一个足球随机放入三个不同的篮子中,则恰有一个篮子为空的概率为(
)
A.
B.
C.
D.
11.小李与小陈做猜拳游戏,规定每人每次各出一只手,且至少要出一个手指,两人出的手指数之和为偶数时小李获胜,那么,小李获胜的概率为(
)
A.
B.
C.
D.
12.在大量重复试验中,关于随机事件发生的频率与概率,下列说法正确的是(
)
A.频率就是概率
B.频率与试验次数无关
C.概率是随机的,与频率无关
D.随着试验次数的增加,频率一般会越来越接近概率
13.某射击运动员在同一条件下的射击成绩记录如下:
射击次数
20
80
100
200
400
1
000
“射中九环以上”的次数
18
68
82
168
327
823
“射中九环以上”的频率(结果保留两位小数)
0.90
0.85
0.82
0.84
0.82
0.82
根据频率的稳定性,估计这名运动员射击一次时“射中九环以上”的概率约是(
)
A.0.90
B.0.82
C.0.85
D.0.84
14.为了估计水塘中的鱼数,养鱼者首先从鱼塘中捕获20条鱼,在每条鱼身上做好记号后,把这些鱼放归鱼塘.再从鱼塘中打捞100条鱼,如果在这100条鱼中有5条鱼是有记号的,则估计该鱼塘中的鱼数约为(
)
A.300条
B.380条
C.400条
D.420条
三、解答题
15.一只不透明的口袋中放有若干个红球和白球,这两种球除了颜色以外没有任何其他区别,将袋中的球摇均匀.每次从口袋中取出一个球记录颜色后放回再摇均匀,经过大量的试验,得到取出红球的频率是.
(1)取出白球的概率是多少?
(2)如果袋中的白球有18个,那么袋中的红球有多少个?
16.“每天锻炼一小时,健康生活一辈子.”为了选拔“阳光大课间”领操员,学校组织初中三个年级推选出来的15名领操员进行比赛,成绩如下表:
成绩/分
7
8
9
10
人数/人
2
5
4
4
(1)这组数据的众数是8,中位数是9.
(2)已知获得10分的选手中,七、八、九年级分别有1人、2人、1人,学校准备从中随机抽取两人领操,求恰好抽到八年级两名领操员的概率.
17.王强与李刚两位同学在学习“概率”时,做抛骰子(均匀正方体形状)试验,他们共抛了54次,出现向上点数的次数如下表:
向上点数
1
2
3
4
5
6
出现次数
6
9
5
8
16
10
(1)请计算出现向上点数为3的频率及出现向上点数为5的频率.
(2)王强说:“根据试验,一次试验中出现向上点数为5的概率最大.”李刚说:“如果抛540次,那么出现向上点数为6的次数正好是100次.”请判断王强和李刚说法的对错.
(3)如果王强与李刚各抛一枚骰子,求出现向上点数之和为3的倍数的概率.
18.下面是两个转盘,每个转盘均分成几个形状相同的扇形,甲、乙两个人做游戏,游戏者同时转动两个转盘一次,若转盘A转出了红色,转盘B转出了蓝色,则甲赢,否则乙赢.
(1)甲和乙获胜的概率分别是多少?
(2)这个游戏对双方公平吗?说说你的理由.
(3)如果你认为不公平,应怎样修改才能使游戏对双方都公平?
转盘A 转盘B
19.小红和小明在操场做游戏,他们先在地上画了半径分别2
m和3
m的同心圆(如图),蒙上眼在一定距离外向圈内掷小石子,掷中阴影小红胜,否则小明胜,未掷入圈内不算,你来当裁判.
(1)你认为游戏公平吗?为什么?
(2)游戏结束,小明边走边想,“反过来,能否用频率估计概率的方法,来估算某一不规则图形的面积呢?”.请你设计方案,解决这一问题.(要求补充完整图形,说明设计步骤、原理,写出估算公式)
参考答案
2021-2022学年北师大版九年级数学上册第三章
概率的进一步认识
单元同步练习题
一、填空题
1.某校开展以“我和我的祖国”为主题的“大合唱”活动,七年级准备从小明、小东、小聪三名男生和小红、小慧两名女生中各随机选出一名男生和一名女生担任领唱,则小聪和小慧被同时选中的概率是.
2.在一只不透明的袋中,装着标有数字3,4,5,7的质地、大小均相同的小球.小明和小东同时从袋中随机各摸出1个球,并计算这两球上的数字之和,当和小于9时小明获胜,反之小东获胜,则小东获胜的概率为.
3.如图,在?ABCD中,E为BC的中点,BD,AE交于点O.若随机向?ABCD内投一粒米,则米粒落在图中阴影部分的概率为.
4.如图,正方形ABCD内的图形来自中国古代的太极图,现随机向正方形内掷一枚小针,则针尖落在黑色区域内的概率为.
5.汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”是我国古代数学的瑰宝.如图所示的弦图中,四个直角三角形都是全等的,它们的两直角边之比均为2∶3.现随机向该图形内掷一枚小针,则针尖落在阴影区域的概率为.
6.在一个不透明的布袋中装有黄、白两种颜色的球共40个,除颜色外其他都相同,小王通过多次摸球试验后发现,摸到黄球的频率稳定在0.35左右,则布袋中黄球可能有14个.
7.一个不透明的袋子里装有黑、白两种颜色的球共50个,这些球除颜色外都相同.小明从袋子中随机摸一个球,记下颜色后放回,不断重复,并绘制了如图所示的统计图,根据统计图提供的信息解决下列问题:
(1)摸到黑球的频率会接近0.4(精确到0.1),估计摸一次球能摸到黑球的概率是0.4;袋中黑球的个数约为20个.
(2)若小明又将一些相同的黑球放进了这个不透明的袋子里,然后再次进行摸球试验,当重复大量试验后,发现黑球的频率稳定在0.6左右,则小明后来放进了25个黑球.
二、选择题
8.小明和同学做“抛掷质地均匀的硬币试验”获得的数据如表:
抛掷次数
100
200
300
400
500
正面朝上的频数
53
98
156
202
244
9.若抛掷硬币的次数为1
000,则“正面朝上”的频数最接近(
C
)
A.20
B.300
C.500
D.800
10.将一个篮球和一个足球随机放入三个不同的篮子中,则恰有一个篮子为空的概率为(
A
)
A.
B.
C.
D.
11.小李与小陈做猜拳游戏,规定每人每次各出一只手,且至少要出一个手指,两人出的手指数之和为偶数时小李获胜,那么,小李获胜的概率为(
A
)
A.
B.
C.
D.
12.在大量重复试验中,关于随机事件发生的频率与概率,下列说法正确的是(
D
)
A.频率就是概率
B.频率与试验次数无关
C.概率是随机的,与频率无关
D.随着试验次数的增加,频率一般会越来越接近概率
13.某射击运动员在同一条件下的射击成绩记录如下:
射击次数
20
80
100
200
400
1
000
“射中九环以上”的次数
18
68
82
168
327
823
“射中九环以上”的频率(结果保留两位小数)
0.90
0.85
0.82
0.84
0.82
0.82
根据频率的稳定性,估计这名运动员射击一次时“射中九环以上”的概率约是(
B
)
A.0.90
B.0.82
C.0.85
D.0.84
14.为了估计水塘中的鱼数,养鱼者首先从鱼塘中捕获20条鱼,在每条鱼身上做好记号后,把这些鱼放归鱼塘.再从鱼塘中打捞100条鱼,如果在这100条鱼中有5条鱼是有记号的,则估计该鱼塘中的鱼数约为(
C
)
A.300条
B.380条
C.400条
D.420条
三、解答题
15.一只不透明的口袋中放有若干个红球和白球,这两种球除了颜色以外没有任何其他区别,将袋中的球摇均匀.每次从口袋中取出一个球记录颜色后放回再摇均匀,经过大量的试验,得到取出红球的频率是.
(1)取出白球的概率是多少?
(2)如果袋中的白球有18个,那么袋中的红球有多少个?
解:(1)P(取出白球)=1-=.
(2)设袋中有红球x个,则
=,解得x=6.
经检验,x=6是原方程的解.
答:袋中有6个红球.
16.“每天锻炼一小时,健康生活一辈子.”为了选拔“阳光大课间”领操员,学校组织初中三个年级推选出来的15名领操员进行比赛,成绩如下表:
成绩/分
7
8
9
10
人数/人
2
5
4
4
(1)这组数据的众数是8,中位数是9.
(2)已知获得10分的选手中,七、八、九年级分别有1人、2人、1人,学校准备从中随机抽取两人领操,求恰好抽到八年级两名领操员的概率.
解:画树状图如下:
由树状图可知,共有12种等可能的结果,其中恰好抽到八年级两名领操员的结果有2种,
所以P(恰好抽到八年级两名领操员)==.
17.王强与李刚两位同学在学习“概率”时,做抛骰子(均匀正方体形状)试验,他们共抛了54次,出现向上点数的次数如下表:
向上点数
1
2
3
4
5
6
出现次数
6
9
5
8
16
10
(1)请计算出现向上点数为3的频率及出现向上点数为5的频率.
(2)王强说:“根据试验,一次试验中出现向上点数为5的概率最大.”李刚说:“如果抛540次,那么出现向上点数为6的次数正好是100次.”请判断王强和李刚说法的对错.
(3)如果王强与李刚各抛一枚骰子,求出现向上点数之和为3的倍数的概率.
解:(1)点数为3的概率是,点数为5的频率是.
(2)他们的说法均错.
(3)点数之和为3的倍数的概率为.
18.下面是两个转盘,每个转盘均分成几个形状相同的扇形,甲、乙两个人做游戏,游戏者同时转动两个转盘一次,若转盘A转出了红色,转盘B转出了蓝色,则甲赢,否则乙赢.
(1)甲和乙获胜的概率分别是多少?
(2)这个游戏对双方公平吗?说说你的理由.
(3)如果你认为不公平,应怎样修改才能使游戏对双方都公平?
转盘A 转盘B
解:(1)列表如下:
A
B
红
红
红
红
蓝
蓝
蓝、红
蓝、红
蓝、红
蓝、红
蓝、蓝
蓝
蓝、红
蓝、红
蓝、红
蓝、红
蓝、蓝
蓝
蓝、红
蓝、红
蓝、红
蓝、红
蓝、蓝
蓝
蓝、红
蓝、红
蓝、红
蓝、红
蓝、蓝
红
红、红
红、红
红、红
红、红
红、蓝
由表知,共有25种等可能结果,其中转盘A转出了红色,转盘B转出了蓝色的结果有16种,
∴甲获胜的概率为,则乙获胜的概率为.
(2)不公平.理由:
因为≠.
所以甲、乙获胜的概率不相等.
(3)两个转盘都转出蓝色,甲赢;两个转盘都转出红色,乙赢.
19.小红和小明在操场做游戏,他们先在地上画了半径分别2
m和3
m的同心圆(如图),蒙上眼在一定距离外向圈内掷小石子,掷中阴影小红胜,否则小明胜,未掷入圈内不算,你来当裁判.
(1)你认为游戏公平吗?为什么?
(2)游戏结束,小明边走边想,“反过来,能否用频率估计概率的方法,来估算某一不规则图形的面积呢?”.请你设计方案,解决这一问题.(要求补充完整图形,说明设计步骤、原理,写出估算公式)
解:(1)不公平.
∵P(阴)==,
即小红胜率为,小明胜率为.
∴游戏对双方不公平.
(2)能利用频率估计概率的实验方法估算不规则图形的面积.
设计方案:①设计一个可测量面积的规则图形将不规则图形围起来(如正方形,其面积为S).如图所示:
②往图形中掷点(如蒙上眼往图形中随意掷石子,掷在图外不作记录).
③当掷点数充分大(如1万次),记录并统计结果,设掷入正方形内m次,其中n次掷进不规则图形内.
④设不规则图形的面积为S1,用频率估计概率,
即频率P′(掷入不规则图形内)=≈概率P(掷入不规则图形内)=,
∴≈.∴S1≈.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
