2020-2021学年湖南省长沙市天心区九年级(下)期中数学试卷(word解析版)
文档属性
| 名称 | 2020-2021学年湖南省长沙市天心区九年级(下)期中数学试卷(word解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 538.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-21 16:46:23 | ||
图片预览



文档简介
2020-2021学年湖南省长沙市天心区九年级(下)期中数学试卷
一、选择题(本大题共12小题,每小题3分,共36分)
1.(3分)下列实数是无理数的是( )
A.0
B.
C.
D.
2.(3分)下列图形中,既是轴对称图形又是中心对称图形的是( )
A.
B.
C.
D.
3.(3分)2021年2月27日,岳麓山多个地方人头攒动,当日麓山景区接待游客122700人次,高居全省各景区第一位,其中122700用科学记数法表示为( )
A.1.227×105
B.1.227×106
C.1.227×104
D.0.1227×107
4.(3分)下列计算中,正确的是( )
A.(a2)3=a5
B.3a﹣2a=1
C.(3a)2=9a
D.a?a2=a3
5.(3分)已知关于x的一元二次方程x2﹣4x+c=0有两个相等的实数根,则c=( )
A.4
B.2
C.1
D.﹣4
6.(3分)圆锥的底面圆的半径r=3,高h=4,则圆锥的侧面积是( )
A.10π
B.15π
C.30π
D.45π
7.(3分)不等式组的解在数轴上表示为( )
A.
B.
C.
D.
8.(3分)如图,在直角坐标系中,点A是x轴正半轴上的一个定点,点B是双曲线(x>0)上的一个动点,当点B的横坐标逐渐增大时,△OAB的面积将会( )
A.逐渐增大
B.不变
C.逐渐减小
D.先增大后减小
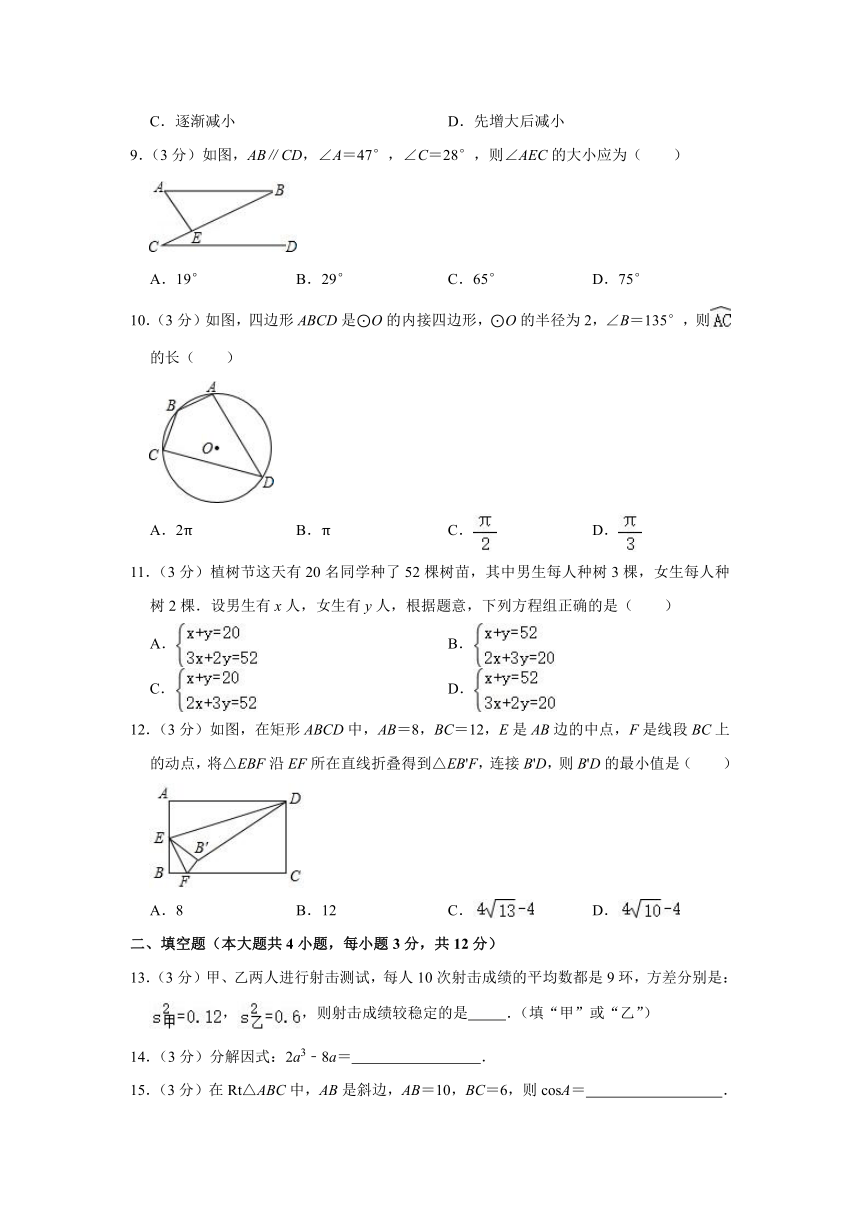
9.(3分)如图,AB∥CD,∠A=47°,∠C=28°,则∠AEC的大小应为( )
A.19°
B.29°
C.65°
D.75°
10.(3分)如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为2,∠B=135°,则的长( )
A.2π
B.π
C.
D.
11.(3分)植树节这天有20名同学种了52棵树苗,其中男生每人种树3棵,女生每人种树2棵.设男生有x人,女生有y人,根据题意,下列方程组正确的是( )
A.
B.
C.
D.
12.(3分)如图,在矩形ABCD中,AB=8,BC=12,E是AB边的中点,F是线段BC上的动点,将△EBF沿EF所在直线折叠得到△EB'F,连接B'D,则B'D的最小值是( )
A.8
B.12
C.
D.
二、填空题(本大题共4小题,每小题3分,共12分)
13.(3分)甲、乙两人进行射击测试,每人10次射击成绩的平均数都是9环,方差分别是:,,则射击成绩较稳定的是
.(填“甲”或“乙”)
14.(3分)分解因式:2a3﹣8a=
.
15.(3分)在Rt△ABC中,AB是斜边,AB=10,BC=6,则cosA=
.
16.(3分)已知二次函数y=ax2+bx+c(a,b,c为整数且a≠0),对一切实数x恒有x≤y≤2x2+,则其解析式为
.
三、解答题(本大题共9小题,共72分,解答应写出必要文字说明、证明过程或演算步骤)
17.(6分)计算:.
18.(6分)先化简,再求值:(x﹣2y)2﹣x(x﹣4y),其中,x=1,y=﹣1.
19.(6分)已知:如图,在△ABC中,∠C=90°.
(1)作图题:在AC边上,找一个点D,使点D到AB的距离等于DC,下列选项中,选出作法正确的
;
①取AC的中点D;
②用尺规作角B的平分线,交AC于点D;
③用尺规作AB边的中垂线,交AC或其延长线于点D;
(2)在(1)的条件下,若AB=5,AC=4,求CD的长.
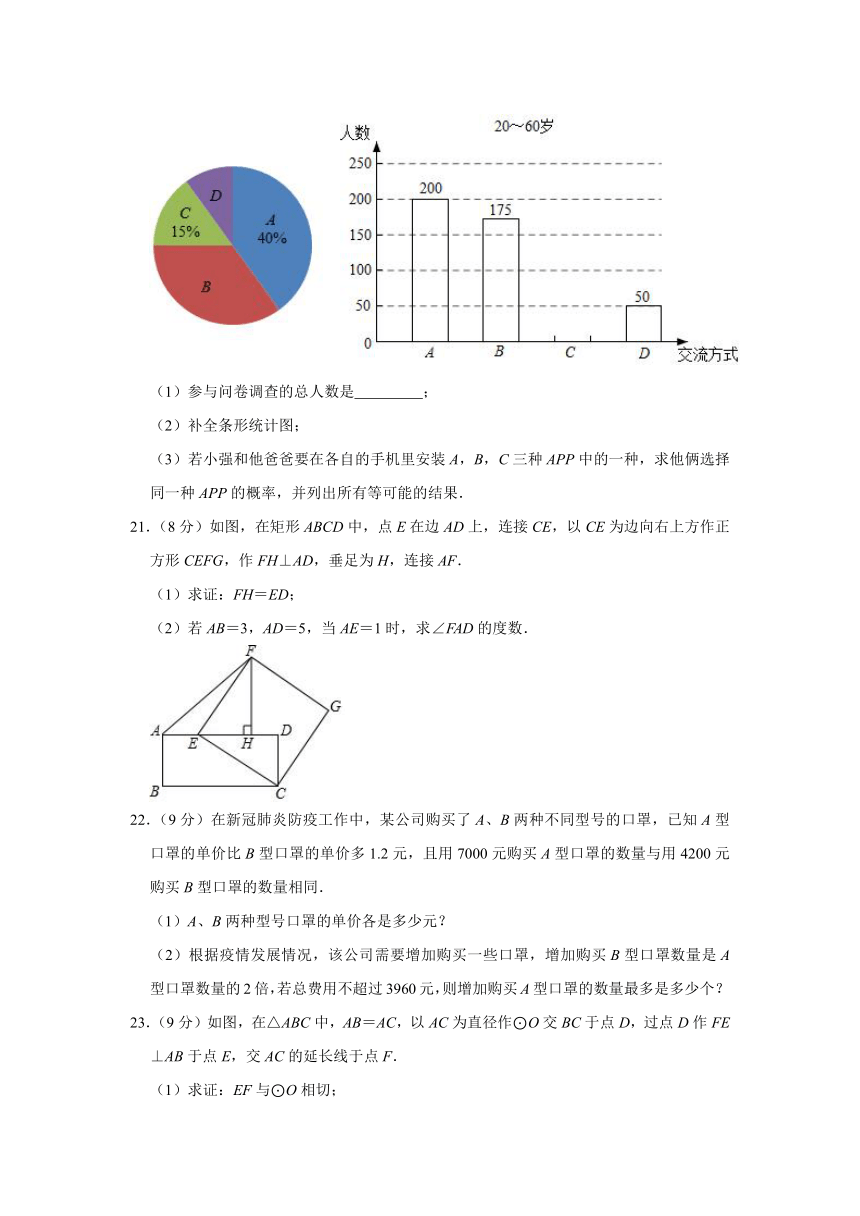
20.(8分)随着手机互联网技术的迅猛发展,越来越多的市民喜欢用手机APP进行沟通交流.某校数学兴趣小组为了解长沙某社区20~60岁居民最喜欢的手机APP沟通方式,针对给出的四种APP(A:微信、B:QQ、C:钉钉、D:其他)的使用情况,对社区内该年龄段的部分居民展开了随机问卷调查(每人必选且只能选择其中一项).根据调查结果绘制了如图不完整的统计图,请你根据图中信息解答下列问题:
(1)参与问卷调查的总人数是
;
(2)补全条形统计图;
(3)若小强和他爸爸要在各自的手机里安装A,B,C三种APP中的一种,求他俩选择同一种APP的概率,并列出所有等可能的结果.
21.(8分)如图,在矩形ABCD中,点E在边AD上,连接CE,以CE为边向右上方作正方形CEFG,作FH⊥AD,垂足为H,连接AF.
(1)求证:FH=ED;
(2)若AB=3,AD=5,当AE=1时,求∠FAD的度数.
22.(9分)在新冠肺炎防疫工作中,某公司购买了A、B两种不同型号的口罩,已知A型口罩的单价比B型口罩的单价多1.2元,且用7000元购买A型口罩的数量与用4200元购买B型口罩的数量相同.
(1)A、B两种型号口罩的单价各是多少元?
(2)根据疫情发展情况,该公司需要增加购买一些口罩,增加购买B型口罩数量是A型口罩数量的2倍,若总费用不超过3960元,则增加购买A型口罩的数量最多是多少个?
23.(9分)如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作FE⊥AB于点E,交AC的延长线于点F.
(1)求证:EF与⊙O相切;
(2)若,求.
24.(10分)我们约定:图象关于y轴对称的函数称为“Even函数”.例如:函数y=x2的图象关于y轴对称,则称函数y=x2是“Even函数”.
(1)下列函数是“Even函数”的有
(填序号);
①y=﹣x2+2020;
②y=2x+3;
③y=;
④y=2x2﹣5x.
(2)已知二次函数y=kx2+(k2﹣1)x+4(k为常数)是“Even函数”,与x轴交于A,B两点(A在B的左侧),顶点为M,点P是抛物线的对称轴上的一个动点.连接PB,求PM+PB的最小值.
(3)将(2)中“Even函数”图象进行平移得到新的二次函数y=ax2+bx+c(c≠0)的图象,其图象与y轴交于点C,与x轴交点A'、B'之间的距离为4,且以A'B'为直径的圆恰好经过点C,求a,b,c的值.
25.(10分)如图,已知抛物线y=x2+bx+c经过原点O,它与x轴的另一个交点记作点C,对称轴是直线x=2,点P在对称轴上,从抛物线上的点A出发,沿对称轴向上运动,运动时间为t秒,连接OP并延长交抛物线于点B.
(1)求抛物线的函数解析式;
(2)如图,连接OA,AC,当点B位于直线AC下方的抛物线上(不与点A,C重合)时,过点B作BD∥OA交AC于点D,求线段BD的最大值;
(3)连接AB,若点P的运动速度为每秒个单位,当△AOB为直角三角形时,求t的值.
2020-2021学年湖南省长沙市天心区九年级(下)期中数学试卷
参考答案与试题解析
一、选择题(本大题共12小题,每小题3分,共36分)
1.(3分)下列实数是无理数的是( )
A.0
B.
C.
D.
【分析】分别根据无理数、有理数的定义即可判定选择项.
【解答】解:A、0是整数,属于有理数,故本选项不合题意;
B、属于无理数,故本选项符合题意;
C、是分数,是有理数,故本选项不符合题意;
D、﹣=﹣4,是整数,属于有理数,故本选项不合题意;
故选:B.
2.(3分)下列图形中,既是轴对称图形又是中心对称图形的是( )
A.
B.
C.
D.
【分析】根据轴对称图形与中心对称图形的概念求解.
【解答】解:A、不是轴对称图形,也不是中心对称图形,故本选项错误;
B、不是轴对称图形,也不是中心对称图形,故本选项错误;
C、是轴对称图形,不是中心对称图形,故本选项错误;
D、是轴对称图形,也是中心对称图形,故本选项正确.
故选:D.
3.(3分)2021年2月27日,岳麓山多个地方人头攒动,当日麓山景区接待游客122700人次,高居全省各景区第一位,其中122700用科学记数法表示为( )
A.1.227×105
B.1.227×106
C.1.227×104
D.0.1227×107
【分析】用科学记数法表示较大的数时,一般形式为a×10n,其中1≤|a|<10,n为整数,且n比原来的整数位数少1,据此判断即可.
【解答】解:122700=1.227×105.
故选:A.
4.(3分)下列计算中,正确的是( )
A.(a2)3=a5
B.3a﹣2a=1
C.(3a)2=9a
D.a?a2=a3
【分析】分别根据幂的乘方运算法则,合并同类项法则,积的乘方运算法则以及同底数幂的乘法法则逐一判断即可.
【解答】解:A、(a2)3=a6,故本选项不合题意;
B、3a﹣2a=a,故本选项不合题意;
C、(3a)2=9a2,故本选项不合题意;
D、a?a2=a3,故本选项符合题意;
故选:D.
5.(3分)已知关于x的一元二次方程x2﹣4x+c=0有两个相等的实数根,则c=( )
A.4
B.2
C.1
D.﹣4
【分析】根据方程有两个相等的实数根结合根的判别式即可得出关于c的一元一次方程,解方程即可得出结论.
【解答】解:∵方程x2﹣4x+c=0有两个相等的实数根,
∴Δ=(﹣4)2﹣4×1×c=16﹣4c=0,
解得:c=4.
故选:A.
6.(3分)圆锥的底面圆的半径r=3,高h=4,则圆锥的侧面积是( )
A.10π
B.15π
C.30π
D.45π
【分析】先求圆锥的母线,再根据公式求侧面积.
【解答】解:由勾股定理得:母线l===5,
∴S侧=?2πr?l=πrl=π×3×5=15π.
故选:B.
7.(3分)不等式组的解在数轴上表示为( )
A.
B.
C.
D.
【分析】先解每一个不等式,再根据结果判断数轴表示的正确方法.
【解答】解:由不等式①,得2x>2,解得x>1,
由不等式②,得﹣2x≤﹣4,解得x≥2,
∴数轴表示的正确的是C选项,
故选:C.
8.(3分)如图,在直角坐标系中,点A是x轴正半轴上的一个定点,点B是双曲线(x>0)上的一个动点,当点B的横坐标逐渐增大时,△OAB的面积将会( )
A.逐渐增大
B.不变
C.逐渐减小
D.先增大后减小
【分析】过点B作BD⊥x轴于点D,由反比例函数的性质可知无论B点怎样变化△OBD的面积不变,当点B的横坐标逐渐增大时纵坐标减小,故△ABD的面积减小,所以△OAB的面积将会减小.
【解答】解:过点B作BD⊥x轴于点D,
∵B是双曲线y=上的点,
∴无论B点怎样变化△OBD的面积不变,
∵当点B的横坐标逐渐增大时纵坐标减小,
∴△ABD的面积减小,
∴△OAB的面积将会减小.
故选:C.
9.(3分)如图,AB∥CD,∠A=47°,∠C=28°,则∠AEC的大小应为( )
A.19°
B.29°
C.65°
D.75°
【分析】先根据平行线的性质可得出∠C=∠B=28°,再由外角定理即可得出答案.
【解答】解:∵AB∥CD,
∴∠C=∠B=28°,
∴∠AEC=∠A+∠B=28°+47°=75°.
故选:D.
10.(3分)如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为2,∠B=135°,则的长( )
A.2π
B.π
C.
D.
【分析】连接OA、OC,然后根据圆周角定理求得∠AOC的度数,最后根据弧长公式求解.
【解答】解:连接OA、OC,
∵∠B=135°,
∴∠D=180°﹣135°=45°,
∴∠AOC=90°,
则的长==π.
故选:B.
11.(3分)植树节这天有20名同学种了52棵树苗,其中男生每人种树3棵,女生每人种树2棵.设男生有x人,女生有y人,根据题意,下列方程组正确的是( )
A.
B.
C.
D.
【分析】设男生有x人,女生有y人,根据男女生人数为20,共种了52棵树苗,列出方程组成方程组即可.
【解答】解:设男生有x人,女生有y人,
根据题意可得:,
故选:A.
12.(3分)如图,在矩形ABCD中,AB=8,BC=12,E是AB边的中点,F是线段BC上的动点,将△EBF沿EF所在直线折叠得到△EB'F,连接B'D,则B'D的最小值是( )
A.8
B.12
C.
D.
【分析】由折叠可得,BE=B'E=AE,点B′在以E为圆心EA为半径的圆弧上运动.当D、B′、E共线时,B′D的长度最小.根据勾股定理求出DE,根据折叠的性质可知B′E=BE=4,即可求出B′D的最小值.
【解答】解:如图,B′的运动轨迹是以E为圆心EA为半径的圆弧,
∴当B′点落在DE上时,B′D取得最小值.
根据折叠的性质,可得△EBF≌△EB′F,
∴EB′⊥B′F,EB′=EB,
∵E是AB边的中点,AB=8,
∴AE=EB′=4,
∵AD=BC=12,
∴DE==4,
∴DB′=DE﹣B'E=﹣4.
故选:D.
二、填空题(本大题共4小题,每小题3分,共12分)
13.(3分)甲、乙两人进行射击测试,每人10次射击成绩的平均数都是9环,方差分别是:,,则射击成绩较稳定的是 甲 .(填“甲”或“乙”)
【分析】根据方差的定义,方差越小数据越稳定.
【解答】解:∵,,
∴S甲2<S乙2,
∴射击成绩较稳定的是甲;
故答案为:甲.
14.(3分)分解因式:2a3﹣8a= 2a(a+2)(a﹣2) .
【分析】原式提取2a,再利用平方差公式分解即可.
【解答】解:原式=2a(a2﹣4)=2a(a+2)(a﹣2),
故答案为:2a(a+2)(a﹣2)
15.(3分)在Rt△ABC中,AB是斜边,AB=10,BC=6,则cosA= .
【分析】根据勾股定理求出AC,根据余弦的定义计算,得到答案.
【解答】解:在Rt△ABC中,AB是斜边,AB=10,BC=6,
由勾股定理得,AC==8,
则cosA===,
故答案为:.
16.(3分)已知二次函数y=ax2+bx+c(a,b,c为整数且a≠0),对一切实数x恒有x≤y≤2x2+,则其解析式为 y=x2+x .
【分析】根据二次函数的性质、二次函数与一元二次方程的关系,通过变形,可以分别求出a、b、c的值,从而可以得到二次函数的解析式.
【解答】解:y=ax2+bx+c,对一切实数x恒有x≤y≤2x2+,
∴对一切实数x恒有x≤ax2+bx+c≤2x2+,
∴当x=0时,0≤c≤,
∵c为整数,
∴c=0,
∴x≤ax2+bx≤2x2+,
当ax2+bx≥x时,可得ax2+(b﹣1)x≥0,
∴,
解得b=1,
∴ax2+x≤2x2+,
∴(2﹣a)x2﹣x+≥0,
∴当a=2时,﹣x+≥0不是对于一切x成立,故不符合题意;
当a≠2时,,
解得a≤1,
又∵a>0且为整数,
∴a=1,
∴二次函数的解析式为y=x2+x,
故答案为:y=x2+x.
三、解答题(本大题共9小题,共72分,解答应写出必要文字说明、证明过程或演算步骤)
17.(6分)计算:.
【分析】首先计算零指数幂、负整数指数幂、特殊角的三角函数值和绝对值,然后计算乘法,最后从左向右依次计算,求出算式的值是多少即可.
【解答】解:
=﹣1﹣3+1﹣2×
=﹣3﹣
=﹣3.
18.(6分)先化简,再求值:(x﹣2y)2﹣x(x﹣4y),其中,x=1,y=﹣1.
【分析】根据整式的运算法则即可求出答案.
【解答】解:原式=x2﹣4xy+4y2﹣x2+4xy
=4y2,
当x=1,y=1时,
原式=4×1=4.
19.(6分)已知:如图,在△ABC中,∠C=90°.
(1)作图题:在AC边上,找一个点D,使点D到AB的距离等于DC,下列选项中,选出作法正确的 ② ;
①取AC的中点D;
②用尺规作角B的平分线,交AC于点D;
③用尺规作AB边的中垂线,交AC或其延长线于点D;
(2)在(1)的条件下,若AB=5,AC=4,求CD的长.
【分析】(1)利用角平分线的性质定理解决问题即可.
(2)过点D作DE⊥AB,垂足为E,利用勾股定理构建方程求解即可.
【解答】解:(1)作∠ABC的角平分线交AC于点D.
故答案为:②.
(2)过点D作DE⊥AB,垂足为E,
∵DE⊥AB
设CD=x,则DE=x,
在△ADE中:AD2=AE2+DE2,
即:(4﹣x)2=4+x2,
解得:,
∴CD的长为.
20.(8分)随着手机互联网技术的迅猛发展,越来越多的市民喜欢用手机APP进行沟通交流.某校数学兴趣小组为了解长沙某社区20~60岁居民最喜欢的手机APP沟通方式,针对给出的四种APP(A:微信、B:QQ、C:钉钉、D:其他)的使用情况,对社区内该年龄段的部分居民展开了随机问卷调查(每人必选且只能选择其中一项).根据调查结果绘制了如图不完整的统计图,请你根据图中信息解答下列问题:
(1)参与问卷调查的总人数是 500人 ;
(2)补全条形统计图;
(3)若小强和他爸爸要在各自的手机里安装A,B,C三种APP中的一种,求他俩选择同一种APP的概率,并列出所有等可能的结果.
【分析】(1)根据A的人数÷其所占的比例=参与问卷调查的总人数;
(2)求出C的人数,再将条形统计图补充完整即可;
(3)列表得出所有结果,再由概率公式求解即可.
【解答】解:(1)200÷40%=500(人),
即参与问卷调查的总人数为500人,
故答案为:500人;
(2)500×15%=75(人),
补全条形统计图如图所示:
(3)根据题意列表如下:
所有可能结果如下:AA,AB,AC,BA,BB,BC,CA,CB,CC共9种,
小强和爸爸选择同一种APP的可能结果有AA,BB,CC共3种,
∴小强和他爸爸选择同一种APP的概率为.
21.(8分)如图,在矩形ABCD中,点E在边AD上,连接CE,以CE为边向右上方作正方形CEFG,作FH⊥AD,垂足为H,连接AF.
(1)求证:FH=ED;
(2)若AB=3,AD=5,当AE=1时,求∠FAD的度数.
【分析】(1)根据正方形的性质,可得EF=CE,再根据∠CEF=∠90°,进而可得∠FEH=∠DCE,结合已知条件∠FHE=∠D=90°,利用“AAS”即可证明△FEH≌△ECD,由全等三角形的性质可得FH=ED;
(2)根据矩形的性质得到CD=AB=3,求得DE=4,根据全等三角形的性质得到FH=DE=4,EH=CD=3,得到AH=FH,根据等腰直角三角形的性质得到结论.
【解答】(1)证明:∵四边形CEFG是正方形,
∴CE=EF,
∵∠FEC=∠FEH+∠CED=90°,∠DCE+∠CED=90°,
∴∠FEH=∠DCE,
在△FEH和△ECD中,
∴△FEH≌△ECD(AAS),
∴FH=ED;
(2)解:∵在矩形ABCD中,AB=3,AD=5,
∴CD=AB=3,
∵AE=1,
∴DE=4,
∵△FEH≌△ECD,
∴FH=DE=4,EH=CD=3,
∴AH=4,
∴AH=FH,
∵∠FHE=90°,
∴∠FAD=45°.
22.(9分)在新冠肺炎防疫工作中,某公司购买了A、B两种不同型号的口罩,已知A型口罩的单价比B型口罩的单价多1.2元,且用7000元购买A型口罩的数量与用4200元购买B型口罩的数量相同.
(1)A、B两种型号口罩的单价各是多少元?
(2)根据疫情发展情况,该公司需要增加购买一些口罩,增加购买B型口罩数量是A型口罩数量的2倍,若总费用不超过3960元,则增加购买A型口罩的数量最多是多少个?
【分析】(1)设B型口罩的单价为x元,则A型口罩的单价为(x+1.2)元,根据“用7000元购买A型口罩的数量与用4200元购买B型口罩的数量相同”列出方程并解答;
(2)设增加购买A型口罩的数量是a个,根据“增加购买B型口罩数量是A型口罩数量的2倍,若总费用不超过3960元”列出不等式并解答.
【解答】解:(1)设B型口罩的单价为x元,则A型口罩的单价为(x+1.2)元,
根据题意,得:.
解方程,得:x=1.8.
经检验:x=1.8是原方程的根,且符合题意.
所以x+1.2=3.
答:A型口罩的单价为3元,则B型口罩的单价为1.8元;
(2)设增加购买A型口罩的数量是a个,则购买B型口罩的数量是2a个.
根据题意,得:3a+1.8×2a≤3960.
解不等式,得:a≤600.
答:增加购买A型口罩的数量最多是600个.
23.(9分)如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作FE⊥AB于点E,交AC的延长线于点F.
(1)求证:EF与⊙O相切;
(2)若,求.
【分析】(1)根据题意,作出合适的辅助线,利用等腰三角形的性质和平行线的性质,即可证明结论成立;
(2)根据题意和锐角三角函数、三角形相似,可以得到BE和AC的关系,然后即可得到的值.
【解答】证明:(1)连接OD,
∵AB=AC,
∴∠B=∠ACB,
又∵OC=OD,
∴∠ODC=∠ACB,
∴∠ODC=∠B,
∴OD∥AB,
∵EF⊥AB,
∴OD⊥EF,
又∵OD是圆的半径,
∴EF为⊙O的切线;
(2)∵tan∠CFD=,
∴tan∠CFD==,
设AE=3k,EF=4k,则AF=5k,
由(1)知OD∥AB,
∴△FOD∽△FAE,
∴,
∴,
∴3(5k﹣OA)=5OA,
解得OA=,
∴AB=AC=,
∴BE=AB﹣AE=﹣3k=k,
∴.
24.(10分)我们约定:图象关于y轴对称的函数称为“Even函数”.例如:函数y=x2的图象关于y轴对称,则称函数y=x2是“Even函数”.
(1)下列函数是“Even函数”的有 ①③ (填序号);
①y=﹣x2+2020;
②y=2x+3;
③y=;
④y=2x2﹣5x.
(2)已知二次函数y=kx2+(k2﹣1)x+4(k为常数)是“Even函数”,与x轴交于A,B两点(A在B的左侧),顶点为M,点P是抛物线的对称轴上的一个动点.连接PB,求PM+PB的最小值.
(3)将(2)中“Even函数”图象进行平移得到新的二次函数y=ax2+bx+c(c≠0)的图象,其图象与y轴交于点C,与x轴交点A'、B'之间的距离为4,且以A'B'为直径的圆恰好经过点C,求a,b,c的值.
【分析】(1)y=﹣x2+2020和y=的图象关于y轴对称;
(2)由题意先求出二次函数解析式为y=﹣x2+4,再求出,过点P作PG⊥AM于G,在Rt△PMG中,,所以PM+PB=PG+PB,过点B作BH⊥AM于点H,则PG+PB≥BH,线段BH的长就是PM+PB的最小值;
(3)由平移过程中a的值不变,则平移得到新的二次函数为y=﹣x2+bx+c,设A'(x1,0),B'(x2,0)(x1<x2),由根与系数关系可知:x1+x2=b,x1x2=﹣c,AB=4,可得b2+4c=16,圆心为F(,0),则()2+c2=4,得b2+4c2=16,联立方程组,即可求b、c的值.
【解答】解:(1)①y=﹣x2+2020对称轴为y轴,是“Even函数”,
②y=2x+3图象是直线,不是“Even函数”,
③y=图象关于y轴对称,是“Even函数”,
④y=2x2﹣5x=2(x﹣)2﹣,对称轴为直线x=,不是“Even函数”,
∴①③关于y轴对称,是“Even函数”,
故答案为①③;
(2)如图1,
∵二次函数y=kx2+(k2﹣1)x+4(k为常数)是“Even函数”,
∴,
解得:k=﹣1,
∴二次函数解析式为y=﹣x2+4,
据图形的对称性可知∠AMO=∠BMO,AM=BM=2,
∴,
过点P作PG⊥AM于G,
∴在Rt△PMG中,,
∴PM+PB=PG+PB,
过点B作BH⊥AM于点H,则PG+PB≥BH,
∴线段BH的长就是PM+PB的最小值,
∵=8,
又∵,
∴,即
,
∴PM+PB的最小值为;
(3)如图2,
∵平移抛物线时,开口方向和形状都不变,即a的值不变,
∴平移得到新的二次函数为y=﹣x2+bx+c,
由题意知,新函数的图象与x轴交于A',B'两点(A'在B'的左侧),与y轴交于点C,
设A'(x1,0),B'(x2,0)(x1<x2),
令x=0,得y=c,
∴C(0,c),
∵A'B'=4,
∴x2﹣x1=4,
由根与系数关系可知:x1+x2=b,x1x2=﹣c,
∵(x1+x2)2﹣4x1x2=(x2﹣x1)2,
∴b2+4c=42,即b2+4c=16,
∵以A'B'为直径的圆恰好经过点C,
∴该圆的圆心为F(,0),即F(,0),
∴CF=2,即()2+c2=4,
整理,得:b2+4c2=16,
联立方程组,
∵c≠0,
∴解得:,;
∴或.
25.(10分)如图,已知抛物线y=x2+bx+c经过原点O,它与x轴的另一个交点记作点C,对称轴是直线x=2,点P在对称轴上,从抛物线上的点A出发,沿对称轴向上运动,运动时间为t秒,连接OP并延长交抛物线于点B.
(1)求抛物线的函数解析式;
(2)如图,连接OA,AC,当点B位于直线AC下方的抛物线上(不与点A,C重合)时,过点B作BD∥OA交AC于点D,求线段BD的最大值;
(3)连接AB,若点P的运动速度为每秒个单位,当△AOB为直角三角形时,求t的值.
【分析】(1)由已知可得c=0,,即可求解析式;
(2)设直线AC与y轴交于点H,过点B作BE∥y轴交AC于点E,先证明△OHA∽△BED,再求出直线AC的解析式为y=2x﹣8,分别求出OH=8,OA=2,则可求BD=,设点B(a,a2﹣4a),则点E(a,2a﹣8),所以BE=﹣(a﹣3)2+1,当a=3时,BE取最大值1,此时
BD取最大值;
(3)分三种情况讨论:①若OB2=OA2+AB2,可求直线OB解析式为,P(2,﹣3),所以;②若AB2=OA2+OB2,可求直线OB解析式为,P(2,1),所以;③若OA2=AB2+OB2,可求直线OB解析式为y=﹣x,P(2,﹣2),所以;
【解答】解:(1)∵抛物线y=x2+bx+c经过原点O,且对称轴是直线x=2,
∴c=0,,
∴b=﹣4,c=0,
∴抛物线解析式为y=x2﹣4x;
(2)设直线AC与y轴交于点H,过点B作BE∥y轴交AC于点E,
∴∠OHA=∠BED,
∵OA∥BD,
∴∠OAD=∠BDA,
∴∠OAH=∠BDE,
∴△OHA∽△BED,
∴,
由点A(2,﹣4),点C(4,0),
设直线AC的解析式为y=kx+b,
∴,
∴,
∴直线AC的解析式为y=2x﹣8
∴点H(0,8),
∴OH=8,
又∵OA=,
∴,
∴BD=,
设点B(a,a2﹣4a),则点E(a,2a﹣8),
∴BE=(2a﹣8)﹣(a2﹣4a)=﹣a2+6a﹣8=﹣(a﹣3)2+1,
当a=3时,BE取最大值1,此时
BD取最大值;
(3)∵y=x2﹣4x=(x﹣2)2﹣4,
∴点A(2,﹣4),
又∵点B(a,a2﹣4a),
∴OA2=22+42=20,OB2=a2+(a2﹣4a)2,AB2=(a﹣2)2+(a2﹣4a+4)2,
①若OB2=OA2+AB2,则a2+(a2﹣4a)2=20+(a﹣2)2+(a2﹣4a+4)2,
解得a=2(舍)或,
∴,,
∴直线OB解析式为,
当x=2时,y=﹣3,即P(2,﹣3),
∴;
②若AB2=OA2+OB2,则(a﹣2)2+(a2﹣4a+4)2=20+a2+(a2﹣4a)2,
解得a=0(舍)或,
∴,,
∴直线OB解析式为,
当x=2时,y=1,即P(2,1),
∴;
③若OA2=AB2+OB2,则20=(a﹣2)2+(a2﹣4a+4)2+a2+(a2﹣4a)2,
整理,得:a3﹣8a2+21a﹣18=0,
∴a3﹣3a2﹣5a2+15a+6a﹣18
=a2(a﹣3)﹣5a(a﹣3)+6(a﹣3)
=(a﹣3)(a2﹣5a+6)
=(a﹣3)2(a﹣2)
=0,
∴a=3或a=2(舍),
∴B(3,﹣3),
∴直线OB解析式为y=﹣x,
当x=2时,y=﹣2,即P(2,﹣2),
∴;
综上所述,当△AOB为直角三角形时,t的值为2或4或10.
一、选择题(本大题共12小题,每小题3分,共36分)
1.(3分)下列实数是无理数的是( )
A.0
B.
C.
D.
2.(3分)下列图形中,既是轴对称图形又是中心对称图形的是( )
A.
B.
C.
D.
3.(3分)2021年2月27日,岳麓山多个地方人头攒动,当日麓山景区接待游客122700人次,高居全省各景区第一位,其中122700用科学记数法表示为( )
A.1.227×105
B.1.227×106
C.1.227×104
D.0.1227×107
4.(3分)下列计算中,正确的是( )
A.(a2)3=a5
B.3a﹣2a=1
C.(3a)2=9a
D.a?a2=a3
5.(3分)已知关于x的一元二次方程x2﹣4x+c=0有两个相等的实数根,则c=( )
A.4
B.2
C.1
D.﹣4
6.(3分)圆锥的底面圆的半径r=3,高h=4,则圆锥的侧面积是( )
A.10π
B.15π
C.30π
D.45π
7.(3分)不等式组的解在数轴上表示为( )
A.
B.
C.
D.
8.(3分)如图,在直角坐标系中,点A是x轴正半轴上的一个定点,点B是双曲线(x>0)上的一个动点,当点B的横坐标逐渐增大时,△OAB的面积将会( )
A.逐渐增大
B.不变
C.逐渐减小
D.先增大后减小
9.(3分)如图,AB∥CD,∠A=47°,∠C=28°,则∠AEC的大小应为( )
A.19°
B.29°
C.65°
D.75°
10.(3分)如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为2,∠B=135°,则的长( )
A.2π
B.π
C.
D.
11.(3分)植树节这天有20名同学种了52棵树苗,其中男生每人种树3棵,女生每人种树2棵.设男生有x人,女生有y人,根据题意,下列方程组正确的是( )
A.
B.
C.
D.
12.(3分)如图,在矩形ABCD中,AB=8,BC=12,E是AB边的中点,F是线段BC上的动点,将△EBF沿EF所在直线折叠得到△EB'F,连接B'D,则B'D的最小值是( )
A.8
B.12
C.
D.
二、填空题(本大题共4小题,每小题3分,共12分)
13.(3分)甲、乙两人进行射击测试,每人10次射击成绩的平均数都是9环,方差分别是:,,则射击成绩较稳定的是
.(填“甲”或“乙”)
14.(3分)分解因式:2a3﹣8a=
.
15.(3分)在Rt△ABC中,AB是斜边,AB=10,BC=6,则cosA=
.
16.(3分)已知二次函数y=ax2+bx+c(a,b,c为整数且a≠0),对一切实数x恒有x≤y≤2x2+,则其解析式为
.
三、解答题(本大题共9小题,共72分,解答应写出必要文字说明、证明过程或演算步骤)
17.(6分)计算:.
18.(6分)先化简,再求值:(x﹣2y)2﹣x(x﹣4y),其中,x=1,y=﹣1.
19.(6分)已知:如图,在△ABC中,∠C=90°.
(1)作图题:在AC边上,找一个点D,使点D到AB的距离等于DC,下列选项中,选出作法正确的
;
①取AC的中点D;
②用尺规作角B的平分线,交AC于点D;
③用尺规作AB边的中垂线,交AC或其延长线于点D;
(2)在(1)的条件下,若AB=5,AC=4,求CD的长.
20.(8分)随着手机互联网技术的迅猛发展,越来越多的市民喜欢用手机APP进行沟通交流.某校数学兴趣小组为了解长沙某社区20~60岁居民最喜欢的手机APP沟通方式,针对给出的四种APP(A:微信、B:QQ、C:钉钉、D:其他)的使用情况,对社区内该年龄段的部分居民展开了随机问卷调查(每人必选且只能选择其中一项).根据调查结果绘制了如图不完整的统计图,请你根据图中信息解答下列问题:
(1)参与问卷调查的总人数是
;
(2)补全条形统计图;
(3)若小强和他爸爸要在各自的手机里安装A,B,C三种APP中的一种,求他俩选择同一种APP的概率,并列出所有等可能的结果.
21.(8分)如图,在矩形ABCD中,点E在边AD上,连接CE,以CE为边向右上方作正方形CEFG,作FH⊥AD,垂足为H,连接AF.
(1)求证:FH=ED;
(2)若AB=3,AD=5,当AE=1时,求∠FAD的度数.
22.(9分)在新冠肺炎防疫工作中,某公司购买了A、B两种不同型号的口罩,已知A型口罩的单价比B型口罩的单价多1.2元,且用7000元购买A型口罩的数量与用4200元购买B型口罩的数量相同.
(1)A、B两种型号口罩的单价各是多少元?
(2)根据疫情发展情况,该公司需要增加购买一些口罩,增加购买B型口罩数量是A型口罩数量的2倍,若总费用不超过3960元,则增加购买A型口罩的数量最多是多少个?
23.(9分)如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作FE⊥AB于点E,交AC的延长线于点F.
(1)求证:EF与⊙O相切;
(2)若,求.
24.(10分)我们约定:图象关于y轴对称的函数称为“Even函数”.例如:函数y=x2的图象关于y轴对称,则称函数y=x2是“Even函数”.
(1)下列函数是“Even函数”的有
(填序号);
①y=﹣x2+2020;
②y=2x+3;
③y=;
④y=2x2﹣5x.
(2)已知二次函数y=kx2+(k2﹣1)x+4(k为常数)是“Even函数”,与x轴交于A,B两点(A在B的左侧),顶点为M,点P是抛物线的对称轴上的一个动点.连接PB,求PM+PB的最小值.
(3)将(2)中“Even函数”图象进行平移得到新的二次函数y=ax2+bx+c(c≠0)的图象,其图象与y轴交于点C,与x轴交点A'、B'之间的距离为4,且以A'B'为直径的圆恰好经过点C,求a,b,c的值.
25.(10分)如图,已知抛物线y=x2+bx+c经过原点O,它与x轴的另一个交点记作点C,对称轴是直线x=2,点P在对称轴上,从抛物线上的点A出发,沿对称轴向上运动,运动时间为t秒,连接OP并延长交抛物线于点B.
(1)求抛物线的函数解析式;
(2)如图,连接OA,AC,当点B位于直线AC下方的抛物线上(不与点A,C重合)时,过点B作BD∥OA交AC于点D,求线段BD的最大值;
(3)连接AB,若点P的运动速度为每秒个单位,当△AOB为直角三角形时,求t的值.
2020-2021学年湖南省长沙市天心区九年级(下)期中数学试卷
参考答案与试题解析
一、选择题(本大题共12小题,每小题3分,共36分)
1.(3分)下列实数是无理数的是( )
A.0
B.
C.
D.
【分析】分别根据无理数、有理数的定义即可判定选择项.
【解答】解:A、0是整数,属于有理数,故本选项不合题意;
B、属于无理数,故本选项符合题意;
C、是分数,是有理数,故本选项不符合题意;
D、﹣=﹣4,是整数,属于有理数,故本选项不合题意;
故选:B.
2.(3分)下列图形中,既是轴对称图形又是中心对称图形的是( )
A.
B.
C.
D.
【分析】根据轴对称图形与中心对称图形的概念求解.
【解答】解:A、不是轴对称图形,也不是中心对称图形,故本选项错误;
B、不是轴对称图形,也不是中心对称图形,故本选项错误;
C、是轴对称图形,不是中心对称图形,故本选项错误;
D、是轴对称图形,也是中心对称图形,故本选项正确.
故选:D.
3.(3分)2021年2月27日,岳麓山多个地方人头攒动,当日麓山景区接待游客122700人次,高居全省各景区第一位,其中122700用科学记数法表示为( )
A.1.227×105
B.1.227×106
C.1.227×104
D.0.1227×107
【分析】用科学记数法表示较大的数时,一般形式为a×10n,其中1≤|a|<10,n为整数,且n比原来的整数位数少1,据此判断即可.
【解答】解:122700=1.227×105.
故选:A.
4.(3分)下列计算中,正确的是( )
A.(a2)3=a5
B.3a﹣2a=1
C.(3a)2=9a
D.a?a2=a3
【分析】分别根据幂的乘方运算法则,合并同类项法则,积的乘方运算法则以及同底数幂的乘法法则逐一判断即可.
【解答】解:A、(a2)3=a6,故本选项不合题意;
B、3a﹣2a=a,故本选项不合题意;
C、(3a)2=9a2,故本选项不合题意;
D、a?a2=a3,故本选项符合题意;
故选:D.
5.(3分)已知关于x的一元二次方程x2﹣4x+c=0有两个相等的实数根,则c=( )
A.4
B.2
C.1
D.﹣4
【分析】根据方程有两个相等的实数根结合根的判别式即可得出关于c的一元一次方程,解方程即可得出结论.
【解答】解:∵方程x2﹣4x+c=0有两个相等的实数根,
∴Δ=(﹣4)2﹣4×1×c=16﹣4c=0,
解得:c=4.
故选:A.
6.(3分)圆锥的底面圆的半径r=3,高h=4,则圆锥的侧面积是( )
A.10π
B.15π
C.30π
D.45π
【分析】先求圆锥的母线,再根据公式求侧面积.
【解答】解:由勾股定理得:母线l===5,
∴S侧=?2πr?l=πrl=π×3×5=15π.
故选:B.
7.(3分)不等式组的解在数轴上表示为( )
A.
B.
C.
D.
【分析】先解每一个不等式,再根据结果判断数轴表示的正确方法.
【解答】解:由不等式①,得2x>2,解得x>1,
由不等式②,得﹣2x≤﹣4,解得x≥2,
∴数轴表示的正确的是C选项,
故选:C.
8.(3分)如图,在直角坐标系中,点A是x轴正半轴上的一个定点,点B是双曲线(x>0)上的一个动点,当点B的横坐标逐渐增大时,△OAB的面积将会( )
A.逐渐增大
B.不变
C.逐渐减小
D.先增大后减小
【分析】过点B作BD⊥x轴于点D,由反比例函数的性质可知无论B点怎样变化△OBD的面积不变,当点B的横坐标逐渐增大时纵坐标减小,故△ABD的面积减小,所以△OAB的面积将会减小.
【解答】解:过点B作BD⊥x轴于点D,
∵B是双曲线y=上的点,
∴无论B点怎样变化△OBD的面积不变,
∵当点B的横坐标逐渐增大时纵坐标减小,
∴△ABD的面积减小,
∴△OAB的面积将会减小.
故选:C.
9.(3分)如图,AB∥CD,∠A=47°,∠C=28°,则∠AEC的大小应为( )
A.19°
B.29°
C.65°
D.75°
【分析】先根据平行线的性质可得出∠C=∠B=28°,再由外角定理即可得出答案.
【解答】解:∵AB∥CD,
∴∠C=∠B=28°,
∴∠AEC=∠A+∠B=28°+47°=75°.
故选:D.
10.(3分)如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为2,∠B=135°,则的长( )
A.2π
B.π
C.
D.
【分析】连接OA、OC,然后根据圆周角定理求得∠AOC的度数,最后根据弧长公式求解.
【解答】解:连接OA、OC,
∵∠B=135°,
∴∠D=180°﹣135°=45°,
∴∠AOC=90°,
则的长==π.
故选:B.
11.(3分)植树节这天有20名同学种了52棵树苗,其中男生每人种树3棵,女生每人种树2棵.设男生有x人,女生有y人,根据题意,下列方程组正确的是( )
A.
B.
C.
D.
【分析】设男生有x人,女生有y人,根据男女生人数为20,共种了52棵树苗,列出方程组成方程组即可.
【解答】解:设男生有x人,女生有y人,
根据题意可得:,
故选:A.
12.(3分)如图,在矩形ABCD中,AB=8,BC=12,E是AB边的中点,F是线段BC上的动点,将△EBF沿EF所在直线折叠得到△EB'F,连接B'D,则B'D的最小值是( )
A.8
B.12
C.
D.
【分析】由折叠可得,BE=B'E=AE,点B′在以E为圆心EA为半径的圆弧上运动.当D、B′、E共线时,B′D的长度最小.根据勾股定理求出DE,根据折叠的性质可知B′E=BE=4,即可求出B′D的最小值.
【解答】解:如图,B′的运动轨迹是以E为圆心EA为半径的圆弧,
∴当B′点落在DE上时,B′D取得最小值.
根据折叠的性质,可得△EBF≌△EB′F,
∴EB′⊥B′F,EB′=EB,
∵E是AB边的中点,AB=8,
∴AE=EB′=4,
∵AD=BC=12,
∴DE==4,
∴DB′=DE﹣B'E=﹣4.
故选:D.
二、填空题(本大题共4小题,每小题3分,共12分)
13.(3分)甲、乙两人进行射击测试,每人10次射击成绩的平均数都是9环,方差分别是:,,则射击成绩较稳定的是 甲 .(填“甲”或“乙”)
【分析】根据方差的定义,方差越小数据越稳定.
【解答】解:∵,,
∴S甲2<S乙2,
∴射击成绩较稳定的是甲;
故答案为:甲.
14.(3分)分解因式:2a3﹣8a= 2a(a+2)(a﹣2) .
【分析】原式提取2a,再利用平方差公式分解即可.
【解答】解:原式=2a(a2﹣4)=2a(a+2)(a﹣2),
故答案为:2a(a+2)(a﹣2)
15.(3分)在Rt△ABC中,AB是斜边,AB=10,BC=6,则cosA= .
【分析】根据勾股定理求出AC,根据余弦的定义计算,得到答案.
【解答】解:在Rt△ABC中,AB是斜边,AB=10,BC=6,
由勾股定理得,AC==8,
则cosA===,
故答案为:.
16.(3分)已知二次函数y=ax2+bx+c(a,b,c为整数且a≠0),对一切实数x恒有x≤y≤2x2+,则其解析式为 y=x2+x .
【分析】根据二次函数的性质、二次函数与一元二次方程的关系,通过变形,可以分别求出a、b、c的值,从而可以得到二次函数的解析式.
【解答】解:y=ax2+bx+c,对一切实数x恒有x≤y≤2x2+,
∴对一切实数x恒有x≤ax2+bx+c≤2x2+,
∴当x=0时,0≤c≤,
∵c为整数,
∴c=0,
∴x≤ax2+bx≤2x2+,
当ax2+bx≥x时,可得ax2+(b﹣1)x≥0,
∴,
解得b=1,
∴ax2+x≤2x2+,
∴(2﹣a)x2﹣x+≥0,
∴当a=2时,﹣x+≥0不是对于一切x成立,故不符合题意;
当a≠2时,,
解得a≤1,
又∵a>0且为整数,
∴a=1,
∴二次函数的解析式为y=x2+x,
故答案为:y=x2+x.
三、解答题(本大题共9小题,共72分,解答应写出必要文字说明、证明过程或演算步骤)
17.(6分)计算:.
【分析】首先计算零指数幂、负整数指数幂、特殊角的三角函数值和绝对值,然后计算乘法,最后从左向右依次计算,求出算式的值是多少即可.
【解答】解:
=﹣1﹣3+1﹣2×
=﹣3﹣
=﹣3.
18.(6分)先化简,再求值:(x﹣2y)2﹣x(x﹣4y),其中,x=1,y=﹣1.
【分析】根据整式的运算法则即可求出答案.
【解答】解:原式=x2﹣4xy+4y2﹣x2+4xy
=4y2,
当x=1,y=1时,
原式=4×1=4.
19.(6分)已知:如图,在△ABC中,∠C=90°.
(1)作图题:在AC边上,找一个点D,使点D到AB的距离等于DC,下列选项中,选出作法正确的 ② ;
①取AC的中点D;
②用尺规作角B的平分线,交AC于点D;
③用尺规作AB边的中垂线,交AC或其延长线于点D;
(2)在(1)的条件下,若AB=5,AC=4,求CD的长.
【分析】(1)利用角平分线的性质定理解决问题即可.
(2)过点D作DE⊥AB,垂足为E,利用勾股定理构建方程求解即可.
【解答】解:(1)作∠ABC的角平分线交AC于点D.
故答案为:②.
(2)过点D作DE⊥AB,垂足为E,
∵DE⊥AB
设CD=x,则DE=x,
在△ADE中:AD2=AE2+DE2,
即:(4﹣x)2=4+x2,
解得:,
∴CD的长为.
20.(8分)随着手机互联网技术的迅猛发展,越来越多的市民喜欢用手机APP进行沟通交流.某校数学兴趣小组为了解长沙某社区20~60岁居民最喜欢的手机APP沟通方式,针对给出的四种APP(A:微信、B:QQ、C:钉钉、D:其他)的使用情况,对社区内该年龄段的部分居民展开了随机问卷调查(每人必选且只能选择其中一项).根据调查结果绘制了如图不完整的统计图,请你根据图中信息解答下列问题:
(1)参与问卷调查的总人数是 500人 ;
(2)补全条形统计图;
(3)若小强和他爸爸要在各自的手机里安装A,B,C三种APP中的一种,求他俩选择同一种APP的概率,并列出所有等可能的结果.
【分析】(1)根据A的人数÷其所占的比例=参与问卷调查的总人数;
(2)求出C的人数,再将条形统计图补充完整即可;
(3)列表得出所有结果,再由概率公式求解即可.
【解答】解:(1)200÷40%=500(人),
即参与问卷调查的总人数为500人,
故答案为:500人;
(2)500×15%=75(人),
补全条形统计图如图所示:
(3)根据题意列表如下:
所有可能结果如下:AA,AB,AC,BA,BB,BC,CA,CB,CC共9种,
小强和爸爸选择同一种APP的可能结果有AA,BB,CC共3种,
∴小强和他爸爸选择同一种APP的概率为.
21.(8分)如图,在矩形ABCD中,点E在边AD上,连接CE,以CE为边向右上方作正方形CEFG,作FH⊥AD,垂足为H,连接AF.
(1)求证:FH=ED;
(2)若AB=3,AD=5,当AE=1时,求∠FAD的度数.
【分析】(1)根据正方形的性质,可得EF=CE,再根据∠CEF=∠90°,进而可得∠FEH=∠DCE,结合已知条件∠FHE=∠D=90°,利用“AAS”即可证明△FEH≌△ECD,由全等三角形的性质可得FH=ED;
(2)根据矩形的性质得到CD=AB=3,求得DE=4,根据全等三角形的性质得到FH=DE=4,EH=CD=3,得到AH=FH,根据等腰直角三角形的性质得到结论.
【解答】(1)证明:∵四边形CEFG是正方形,
∴CE=EF,
∵∠FEC=∠FEH+∠CED=90°,∠DCE+∠CED=90°,
∴∠FEH=∠DCE,
在△FEH和△ECD中,
∴△FEH≌△ECD(AAS),
∴FH=ED;
(2)解:∵在矩形ABCD中,AB=3,AD=5,
∴CD=AB=3,
∵AE=1,
∴DE=4,
∵△FEH≌△ECD,
∴FH=DE=4,EH=CD=3,
∴AH=4,
∴AH=FH,
∵∠FHE=90°,
∴∠FAD=45°.
22.(9分)在新冠肺炎防疫工作中,某公司购买了A、B两种不同型号的口罩,已知A型口罩的单价比B型口罩的单价多1.2元,且用7000元购买A型口罩的数量与用4200元购买B型口罩的数量相同.
(1)A、B两种型号口罩的单价各是多少元?
(2)根据疫情发展情况,该公司需要增加购买一些口罩,增加购买B型口罩数量是A型口罩数量的2倍,若总费用不超过3960元,则增加购买A型口罩的数量最多是多少个?
【分析】(1)设B型口罩的单价为x元,则A型口罩的单价为(x+1.2)元,根据“用7000元购买A型口罩的数量与用4200元购买B型口罩的数量相同”列出方程并解答;
(2)设增加购买A型口罩的数量是a个,根据“增加购买B型口罩数量是A型口罩数量的2倍,若总费用不超过3960元”列出不等式并解答.
【解答】解:(1)设B型口罩的单价为x元,则A型口罩的单价为(x+1.2)元,
根据题意,得:.
解方程,得:x=1.8.
经检验:x=1.8是原方程的根,且符合题意.
所以x+1.2=3.
答:A型口罩的单价为3元,则B型口罩的单价为1.8元;
(2)设增加购买A型口罩的数量是a个,则购买B型口罩的数量是2a个.
根据题意,得:3a+1.8×2a≤3960.
解不等式,得:a≤600.
答:增加购买A型口罩的数量最多是600个.
23.(9分)如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作FE⊥AB于点E,交AC的延长线于点F.
(1)求证:EF与⊙O相切;
(2)若,求.
【分析】(1)根据题意,作出合适的辅助线,利用等腰三角形的性质和平行线的性质,即可证明结论成立;
(2)根据题意和锐角三角函数、三角形相似,可以得到BE和AC的关系,然后即可得到的值.
【解答】证明:(1)连接OD,
∵AB=AC,
∴∠B=∠ACB,
又∵OC=OD,
∴∠ODC=∠ACB,
∴∠ODC=∠B,
∴OD∥AB,
∵EF⊥AB,
∴OD⊥EF,
又∵OD是圆的半径,
∴EF为⊙O的切线;
(2)∵tan∠CFD=,
∴tan∠CFD==,
设AE=3k,EF=4k,则AF=5k,
由(1)知OD∥AB,
∴△FOD∽△FAE,
∴,
∴,
∴3(5k﹣OA)=5OA,
解得OA=,
∴AB=AC=,
∴BE=AB﹣AE=﹣3k=k,
∴.
24.(10分)我们约定:图象关于y轴对称的函数称为“Even函数”.例如:函数y=x2的图象关于y轴对称,则称函数y=x2是“Even函数”.
(1)下列函数是“Even函数”的有 ①③ (填序号);
①y=﹣x2+2020;
②y=2x+3;
③y=;
④y=2x2﹣5x.
(2)已知二次函数y=kx2+(k2﹣1)x+4(k为常数)是“Even函数”,与x轴交于A,B两点(A在B的左侧),顶点为M,点P是抛物线的对称轴上的一个动点.连接PB,求PM+PB的最小值.
(3)将(2)中“Even函数”图象进行平移得到新的二次函数y=ax2+bx+c(c≠0)的图象,其图象与y轴交于点C,与x轴交点A'、B'之间的距离为4,且以A'B'为直径的圆恰好经过点C,求a,b,c的值.
【分析】(1)y=﹣x2+2020和y=的图象关于y轴对称;
(2)由题意先求出二次函数解析式为y=﹣x2+4,再求出,过点P作PG⊥AM于G,在Rt△PMG中,,所以PM+PB=PG+PB,过点B作BH⊥AM于点H,则PG+PB≥BH,线段BH的长就是PM+PB的最小值;
(3)由平移过程中a的值不变,则平移得到新的二次函数为y=﹣x2+bx+c,设A'(x1,0),B'(x2,0)(x1<x2),由根与系数关系可知:x1+x2=b,x1x2=﹣c,AB=4,可得b2+4c=16,圆心为F(,0),则()2+c2=4,得b2+4c2=16,联立方程组,即可求b、c的值.
【解答】解:(1)①y=﹣x2+2020对称轴为y轴,是“Even函数”,
②y=2x+3图象是直线,不是“Even函数”,
③y=图象关于y轴对称,是“Even函数”,
④y=2x2﹣5x=2(x﹣)2﹣,对称轴为直线x=,不是“Even函数”,
∴①③关于y轴对称,是“Even函数”,
故答案为①③;
(2)如图1,
∵二次函数y=kx2+(k2﹣1)x+4(k为常数)是“Even函数”,
∴,
解得:k=﹣1,
∴二次函数解析式为y=﹣x2+4,
据图形的对称性可知∠AMO=∠BMO,AM=BM=2,
∴,
过点P作PG⊥AM于G,
∴在Rt△PMG中,,
∴PM+PB=PG+PB,
过点B作BH⊥AM于点H,则PG+PB≥BH,
∴线段BH的长就是PM+PB的最小值,
∵=8,
又∵,
∴,即
,
∴PM+PB的最小值为;
(3)如图2,
∵平移抛物线时,开口方向和形状都不变,即a的值不变,
∴平移得到新的二次函数为y=﹣x2+bx+c,
由题意知,新函数的图象与x轴交于A',B'两点(A'在B'的左侧),与y轴交于点C,
设A'(x1,0),B'(x2,0)(x1<x2),
令x=0,得y=c,
∴C(0,c),
∵A'B'=4,
∴x2﹣x1=4,
由根与系数关系可知:x1+x2=b,x1x2=﹣c,
∵(x1+x2)2﹣4x1x2=(x2﹣x1)2,
∴b2+4c=42,即b2+4c=16,
∵以A'B'为直径的圆恰好经过点C,
∴该圆的圆心为F(,0),即F(,0),
∴CF=2,即()2+c2=4,
整理,得:b2+4c2=16,
联立方程组,
∵c≠0,
∴解得:,;
∴或.
25.(10分)如图,已知抛物线y=x2+bx+c经过原点O,它与x轴的另一个交点记作点C,对称轴是直线x=2,点P在对称轴上,从抛物线上的点A出发,沿对称轴向上运动,运动时间为t秒,连接OP并延长交抛物线于点B.
(1)求抛物线的函数解析式;
(2)如图,连接OA,AC,当点B位于直线AC下方的抛物线上(不与点A,C重合)时,过点B作BD∥OA交AC于点D,求线段BD的最大值;
(3)连接AB,若点P的运动速度为每秒个单位,当△AOB为直角三角形时,求t的值.
【分析】(1)由已知可得c=0,,即可求解析式;
(2)设直线AC与y轴交于点H,过点B作BE∥y轴交AC于点E,先证明△OHA∽△BED,再求出直线AC的解析式为y=2x﹣8,分别求出OH=8,OA=2,则可求BD=,设点B(a,a2﹣4a),则点E(a,2a﹣8),所以BE=﹣(a﹣3)2+1,当a=3时,BE取最大值1,此时
BD取最大值;
(3)分三种情况讨论:①若OB2=OA2+AB2,可求直线OB解析式为,P(2,﹣3),所以;②若AB2=OA2+OB2,可求直线OB解析式为,P(2,1),所以;③若OA2=AB2+OB2,可求直线OB解析式为y=﹣x,P(2,﹣2),所以;
【解答】解:(1)∵抛物线y=x2+bx+c经过原点O,且对称轴是直线x=2,
∴c=0,,
∴b=﹣4,c=0,
∴抛物线解析式为y=x2﹣4x;
(2)设直线AC与y轴交于点H,过点B作BE∥y轴交AC于点E,
∴∠OHA=∠BED,
∵OA∥BD,
∴∠OAD=∠BDA,
∴∠OAH=∠BDE,
∴△OHA∽△BED,
∴,
由点A(2,﹣4),点C(4,0),
设直线AC的解析式为y=kx+b,
∴,
∴,
∴直线AC的解析式为y=2x﹣8
∴点H(0,8),
∴OH=8,
又∵OA=,
∴,
∴BD=,
设点B(a,a2﹣4a),则点E(a,2a﹣8),
∴BE=(2a﹣8)﹣(a2﹣4a)=﹣a2+6a﹣8=﹣(a﹣3)2+1,
当a=3时,BE取最大值1,此时
BD取最大值;
(3)∵y=x2﹣4x=(x﹣2)2﹣4,
∴点A(2,﹣4),
又∵点B(a,a2﹣4a),
∴OA2=22+42=20,OB2=a2+(a2﹣4a)2,AB2=(a﹣2)2+(a2﹣4a+4)2,
①若OB2=OA2+AB2,则a2+(a2﹣4a)2=20+(a﹣2)2+(a2﹣4a+4)2,
解得a=2(舍)或,
∴,,
∴直线OB解析式为,
当x=2时,y=﹣3,即P(2,﹣3),
∴;
②若AB2=OA2+OB2,则(a﹣2)2+(a2﹣4a+4)2=20+a2+(a2﹣4a)2,
解得a=0(舍)或,
∴,,
∴直线OB解析式为,
当x=2时,y=1,即P(2,1),
∴;
③若OA2=AB2+OB2,则20=(a﹣2)2+(a2﹣4a+4)2+a2+(a2﹣4a)2,
整理,得:a3﹣8a2+21a﹣18=0,
∴a3﹣3a2﹣5a2+15a+6a﹣18
=a2(a﹣3)﹣5a(a﹣3)+6(a﹣3)
=(a﹣3)(a2﹣5a+6)
=(a﹣3)2(a﹣2)
=0,
∴a=3或a=2(舍),
∴B(3,﹣3),
∴直线OB解析式为y=﹣x,
当x=2时,y=﹣2,即P(2,﹣2),
∴;
综上所述,当△AOB为直角三角形时,t的值为2或4或10.
同课章节目录
