21.3二次根式的加减法 华师大版数学九年级上册 课件1(共23张PPT)
文档属性
| 名称 | 21.3二次根式的加减法 华师大版数学九年级上册 课件1(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 625.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-22 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
导入新课
讲授新课
当堂练习
课堂小结
第21章
二次根式
21.3
二次根式的加减
1.探索二次根式加减运算的步骤和方法;(重点)
2.了解二次根式的混合运算可类比整式的混合运算及数的混合运算;(重点)
3.准确熟练地进行二次根式的混合运算.(难点)
学习目标
二次根式计算、化简的结果符合什么要求?
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式.
导入新课
回顾思考
观察下列二次根式有什么共同特征:
(1)
…
, ,
,
(2)
…
,
,
,
每组的二次根式的被开方数相同
讲授新课
同类二次根式
探究归纳
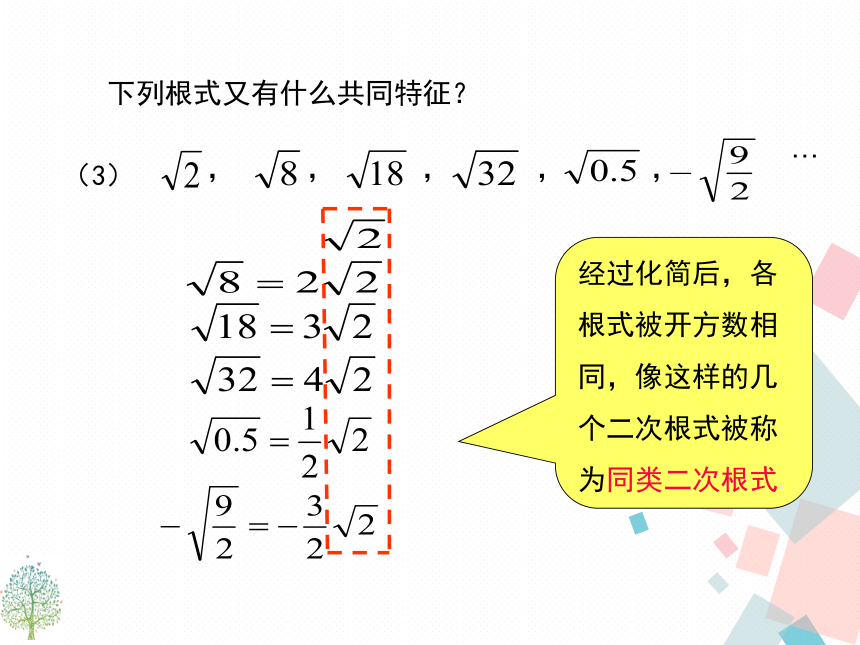
,
, , , ,
(3)
…
经过化简后,各根式被开方数相同,像这样的几个二次根式被称为同类二次根式.
下列根式又有什么共同特征?
(1)说出
的三个同类二次根式;
(2)下列各式中哪些是同类二次根式?
巩固概念:
答案不唯一,如
先化成最简二次根式,再作判断.
答:
问题
现有一块长7.5dm、宽5dm的木板,能否采用如图的方式,在这块木板上截出两个分别是8dm2和18dm2的正方形木板?
7.5dm
5dm
二次根式的加减法则及运用
(化成最简二次根式)
(逆用分配律)
∴在这块木板上可以截出两个分别是8dm2和18dm2的正方形木板.
解:列式如下:
思考:如何合并同类二次根式?
合并同类二次根式的方法是:
(1)化为最简二次根式
(2)系数相加减
(3)二次根式不变
二次根式的加减法则
类比合并同类项,说说计算过程有什么规律?
二次根式加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式(同类二次根式)进行合并.
一化
二找
三合并
知识要点
例
计算
提示
按照二次根式的加减法则进行,即先化简,后判定,再合并.
典例精析
解:
比较二次根式的加减与整式的加减,你能得出什么结论?
二次根式的加减实质是合并同类二次根式(被开方数相同).
整式的加减的实质是合并同类项.
(1)
(2)
计算:
思考:(1)中,先计算什么?后计算什么,最后的目标是什么?(2)呢?
二次根式的混合运算方法
典例精析
与有理数、实数运算一样,在混合运算中先乘除,
后加减;
对于(1):先算乘,再化简,若有相同的二次根
式进行合并,最后的目标是二次根式是最简二次根式;
对于(2):先算除,再化简,若有相同的二次根
式进行合并,把所有的二次根式化成最简二次根式.
解:
(1)
思考:(1)中,每一步的依据是什么?
第一步的依据是:分配律或多项式乘单项式;
第二步的依据是:二次根式乘法法则;
第三步的依据是:二次根式化简.
解:
(2)
思考:(2)中,每一步的依据是什么?
第一步的依据是:多项式除以单项式法则;
第二步的依据是:二次根式除法法则.
二次根式的加、减、乘、除混合运算与整式运算一样,体现在:运算律、运算顺序、乘法法则、乘法公式仍然适用.
平方差公式:(a+b)(a-b)=a2-b2;
(a+b)2=a2+2ab+b2;
(a-b)2=a2-2ab+b2;
完全平方公式
知识要点
1.计算
解:
解:
解题反思:(1)有括号的先去括号再进行运算;
(2)被开方数不相同的最简二次根式是不能合并的.
当堂练习
2.
计算:
(1)
(2)
(3)
提示
把二次根式看成“项”,(1)、(2)、(3)分别可以看成整式乘法中“单项式×多项式”、“多项式÷单项式”、“多项式×多项式”的运算.
看看和你做的一样吗?
(1)
解:
(2)
(3)
3.
计算:
用了公式(a+b)(a-b)
=a2-b2.
用了公式(a+b)2
=a2+2ab+b2.
1.同类二次根式的定义.
2.二次根式加减运算的步骤:
(1)把各个二次根式化成最简二次根式;
(2)把各个同类二次根式合并.
3.如何合并同类二次根式
与合并同类项类似,把同类二次根式的系数相加减,作为结果的系数,根号及根号内部都不变.
几个二次根式化成最简二次根式后,如果被开方数相同,这几个二次根式就叫做同类二次根式.
课堂小结
谈一谈本节课自己的收获和感受?
(1)
以前学过的运算法则在二次根式的混合运算中依然成立;
(2)计算结果最后一定要化成最简形式;
(3)二次根式的混合运算与整式的运算非常类似,即运算性质
和运算律是一致的,体现了数式通性的特点;
(4)计算时要做到准确熟练.
导入新课
讲授新课
当堂练习
课堂小结
第21章
二次根式
21.3
二次根式的加减
1.探索二次根式加减运算的步骤和方法;(重点)
2.了解二次根式的混合运算可类比整式的混合运算及数的混合运算;(重点)
3.准确熟练地进行二次根式的混合运算.(难点)
学习目标
二次根式计算、化简的结果符合什么要求?
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式.
导入新课
回顾思考
观察下列二次根式有什么共同特征:
(1)
…
, ,
,
(2)
…
,
,
,
每组的二次根式的被开方数相同
讲授新课
同类二次根式
探究归纳
,
, , , ,
(3)
…
经过化简后,各根式被开方数相同,像这样的几个二次根式被称为同类二次根式.
下列根式又有什么共同特征?
(1)说出
的三个同类二次根式;
(2)下列各式中哪些是同类二次根式?
巩固概念:
答案不唯一,如
先化成最简二次根式,再作判断.
答:
问题
现有一块长7.5dm、宽5dm的木板,能否采用如图的方式,在这块木板上截出两个分别是8dm2和18dm2的正方形木板?
7.5dm
5dm
二次根式的加减法则及运用
(化成最简二次根式)
(逆用分配律)
∴在这块木板上可以截出两个分别是8dm2和18dm2的正方形木板.
解:列式如下:
思考:如何合并同类二次根式?
合并同类二次根式的方法是:
(1)化为最简二次根式
(2)系数相加减
(3)二次根式不变
二次根式的加减法则
类比合并同类项,说说计算过程有什么规律?
二次根式加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式(同类二次根式)进行合并.
一化
二找
三合并
知识要点
例
计算
提示
按照二次根式的加减法则进行,即先化简,后判定,再合并.
典例精析
解:
比较二次根式的加减与整式的加减,你能得出什么结论?
二次根式的加减实质是合并同类二次根式(被开方数相同).
整式的加减的实质是合并同类项.
(1)
(2)
计算:
思考:(1)中,先计算什么?后计算什么,最后的目标是什么?(2)呢?
二次根式的混合运算方法
典例精析
与有理数、实数运算一样,在混合运算中先乘除,
后加减;
对于(1):先算乘,再化简,若有相同的二次根
式进行合并,最后的目标是二次根式是最简二次根式;
对于(2):先算除,再化简,若有相同的二次根
式进行合并,把所有的二次根式化成最简二次根式.
解:
(1)
思考:(1)中,每一步的依据是什么?
第一步的依据是:分配律或多项式乘单项式;
第二步的依据是:二次根式乘法法则;
第三步的依据是:二次根式化简.
解:
(2)
思考:(2)中,每一步的依据是什么?
第一步的依据是:多项式除以单项式法则;
第二步的依据是:二次根式除法法则.
二次根式的加、减、乘、除混合运算与整式运算一样,体现在:运算律、运算顺序、乘法法则、乘法公式仍然适用.
平方差公式:(a+b)(a-b)=a2-b2;
(a+b)2=a2+2ab+b2;
(a-b)2=a2-2ab+b2;
完全平方公式
知识要点
1.计算
解:
解:
解题反思:(1)有括号的先去括号再进行运算;
(2)被开方数不相同的最简二次根式是不能合并的.
当堂练习
2.
计算:
(1)
(2)
(3)
提示
把二次根式看成“项”,(1)、(2)、(3)分别可以看成整式乘法中“单项式×多项式”、“多项式÷单项式”、“多项式×多项式”的运算.
看看和你做的一样吗?
(1)
解:
(2)
(3)
3.
计算:
用了公式(a+b)(a-b)
=a2-b2.
用了公式(a+b)2
=a2+2ab+b2.
1.同类二次根式的定义.
2.二次根式加减运算的步骤:
(1)把各个二次根式化成最简二次根式;
(2)把各个同类二次根式合并.
3.如何合并同类二次根式
与合并同类项类似,把同类二次根式的系数相加减,作为结果的系数,根号及根号内部都不变.
几个二次根式化成最简二次根式后,如果被开方数相同,这几个二次根式就叫做同类二次根式.
课堂小结
谈一谈本节课自己的收获和感受?
(1)
以前学过的运算法则在二次根式的混合运算中依然成立;
(2)计算结果最后一定要化成最简形式;
(3)二次根式的混合运算与整式的运算非常类似,即运算性质
和运算律是一致的,体现了数式通性的特点;
(4)计算时要做到准确熟练.
