2021-2022学年九年级数学人教版上册《22.3实际问题与二次函数》能力提升训练(word解析版)
文档属性
| 名称 | 2021-2022学年九年级数学人教版上册《22.3实际问题与二次函数》能力提升训练(word解析版) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-23 00:00:00 | ||
图片预览




文档简介
2021-2022学年人教版九年级数学上册《22.3实际问题与二次函数》能力提升训练(附答案)
一、选择题
1.如图,抛物线y=x+2交x轴于点A,B,交y轴于点C,当△ABC纸片上的点C沿着此抛物线运动时,则△ABC纸片随之也跟着水平移动,设纸片上BC的中点M坐标为(m,n),在此运动过程中,n与m的关系式是( )
A.n=(m﹣)2﹣
B.n=(m﹣)2
C.n=(m﹣)2﹣
D.n=(m﹣)2﹣
2.苏州市“东方之门”是由两栋超高层建筑组成的双塔连体建筑,“门”的造型是东方之门的立意基础,“门”的内侧曲线呈抛物线型,如图1,两栋建筑第八层由一条长60m的连桥连接,在该抛物线两侧距连桥150m处各有一窗户,两窗户的水平距离为30m,如图2,则此抛物线顶端O到连桥AB距离为( )
A.180m
B.200m
C.220m
D.240m
3.如图,直线y=与y轴交于点A,与直线y=﹣交于点B,以AB为边向右作菱形ABCD,点C恰与原点O重合,抛物线y=(x﹣h)2+k的顶点在直线y=﹣上移动.若抛物线与菱形的边AB、BC都有公共点,则h的取值范围是( )
A.﹣2
B.﹣2≤h≤1
C.﹣1
D.﹣1
4.为测量某地温度变化情况,记录了一段时间的温度.一段时间内,温度y与时间t的函数关系满足y=﹣t2+12t+2,当4≤t≤8时,该地区的最高温度是( )
A.38℃
B.37℃
C.36℃
D.34℃
5.如图1,一个移动喷灌架喷射出的水流可以近似地看成抛物线.图2是喷灌架为一坡地草坪喷水的平面示意图,喷水头的高度(喷水头距喷灌架底部的距离)是1米.当喷射出的水流距离喷水头20米时,达到最大高度11米,现将喷灌架置于坡度为1:10的坡地底部点O处,草坡上距离O的水平距离为30米处有一棵高度约为2.3米的石榴树AB,因为刚刚被喷洒了农药,近期不能被喷灌.下列说法正确的是( )
A.水流运行轨迹满足函数y=﹣x2﹣x+1
B.水流喷射的最远水平距离是40米
C.喷射出的水流与坡面OA之间的最大铅直高度是9.1米
D.若将喷灌架向后移动7米,可以避开对这棵石榴树的喷灌
6.如图,Rt△OAB的顶点A(﹣2,4)在抛物线y=ax2上,将Rt△OAB绕点O顺时针旋转90°,得到△OCD,边CD与该抛物线交于点P,则点P的坐标为( )
(,)
B.(2,2)
C.(,2)
D.(2,)
7.如图,在平面直角坐标系中,抛物线y=x2+bx+c与x轴交于A、B两点,点A在x轴的负半轴,点B在x轴的正半轴,与y轴交于点C,且CO=2AO,CO=BO,AB=3.则下列判断中正确的是( )
A.此抛物线的解析式为y=x2+x﹣2
B.当x>0时,y随着x的增大而增大
C.此抛物线与直线y=只有一个交点
D.在此抛物线上的某点M,使△MAB的面积等于4,这样的点共有三个
二、填空题
8.用一根长为20cm的铁丝围成一个矩形,该矩形面积的最大值是
cm2.
9.京剧作为一门中国文化的传承艺术,常常受到外国友人的青睐.如图,在平面直角坐标系xOy中,某脸谱轮廓可以近似地看成是一个半圆与抛物线的一部分组合成的封闭图形,记作图形G.点A,B,C,D分别是图形G与坐标轴的交点,已知点D的坐标为(0,﹣3),AB为半圆的直径,且AB=4,半圆圆心M的坐标为(1,0).关于图形G给出下列四个结论,其中正确的是
(填序号).
①图形G关于直线x=1对称;②线段CD的长为3+;
③图形G围成区域内(不含边界)恰有12个整点(即横、纵坐标均为整数的点);
④当﹣4≤a≤2时,直线y=a与图形G有两个公共点.
10.如图,直线y=kx+b交坐标轴于A、B两点,交抛物线y=ax2于点C(4,3),且C是线段AB的中点,抛物线上另有位于第一象限内的一点P,过P的直线y=k′x+b′交坐标轴于D、E两点,且P恰好是线段DE的中点,若△AOB∽△DOE,则P点的坐标是
.
11.如图1,AO,BC是两根垂直于地面的立柱,且长度相等.在两根立柱之间悬挂着一根绳子,如图2建立坐标系,绳子形如抛物线y=﹣x+4的图象.因实际需要,在OA与BC间用一根高为2.5m的立柱MN将绳子撑起,若立柱MN到OA的水平距离为3m,MN左侧抛物线的最低点D与MN的水平距离为1m,则点D到地面的距离为
.
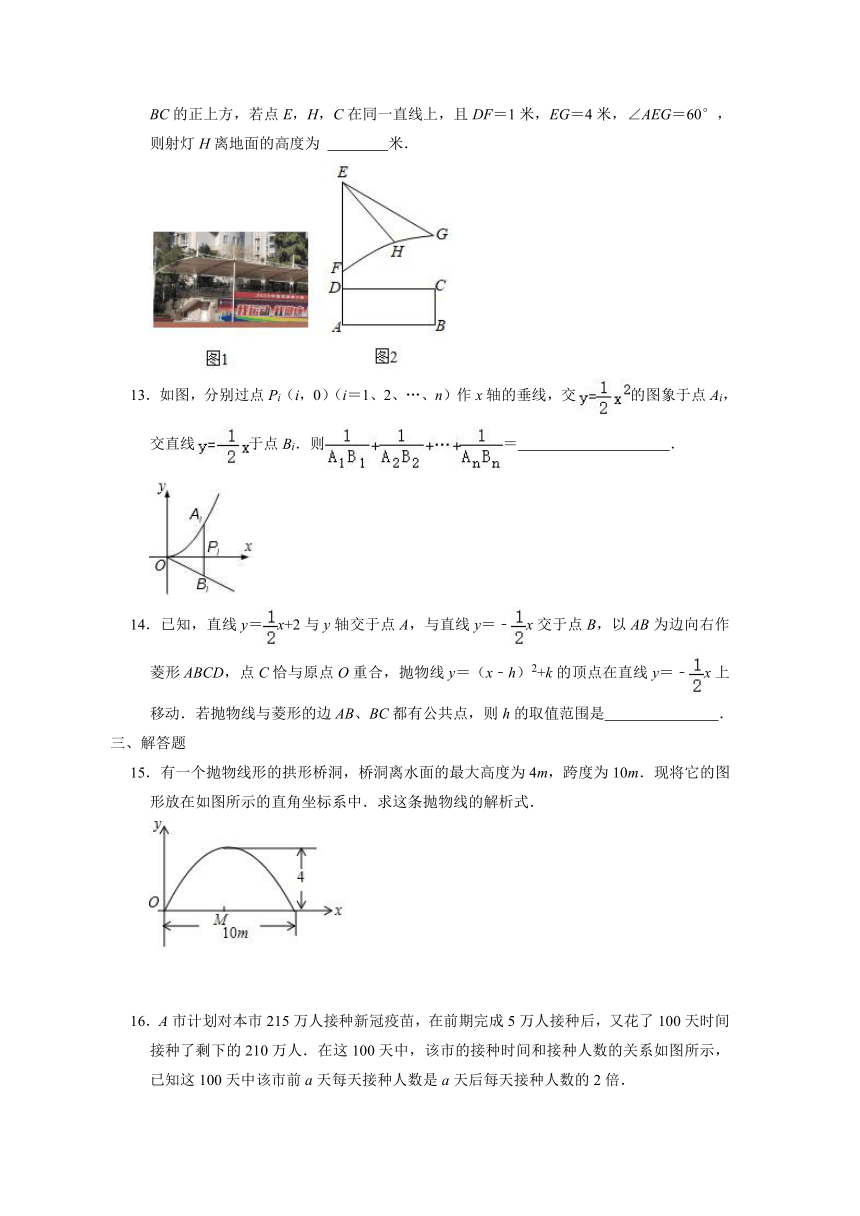
12.如图1是某校园运动场主席台及遮阳棚,其侧面结构示意图如图2所示.主席台(矩形ABCD)高AD=2米,直杆DE=5米,斜拉杆EG,EH起稳固作用,点H处装有一射灯.遮阳棚边缘曲线FHG可近似看成抛物线的一部分,G为抛物线的最高点且位于主席台边缘BC的正上方,若点E,H,C在同一直线上,且DF=1米,EG=4米,∠AEG=60°,则射灯H离地面的高度为
米.
13.如图,分别过点Pi(i,0)(i=1、2、…、n)作x轴的垂线,交的图象于点Ai,交直线于点Bi.则=
.
已知,直线y=x+2与y轴交于点A,与直线y=﹣x交于点B,以AB为边向右作菱形ABCD,点C恰与原点O重合,抛物线y=(x﹣h)2+k的顶点在直线y=﹣x上移动.若抛物线与菱形的边AB、BC都有公共点,则h的取值范围是
.
三、解答题
15.有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为4m,跨度为10m.现将它的图形放在如图所示的直角坐标系中.求这条抛物线的解析式.
16.A市计划对本市215万人接种新冠疫苗,在前期完成5万人接种后,又花了100天时间接种了剩下的210万人.在这100天中,该市的接种时间和接种人数的关系如图所示,已知这100天中该市前a天每天接种人数是a天后每天接种人数的2倍.
(1)求a的值;
(2)这100天中,B市的接种人数y(万人)与接种天数x(天)的关系为y=x2+x,
①请通过计算判断,第a天接种完成后,B市的接种人数是否超过A市?
②第几天接种完成后,A,B两市接种人数恰好相同?
17.商场购进一批儿童智力玩具,调查发现:该玩具的月销售量y(个)与销售单价x(元)之间满足一次函数关系,下表是销售单价与月销售量、月销售利润的对应值分别如下:
月销售单价x(元/个)
30
35
40
45
月销售量y(个)
230
180
130
m
月销售利润w(元)
2300
2700
2600
2000
(1)直接写出y与x的函数关系式
;
(2)根据以上信息填空:
①m=
;该商场购进玩具单价
元/个;
②求w与x的函数关系式,并求出当销售单价x定为多少时,月销售利润最大?
(3)由于生产玩具成本增加,商场购进玩具单价提高n元/个(0<n≤7,n为整数),商场规定每件玩具售价不能低于40元/个,该商场在今后的销售中,月销售量与售价仍然满足(1)中的函数关系.若月销售最大利润是2340元,则n的值是
.
18.某超市购进一种商品,进货单价为每件10元,在销售过程中超市按相关规定,销售单价不低于1元且不高于19元.如果该商品的销售单价x(单位:元/件)与日销售量y(单位:件)满足一次函数关系y=﹣2x+40,设该商品的日销售利润为w元,那么当该商品的销售单价x(元/件)定为多少时,日销售利润最大?最大利润是多少元?
19.某单位为响应市“创建全国文明城市”的号召,不断美化环境,拟在一块矩形空地上修建绿色植物园,其中一边靠墙,可利用的墙长不超过18m,另外三边由36m长的栅栏围成.设矩形ABCD空地中,垂直于墙的边AB=xm,面积为ym2(如图).
(1)求y与x之间的函数关系式,并求出自变量x的取值范围;
(2)若矩形空地的面积为160m2,求x的值;
(3)当矩形ABCD空地的面积最大时,利用的墙长是多少m;并求此时的最大面积.
20.2020年是脱贫攻坚的收官之年,老李在驻村干部的帮助下,利用网络平台进行“直播带货”,销售一批成本为每件30元的商品,按单价不低于成本价,且不高于50元销售,经调查发现,该商品每天的销售量y(件)与销售单价x(元)之间满足一次函数关系,部分数据如表所示.
销售单价x(元)
30
40
45
销售数量y(件)
100
80
70
(1)求该商品每天的销售量y(件)与销售单价x(元)之间的函数关系式;
(2)销售单价定为多少元时,每天的销售利润为800元?
(3)销售单价定为多少元时,才能使销售该商品每天获得的利润w(元)最大?最大利润是多少元?
21.2020年,新型冠状病毒肆虐,给人们的生活带来许多不便,网络销售成为这个时期最重要的一种销售方式.某乡镇农贸公司新开设了一家网店,销售当地农产品.其中一种当地特产在网上试销售,其成本为每千克2元.公司在试销售期间,调查发现,每天销售量y(kg)与销售单价x(元)满足如图所示的函数关系(其中2<x≤10).
(1)求y与x之间的函数关系式;
(2)销售单价x为多少元时,每天的销售利润最大?最大利润是多少元?
22.小明投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:y=﹣10x+500,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.
(1)设小明每月获得利润为w(元),求每月获得利润w(元)与销售单价x(元)之间的函数关系式,并确定自变量x的取值范围.
(2)当销售单价定为多少元时,每月可获得最大利润?每月的最大利润是多少?
23.如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象与直线AB交于A、B两点,A(1,﹣),B(﹣2,0),其中点A是抛物线y=ax2+bx+c的顶点,交y轴于点D.
(1)求二次函数解析式;
(2)如图1,点P是第四象限抛物线上一点,且满足BP∥AD,抛物线交x轴于点C.M为直线AB下方抛物线上一点,过点M作PC平行线交BP于点N,求MN最大值;
(3)如图2,点Q是抛物线第三象限上一点(不与点B、D重合),连接BQ,以BQ为边作正方形BEFQ,当顶点E或F恰好落在抛物线对称轴上时,直接写出对应的Q点的坐标.
24.如图,抛物线y=x2﹣x﹣与x轴交于点A和点B,与y轴交于点C,经过点C的直线l与抛物线交于另一点E(4,a),抛物线的顶点为点Q,抛物线的对称轴与x轴交于点D.
(1)求直线CE的解析式.
(2)如图2,P为直线CE下方抛物线上一动点,直线CE与x轴交于点F,连接PF,PC.当△PCF的面积最大时,求点P的坐标及△PCF面积的最大值.
(3)如图3,连接CD,将(1)中抛物线沿射线CD平移得到新抛物线y′,y′经过点D,y′的顶点为点H,在直线QH上是否存在点G,使得△DQG为等腰三角形?若存在,求出点G的坐标.
25.如图所示,某河面上有一座抛物线形拱桥,桥下水面在正常水位AB时,宽为20m,若水位上升3m,水面就会达到警戒线CD,这时水面宽为10m.
(1)建立适当的平面直角坐标系并求出抛物线的解析式;
(2)若洪水到来时,水位以每小时0.2m的速度上升,从警戒线开始,再持续多少小时就能到达拱桥的拱顶?
26.商店购进一批单价为20元的T恤,经试验发现,每天销售件数y(件)与销售价格x(元/件)满足图中的一次函数关系.
(1)求y与x满足的函数表达式(不要求写出x的取值范围).
(2)在不积压且不考虑其他因素的情况下,销售价格定为多少元/件时,才能使每天获得的利润W最大?
27.某公司经营杨梅业务,以3万元/吨的价格向农户收购杨梅后,分拣成A、B两类,A类杨梅包装后直接销售;B类杨梅深加工后再销售A类杨梅的包装成本为1万元/吨,根据市场调查,它的平均销售价格y(单位:万元/吨)与销售数量x(x≥2)之间的函数关系如图;B类杨梅深加工总费用s(单位:万元)与加工数量t(单位:吨)之间的函数关系是s=12+3t,平均销售价格为9万元/吨.
(1)直接写出A类杨梅平均销售价格y与销售量x之间的函数关系式;
(2)第一次,该公司收购了20吨杨梅,其中A类杨梅有x吨,经营这批杨梅所获得的总利润为w万元,求w关于x的函数关系式;
(3)第二次,该公司准备投入132万元资金,请设计一种经营方案,使公司获得最大利润,并求出最大利润.
28.疫情期间,按照防疫要求,学生在进校时必须排队接受体温检测.某校统计了学生早晨到校情况,发现从7:00开始,在校门口的学生人数y(单位:人)随时间x(单位:分钟)的变化情况的图象是二次函数的一部分,如图所示.
(1)求y与x之间的函数解析式;
(2)从7:00开始,需要多少分钟校门口的学生才能全部进校?
(3)现学校通过调整校门口的入校通道,提高体温检测效率.经过调整,现在每分钟可以多通过2人,请问所有学生能够在7点30分完成进校吗?请说明理由.
29.为推进“世界著名花城”建设,深圳多个公园近期举办花展活动.某公园想用一段长为80米的篱笆,围成一个一边靠围墙的ABCD,墙长36米.
(1)当AB长为多少米时所围成的花圃面积最大?最大值是多少?
(2)当花圃的面积为350平方米时,AB长为多少米?
30.今年甲、乙两个果园的红心猕猴桃喜获丰收,已知甲果园的总产量为27吨,乙果园的总产量13吨,某果业公司租用A、B两种型号的保鲜货车去果园运输猕猴桃,甲果园需要A型保鲜货车满载猕猴桃运输6趟,同时需要B型保鲜货车满载猕猴桃运输5趟才能刚好运输完:乙果园需A型保鲜货车满载猕猴桃运输2趟,同时需要B型保鲜货车满载猕猴桃运输3趟刚好运输完.
(1)求A、B两种保鲜货车满载猕猴桃运输一趟分别是多少吨?
(2)果业公司收购该批猕猴桃的单价为0.8万元/吨,目前公司可以0.9万元/吨的价格售出,如果保鲜冷藏储存起来,旺市再销售以便获取最大利润,由于失水和腐烂,水果重量每天减少0.5吨,且每天需支付各种费用0.08万元/吨,而每天的价格会持续上涨0.1万元/吨、如果公司计划把该批猕猴桃最多保鲜冷藏储存20天,那么储存多少天后出售这批猕猴桃所获得的利润最大?最大利润是多少万元?
31.开学初,小明到文具批发部一次性购买某种笔记本,该文具批发部规定:这种笔记本售价y(元/本)与购买数量x(本)之间的函数关系如图所示.
(1)图中线段AB所表示的实际意义是
;
(2)请直接写出y与x之间的函数关系式;
(3)已知该文具批发部这种笔记本的进价是3元/本,若小明购买此种笔记本超过15本但不超过25本,那么小明购买多少本时,该文具批发部在这次买卖中所获的利润W(元)最大?最大利润是多少?
32.某景区纪念品超市以50元每个的价格新进一批工艺摆件,经过一段时间的销售发现日销量y(个)与单个售价x(元)之间的函数关系如图.(景区规定任何商品的利润率不得高于90%)
(1)根据图象,直接写出y与x的函数关系式;
(2)该超市要想每天获得2400元的销售利润,销售单价应定为多少元?
(3)销售单价为多少元时,每天获得的利润最大,最大利润是多少元?
33.在“新冠”疫情期间,全国人民“众志成城,同心抗疫”,某商家决定将一个月获得的利润全部捐赠给社区用于抗疫.已知商家购进一批产品,成本为10元/件,拟采取线上和线下两种方式进行销售.调查发现,线下的月销量y(单位:件)与线下售价x(单位:元/件,12≤x<24)满足一次函数的关系,部分数据如下表:
x(元/件)
12
13
14
15
16
y(件)
1200
1100
1000
900
800
(1)求y与x的函数关系式;
(2)若线上售价始终比线下每件便宜2元,且线上的月销量固定为400件,试问:当x为多少时,线上和线下月利润总和达到最大?
34.某种水果每千克进价20元,每千克售价x元(30<x<50),每天的销售量为(﹣x+50)千克.
(1)求每天获得利润(用含x的代数式表示);
(2)当每千克售价为多少元时,每天可获得最大利润?
(3)若每天获得利润200元,那么每千克售价应该定为多少元?
35.如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A、B
(点A在点B的左边),与y轴交于点C,点A、C的坐标分别为(﹣3,0)、(0,2),对称轴为直线x=﹣2.
(1)求抛物线的解析式;
(2)如图,点D与点C关于抛物线的对称轴对称,连接AC,过点D作DE∥AC交抛物线于点E,交y轴于点M.点F是直线AC下方抛物线上的一动点,连接DF交AC于点G,连接EG,求△EFG的面积的最大值以及取得最大值时点F的坐标;
(3)在(2)的条件下,点P为平面内一点,在抛物线上是否存在一点Q,是以点P、Q、F、C为顶点的四边形为矩形,如果存在,直接写出点P的坐标,如果不存在,说明理由.
36.如图,顶点为P(m,m)(m>0)的二次函数图象与x轴交于点A(2m,0),点B在该图象上,直线OB交二次函数图象对称轴l于点M,点M、N关于点P对称,连接BN、ON.
(1)求该二次函数的关系式(用含m的式子表示);
(2)若点B在对称轴l右侧的二次函数图象上运动,请解答下列问题:
①连接OP,当OP=MN时,请判断△NOB的形状,并说明理由.
②求证:∠BNM=∠ONM.
37.如图,直线l:y=﹣3x+3与x轴、y轴分别相交于A、B两点,抛物线y=ax2﹣2ax﹣3a(a<0)经过点B.
(1)求该抛物线的函数表达式;
(2)已知点M是抛物线上的一个动点,并且点M在第一象限内,连接AM、BM,设点M的横坐标为m,△ABM的面积为S,求S与m的函数表达式,并求出S的最大值;
(3)在(2)的条件下,当S取得最大值时,动点M相应的位置记为点M′.将直线l绕点A按顺时针方向旋转得到直线l′,当直线l′与直线AM′重合时停止旋转,在旋转过程中,直线l′与线段BM′交于点C,设点B、M′到直线l′的距离分别为d1、d2,当d1+d2最大时,求直线l′旋转的角度(即∠BAC的度数).
38.如图,已知抛物线y=ax2+bx﹣3(a≠0)与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,顶点D的坐标为(1,﹣4),连接AD.直线y=﹣x+c经过点B,且与y轴交于点E.
(1)求抛物线的解析式及c的值.
(2)点N为抛物线在y轴右侧的部分上一点,当△ADN是以DN为腰的等腰三角形时,求点N的坐标.
(3)点F为线段BE上一点,点G为线段OB上一点,连接FC,FG的延长线与线段AD交于点H,当∠EFG=3∠ABE,且GH=2FG时,直接写出点F的横坐标.
39.将抛物线C:y=(x﹣2)2向下平移6个单位长度得到抛物线C1,再将抛物线C1向左平移2个单位长度得到抛物线C2.
(1)直接写出抛物线C1,C2的解析式;
(2)如图(1),点A在抛物线C1(对称轴l右侧)上,点B在对称轴l上,△OAB是以OB为斜边的等腰直角三角形,求点A的坐标;
(3)如图(2),直线y=kx(k≠0,k为常数)与抛物线C2交于E,F两点,M为线段EF的中点;直线y=﹣x与抛物线C2交于G,H两点,N为线段GH的中点.求证:直线MN经过一个定点.
40.如图1,已知抛物线y=ax2+bx经过点A(4,0)、B(,).
(1)直接写出抛物线的解析式和顶点G的坐标;
(2)如图2,点C、D是线段OA上的两点(不含端点),过C、D分别作x轴的垂线,交抛物线于点E、F.设P是第三象限内抛物线上任意一点,连接PE和PF,分别交y轴于点M、N.求证:MC∥ND;
(3)如图3,直线y=kx(k>0)交抛物线于另一点于Q.当∠OQG=90°时,求k的值.
41.如图,在平面直角坐标系中,已知抛物线y=x2﹣4x+3与x轴交于A,B两点,点A在点B的左侧,与y轴交于点C,其顶点为点D,点E的坐标为(0,),该抛物线与BE交于另一点F,连接BC.
(1)求点A,B,C的坐标;
(2)动点M从点D出发,沿抛物线对称轴方向向下以每秒1个单位的速度运动,运动时间为t,连接OM,BM,当t为何值时,△OMB为等腰三角形?
(3)在x轴下方的抛物线上,是否存在点P,使得∠PBF被BA平分?若存在,请求出点P的坐标;若不存在,请说明理由.
42.如图1,已知抛物线y=x2+bx+c与x轴交于A(﹣1,0)、B(3,0)两点,与y轴交于点C,顶点为点D.
(1)求该抛物线的函数表达式;
(2)点E是点D关于x轴的对称点,经过点A的直线y=mx+1与该抛物线交于点F,点P是直线AF上的一个动点,连接AE、PE、PB,记△PAE的面积为S1,△PAB的面积为S2,那么的值是否是定值?如果是,请求出这个定值;如果不是,请说明理由.
(3)如图2,设直线AC与直线BD交于点M,点N是直线AC上一点,若∠ONC=∠BMC,求点N的坐标.
43.点A,B在抛物线y=ax2(a>0)上,AB交y轴于点C.
(1)过点C作DC⊥y轴交抛物线于点D,若AB∥OD,AB的解析式为y=x+2,求a的值;
(2)若点C(0,2)过点B作BG⊥x轴交x轴于点G,BG的延长线交AO的延长线于点H,连接AG交y轴于点K,求OK?BH的值;
(3)若a=1,将抛物线平移后交x轴于点A(﹣1,0),B(2,0)两点,点P为y轴正半轴上一点,AP,BP交抛物线于点M,N,设△PNA的面积为S1,△PMB的面积为S2,△PBA的面积为S3,若,求点P的坐标.
参考答案
1.解:∵抛物线y=x+2交x轴于点A,B,交y轴于点C,
∴点B的坐标为(4,0),点C的坐标为(0,2),
∴BC的中点M坐标为(,),即点M坐标为(2,1).
∵点C沿着此抛物线运动,点M也随之运动,点M的运动轨迹是抛物线,且经过(2,1),(6,﹣1)
∴设抛物线的解析式为y=x2+bx+c,
则有,解得
∴m,n满足,n=m2﹣m+8=(m﹣)2﹣,
故选:D.
2.解:以AB所在的直线为x轴,以线段AB的垂直平分线所在的直线为y轴建立平面直角坐标系:
∴A(﹣30,0),B(30,0),D(15,150),
设抛物线的解析式为y=a(x+30)(x﹣30),将(15,150)代入,得:
150=a(15+30)(15﹣30),
解得:a=﹣,
∴y=﹣(x+30)(x﹣30)
=﹣x2+200,
∴抛物线顶端O的坐标为(0,200),
∴此抛物线顶端O到连桥AB距离为200m.
故选:B.
3.解:∵将y=与y=﹣联立得:,解得:.
∴点B的坐标为(﹣2,1).
由抛物线的解析式可知抛物线的顶点坐标为(h,k).
∵将x=h,y=k,代入得y=﹣得:﹣h=k,解得k=﹣,
∴抛物线的解析式为y=(x﹣h)2﹣h.
如图1所示:当抛物线经过点C时.
将C(0,0)代入y=(x﹣h)2﹣h得:h2﹣h=0,解得:h1=0(舍去),h2=.
如图2所示:当抛物线经过点B时.
将B(﹣2,1)代入y=(x﹣h)2﹣h得:(﹣2﹣h)2﹣h=1,整理得:2h2+7h+6=0,解得:h1=﹣2,h2=﹣(舍去).
综上所述,h的范围是﹣2≤h≤.
故选:A.
4.解:∵y=﹣t2+12t+2
=﹣(t2﹣12t+36)+38
=﹣(t﹣6)2+38,
∴当t=6时,温度y有最大值,最大值为38℃.
∴当4≤t≤8时,该地区的最高温度是38℃.
故选:A.
5.解:由题意可设抛物线的解析式为y=a(x﹣20)2+k,
将(0,1),(20,11)分别代入,得:,解得:,
∴y=﹣(x﹣20)2+11
=﹣x2+x+1,
故A错误;
∵坡度为1:10,
∴直线OA的解析式为y=0.1x,
当x=40时,y=0.1×40=4,
令y=4,得﹣x2+x+1=4,
∴x2﹣40x+120=0,
解得x=20±2≠40,
∴B错误;
设喷射出的水流与坡面OA之间的铅直高度为h米,
则h=﹣x2+x+1﹣0.1x=﹣x2+x+1,
∴对称轴为x=﹣=18,
∴hmax=9.1,故C正确;
将喷灌架向后移动7米,则图2中x=30时抛物线上的点的纵坐标值等于x=37时的函数值,
当x=37时,y=﹣×372+37+1=3.775,
在图2中,当x=30时,点B的纵坐标为:0.1×30+2.3=5.3,
则点A的纵坐标为5.3﹣2.3=3<3.775,故D错误.
故选:C.
6.解:∵Rt△OAB的顶点A(﹣2,4)在抛物线y=ax2上,
∴4=a×(﹣2)2,
解得:a=1
∴解析式为y=x2,
∵Rt△OAB的顶点A(﹣2,4),
∴OB=OD=2,
∵Rt△OAB绕点O顺时针旋转90°,得到△OCD,
∴CD∥x轴,
∴点D和点P的纵坐标均为2,
∴令y=2,得2=x2,
解得:x=±,
∵点P在第一象限,
∴点P的坐标为:(,2)
故选:C.
7.解:∵CO=2AO,而CO=BO,AB=3,
∴AO=1,BO=OC=2,即A(﹣1,0),B(2,0),C(0,﹣2),
∴二次函数的解析式为y=x2﹣x﹣2,故A错误.
∵二次函数的对称轴为x=,
∴当x>0时,y随着x的增大而先减小再增大,故B错误.
∵此二次函数的最小值为﹣,
∴此抛物线与直线y=﹣只有一个交点,C正确.
∵要使△MAB的面积等于4,须使M到x轴的距离为,这样的点共有2个,故D错误.
故选:C.
8.解:设矩形的长为xcm,则宽为(20÷2﹣x)cm,令矩形面积为ycm2,由题意得:
y=x(20÷2﹣x)
=x(10﹣x)
=﹣x2+10x
=﹣(x﹣5)2+25,
∴当x=5时,y有最大值为25,
∴该矩形面积的最大值是25cm2.
故答案为:25.
9.解:由图象可知图形G关于直线x=1对称,故①正确;
∵半圆圆心M的坐标为(1,0).
连接CM,如图:
∵AB=4,半圆圆心M的坐标为(1,0).
∴OM=1,MC=2,
∴OC==,
∵点D的坐标为(0,﹣3),
∴OD=3,
∴CD=OD+OC=3+,故②正确;
观察图象,可知图形G围成区域内(不含边界)恰有13个整点,故③错误;
由图象可知当a=﹣4或a=2时,直线y=a与图形G有一个公共点,故④错误.
综上,正确的有①②.
故答案为:①②.
10.解:∵抛物线y=ax2经过C(4,3),
∴抛物线的解析式为y=x2,
∵C是线段AB的中点,
∴B(0,6),A(8,0),
设点D的坐标为(0,a),
则点E的坐标为(a,0),
∵点P为DE的中点,
∴点P的坐标为(a,),
∵点P在抛物线y=x2上,
∴=×(a)2,
解得:a=,
∴点P的坐标为:(,),
设点D的坐标为(a,0),
则点E的坐标为(0,a),
∵点P为DE的中点,
∴点P的坐标为(,a),
∵点P在抛物线y=x2上,
∴a=×(a)2,
解得:a=8,
∴点P的坐标为:(4,3).
故答案为:(,)或(4,3).
11.解:∵抛物线的解析式为y=﹣x+4,
∴点A的坐标为(0,4),
∵立柱MN到OA的水平距离为3m,MN左侧抛物线的最低点D与MN的水平距离为1m,
∴点N左侧的抛物线的顶点的横坐标为2,点N的坐标为(3,),
设点N左侧的抛物线的解析式为y=a(x﹣2)2+k,把(0,4),(3,)分别代入解析式,得:
,
解得,
∴该抛物线的解析式为y=(x﹣2)2+2,
∴点D到地面的距离为2m.
故答案为:2m.
12.解:如图所示,以AB所在直线为x轴,AD所在直线为y轴,建立平面直角坐标系,过点G作GQ⊥AD于点G,
∵AD=2米,DE=5米,DF=1米,
∴D(0,2),E(0,7),F(0,3),
又∵GQ⊥AD,EG=4米,∠AEG=60°,
∴GQ=2(米),
∴EQ===2(米),
∴AQ=AE﹣EQ=7﹣2=5(米),
∴G(2,5),B(2,0),C(2,2),
∵点G为抛物线的顶点,
∴设抛物线的解析式为y=a+5(a≠0),将点F(0,3)代入,得:
3=a+5,
解得a=﹣,
∴抛物线的解析式为y=﹣+5,
设直线EC的解析式为y=kx+b(k≠0),将E(0,7),C(2,2)代入,得:
,
解得,
∴直线EC的解析式为y=﹣x+7,
联立,
解得,或(舍去),
∴H(,4.5),
∴射灯H离地面的高度为4.5米.
故答案为:4.5.
13.解:根据题意,知A1、A2、A3、…An的点都在函与直线x=i(i=1、2、…、n)的图象上,
B1、B2、B3、…Bn的点都在直线与直线x=i(i=1、2、…、n)图象上,
∴A1(1,)、A2(2,2)、A3(3,)…An(n,n2);
B1(1,﹣)、B2(2,﹣1)、B3(3,﹣)…Bn(n,﹣);
∴A1B1=|﹣(﹣)|=1,
A2B2=|2﹣(﹣1)|=3,
A3B3=|﹣(﹣)|=6,
…
AnBn=|n2﹣(﹣)|=;
∴=1,
=,
…
=.
∴,
=1++…+,
=2[+++…+],
=2(1﹣+﹣+﹣+…+﹣),
=2(1﹣),
=.
故答案为:.
14.解:把x=0代入y=x+2得:y=2,
∴A(0,2).
将y=x+2与y=﹣x联立,解得:x=﹣2,y=1,
∴B(﹣2,1).
∵抛物线y=(x﹣h)2+k的顶点在直线y=﹣x上,
∴抛物线的顶点坐标为(h,k)且k=﹣h.
∴抛物线的解析式为y=(x﹣h)2﹣h.
如图1所示:
当抛物线经过点C(O)时,抛物线恰好与BC、AB均有交点,
将点C(0,0)代入y=(x﹣h)2﹣h得:h2﹣h=0,解得h=0(舍去)或h=.
如图2所示:当抛物线经过点B时,抛物线恰好与BC、AB均有交点
此时点B恰好为抛物线的顶点,
∴h=﹣2.
∴当﹣2≤h≤时,抛物线与菱形的边AB、BC都有公共点.
故答案为:﹣2≤h≤.
15.解:由图象可知,
抛物线的顶点坐标为(5,4),过点(10,0),
设抛物线的解析式为:y=a(x﹣5)2+4,
则0=a(10﹣5)2+4,
解得,a=﹣,
即这条抛物线的解析式为:y=﹣(x﹣5)2+4.
16.解:(1)=2×,
解得a=40,
经检验a是原方程的根,
∴a的值为40;
(2)①把a=40代入y=x2+x,
得y=×402+×40=86<125,
答:第a天接种完成后,B市的接种人数没有超过A市;
②由题意前40天B市接种人数少于A市,
设A市接种人数与时间的函数关系式为y=kx+b(k≠0),
将(40,125),(100,215)代入,得:,
解得:,
∴y=x+65(40≤x≤100),
∴当A,B两市接种人数恰好相同时,x+65=x2+x,
解得:x1=﹣25(舍去),x2=52,
答:第52天接种完成后,A,B两市接种人数恰好相同.
17.解:(1)设y=kx+b(k≠0),
由题意得:,
解得:,
∴y与x的函数关系式为:y=﹣10x+530;
故答案为:y=﹣10x+530;
(2)①当x=45时,m=﹣45×10+530=80,
该商场购进玩具单价为:30﹣(2300÷230)=20(元),
故答案为:80;20.
②由题意得:
w=(x﹣20)?y,
=(x﹣20)(﹣10x+530),
=﹣10x2+730x﹣10600,
=﹣10(x﹣36.5)2+2722.5,
∵﹣10<0,
∴当x=36.5时,y有最大值2722.5,
∴w与x的函数关系式为w=﹣10x2+730x﹣10600,
当销售单价x定为36.5元时,月销售利润最大,最大利润是2722.5元.
(3)由题意得:2340=(﹣10x+530)(x﹣20﹣n)=﹣10(x﹣53)(x﹣20﹣n),
函数的对称轴为:x==,
∵0<n≤7,n为整数,
∴20+n<53,且20<20+n≤27,
∴≤40,
∵﹣10<0,
∴在对称轴的右侧,w随x的增大而减小,
∵x≥40,
则函数在x=40处取得最大值,将x=40代入函数表达式得:
2340=(﹣10x+530)(x﹣20﹣n),解得:n=2.
故答案为:2.
18.解:根据题意得:
w=(﹣2x+40)(x﹣10)
=﹣2x2+60x﹣400
=﹣2(x﹣15)2+50,
∴当x=15时,w取得最大值,最大值为50.
∵1<15<19,
∴x=15符合题意.
∴当该商品的销售单价定为15元/件时,日销售利润最大,最大利润是50元.
19.解:(1)y=x(36﹣2x)
=﹣2x2+36x,
∵0<36﹣2x≤18,
∴9≤x<18.
∴y与x之间的函数关系式为y=﹣2x2+36x(9≤x<18);
(2)由题意得:﹣2x2+36x=160m2,
解得x1=8,x2=10,
∵9≤x<18,
∴x1=8不符合题意,
∴x=10;
(3)∵y=﹣2x2+36x
=﹣2(x﹣9)2+162,
∴当x=9时,y有最大值162.
∴墙长36﹣2x=36﹣18=18(m),
∴矩形ABCD空地的面积最大为162m2时,利用的墙长是18m.
20.解:(1)设该商品每天的销售量y(件)与销售单价x(元)之间的函数关系式为y=kx+b,
将点(3,100)、(40,80)代入一次函数关系式得:
,
解得:.
∴函数关系式为y=﹣2x+160;
(2)由题意得:(x﹣30)(﹣2x+160)=800,
整理得:x2﹣110x+2800=0,
解得:x1=40,x2=70.
∵单价不低于成本价,且不高于50元销售,
∴x2=70不符合题意,舍去.
∴销售单价定为40元时,每天的销售利润为800元;
(3)由题意得:
w=(x﹣30)(﹣2x+160)
=﹣2(x﹣55)2+1250,
∵﹣2<0,抛物线开口向下,
∴当x<55时,w随x的增大而增大,
∵30≤x≤50,
∴当x=50时,w有最大值,此时w=﹣2(50﹣55)2+1250=1200.
∴销售单价定为50元时,才能使销售该商品每天获得的利润w(元)最大,最大利润是1200元.
21.解:(1)当2<x≤5时,y=600;
当5<x≤10时,设y=kx+b(k≠0),把(5,600),(10,400)代入得:
,
解得,
∴y=﹣40x+800,
∴y与x之间的函数关系式为:
y=;
(2)设每天的销售利润为w元,
当2<x≤5时,
w=600(x﹣2)=600x﹣1200,
当x=5时,wmax=600×5﹣1200=1800(元);
当5<x≤10时,
w=(﹣40x+800)(x﹣2)
=﹣40(x﹣11)2+3240,
当x=10时,
wmax=﹣40×1+3240=3200(元).
综上所述,销售单价x为10元时,每天的销售利润最大,最大利润是3200元.
22.解:(1)由题意得:
w=(x﹣20)?y
=(x﹣20)(﹣10x+500)
=﹣10x2+700x﹣10000.
∵每件的利润不高于成本价的60%.
∴20≤x≤20(1+60%),
∴20≤x≤32,
∴w=﹣10x2+700x﹣10000(20≤x≤32).
(2)∵w=﹣10x2+700x﹣10000(20≤x≤32),
∴对称轴为直线x=﹣=35,
又∵a=﹣10<0,
∴抛物线开口向下,
∴当20≤x≤32时,w随x的增大而增大,
∴当x=32时,w有最大值,最大值为﹣10×322+700×32﹣10000=2160(元).
∴当销售单价定为32元时,每月可获得最大利润,每月的最大利润是2160元.
23.(1)设抛物线的解析式为y=a(x﹣1)2﹣
由于抛物线经过点B(﹣2,0),
∴a(﹣2﹣1)2﹣=0,
解得:a=,
∴二次函数的解析式为y=x2﹣x﹣4.
(2)易知:D点坐标为(0,﹣4),
可求得直线AD的函数解析式为y=﹣x﹣4,
由于BP∥AD,故可设直线BP的函数解析式为:
y=﹣x+b,
又BP经过点B,得:﹣×(﹣2)+b=0,
解得:b=﹣1,
从而BP的解析式为y=﹣x﹣1,
∴该直线与抛物线的交点P的坐标为(3,﹣),
又可求得点C(4,0),
∴PC==,
过点M作ME∥x轴交直线BP于点E,
设点M的坐标为(m,n),则点E的纵坐标为n,
∴点E的横坐标为﹣2n﹣2,
∴ME=﹣2n﹣2﹣m,
∵ME∥BC,MN∥PC,
∴∠E=∠PBC,∠MNE=∠BPC,
MN=PC=﹣(m+2n+2)
=﹣(m+m2﹣2m﹣8+2)
=﹣(m﹣)2+,
∴当m=时,MN有最大值,
(3)设点Q的坐标为(a,b),过点Q作QM∥x轴,过点B作BM∥y轴,交QM于点M,过点F作FN∥y轴交QM于点N,过点E作EK∥x轴交BM于点K,
∴△BMQ≌△QNF≌△EKB,
∴NF=KB=MQ=a+2,QN=EK=BM=b
∴点F的坐标为(a﹣b,a+b+2),
点E的坐标为(﹣2﹣b,a+2),
当点F在抛物线的对称轴上时,a﹣b=1,
∴a﹣(a2﹣a﹣4)=1,
解得:a=2﹣(舍去正值),
得点Q的坐标为(2﹣,1﹣),
当点E在抛物线的对称轴上时,﹣2﹣b=1,
∴﹣2﹣(a2﹣a﹣4)=1,
解得:a=1﹣(舍去正值),
得点Q的坐标为(1﹣,﹣3).
24.解:(1)抛物线y=x2﹣x﹣与x轴交于点A和点B,与y轴交于点C,
令x=0,则y=﹣;令y=0,则y=(x+1)(x﹣3)=0,则x=﹣1或x=3;
∴A(﹣1,0),B(3,0),C(0,﹣),
经过点C的直线l与抛物线交于另一点E(4,a),
∴a=×42﹣×4﹣,即a=,
∴E(4,),
设直线CE的解析式为:y=kx+b,
∴,解得,
∴直线CE的解析式为:y=x﹣;
(2)∵直线CE与x轴交于点F,
∴F(,0),
如图,过点P作x轴的垂线,交CE于点M,
设点P的横坐标为m,
∴P(m,m2﹣m﹣),M(m,m﹣),
∴MP=m﹣﹣(m2﹣m﹣)=﹣m2+m,
∴S△PCF=(xF﹣xC)?MP=××(﹣m2+m)=﹣(m﹣2)2+,
∴当m=2时,S△PCF的最大值为,此时P(2,﹣).
(3)在直线QH上是否存在点G,使得△DQG为等腰三角形,理由如下:
∵抛物线y=x2﹣x﹣=(x﹣1)2﹣,
∴D(1,0),Q(1,﹣),
∴DQ=,tan∠OCD=,
∴∠OCD=30°,
抛物线沿射线CD平移得到新抛物线y′,y′经过点D,如图,
则y′的顶点为点H(2,﹣),∠DQH=∠OCD=30°,
∴直线QH的解析式为y=x﹣.
①当DG1=DQ=时,如图所示,过点G1作G1I⊥DQ于点I,
此时∠G1DI=60°,
∴DI=DG1=,G1I=DI=2,
∴G1(3,);
②当QG1=QD=时,如图所示,过点G2作G2T⊥DQ于点T,过点G3作G3S⊥DQ于点S,
∴G2T=QG2=,TQ=G2T=2,
∴G2(1+,2﹣);
同理可得,G3S=,SQ=2,
∴G3(1﹣,﹣2﹣);
③当GD=GQ时,如图所示,此时点G4为DQ的中垂线与直线QH的交点,
∴G4的纵坐标为﹣,
∴G4(,﹣);
综上,点G的坐标为:(3,);(1+,2﹣);(1﹣,﹣2﹣);(,﹣).
25.解:(1)以抛物线的顶点为原点,抛物线的对称轴为y轴建立平面直角坐标系,如图所示:
设抛物线解析式为y=ax2,点D的坐标为D(5,m),则B(10,m﹣3),
由抛物线经过点D和点B,可得:,
解得:,
∴抛物线的解析式为y=﹣x2;
(2)由(1)可得CD距拱顶的距离为1m,水位以每小时0.2m的速度上升,从警戒线开始,到达拱顶的时间为=5(小时).
∴从警戒线开始,再持续5小时就能到达拱桥的拱顶.
26.解:(1)设y与x满足的函数表达式为y=kx+b(k≠0),
将(24,42),(30,24)分别代入,得:
,
解得:,
∴y与x满足的函数表达式为y=﹣3x+114.
(2)由题意得:
W=(x﹣20)?y
=(x﹣20)(﹣3x+114)
=﹣3x2+174x﹣2280
=﹣3(x﹣29)2+243.
∴当x=29时,W有最大值243.
∴销售价格定为29元/件时,才能使每天获得的利润W最大.
27.解:(1)①当2≤x<8时,设直线AB解析式为:y=kx+b,
将A(2,12)、B(8,6)代入得:
,
解得,
∴y=﹣x+14(2≤x<8);
②当x≥8时,y=6.
∴A类杨梅平均销售价格y与销售量x之间的函数关系式为:y=;
(2)设销售A类杨梅x吨,则销售B类杨梅(20﹣x)吨.
当2≤x<8时,
wA=x(﹣x+14)﹣x=﹣x2+13x;
wB=9(20﹣x)﹣[12+3(20﹣x)]=108﹣6x,
∴w=wA+wB﹣3×20
=(﹣x2+13x)+(108﹣6x)﹣60
=﹣x2+7x+48;
当x≥8时,
wA=6x﹣x=5x;
wB=9(20﹣x)﹣[12+3(20﹣x)]=108﹣6x,
∴w=wA+wB﹣3×20
=(5x)+(108﹣6x)﹣60
=﹣x+48.
∴w关于x的函数关系式为:w=;
(3)设该公司用132万元共购买了m吨杨梅,其中A类杨梅为x吨,B类杨梅为(m﹣x)吨,则购买费用为3m万元,A类杨梅加工成本为x万元,B类杨梅加工成本为[12+3(m﹣x)]万元,
∴3m+x+[12+3(m﹣x)]=132,
化简得:x=3m﹣60.
①当2≤x<8时,
wA=x(﹣x+14)﹣x=﹣x2+13x;
wB=9(m﹣x)﹣[12+3(m﹣x)]=6m﹣6x﹣12,
∴w=wA+wB﹣3×m
=(﹣x2+13x)+(6m﹣6x﹣12)﹣3m
=﹣x2+7x+3m﹣12.
将3m=x+60代入得:w=﹣x2+8x+48=﹣(x﹣4)2+64,
∴当x=4时,有最大毛利润64万元,
此时m=,m﹣x=;
②当x≥8时,wA=6x﹣x=5x;
wB=9(m﹣x)﹣[12+3(m﹣x)]=6m﹣6x﹣12,
∴w=wA+wB﹣3×m
=(5x)+(6m﹣6x﹣12)﹣3m
=﹣x+3m﹣12.
将3m=x+60代入得:w=48,
∴当x>8时,有最大毛利润48万元.
综上所述,购买杨梅共吨,其中A类杨梅4吨,B类吨,公司能够获得最大毛利润,最大毛利润为64万元.
28.解:(1)设y与x之间的函数解析式为y=ax2+bx+c,
根据题意得:,
解得:,
∴y=﹣x2+16x+34;
(2)令y=0,得:﹣x2+16x+34=0,
解得:x1=﹣2(舍),x2=34.;
∴从7:00开始,需要34分钟校门口的学生才能全部进校;
(3)设第x分钟时的排队等待人数为w人,
由题意得:w=y﹣2x
=﹣x2+14x+34,
当x=30时,w=4>0.
∴7点30分时所有学生不能全部完成进校.
29.解:(1)设AB长为x米,花圃面积为y平方米,由题意得:
y=x(80﹣2x)
=﹣2x2+80x
=﹣2(x﹣20)2+800,
∴对称轴为x=20,
由题意得:
,
解得22≤x<40.
∵﹣2<0,抛物线开口向下,
∴当x>20时,y随x的增大而减小,
∴当x=22时,y有最大值,最大值为792.
∴当AB长为22米时所围成的花圃面积最大,最大值是792平方米.
(2)由(1)知y=﹣2x2+80x
令y=350得:350=﹣2x2+80x,
解得:x1=5,x235,
∵22≤x<40,
∴x=35.
∴当花圃的面积为350平方米时,AB长为35米.
30.解:(1)设A型保鲜货车载重量为x吨,B型保鲜货车载重量为y吨,
由题意得:,
解之得:,
答:A型保鲜货车的满载重量为2吨,B型保鲜货车的满载重量为3吨.
(2)设储存m天之后,获得利润为w万元,根据题得:
w=(0.9+0.1m)(40﹣0.5m)﹣40×0.8﹣40×0.08m=36﹣0.45m+4m﹣0.05m2﹣40×0.8﹣40×0.08m=﹣0.05m2+0.35m+4=﹣0.05(m2﹣7m)+4=﹣0.05(m﹣3.5)2+4.6125,
∵a=﹣0.05<0,
∴w有最大值,
∵对称轴为m=3.5,且0≤m≤20,m为整数,
∴当m=3或4时,wmax=﹣0.05×0.25+4.6125=4.6
答:保鲜储存至第3或4天时,利润最大为4.6万元.
31.解:(1)意义是:购买不超过15本此种笔记本时售价为5元/本.
故答案为:购买不超过15本此种笔记本时售价为5元/本;
(2)①当0<x≤15时,y与x之间的函数关系式y=5,
②当15<x≤25时,设=kx+b根据题意得,
解得.
∴y与x之间的函数关系式y=﹣0.1x+6.5.
③当x>25时,y与x之间的函数关系式为:y=4.
综上,y与x之间的函数关系式为:y=;
(3)由题意得:
W=(﹣0.1x+6.5﹣3)x
=﹣0.1x2+3.5x
∵﹣0.1<0,对称轴x=17.5,且x为整数,
∴当x=17或18时,W有最大值30.6元,
∴当小明购买17或18本时,该文具批发部所获的利润最大,最大利润是30.6元.
32.解:(1)设y=kx+b(k≠0,b为常数),
将点(60,140),(70,120)代入,得,
解得,
∴y与x的函数关系式为y=﹣2x+260;
(2)由题意得:(x﹣50)(﹣2x+260)=2400,
化简得:x2﹣180x+7700=0,
解得:x1=70,x2=110,
∵50×(1+90%)=95,且110>95,
∴x2=110(舍去),
∴x=70.
∴销售单价应定为70元;
(3)设每天获得的利润为W元,由题意得:
W=(x﹣50)(﹣2x+260)
=﹣2(x﹣90)2+3200,
∵a=﹣2,抛物线开口向下,
∴W有最大值,当x=90时,W最大值=3200.
∴销售单价为90元时,每天获得的利润最大,最大利润是3200元.
33.解:(1)∵y与x满足一次函数的关系,
∴设y=kx+b(k≠0),
将x=12,y=1200;x=13,y=1100代入得:
,
解得:,
∴y与x的函数关系式为:y=﹣100x+2400;
(2)设线上和线下月利润总和为W元,
则W=400(x﹣2﹣10)+y(x﹣10)
=400x﹣4800+(﹣100x+2400)(x﹣10)
=﹣100(x﹣19)2+7300,
∴当x为19时,线上和线下月利润总和达到最大.
34.解:(1)(x﹣20)(﹣x+50)=﹣x2+70x﹣1000,
∴每天获得的利润为(﹣x2+70x﹣1000)元;
(2)设每天可获得的利润为w,由题意得:
w=﹣x2+70x﹣1000
=﹣(x2﹣70x)﹣1000
=﹣(x2﹣70x+352﹣352)﹣1000
=﹣(x﹣35)2+225,
∴当x=35时,w有最大值225.
∴当每千克售价为35元时,每天可获得最大利润;
(3)由题意得:﹣(x﹣35)2+225=200,
∴(x﹣35)2=25,
∵平方等于25的数是5或﹣5,
∴x﹣35=5,或x﹣35=﹣5,
∴x=40或x=30,
∵30<x<50,
∴x=40.
∴若每天获得利润200元,那么每千克售价应定为40元.
35.解:(1)将A、C的坐标(﹣3,0)、(0,2)代入函数式且对称轴为x=﹣2,,
∴,
∴抛物线的解析式为:y=x2+x+2.
(2)由点A、C的坐标(﹣3,0)、(0,2)可知,直线AC为:y=x+2,
∵DE∥AC,
kDE=kAC,
∴kDE=,
∵D与C关于
x=﹣2对称,
∴D(﹣4,2),
∴DE直线为:y=,
联立,,
∴,
∴E的横坐标为1,
代入可得,y=,
∴E(1,),
连接DC,
∵DE∥AC,
∴S△DEG=S△DEC,
令lDE的x=0,
∴y=,
∴M(0,),
∴S△DEC=S△DCM+S△ECM=,
∴S△DEG=,
∵S△EFG=S△DEF﹣S△DEG=S△DEF﹣,
∴△EFG的面积最大,
作FK⊥x轴,交DE于K,
∵F在抛物线上,
设F为(t,),
∴K(t,),
∴S△DEF=S△DFK+S△EFK=(xE﹣xD)(yK﹣﹣yF)=(﹣)=﹣,
∴当t=﹣时,三角形DEF面积最大,面积为:,
∴当F(﹣,﹣)时,S△EFG最大为.
(3)假设存在,
∵C(0,2),F(﹣,﹣),
∴设Q(m,m2+m+2),P(xP,yP),
∵P、Q、F、C为顶点的四边形为矩形,
∴m≠0,m,
∴kCF==,
∴直线QF:kQF==(m+),
①当P、Q、F、C的四边形以CF为对角线,
,
∴kQC?kQF=﹣1,
∴﹣=xP+m,
,
∴4m2+2m+49=0,
∵△=262﹣4×4×49=﹣105<0,
∴无解,此时不存在.
②以CQ为对角线,
∴,
∴kCF?kQF=﹣1,
∴+xP,
,
∴,
∴,
∴.
③以CP为对角线,
,
∴kCF?kQC=﹣1,
∴x,
∴,
∴,
∴,
∴P(﹣,),
∴综上,P
为(﹣,)或(﹣,).
36.解:(1)∵抛物线过点O(0,0)、A(2m,0),
∴设抛物线的解析式为y=a(x﹣0)(x﹣2m),
∵抛物线顶点为P(m,m),
∴将点P坐标代入得:a=﹣,
∴抛物线的解析式为y=﹣x(x﹣2m);
(2)∵P(m,m),对称轴直线l⊥x轴,
∴OC=CP=m,
∴△OPC是等腰直角三角形,
∴OP=OC=m,∠OPC=45°,
∵OP=MN,
∴MN=2OP=2m,
∵M、N关于点P对称,
∴MP=NP=MN=m=OP,
∴点O、M、N三点都在以点P为圆心、OP为半径的圆上,如图
∴∠MON=90°,
∵OC=CA=m,∠OCN=∠CAN=90°,CN=CN,
∴△OCN≌△CAN,
∴∠ONC=∠ANC,
∵∠ONC=∠OPC=22.5°,
∴∠ONB=2∠OPC=45°,
∴△NOB是等腰直角三角形;
②设PM=PN=d,
∵点P坐标为(m,m),
∴M的坐标为(m,m﹣d),
∴直线OM的解析式为y=,
联立抛物线解析式得:x1=0,x2=m+d,
∴点B坐标为(m+d,),
同理点N(m,m+d)可得直线AN的解析式为y=﹣,
令x=m+d代入直线AN解析式得y=,
∴点B在AN上,即点A、B、N三点共线,
由(2)得△OCN≌△CAN,
∴∠ONM=∠CAN=∠BNM.
37.解:(1)令x=0代入y=﹣3x+3,
∴y=3,
∴B(0,3),
把B(0,3)代入y=ax2﹣2ax﹣3a,
∴3=﹣3a,
∴a=﹣1,
∴二次函数解析式为:y=﹣x2+2x+3;
(2)令y=0代入y=﹣x2+2x+3,
∴0=﹣x2+2x+3,
∴x=﹣1或3,
∴抛物线与x轴的交点横坐标为﹣1和3,
∵M在抛物线上,且在第一象限内,
∴0<m<3,
令y=0代入y=﹣3x+3,
∴x=1,
∴A的坐标为(1,0),
由题意知:M的坐标为(m,﹣m2+2m+3),
S=S四边形OAMB﹣S△AOB
=S△OBM+S△OAM﹣S△AOB
=×m×3+×1×(﹣m2+2m+3)﹣×1×3
=﹣(m﹣)2+,
∴当m=时,S取得最大值.
(3)由(2)可知:M′的坐标为(,);
②过点M′作直线l1∥l′,过点B作BF⊥l1于点F,
根据题意知:d1+d2=BF,
此时只要求出BF的最大值即可,
∵∠BFM′=90°,
∴点F在以BM′为直径的圆上,
设直线AM′与该圆相交于点H,
∵点C在线段BM′上,
∴F在优弧上,
∴当F与M′重合时,
BF可取得最大值,
此时BM′⊥l1,
∵A(1,0),B(0,3),M′(,),
∴由勾股定理可求得:AB=,M′B=,M′A=,
过点M′作M′G⊥AB于点G,
设BG=x,
∴由勾股定理可得:M′B2﹣BG2=M′A2﹣AG2,
∴﹣(﹣x)2=﹣x2,
∴x=,
∵l1∥l′,
∴∠BCA=90°,
∠BAC=45°;
方法二:过B点作BD垂直于l′于D点,过M′点作M′E垂直于l′于E点,则BD=d1,ME=d2,
∵S△ABM′=×AC×(d1+d2)
当d1+d2取得最大值时,AC应该取得最小值,当AC⊥BM′时取得最小值.
根据B(0,3)和M′(,)可得BM′=,
∵S△ABM=×AC×BM′=,
∴AC=,
当AC⊥BM′时,
∴∠BAC=45°.
38.解:(1)在y=ax2+bx﹣3中,当x=0时,y=﹣3.
∴点C(0,﹣3).
∵抛物线顶点D(1,﹣4).
∴设抛物线为:y=a(x﹣1)2﹣4.
代点C(0,﹣3)得:﹣3=a﹣4.
∴a=1.
∴抛物线为:y=(x﹣1)2﹣4=x2﹣2x﹣3.
当y=0时,x2﹣2x﹣3=0.
解得x=﹣1或x=3.
∴B(3,0).
代入y=﹣x+c得:0=﹣+c.
∴c=.
(2)分两种情况:
①当AD=DN时,根据抛物线的对称性知点B与点N重合,故N(3,0).
②当NA=ND时,点N在线段AD的垂直平分线上.
∵A(﹣1,0),D(1,﹣4).
∴AD的中点F的坐标是(,),即F(0,﹣2).
设直线AD的解析式为:y=kx+b,则:
,解得k=﹣2,b=﹣2.
∴直线AD:y=﹣2x﹣2.
设直线AD的垂直平分线为FN的表达式为:y=x+b.
代入F(0,﹣2)得:b=﹣2.
∴直线NF:y=x﹣2.
由得:或.
∵点N在y轴右侧的抛物线上.
∴N(,).
综上可知,点N的坐标为(3,0)或(,).
(3)点F的横坐标是.
如图:
在BE上选一点F,在OB上选一点M,使得FM=MB,则∠FMG=2∠ABE.
在OB上点M的左侧取一点G,使得FG=FM,则∠EFG=∠FGM+∠ABE=3∠ABE.
移动点F,当GH=2FG时,点F即为所求.
过点F作FP⊥x轴于点P,过点H作HQ⊥x轴于点Q,则GP=PM
设F(m,﹣m+),则OP=m,FP=﹣m+.
∴HQ=2FP=﹣m+3.
易得PB=2FP.∴FM=BM=PB﹣PM=2FP﹣PM.
由勾股定理得:FP2+PM2=FM2,即FP2+PM2=(2FP﹣PM)2.
∴PM=﹣m+=GP.
OG=OP﹣GP=m﹣.
GQ=2GP=﹣m+.
∴OQ=GQ﹣OG=﹣m+.
∴H(m﹣,m﹣3).
易求直线AD的表达式为:y=﹣2x﹣2,
将H代入得:m﹣3=﹣2(m﹣)﹣2.
解得:m=.
故点F的横坐标为:.
39.解:(1)∵抛物线C:y=(x﹣2)2向下平移6个单位长度得到抛物线C1,
∴C1:y=(x﹣2)2﹣6,
∵抛物线C1向左平移2个单位长度得到抛物线C2,
∴C2:y=(x﹣2+2)2﹣6,
即y=x2﹣6,
(2)过点A作AC⊥x轴于点C,过点B作BD⊥AC于点D,如图所示:
设A点坐标为(a,(a﹣2)2﹣6),
∴C点坐标为(a,0),
∵C1的对称轴x=2,
∴OC=BD=a﹣2,AC=|(a﹣2)2﹣6|,
∵∠BAO=∠ACO=90°,
∠BAD+∠OAC=∠OAC+∠AOC=90°,
∴∠BAD=∠AOC,
∵AB=OA,∠ADB=∠OCA,
∴△ABD≌△OAC(AAS),
∴BD=AC,
∴a﹣2=|(a﹣2)2﹣6|,
解得,a=4,或a=﹣1,或a=0,或a=5,
∵A点在第一象限,
∴a=4或a=5,
∴A(4,﹣2)(舍弃)或(5,3),
∴A(5,3).
(3)把y=kx代入y=x2﹣6中得,x2﹣kx﹣6=0,
∴xE+xF==k,
∴M(),
将y=x代入y=x2﹣6,中得x2+x﹣6=0,
∴xG+xH=,
∴N(),
设MN的解析式为y=mx+n(m≠0),则
,
解得,,
∴直线MN的解析式为:y=x+2,
当x=0时,y=2,
∴直线MN:y=x+2经过定点(0,2),
即直线MN经过一个定点.
40.解:(1)将A(4,0),B(,)代入y=ax2+bx,
解方程组得a=﹣1,b=4,
∴抛物线的解析式为y=﹣x2+4x,
顶点G的坐标为:(2,4).
(2)设C(c,0),则E(c,﹣c2+4c),
∵点P是第三象限内抛物线上一点,
故可设P(t,﹣t2+4t),其中t<0,
设PE:y=kx+m,则,
解得:,
∴PE:y=(4﹣t﹣c)x+ct,
令x=0,得y=ct,即M(0,ct),
∴OC=c,OM=﹣ct,
∴MC∥ND.
(3)解方程组,
得:,,
∴Q(4﹣k,4k﹣k2),
根据O,G,Q坐标可求
OG=,
OQ=,
GQ=,
∵∠OQG=90°,
∴OQ2+GQ2=OG2,
即
(4﹣k)2+(4k﹣k2)2+(2﹣k)2+(4k﹣k2﹣4)2=20,
∴(k﹣4)2+k2(k﹣4)2+(k﹣2)2+(k﹣2)4=20,
令k﹣2=t,则(t﹣2)2+(t+2)2(t﹣2)2+t2+t4=20,
展开化简得t4﹣3t2﹣2t=0,
进行因式分解得t(t+1)2(t﹣2)=0,
∴t=0或者t=﹣1或t=2,
∴k=2或者k=1或k=4,
当k=2时,Q(2,4)与G重合,不符题意,舍去,
当k=1时,Q(3,3),符合题意,
当k=4时,Q(0,0)与原点重合,不符题意,舍去,
∴k=1.
41.解:(1)由y=0,得x2﹣4x+3=0,
解得,x1=1,x2=3,
∵点A在点B的左侧,
∴点A的坐标为(1,0),点B的坐标为(3,0),
由x=0,得y=3,
∴点C的坐标为(0,3).
(2)∵y=x2﹣4x+3=(x﹣2)2﹣1,
∴点D的坐标为(2,﹣1),抛物线的对称轴为直线x=2,
设M(2,m),m<﹣1,
由DM=﹣1﹣m,
∴OM2=m2+4,BM2=m2+1,
若BM=OM,则m2+4=m2+1,此方程无解,
若BM=OB,则9=m2+1,
解得m=﹣2或m=2(不合题意,舍去),
∴t=DM=2﹣1,
若OM=OB,则9=m2+4,
解得m=﹣或m=(不合题意,舍去),
∴t=DM=﹣1,
综上所述,当t=2﹣1或﹣1时,△OMB为等腰三角形;
(3)存在点P,使∠PBF被BA平分,
在y轴上取一点N(0,﹣),连接BN交抛物线于点P,则∠PBO=∠EBO,
设直线BN的解析式为y=kx﹣,
∴3k﹣=0,
解得,k=,
∴直线BN的解析式为:y=x﹣,
解方程:x2﹣4x+3=x﹣,
解得,x1=,x2=3(不合题意,舍去),
当x=时,y=﹣,
∴P(,﹣),
∴存在点P(,﹣),使得∠PBF被BA平分.
42.解:(1)由题意可得,,
解得,,
∴抛物线的解析式为:y=x2﹣2x﹣3;
(2)由(1)知,D(1,﹣4),C(0,﹣3),
∴E(1,4),
∵直线y=mx+1过点A(﹣1,0),
∴直线AF:y=x+1,
如图1,分别过点B,E作BG∥y轴,EH∥y轴,与AF交于点G,H,
∴S1=(xP﹣xA)?EH,S2=(xP﹣xA)?BG
∴=,
∵B(3,0),
∴G(3,4),BG=4,
∵E(1,4),
∴H(1,2),EH=2,
∴===,
∴的值是一个定值,这个定值为;
(3)如图2,过点B作BP⊥AC于点P,作∠BTC=∠BMC,过点O作ON∥BT交AC于点N,
∴∠ONC=∠BTC=∠BMC,
∴BT=BM,点P是点T,点M的中点,
∵A(﹣1,0),C(0,﹣3),
∴直线AC:y=﹣3x﹣3,
∵BP⊥AC,B(3,0),
∴直线BP:y=x﹣1,
联立,解得,
∴P(﹣,﹣),
∵B(3,0),D(1,﹣4),
∴直线BD:y=2x﹣6,
联立,解得,
∴M(,﹣),
∴由中点坐标公式可得,T(﹣,),
设直线BT的解析式为y=kx+b,
∴,解得,,
∴y=﹣x+,
∴直线ON的表达式为:y=﹣x,
联立,解得,
∴N(﹣,).
43.解:(1)∵AB∥OD,AB的解析式为y=x+2,
∴OD的解析式为y=x;C点的坐标为(0,2);
又∵DC⊥y轴;
∴D点的纵坐标为2,将y=2代入y=x中,得x=2,
∴D点的坐标为(2,2)
将点D(2,2)代入y=ax2(a>0)中,解得a=;
(2)由(1)知,抛物线的解析式为y=x2,
∴
解得,;
∴;;
∴由图可知点A坐标为,
点B的坐标为,
由图可知,直线AH过原点,
∴设AH的解析式为y=kx,将A点坐标代入,
解得k=;
∴,
又∵BG⊥x轴交x轴于点G,BG的延长线交AO的延长线于点H,
∴点G的坐标为()点H的横坐标为,
将点H横坐标代到y=x中得y=﹣2,
∴点H的坐标为();
∴BH=BG+GH=;
设AG所在直线的解析式为y1=k1x+b,代入A、G两点的坐标得:
解得:k1=,b=;
∴y1=x+;
∴OK=;
∴OK?BH==4.
(3)∵a=1,
∴设平移后抛物线的解析式为y=x2+bx+c,
将A(﹣1,0),B(2,0)两点代入可得b=﹣1,c=﹣2;
∴y=x2﹣x﹣2;
设点P的坐标为(0,e)
∴将点A、P坐标代入可得AM所在直线的解析式为yAM=ex+e;
将点B、P坐标代入可得BN所在直线的解析式为yBN=﹣x+e;
又∵N、M在抛物线上,
∴
解得xM=e+2,∴
解得,∴;
∵AB=3,
∴S3=S△APB=?AB?OP=;
S1=S△PNA=S△NAB﹣S△APB
=
=;
S2=S△PMB=S△MAB﹣S△APB
=
=
代入得
e2=13(e>0)
∴e=,
∴P(0,).
一、选择题
1.如图,抛物线y=x+2交x轴于点A,B,交y轴于点C,当△ABC纸片上的点C沿着此抛物线运动时,则△ABC纸片随之也跟着水平移动,设纸片上BC的中点M坐标为(m,n),在此运动过程中,n与m的关系式是( )
A.n=(m﹣)2﹣
B.n=(m﹣)2
C.n=(m﹣)2﹣
D.n=(m﹣)2﹣
2.苏州市“东方之门”是由两栋超高层建筑组成的双塔连体建筑,“门”的造型是东方之门的立意基础,“门”的内侧曲线呈抛物线型,如图1,两栋建筑第八层由一条长60m的连桥连接,在该抛物线两侧距连桥150m处各有一窗户,两窗户的水平距离为30m,如图2,则此抛物线顶端O到连桥AB距离为( )
A.180m
B.200m
C.220m
D.240m
3.如图,直线y=与y轴交于点A,与直线y=﹣交于点B,以AB为边向右作菱形ABCD,点C恰与原点O重合,抛物线y=(x﹣h)2+k的顶点在直线y=﹣上移动.若抛物线与菱形的边AB、BC都有公共点,则h的取值范围是( )
A.﹣2
B.﹣2≤h≤1
C.﹣1
D.﹣1
4.为测量某地温度变化情况,记录了一段时间的温度.一段时间内,温度y与时间t的函数关系满足y=﹣t2+12t+2,当4≤t≤8时,该地区的最高温度是( )
A.38℃
B.37℃
C.36℃
D.34℃
5.如图1,一个移动喷灌架喷射出的水流可以近似地看成抛物线.图2是喷灌架为一坡地草坪喷水的平面示意图,喷水头的高度(喷水头距喷灌架底部的距离)是1米.当喷射出的水流距离喷水头20米时,达到最大高度11米,现将喷灌架置于坡度为1:10的坡地底部点O处,草坡上距离O的水平距离为30米处有一棵高度约为2.3米的石榴树AB,因为刚刚被喷洒了农药,近期不能被喷灌.下列说法正确的是( )
A.水流运行轨迹满足函数y=﹣x2﹣x+1
B.水流喷射的最远水平距离是40米
C.喷射出的水流与坡面OA之间的最大铅直高度是9.1米
D.若将喷灌架向后移动7米,可以避开对这棵石榴树的喷灌
6.如图,Rt△OAB的顶点A(﹣2,4)在抛物线y=ax2上,将Rt△OAB绕点O顺时针旋转90°,得到△OCD,边CD与该抛物线交于点P,则点P的坐标为( )
(,)
B.(2,2)
C.(,2)
D.(2,)
7.如图,在平面直角坐标系中,抛物线y=x2+bx+c与x轴交于A、B两点,点A在x轴的负半轴,点B在x轴的正半轴,与y轴交于点C,且CO=2AO,CO=BO,AB=3.则下列判断中正确的是( )
A.此抛物线的解析式为y=x2+x﹣2
B.当x>0时,y随着x的增大而增大
C.此抛物线与直线y=只有一个交点
D.在此抛物线上的某点M,使△MAB的面积等于4,这样的点共有三个
二、填空题
8.用一根长为20cm的铁丝围成一个矩形,该矩形面积的最大值是
cm2.
9.京剧作为一门中国文化的传承艺术,常常受到外国友人的青睐.如图,在平面直角坐标系xOy中,某脸谱轮廓可以近似地看成是一个半圆与抛物线的一部分组合成的封闭图形,记作图形G.点A,B,C,D分别是图形G与坐标轴的交点,已知点D的坐标为(0,﹣3),AB为半圆的直径,且AB=4,半圆圆心M的坐标为(1,0).关于图形G给出下列四个结论,其中正确的是
(填序号).
①图形G关于直线x=1对称;②线段CD的长为3+;
③图形G围成区域内(不含边界)恰有12个整点(即横、纵坐标均为整数的点);
④当﹣4≤a≤2时,直线y=a与图形G有两个公共点.
10.如图,直线y=kx+b交坐标轴于A、B两点,交抛物线y=ax2于点C(4,3),且C是线段AB的中点,抛物线上另有位于第一象限内的一点P,过P的直线y=k′x+b′交坐标轴于D、E两点,且P恰好是线段DE的中点,若△AOB∽△DOE,则P点的坐标是
.
11.如图1,AO,BC是两根垂直于地面的立柱,且长度相等.在两根立柱之间悬挂着一根绳子,如图2建立坐标系,绳子形如抛物线y=﹣x+4的图象.因实际需要,在OA与BC间用一根高为2.5m的立柱MN将绳子撑起,若立柱MN到OA的水平距离为3m,MN左侧抛物线的最低点D与MN的水平距离为1m,则点D到地面的距离为
.
12.如图1是某校园运动场主席台及遮阳棚,其侧面结构示意图如图2所示.主席台(矩形ABCD)高AD=2米,直杆DE=5米,斜拉杆EG,EH起稳固作用,点H处装有一射灯.遮阳棚边缘曲线FHG可近似看成抛物线的一部分,G为抛物线的最高点且位于主席台边缘BC的正上方,若点E,H,C在同一直线上,且DF=1米,EG=4米,∠AEG=60°,则射灯H离地面的高度为
米.
13.如图,分别过点Pi(i,0)(i=1、2、…、n)作x轴的垂线,交的图象于点Ai,交直线于点Bi.则=
.
已知,直线y=x+2与y轴交于点A,与直线y=﹣x交于点B,以AB为边向右作菱形ABCD,点C恰与原点O重合,抛物线y=(x﹣h)2+k的顶点在直线y=﹣x上移动.若抛物线与菱形的边AB、BC都有公共点,则h的取值范围是
.
三、解答题
15.有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为4m,跨度为10m.现将它的图形放在如图所示的直角坐标系中.求这条抛物线的解析式.
16.A市计划对本市215万人接种新冠疫苗,在前期完成5万人接种后,又花了100天时间接种了剩下的210万人.在这100天中,该市的接种时间和接种人数的关系如图所示,已知这100天中该市前a天每天接种人数是a天后每天接种人数的2倍.
(1)求a的值;
(2)这100天中,B市的接种人数y(万人)与接种天数x(天)的关系为y=x2+x,
①请通过计算判断,第a天接种完成后,B市的接种人数是否超过A市?
②第几天接种完成后,A,B两市接种人数恰好相同?
17.商场购进一批儿童智力玩具,调查发现:该玩具的月销售量y(个)与销售单价x(元)之间满足一次函数关系,下表是销售单价与月销售量、月销售利润的对应值分别如下:
月销售单价x(元/个)
30
35
40
45
月销售量y(个)
230
180
130
m
月销售利润w(元)
2300
2700
2600
2000
(1)直接写出y与x的函数关系式
;
(2)根据以上信息填空:
①m=
;该商场购进玩具单价
元/个;
②求w与x的函数关系式,并求出当销售单价x定为多少时,月销售利润最大?
(3)由于生产玩具成本增加,商场购进玩具单价提高n元/个(0<n≤7,n为整数),商场规定每件玩具售价不能低于40元/个,该商场在今后的销售中,月销售量与售价仍然满足(1)中的函数关系.若月销售最大利润是2340元,则n的值是
.
18.某超市购进一种商品,进货单价为每件10元,在销售过程中超市按相关规定,销售单价不低于1元且不高于19元.如果该商品的销售单价x(单位:元/件)与日销售量y(单位:件)满足一次函数关系y=﹣2x+40,设该商品的日销售利润为w元,那么当该商品的销售单价x(元/件)定为多少时,日销售利润最大?最大利润是多少元?
19.某单位为响应市“创建全国文明城市”的号召,不断美化环境,拟在一块矩形空地上修建绿色植物园,其中一边靠墙,可利用的墙长不超过18m,另外三边由36m长的栅栏围成.设矩形ABCD空地中,垂直于墙的边AB=xm,面积为ym2(如图).
(1)求y与x之间的函数关系式,并求出自变量x的取值范围;
(2)若矩形空地的面积为160m2,求x的值;
(3)当矩形ABCD空地的面积最大时,利用的墙长是多少m;并求此时的最大面积.
20.2020年是脱贫攻坚的收官之年,老李在驻村干部的帮助下,利用网络平台进行“直播带货”,销售一批成本为每件30元的商品,按单价不低于成本价,且不高于50元销售,经调查发现,该商品每天的销售量y(件)与销售单价x(元)之间满足一次函数关系,部分数据如表所示.
销售单价x(元)
30
40
45
销售数量y(件)
100
80
70
(1)求该商品每天的销售量y(件)与销售单价x(元)之间的函数关系式;
(2)销售单价定为多少元时,每天的销售利润为800元?
(3)销售单价定为多少元时,才能使销售该商品每天获得的利润w(元)最大?最大利润是多少元?
21.2020年,新型冠状病毒肆虐,给人们的生活带来许多不便,网络销售成为这个时期最重要的一种销售方式.某乡镇农贸公司新开设了一家网店,销售当地农产品.其中一种当地特产在网上试销售,其成本为每千克2元.公司在试销售期间,调查发现,每天销售量y(kg)与销售单价x(元)满足如图所示的函数关系(其中2<x≤10).
(1)求y与x之间的函数关系式;
(2)销售单价x为多少元时,每天的销售利润最大?最大利润是多少元?
22.小明投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数:y=﹣10x+500,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.
(1)设小明每月获得利润为w(元),求每月获得利润w(元)与销售单价x(元)之间的函数关系式,并确定自变量x的取值范围.
(2)当销售单价定为多少元时,每月可获得最大利润?每月的最大利润是多少?
23.如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象与直线AB交于A、B两点,A(1,﹣),B(﹣2,0),其中点A是抛物线y=ax2+bx+c的顶点,交y轴于点D.
(1)求二次函数解析式;
(2)如图1,点P是第四象限抛物线上一点,且满足BP∥AD,抛物线交x轴于点C.M为直线AB下方抛物线上一点,过点M作PC平行线交BP于点N,求MN最大值;
(3)如图2,点Q是抛物线第三象限上一点(不与点B、D重合),连接BQ,以BQ为边作正方形BEFQ,当顶点E或F恰好落在抛物线对称轴上时,直接写出对应的Q点的坐标.
24.如图,抛物线y=x2﹣x﹣与x轴交于点A和点B,与y轴交于点C,经过点C的直线l与抛物线交于另一点E(4,a),抛物线的顶点为点Q,抛物线的对称轴与x轴交于点D.
(1)求直线CE的解析式.
(2)如图2,P为直线CE下方抛物线上一动点,直线CE与x轴交于点F,连接PF,PC.当△PCF的面积最大时,求点P的坐标及△PCF面积的最大值.
(3)如图3,连接CD,将(1)中抛物线沿射线CD平移得到新抛物线y′,y′经过点D,y′的顶点为点H,在直线QH上是否存在点G,使得△DQG为等腰三角形?若存在,求出点G的坐标.
25.如图所示,某河面上有一座抛物线形拱桥,桥下水面在正常水位AB时,宽为20m,若水位上升3m,水面就会达到警戒线CD,这时水面宽为10m.
(1)建立适当的平面直角坐标系并求出抛物线的解析式;
(2)若洪水到来时,水位以每小时0.2m的速度上升,从警戒线开始,再持续多少小时就能到达拱桥的拱顶?
26.商店购进一批单价为20元的T恤,经试验发现,每天销售件数y(件)与销售价格x(元/件)满足图中的一次函数关系.
(1)求y与x满足的函数表达式(不要求写出x的取值范围).
(2)在不积压且不考虑其他因素的情况下,销售价格定为多少元/件时,才能使每天获得的利润W最大?
27.某公司经营杨梅业务,以3万元/吨的价格向农户收购杨梅后,分拣成A、B两类,A类杨梅包装后直接销售;B类杨梅深加工后再销售A类杨梅的包装成本为1万元/吨,根据市场调查,它的平均销售价格y(单位:万元/吨)与销售数量x(x≥2)之间的函数关系如图;B类杨梅深加工总费用s(单位:万元)与加工数量t(单位:吨)之间的函数关系是s=12+3t,平均销售价格为9万元/吨.
(1)直接写出A类杨梅平均销售价格y与销售量x之间的函数关系式;
(2)第一次,该公司收购了20吨杨梅,其中A类杨梅有x吨,经营这批杨梅所获得的总利润为w万元,求w关于x的函数关系式;
(3)第二次,该公司准备投入132万元资金,请设计一种经营方案,使公司获得最大利润,并求出最大利润.
28.疫情期间,按照防疫要求,学生在进校时必须排队接受体温检测.某校统计了学生早晨到校情况,发现从7:00开始,在校门口的学生人数y(单位:人)随时间x(单位:分钟)的变化情况的图象是二次函数的一部分,如图所示.
(1)求y与x之间的函数解析式;
(2)从7:00开始,需要多少分钟校门口的学生才能全部进校?
(3)现学校通过调整校门口的入校通道,提高体温检测效率.经过调整,现在每分钟可以多通过2人,请问所有学生能够在7点30分完成进校吗?请说明理由.
29.为推进“世界著名花城”建设,深圳多个公园近期举办花展活动.某公园想用一段长为80米的篱笆,围成一个一边靠围墙的ABCD,墙长36米.
(1)当AB长为多少米时所围成的花圃面积最大?最大值是多少?
(2)当花圃的面积为350平方米时,AB长为多少米?
30.今年甲、乙两个果园的红心猕猴桃喜获丰收,已知甲果园的总产量为27吨,乙果园的总产量13吨,某果业公司租用A、B两种型号的保鲜货车去果园运输猕猴桃,甲果园需要A型保鲜货车满载猕猴桃运输6趟,同时需要B型保鲜货车满载猕猴桃运输5趟才能刚好运输完:乙果园需A型保鲜货车满载猕猴桃运输2趟,同时需要B型保鲜货车满载猕猴桃运输3趟刚好运输完.
(1)求A、B两种保鲜货车满载猕猴桃运输一趟分别是多少吨?
(2)果业公司收购该批猕猴桃的单价为0.8万元/吨,目前公司可以0.9万元/吨的价格售出,如果保鲜冷藏储存起来,旺市再销售以便获取最大利润,由于失水和腐烂,水果重量每天减少0.5吨,且每天需支付各种费用0.08万元/吨,而每天的价格会持续上涨0.1万元/吨、如果公司计划把该批猕猴桃最多保鲜冷藏储存20天,那么储存多少天后出售这批猕猴桃所获得的利润最大?最大利润是多少万元?
31.开学初,小明到文具批发部一次性购买某种笔记本,该文具批发部规定:这种笔记本售价y(元/本)与购买数量x(本)之间的函数关系如图所示.
(1)图中线段AB所表示的实际意义是
;
(2)请直接写出y与x之间的函数关系式;
(3)已知该文具批发部这种笔记本的进价是3元/本,若小明购买此种笔记本超过15本但不超过25本,那么小明购买多少本时,该文具批发部在这次买卖中所获的利润W(元)最大?最大利润是多少?
32.某景区纪念品超市以50元每个的价格新进一批工艺摆件,经过一段时间的销售发现日销量y(个)与单个售价x(元)之间的函数关系如图.(景区规定任何商品的利润率不得高于90%)
(1)根据图象,直接写出y与x的函数关系式;
(2)该超市要想每天获得2400元的销售利润,销售单价应定为多少元?
(3)销售单价为多少元时,每天获得的利润最大,最大利润是多少元?
33.在“新冠”疫情期间,全国人民“众志成城,同心抗疫”,某商家决定将一个月获得的利润全部捐赠给社区用于抗疫.已知商家购进一批产品,成本为10元/件,拟采取线上和线下两种方式进行销售.调查发现,线下的月销量y(单位:件)与线下售价x(单位:元/件,12≤x<24)满足一次函数的关系,部分数据如下表:
x(元/件)
12
13
14
15
16
y(件)
1200
1100
1000
900
800
(1)求y与x的函数关系式;
(2)若线上售价始终比线下每件便宜2元,且线上的月销量固定为400件,试问:当x为多少时,线上和线下月利润总和达到最大?
34.某种水果每千克进价20元,每千克售价x元(30<x<50),每天的销售量为(﹣x+50)千克.
(1)求每天获得利润(用含x的代数式表示);
(2)当每千克售价为多少元时,每天可获得最大利润?
(3)若每天获得利润200元,那么每千克售价应该定为多少元?
35.如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A、B
(点A在点B的左边),与y轴交于点C,点A、C的坐标分别为(﹣3,0)、(0,2),对称轴为直线x=﹣2.
(1)求抛物线的解析式;
(2)如图,点D与点C关于抛物线的对称轴对称,连接AC,过点D作DE∥AC交抛物线于点E,交y轴于点M.点F是直线AC下方抛物线上的一动点,连接DF交AC于点G,连接EG,求△EFG的面积的最大值以及取得最大值时点F的坐标;
(3)在(2)的条件下,点P为平面内一点,在抛物线上是否存在一点Q,是以点P、Q、F、C为顶点的四边形为矩形,如果存在,直接写出点P的坐标,如果不存在,说明理由.
36.如图,顶点为P(m,m)(m>0)的二次函数图象与x轴交于点A(2m,0),点B在该图象上,直线OB交二次函数图象对称轴l于点M,点M、N关于点P对称,连接BN、ON.
(1)求该二次函数的关系式(用含m的式子表示);
(2)若点B在对称轴l右侧的二次函数图象上运动,请解答下列问题:
①连接OP,当OP=MN时,请判断△NOB的形状,并说明理由.
②求证:∠BNM=∠ONM.
37.如图,直线l:y=﹣3x+3与x轴、y轴分别相交于A、B两点,抛物线y=ax2﹣2ax﹣3a(a<0)经过点B.
(1)求该抛物线的函数表达式;
(2)已知点M是抛物线上的一个动点,并且点M在第一象限内,连接AM、BM,设点M的横坐标为m,△ABM的面积为S,求S与m的函数表达式,并求出S的最大值;
(3)在(2)的条件下,当S取得最大值时,动点M相应的位置记为点M′.将直线l绕点A按顺时针方向旋转得到直线l′,当直线l′与直线AM′重合时停止旋转,在旋转过程中,直线l′与线段BM′交于点C,设点B、M′到直线l′的距离分别为d1、d2,当d1+d2最大时,求直线l′旋转的角度(即∠BAC的度数).
38.如图,已知抛物线y=ax2+bx﹣3(a≠0)与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,顶点D的坐标为(1,﹣4),连接AD.直线y=﹣x+c经过点B,且与y轴交于点E.
(1)求抛物线的解析式及c的值.
(2)点N为抛物线在y轴右侧的部分上一点,当△ADN是以DN为腰的等腰三角形时,求点N的坐标.
(3)点F为线段BE上一点,点G为线段OB上一点,连接FC,FG的延长线与线段AD交于点H,当∠EFG=3∠ABE,且GH=2FG时,直接写出点F的横坐标.
39.将抛物线C:y=(x﹣2)2向下平移6个单位长度得到抛物线C1,再将抛物线C1向左平移2个单位长度得到抛物线C2.
(1)直接写出抛物线C1,C2的解析式;
(2)如图(1),点A在抛物线C1(对称轴l右侧)上,点B在对称轴l上,△OAB是以OB为斜边的等腰直角三角形,求点A的坐标;
(3)如图(2),直线y=kx(k≠0,k为常数)与抛物线C2交于E,F两点,M为线段EF的中点;直线y=﹣x与抛物线C2交于G,H两点,N为线段GH的中点.求证:直线MN经过一个定点.
40.如图1,已知抛物线y=ax2+bx经过点A(4,0)、B(,).
(1)直接写出抛物线的解析式和顶点G的坐标;
(2)如图2,点C、D是线段OA上的两点(不含端点),过C、D分别作x轴的垂线,交抛物线于点E、F.设P是第三象限内抛物线上任意一点,连接PE和PF,分别交y轴于点M、N.求证:MC∥ND;
(3)如图3,直线y=kx(k>0)交抛物线于另一点于Q.当∠OQG=90°时,求k的值.
41.如图,在平面直角坐标系中,已知抛物线y=x2﹣4x+3与x轴交于A,B两点,点A在点B的左侧,与y轴交于点C,其顶点为点D,点E的坐标为(0,),该抛物线与BE交于另一点F,连接BC.
(1)求点A,B,C的坐标;
(2)动点M从点D出发,沿抛物线对称轴方向向下以每秒1个单位的速度运动,运动时间为t,连接OM,BM,当t为何值时,△OMB为等腰三角形?
(3)在x轴下方的抛物线上,是否存在点P,使得∠PBF被BA平分?若存在,请求出点P的坐标;若不存在,请说明理由.
42.如图1,已知抛物线y=x2+bx+c与x轴交于A(﹣1,0)、B(3,0)两点,与y轴交于点C,顶点为点D.
(1)求该抛物线的函数表达式;
(2)点E是点D关于x轴的对称点,经过点A的直线y=mx+1与该抛物线交于点F,点P是直线AF上的一个动点,连接AE、PE、PB,记△PAE的面积为S1,△PAB的面积为S2,那么的值是否是定值?如果是,请求出这个定值;如果不是,请说明理由.
(3)如图2,设直线AC与直线BD交于点M,点N是直线AC上一点,若∠ONC=∠BMC,求点N的坐标.
43.点A,B在抛物线y=ax2(a>0)上,AB交y轴于点C.
(1)过点C作DC⊥y轴交抛物线于点D,若AB∥OD,AB的解析式为y=x+2,求a的值;
(2)若点C(0,2)过点B作BG⊥x轴交x轴于点G,BG的延长线交AO的延长线于点H,连接AG交y轴于点K,求OK?BH的值;
(3)若a=1,将抛物线平移后交x轴于点A(﹣1,0),B(2,0)两点,点P为y轴正半轴上一点,AP,BP交抛物线于点M,N,设△PNA的面积为S1,△PMB的面积为S2,△PBA的面积为S3,若,求点P的坐标.
参考答案
1.解:∵抛物线y=x+2交x轴于点A,B,交y轴于点C,
∴点B的坐标为(4,0),点C的坐标为(0,2),
∴BC的中点M坐标为(,),即点M坐标为(2,1).
∵点C沿着此抛物线运动,点M也随之运动,点M的运动轨迹是抛物线,且经过(2,1),(6,﹣1)
∴设抛物线的解析式为y=x2+bx+c,
则有,解得
∴m,n满足,n=m2﹣m+8=(m﹣)2﹣,
故选:D.
2.解:以AB所在的直线为x轴,以线段AB的垂直平分线所在的直线为y轴建立平面直角坐标系:
∴A(﹣30,0),B(30,0),D(15,150),
设抛物线的解析式为y=a(x+30)(x﹣30),将(15,150)代入,得:
150=a(15+30)(15﹣30),
解得:a=﹣,
∴y=﹣(x+30)(x﹣30)
=﹣x2+200,
∴抛物线顶端O的坐标为(0,200),
∴此抛物线顶端O到连桥AB距离为200m.
故选:B.
3.解:∵将y=与y=﹣联立得:,解得:.
∴点B的坐标为(﹣2,1).
由抛物线的解析式可知抛物线的顶点坐标为(h,k).
∵将x=h,y=k,代入得y=﹣得:﹣h=k,解得k=﹣,
∴抛物线的解析式为y=(x﹣h)2﹣h.
如图1所示:当抛物线经过点C时.
将C(0,0)代入y=(x﹣h)2﹣h得:h2﹣h=0,解得:h1=0(舍去),h2=.
如图2所示:当抛物线经过点B时.
将B(﹣2,1)代入y=(x﹣h)2﹣h得:(﹣2﹣h)2﹣h=1,整理得:2h2+7h+6=0,解得:h1=﹣2,h2=﹣(舍去).
综上所述,h的范围是﹣2≤h≤.
故选:A.
4.解:∵y=﹣t2+12t+2
=﹣(t2﹣12t+36)+38
=﹣(t﹣6)2+38,
∴当t=6时,温度y有最大值,最大值为38℃.
∴当4≤t≤8时,该地区的最高温度是38℃.
故选:A.
5.解:由题意可设抛物线的解析式为y=a(x﹣20)2+k,
将(0,1),(20,11)分别代入,得:,解得:,
∴y=﹣(x﹣20)2+11
=﹣x2+x+1,
故A错误;
∵坡度为1:10,
∴直线OA的解析式为y=0.1x,
当x=40时,y=0.1×40=4,
令y=4,得﹣x2+x+1=4,
∴x2﹣40x+120=0,
解得x=20±2≠40,
∴B错误;
设喷射出的水流与坡面OA之间的铅直高度为h米,
则h=﹣x2+x+1﹣0.1x=﹣x2+x+1,
∴对称轴为x=﹣=18,
∴hmax=9.1,故C正确;
将喷灌架向后移动7米,则图2中x=30时抛物线上的点的纵坐标值等于x=37时的函数值,
当x=37时,y=﹣×372+37+1=3.775,
在图2中,当x=30时,点B的纵坐标为:0.1×30+2.3=5.3,
则点A的纵坐标为5.3﹣2.3=3<3.775,故D错误.
故选:C.
6.解:∵Rt△OAB的顶点A(﹣2,4)在抛物线y=ax2上,
∴4=a×(﹣2)2,
解得:a=1
∴解析式为y=x2,
∵Rt△OAB的顶点A(﹣2,4),
∴OB=OD=2,
∵Rt△OAB绕点O顺时针旋转90°,得到△OCD,
∴CD∥x轴,
∴点D和点P的纵坐标均为2,
∴令y=2,得2=x2,
解得:x=±,
∵点P在第一象限,
∴点P的坐标为:(,2)
故选:C.
7.解:∵CO=2AO,而CO=BO,AB=3,
∴AO=1,BO=OC=2,即A(﹣1,0),B(2,0),C(0,﹣2),
∴二次函数的解析式为y=x2﹣x﹣2,故A错误.
∵二次函数的对称轴为x=,
∴当x>0时,y随着x的增大而先减小再增大,故B错误.
∵此二次函数的最小值为﹣,
∴此抛物线与直线y=﹣只有一个交点,C正确.
∵要使△MAB的面积等于4,须使M到x轴的距离为,这样的点共有2个,故D错误.
故选:C.
8.解:设矩形的长为xcm,则宽为(20÷2﹣x)cm,令矩形面积为ycm2,由题意得:
y=x(20÷2﹣x)
=x(10﹣x)
=﹣x2+10x
=﹣(x﹣5)2+25,
∴当x=5时,y有最大值为25,
∴该矩形面积的最大值是25cm2.
故答案为:25.
9.解:由图象可知图形G关于直线x=1对称,故①正确;
∵半圆圆心M的坐标为(1,0).
连接CM,如图:
∵AB=4,半圆圆心M的坐标为(1,0).
∴OM=1,MC=2,
∴OC==,
∵点D的坐标为(0,﹣3),
∴OD=3,
∴CD=OD+OC=3+,故②正确;
观察图象,可知图形G围成区域内(不含边界)恰有13个整点,故③错误;
由图象可知当a=﹣4或a=2时,直线y=a与图形G有一个公共点,故④错误.
综上,正确的有①②.
故答案为:①②.
10.解:∵抛物线y=ax2经过C(4,3),
∴抛物线的解析式为y=x2,
∵C是线段AB的中点,
∴B(0,6),A(8,0),
设点D的坐标为(0,a),
则点E的坐标为(a,0),
∵点P为DE的中点,
∴点P的坐标为(a,),
∵点P在抛物线y=x2上,
∴=×(a)2,
解得:a=,
∴点P的坐标为:(,),
设点D的坐标为(a,0),
则点E的坐标为(0,a),
∵点P为DE的中点,
∴点P的坐标为(,a),
∵点P在抛物线y=x2上,
∴a=×(a)2,
解得:a=8,
∴点P的坐标为:(4,3).
故答案为:(,)或(4,3).
11.解:∵抛物线的解析式为y=﹣x+4,
∴点A的坐标为(0,4),
∵立柱MN到OA的水平距离为3m,MN左侧抛物线的最低点D与MN的水平距离为1m,
∴点N左侧的抛物线的顶点的横坐标为2,点N的坐标为(3,),
设点N左侧的抛物线的解析式为y=a(x﹣2)2+k,把(0,4),(3,)分别代入解析式,得:
,
解得,
∴该抛物线的解析式为y=(x﹣2)2+2,
∴点D到地面的距离为2m.
故答案为:2m.
12.解:如图所示,以AB所在直线为x轴,AD所在直线为y轴,建立平面直角坐标系,过点G作GQ⊥AD于点G,
∵AD=2米,DE=5米,DF=1米,
∴D(0,2),E(0,7),F(0,3),
又∵GQ⊥AD,EG=4米,∠AEG=60°,
∴GQ=2(米),
∴EQ===2(米),
∴AQ=AE﹣EQ=7﹣2=5(米),
∴G(2,5),B(2,0),C(2,2),
∵点G为抛物线的顶点,
∴设抛物线的解析式为y=a+5(a≠0),将点F(0,3)代入,得:
3=a+5,
解得a=﹣,
∴抛物线的解析式为y=﹣+5,
设直线EC的解析式为y=kx+b(k≠0),将E(0,7),C(2,2)代入,得:
,
解得,
∴直线EC的解析式为y=﹣x+7,
联立,
解得,或(舍去),
∴H(,4.5),
∴射灯H离地面的高度为4.5米.
故答案为:4.5.
13.解:根据题意,知A1、A2、A3、…An的点都在函与直线x=i(i=1、2、…、n)的图象上,
B1、B2、B3、…Bn的点都在直线与直线x=i(i=1、2、…、n)图象上,
∴A1(1,)、A2(2,2)、A3(3,)…An(n,n2);
B1(1,﹣)、B2(2,﹣1)、B3(3,﹣)…Bn(n,﹣);
∴A1B1=|﹣(﹣)|=1,
A2B2=|2﹣(﹣1)|=3,
A3B3=|﹣(﹣)|=6,
…
AnBn=|n2﹣(﹣)|=;
∴=1,
=,
…
=.
∴,
=1++…+,
=2[+++…+],
=2(1﹣+﹣+﹣+…+﹣),
=2(1﹣),
=.
故答案为:.
14.解:把x=0代入y=x+2得:y=2,
∴A(0,2).
将y=x+2与y=﹣x联立,解得:x=﹣2,y=1,
∴B(﹣2,1).
∵抛物线y=(x﹣h)2+k的顶点在直线y=﹣x上,
∴抛物线的顶点坐标为(h,k)且k=﹣h.
∴抛物线的解析式为y=(x﹣h)2﹣h.
如图1所示:
当抛物线经过点C(O)时,抛物线恰好与BC、AB均有交点,
将点C(0,0)代入y=(x﹣h)2﹣h得:h2﹣h=0,解得h=0(舍去)或h=.
如图2所示:当抛物线经过点B时,抛物线恰好与BC、AB均有交点
此时点B恰好为抛物线的顶点,
∴h=﹣2.
∴当﹣2≤h≤时,抛物线与菱形的边AB、BC都有公共点.
故答案为:﹣2≤h≤.
15.解:由图象可知,
抛物线的顶点坐标为(5,4),过点(10,0),
设抛物线的解析式为:y=a(x﹣5)2+4,
则0=a(10﹣5)2+4,
解得,a=﹣,
即这条抛物线的解析式为:y=﹣(x﹣5)2+4.
16.解:(1)=2×,
解得a=40,
经检验a是原方程的根,
∴a的值为40;
(2)①把a=40代入y=x2+x,
得y=×402+×40=86<125,
答:第a天接种完成后,B市的接种人数没有超过A市;
②由题意前40天B市接种人数少于A市,
设A市接种人数与时间的函数关系式为y=kx+b(k≠0),
将(40,125),(100,215)代入,得:,
解得:,
∴y=x+65(40≤x≤100),
∴当A,B两市接种人数恰好相同时,x+65=x2+x,
解得:x1=﹣25(舍去),x2=52,
答:第52天接种完成后,A,B两市接种人数恰好相同.
17.解:(1)设y=kx+b(k≠0),
由题意得:,
解得:,
∴y与x的函数关系式为:y=﹣10x+530;
故答案为:y=﹣10x+530;
(2)①当x=45时,m=﹣45×10+530=80,
该商场购进玩具单价为:30﹣(2300÷230)=20(元),
故答案为:80;20.
②由题意得:
w=(x﹣20)?y,
=(x﹣20)(﹣10x+530),
=﹣10x2+730x﹣10600,
=﹣10(x﹣36.5)2+2722.5,
∵﹣10<0,
∴当x=36.5时,y有最大值2722.5,
∴w与x的函数关系式为w=﹣10x2+730x﹣10600,
当销售单价x定为36.5元时,月销售利润最大,最大利润是2722.5元.
(3)由题意得:2340=(﹣10x+530)(x﹣20﹣n)=﹣10(x﹣53)(x﹣20﹣n),
函数的对称轴为:x==,
∵0<n≤7,n为整数,
∴20+n<53,且20<20+n≤27,
∴≤40,
∵﹣10<0,
∴在对称轴的右侧,w随x的增大而减小,
∵x≥40,
则函数在x=40处取得最大值,将x=40代入函数表达式得:
2340=(﹣10x+530)(x﹣20﹣n),解得:n=2.
故答案为:2.
18.解:根据题意得:
w=(﹣2x+40)(x﹣10)
=﹣2x2+60x﹣400
=﹣2(x﹣15)2+50,
∴当x=15时,w取得最大值,最大值为50.
∵1<15<19,
∴x=15符合题意.
∴当该商品的销售单价定为15元/件时,日销售利润最大,最大利润是50元.
19.解:(1)y=x(36﹣2x)
=﹣2x2+36x,
∵0<36﹣2x≤18,
∴9≤x<18.
∴y与x之间的函数关系式为y=﹣2x2+36x(9≤x<18);
(2)由题意得:﹣2x2+36x=160m2,
解得x1=8,x2=10,
∵9≤x<18,
∴x1=8不符合题意,
∴x=10;
(3)∵y=﹣2x2+36x
=﹣2(x﹣9)2+162,
∴当x=9时,y有最大值162.
∴墙长36﹣2x=36﹣18=18(m),
∴矩形ABCD空地的面积最大为162m2时,利用的墙长是18m.
20.解:(1)设该商品每天的销售量y(件)与销售单价x(元)之间的函数关系式为y=kx+b,
将点(3,100)、(40,80)代入一次函数关系式得:
,
解得:.
∴函数关系式为y=﹣2x+160;
(2)由题意得:(x﹣30)(﹣2x+160)=800,
整理得:x2﹣110x+2800=0,
解得:x1=40,x2=70.
∵单价不低于成本价,且不高于50元销售,
∴x2=70不符合题意,舍去.
∴销售单价定为40元时,每天的销售利润为800元;
(3)由题意得:
w=(x﹣30)(﹣2x+160)
=﹣2(x﹣55)2+1250,
∵﹣2<0,抛物线开口向下,
∴当x<55时,w随x的增大而增大,
∵30≤x≤50,
∴当x=50时,w有最大值,此时w=﹣2(50﹣55)2+1250=1200.
∴销售单价定为50元时,才能使销售该商品每天获得的利润w(元)最大,最大利润是1200元.
21.解:(1)当2<x≤5时,y=600;
当5<x≤10时,设y=kx+b(k≠0),把(5,600),(10,400)代入得:
,
解得,
∴y=﹣40x+800,
∴y与x之间的函数关系式为:
y=;
(2)设每天的销售利润为w元,
当2<x≤5时,
w=600(x﹣2)=600x﹣1200,
当x=5时,wmax=600×5﹣1200=1800(元);
当5<x≤10时,
w=(﹣40x+800)(x﹣2)
=﹣40(x﹣11)2+3240,
当x=10时,
wmax=﹣40×1+3240=3200(元).
综上所述,销售单价x为10元时,每天的销售利润最大,最大利润是3200元.
22.解:(1)由题意得:
w=(x﹣20)?y
=(x﹣20)(﹣10x+500)
=﹣10x2+700x﹣10000.
∵每件的利润不高于成本价的60%.
∴20≤x≤20(1+60%),
∴20≤x≤32,
∴w=﹣10x2+700x﹣10000(20≤x≤32).
(2)∵w=﹣10x2+700x﹣10000(20≤x≤32),
∴对称轴为直线x=﹣=35,
又∵a=﹣10<0,
∴抛物线开口向下,
∴当20≤x≤32时,w随x的增大而增大,
∴当x=32时,w有最大值,最大值为﹣10×322+700×32﹣10000=2160(元).
∴当销售单价定为32元时,每月可获得最大利润,每月的最大利润是2160元.
23.(1)设抛物线的解析式为y=a(x﹣1)2﹣
由于抛物线经过点B(﹣2,0),
∴a(﹣2﹣1)2﹣=0,
解得:a=,
∴二次函数的解析式为y=x2﹣x﹣4.
(2)易知:D点坐标为(0,﹣4),
可求得直线AD的函数解析式为y=﹣x﹣4,
由于BP∥AD,故可设直线BP的函数解析式为:
y=﹣x+b,
又BP经过点B,得:﹣×(﹣2)+b=0,
解得:b=﹣1,
从而BP的解析式为y=﹣x﹣1,
∴该直线与抛物线的交点P的坐标为(3,﹣),
又可求得点C(4,0),
∴PC==,
过点M作ME∥x轴交直线BP于点E,
设点M的坐标为(m,n),则点E的纵坐标为n,
∴点E的横坐标为﹣2n﹣2,
∴ME=﹣2n﹣2﹣m,
∵ME∥BC,MN∥PC,
∴∠E=∠PBC,∠MNE=∠BPC,
MN=PC=﹣(m+2n+2)
=﹣(m+m2﹣2m﹣8+2)
=﹣(m﹣)2+,
∴当m=时,MN有最大值,
(3)设点Q的坐标为(a,b),过点Q作QM∥x轴,过点B作BM∥y轴,交QM于点M,过点F作FN∥y轴交QM于点N,过点E作EK∥x轴交BM于点K,
∴△BMQ≌△QNF≌△EKB,
∴NF=KB=MQ=a+2,QN=EK=BM=b
∴点F的坐标为(a﹣b,a+b+2),
点E的坐标为(﹣2﹣b,a+2),
当点F在抛物线的对称轴上时,a﹣b=1,
∴a﹣(a2﹣a﹣4)=1,
解得:a=2﹣(舍去正值),
得点Q的坐标为(2﹣,1﹣),
当点E在抛物线的对称轴上时,﹣2﹣b=1,
∴﹣2﹣(a2﹣a﹣4)=1,
解得:a=1﹣(舍去正值),
得点Q的坐标为(1﹣,﹣3).
24.解:(1)抛物线y=x2﹣x﹣与x轴交于点A和点B,与y轴交于点C,
令x=0,则y=﹣;令y=0,则y=(x+1)(x﹣3)=0,则x=﹣1或x=3;
∴A(﹣1,0),B(3,0),C(0,﹣),
经过点C的直线l与抛物线交于另一点E(4,a),
∴a=×42﹣×4﹣,即a=,
∴E(4,),
设直线CE的解析式为:y=kx+b,
∴,解得,
∴直线CE的解析式为:y=x﹣;
(2)∵直线CE与x轴交于点F,
∴F(,0),
如图,过点P作x轴的垂线,交CE于点M,
设点P的横坐标为m,
∴P(m,m2﹣m﹣),M(m,m﹣),
∴MP=m﹣﹣(m2﹣m﹣)=﹣m2+m,
∴S△PCF=(xF﹣xC)?MP=××(﹣m2+m)=﹣(m﹣2)2+,
∴当m=2时,S△PCF的最大值为,此时P(2,﹣).
(3)在直线QH上是否存在点G,使得△DQG为等腰三角形,理由如下:
∵抛物线y=x2﹣x﹣=(x﹣1)2﹣,
∴D(1,0),Q(1,﹣),
∴DQ=,tan∠OCD=,
∴∠OCD=30°,
抛物线沿射线CD平移得到新抛物线y′,y′经过点D,如图,
则y′的顶点为点H(2,﹣),∠DQH=∠OCD=30°,
∴直线QH的解析式为y=x﹣.
①当DG1=DQ=时,如图所示,过点G1作G1I⊥DQ于点I,
此时∠G1DI=60°,
∴DI=DG1=,G1I=DI=2,
∴G1(3,);
②当QG1=QD=时,如图所示,过点G2作G2T⊥DQ于点T,过点G3作G3S⊥DQ于点S,
∴G2T=QG2=,TQ=G2T=2,
∴G2(1+,2﹣);
同理可得,G3S=,SQ=2,
∴G3(1﹣,﹣2﹣);
③当GD=GQ时,如图所示,此时点G4为DQ的中垂线与直线QH的交点,
∴G4的纵坐标为﹣,
∴G4(,﹣);
综上,点G的坐标为:(3,);(1+,2﹣);(1﹣,﹣2﹣);(,﹣).
25.解:(1)以抛物线的顶点为原点,抛物线的对称轴为y轴建立平面直角坐标系,如图所示:
设抛物线解析式为y=ax2,点D的坐标为D(5,m),则B(10,m﹣3),
由抛物线经过点D和点B,可得:,
解得:,
∴抛物线的解析式为y=﹣x2;
(2)由(1)可得CD距拱顶的距离为1m,水位以每小时0.2m的速度上升,从警戒线开始,到达拱顶的时间为=5(小时).
∴从警戒线开始,再持续5小时就能到达拱桥的拱顶.
26.解:(1)设y与x满足的函数表达式为y=kx+b(k≠0),
将(24,42),(30,24)分别代入,得:
,
解得:,
∴y与x满足的函数表达式为y=﹣3x+114.
(2)由题意得:
W=(x﹣20)?y
=(x﹣20)(﹣3x+114)
=﹣3x2+174x﹣2280
=﹣3(x﹣29)2+243.
∴当x=29时,W有最大值243.
∴销售价格定为29元/件时,才能使每天获得的利润W最大.
27.解:(1)①当2≤x<8时,设直线AB解析式为:y=kx+b,
将A(2,12)、B(8,6)代入得:
,
解得,
∴y=﹣x+14(2≤x<8);
②当x≥8时,y=6.
∴A类杨梅平均销售价格y与销售量x之间的函数关系式为:y=;
(2)设销售A类杨梅x吨,则销售B类杨梅(20﹣x)吨.
当2≤x<8时,
wA=x(﹣x+14)﹣x=﹣x2+13x;
wB=9(20﹣x)﹣[12+3(20﹣x)]=108﹣6x,
∴w=wA+wB﹣3×20
=(﹣x2+13x)+(108﹣6x)﹣60
=﹣x2+7x+48;
当x≥8时,
wA=6x﹣x=5x;
wB=9(20﹣x)﹣[12+3(20﹣x)]=108﹣6x,
∴w=wA+wB﹣3×20
=(5x)+(108﹣6x)﹣60
=﹣x+48.
∴w关于x的函数关系式为:w=;
(3)设该公司用132万元共购买了m吨杨梅,其中A类杨梅为x吨,B类杨梅为(m﹣x)吨,则购买费用为3m万元,A类杨梅加工成本为x万元,B类杨梅加工成本为[12+3(m﹣x)]万元,
∴3m+x+[12+3(m﹣x)]=132,
化简得:x=3m﹣60.
①当2≤x<8时,
wA=x(﹣x+14)﹣x=﹣x2+13x;
wB=9(m﹣x)﹣[12+3(m﹣x)]=6m﹣6x﹣12,
∴w=wA+wB﹣3×m
=(﹣x2+13x)+(6m﹣6x﹣12)﹣3m
=﹣x2+7x+3m﹣12.
将3m=x+60代入得:w=﹣x2+8x+48=﹣(x﹣4)2+64,
∴当x=4时,有最大毛利润64万元,
此时m=,m﹣x=;
②当x≥8时,wA=6x﹣x=5x;
wB=9(m﹣x)﹣[12+3(m﹣x)]=6m﹣6x﹣12,
∴w=wA+wB﹣3×m
=(5x)+(6m﹣6x﹣12)﹣3m
=﹣x+3m﹣12.
将3m=x+60代入得:w=48,
∴当x>8时,有最大毛利润48万元.
综上所述,购买杨梅共吨,其中A类杨梅4吨,B类吨,公司能够获得最大毛利润,最大毛利润为64万元.
28.解:(1)设y与x之间的函数解析式为y=ax2+bx+c,
根据题意得:,
解得:,
∴y=﹣x2+16x+34;
(2)令y=0,得:﹣x2+16x+34=0,
解得:x1=﹣2(舍),x2=34.;
∴从7:00开始,需要34分钟校门口的学生才能全部进校;
(3)设第x分钟时的排队等待人数为w人,
由题意得:w=y﹣2x
=﹣x2+14x+34,
当x=30时,w=4>0.
∴7点30分时所有学生不能全部完成进校.
29.解:(1)设AB长为x米,花圃面积为y平方米,由题意得:
y=x(80﹣2x)
=﹣2x2+80x
=﹣2(x﹣20)2+800,
∴对称轴为x=20,
由题意得:
,
解得22≤x<40.
∵﹣2<0,抛物线开口向下,
∴当x>20时,y随x的增大而减小,
∴当x=22时,y有最大值,最大值为792.
∴当AB长为22米时所围成的花圃面积最大,最大值是792平方米.
(2)由(1)知y=﹣2x2+80x
令y=350得:350=﹣2x2+80x,
解得:x1=5,x235,
∵22≤x<40,
∴x=35.
∴当花圃的面积为350平方米时,AB长为35米.
30.解:(1)设A型保鲜货车载重量为x吨,B型保鲜货车载重量为y吨,
由题意得:,
解之得:,
答:A型保鲜货车的满载重量为2吨,B型保鲜货车的满载重量为3吨.
(2)设储存m天之后,获得利润为w万元,根据题得:
w=(0.9+0.1m)(40﹣0.5m)﹣40×0.8﹣40×0.08m=36﹣0.45m+4m﹣0.05m2﹣40×0.8﹣40×0.08m=﹣0.05m2+0.35m+4=﹣0.05(m2﹣7m)+4=﹣0.05(m﹣3.5)2+4.6125,
∵a=﹣0.05<0,
∴w有最大值,
∵对称轴为m=3.5,且0≤m≤20,m为整数,
∴当m=3或4时,wmax=﹣0.05×0.25+4.6125=4.6
答:保鲜储存至第3或4天时,利润最大为4.6万元.
31.解:(1)意义是:购买不超过15本此种笔记本时售价为5元/本.
故答案为:购买不超过15本此种笔记本时售价为5元/本;
(2)①当0<x≤15时,y与x之间的函数关系式y=5,
②当15<x≤25时,设=kx+b根据题意得,
解得.
∴y与x之间的函数关系式y=﹣0.1x+6.5.
③当x>25时,y与x之间的函数关系式为:y=4.
综上,y与x之间的函数关系式为:y=;
(3)由题意得:
W=(﹣0.1x+6.5﹣3)x
=﹣0.1x2+3.5x
∵﹣0.1<0,对称轴x=17.5,且x为整数,
∴当x=17或18时,W有最大值30.6元,
∴当小明购买17或18本时,该文具批发部所获的利润最大,最大利润是30.6元.
32.解:(1)设y=kx+b(k≠0,b为常数),
将点(60,140),(70,120)代入,得,
解得,
∴y与x的函数关系式为y=﹣2x+260;
(2)由题意得:(x﹣50)(﹣2x+260)=2400,
化简得:x2﹣180x+7700=0,
解得:x1=70,x2=110,
∵50×(1+90%)=95,且110>95,
∴x2=110(舍去),
∴x=70.
∴销售单价应定为70元;
(3)设每天获得的利润为W元,由题意得:
W=(x﹣50)(﹣2x+260)
=﹣2(x﹣90)2+3200,
∵a=﹣2,抛物线开口向下,
∴W有最大值,当x=90时,W最大值=3200.
∴销售单价为90元时,每天获得的利润最大,最大利润是3200元.
33.解:(1)∵y与x满足一次函数的关系,
∴设y=kx+b(k≠0),
将x=12,y=1200;x=13,y=1100代入得:
,
解得:,
∴y与x的函数关系式为:y=﹣100x+2400;
(2)设线上和线下月利润总和为W元,
则W=400(x﹣2﹣10)+y(x﹣10)
=400x﹣4800+(﹣100x+2400)(x﹣10)
=﹣100(x﹣19)2+7300,
∴当x为19时,线上和线下月利润总和达到最大.
34.解:(1)(x﹣20)(﹣x+50)=﹣x2+70x﹣1000,
∴每天获得的利润为(﹣x2+70x﹣1000)元;
(2)设每天可获得的利润为w,由题意得:
w=﹣x2+70x﹣1000
=﹣(x2﹣70x)﹣1000
=﹣(x2﹣70x+352﹣352)﹣1000
=﹣(x﹣35)2+225,
∴当x=35时,w有最大值225.
∴当每千克售价为35元时,每天可获得最大利润;
(3)由题意得:﹣(x﹣35)2+225=200,
∴(x﹣35)2=25,
∵平方等于25的数是5或﹣5,
∴x﹣35=5,或x﹣35=﹣5,
∴x=40或x=30,
∵30<x<50,
∴x=40.
∴若每天获得利润200元,那么每千克售价应定为40元.
35.解:(1)将A、C的坐标(﹣3,0)、(0,2)代入函数式且对称轴为x=﹣2,,
∴,
∴抛物线的解析式为:y=x2+x+2.
(2)由点A、C的坐标(﹣3,0)、(0,2)可知,直线AC为:y=x+2,
∵DE∥AC,
kDE=kAC,
∴kDE=,
∵D与C关于
x=﹣2对称,
∴D(﹣4,2),
∴DE直线为:y=,
联立,,
∴,
∴E的横坐标为1,
代入可得,y=,
∴E(1,),
连接DC,
∵DE∥AC,
∴S△DEG=S△DEC,
令lDE的x=0,
∴y=,
∴M(0,),
∴S△DEC=S△DCM+S△ECM=,
∴S△DEG=,
∵S△EFG=S△DEF﹣S△DEG=S△DEF﹣,
∴△EFG的面积最大,
作FK⊥x轴,交DE于K,
∵F在抛物线上,
设F为(t,),
∴K(t,),
∴S△DEF=S△DFK+S△EFK=(xE﹣xD)(yK﹣﹣yF)=(﹣)=﹣,
∴当t=﹣时,三角形DEF面积最大,面积为:,
∴当F(﹣,﹣)时,S△EFG最大为.
(3)假设存在,
∵C(0,2),F(﹣,﹣),
∴设Q(m,m2+m+2),P(xP,yP),
∵P、Q、F、C为顶点的四边形为矩形,
∴m≠0,m,
∴kCF==,
∴直线QF:kQF==(m+),
①当P、Q、F、C的四边形以CF为对角线,
,
∴kQC?kQF=﹣1,
∴﹣=xP+m,
,
∴4m2+2m+49=0,
∵△=262﹣4×4×49=﹣105<0,
∴无解,此时不存在.
②以CQ为对角线,
∴,
∴kCF?kQF=﹣1,
∴+xP,
,
∴,
∴,
∴.
③以CP为对角线,
,
∴kCF?kQC=﹣1,
∴x,
∴,
∴,
∴,
∴P(﹣,),
∴综上,P
为(﹣,)或(﹣,).
36.解:(1)∵抛物线过点O(0,0)、A(2m,0),
∴设抛物线的解析式为y=a(x﹣0)(x﹣2m),
∵抛物线顶点为P(m,m),
∴将点P坐标代入得:a=﹣,
∴抛物线的解析式为y=﹣x(x﹣2m);
(2)∵P(m,m),对称轴直线l⊥x轴,
∴OC=CP=m,
∴△OPC是等腰直角三角形,
∴OP=OC=m,∠OPC=45°,
∵OP=MN,
∴MN=2OP=2m,
∵M、N关于点P对称,
∴MP=NP=MN=m=OP,
∴点O、M、N三点都在以点P为圆心、OP为半径的圆上,如图
∴∠MON=90°,
∵OC=CA=m,∠OCN=∠CAN=90°,CN=CN,
∴△OCN≌△CAN,
∴∠ONC=∠ANC,
∵∠ONC=∠OPC=22.5°,
∴∠ONB=2∠OPC=45°,
∴△NOB是等腰直角三角形;
②设PM=PN=d,
∵点P坐标为(m,m),
∴M的坐标为(m,m﹣d),
∴直线OM的解析式为y=,
联立抛物线解析式得:x1=0,x2=m+d,
∴点B坐标为(m+d,),
同理点N(m,m+d)可得直线AN的解析式为y=﹣,
令x=m+d代入直线AN解析式得y=,
∴点B在AN上,即点A、B、N三点共线,
由(2)得△OCN≌△CAN,
∴∠ONM=∠CAN=∠BNM.
37.解:(1)令x=0代入y=﹣3x+3,
∴y=3,
∴B(0,3),
把B(0,3)代入y=ax2﹣2ax﹣3a,
∴3=﹣3a,
∴a=﹣1,
∴二次函数解析式为:y=﹣x2+2x+3;
(2)令y=0代入y=﹣x2+2x+3,
∴0=﹣x2+2x+3,
∴x=﹣1或3,
∴抛物线与x轴的交点横坐标为﹣1和3,
∵M在抛物线上,且在第一象限内,
∴0<m<3,
令y=0代入y=﹣3x+3,
∴x=1,
∴A的坐标为(1,0),
由题意知:M的坐标为(m,﹣m2+2m+3),
S=S四边形OAMB﹣S△AOB
=S△OBM+S△OAM﹣S△AOB
=×m×3+×1×(﹣m2+2m+3)﹣×1×3
=﹣(m﹣)2+,
∴当m=时,S取得最大值.
(3)由(2)可知:M′的坐标为(,);
②过点M′作直线l1∥l′,过点B作BF⊥l1于点F,
根据题意知:d1+d2=BF,
此时只要求出BF的最大值即可,
∵∠BFM′=90°,
∴点F在以BM′为直径的圆上,
设直线AM′与该圆相交于点H,
∵点C在线段BM′上,
∴F在优弧上,
∴当F与M′重合时,
BF可取得最大值,
此时BM′⊥l1,
∵A(1,0),B(0,3),M′(,),
∴由勾股定理可求得:AB=,M′B=,M′A=,
过点M′作M′G⊥AB于点G,
设BG=x,
∴由勾股定理可得:M′B2﹣BG2=M′A2﹣AG2,
∴﹣(﹣x)2=﹣x2,
∴x=,
∵l1∥l′,
∴∠BCA=90°,
∠BAC=45°;
方法二:过B点作BD垂直于l′于D点,过M′点作M′E垂直于l′于E点,则BD=d1,ME=d2,
∵S△ABM′=×AC×(d1+d2)
当d1+d2取得最大值时,AC应该取得最小值,当AC⊥BM′时取得最小值.
根据B(0,3)和M′(,)可得BM′=,
∵S△ABM=×AC×BM′=,
∴AC=,
当AC⊥BM′时,
∴∠BAC=45°.
38.解:(1)在y=ax2+bx﹣3中,当x=0时,y=﹣3.
∴点C(0,﹣3).
∵抛物线顶点D(1,﹣4).
∴设抛物线为:y=a(x﹣1)2﹣4.
代点C(0,﹣3)得:﹣3=a﹣4.
∴a=1.
∴抛物线为:y=(x﹣1)2﹣4=x2﹣2x﹣3.
当y=0时,x2﹣2x﹣3=0.
解得x=﹣1或x=3.
∴B(3,0).
代入y=﹣x+c得:0=﹣+c.
∴c=.
(2)分两种情况:
①当AD=DN时,根据抛物线的对称性知点B与点N重合,故N(3,0).
②当NA=ND时,点N在线段AD的垂直平分线上.
∵A(﹣1,0),D(1,﹣4).
∴AD的中点F的坐标是(,),即F(0,﹣2).
设直线AD的解析式为:y=kx+b,则:
,解得k=﹣2,b=﹣2.
∴直线AD:y=﹣2x﹣2.
设直线AD的垂直平分线为FN的表达式为:y=x+b.
代入F(0,﹣2)得:b=﹣2.
∴直线NF:y=x﹣2.
由得:或.
∵点N在y轴右侧的抛物线上.
∴N(,).
综上可知,点N的坐标为(3,0)或(,).
(3)点F的横坐标是.
如图:
在BE上选一点F,在OB上选一点M,使得FM=MB,则∠FMG=2∠ABE.
在OB上点M的左侧取一点G,使得FG=FM,则∠EFG=∠FGM+∠ABE=3∠ABE.
移动点F,当GH=2FG时,点F即为所求.
过点F作FP⊥x轴于点P,过点H作HQ⊥x轴于点Q,则GP=PM
设F(m,﹣m+),则OP=m,FP=﹣m+.
∴HQ=2FP=﹣m+3.
易得PB=2FP.∴FM=BM=PB﹣PM=2FP﹣PM.
由勾股定理得:FP2+PM2=FM2,即FP2+PM2=(2FP﹣PM)2.
∴PM=﹣m+=GP.
OG=OP﹣GP=m﹣.
GQ=2GP=﹣m+.
∴OQ=GQ﹣OG=﹣m+.
∴H(m﹣,m﹣3).
易求直线AD的表达式为:y=﹣2x﹣2,
将H代入得:m﹣3=﹣2(m﹣)﹣2.
解得:m=.
故点F的横坐标为:.
39.解:(1)∵抛物线C:y=(x﹣2)2向下平移6个单位长度得到抛物线C1,
∴C1:y=(x﹣2)2﹣6,
∵抛物线C1向左平移2个单位长度得到抛物线C2,
∴C2:y=(x﹣2+2)2﹣6,
即y=x2﹣6,
(2)过点A作AC⊥x轴于点C,过点B作BD⊥AC于点D,如图所示:
设A点坐标为(a,(a﹣2)2﹣6),
∴C点坐标为(a,0),
∵C1的对称轴x=2,
∴OC=BD=a﹣2,AC=|(a﹣2)2﹣6|,
∵∠BAO=∠ACO=90°,
∠BAD+∠OAC=∠OAC+∠AOC=90°,
∴∠BAD=∠AOC,
∵AB=OA,∠ADB=∠OCA,
∴△ABD≌△OAC(AAS),
∴BD=AC,
∴a﹣2=|(a﹣2)2﹣6|,
解得,a=4,或a=﹣1,或a=0,或a=5,
∵A点在第一象限,
∴a=4或a=5,
∴A(4,﹣2)(舍弃)或(5,3),
∴A(5,3).
(3)把y=kx代入y=x2﹣6中得,x2﹣kx﹣6=0,
∴xE+xF==k,
∴M(),
将y=x代入y=x2﹣6,中得x2+x﹣6=0,
∴xG+xH=,
∴N(),
设MN的解析式为y=mx+n(m≠0),则
,
解得,,
∴直线MN的解析式为:y=x+2,
当x=0时,y=2,
∴直线MN:y=x+2经过定点(0,2),
即直线MN经过一个定点.
40.解:(1)将A(4,0),B(,)代入y=ax2+bx,
解方程组得a=﹣1,b=4,
∴抛物线的解析式为y=﹣x2+4x,
顶点G的坐标为:(2,4).
(2)设C(c,0),则E(c,﹣c2+4c),
∵点P是第三象限内抛物线上一点,
故可设P(t,﹣t2+4t),其中t<0,
设PE:y=kx+m,则,
解得:,
∴PE:y=(4﹣t﹣c)x+ct,
令x=0,得y=ct,即M(0,ct),
∴OC=c,OM=﹣ct,
∴MC∥ND.
(3)解方程组,
得:,,
∴Q(4﹣k,4k﹣k2),
根据O,G,Q坐标可求
OG=,
OQ=,
GQ=,
∵∠OQG=90°,
∴OQ2+GQ2=OG2,
即
(4﹣k)2+(4k﹣k2)2+(2﹣k)2+(4k﹣k2﹣4)2=20,
∴(k﹣4)2+k2(k﹣4)2+(k﹣2)2+(k﹣2)4=20,
令k﹣2=t,则(t﹣2)2+(t+2)2(t﹣2)2+t2+t4=20,
展开化简得t4﹣3t2﹣2t=0,
进行因式分解得t(t+1)2(t﹣2)=0,
∴t=0或者t=﹣1或t=2,
∴k=2或者k=1或k=4,
当k=2时,Q(2,4)与G重合,不符题意,舍去,
当k=1时,Q(3,3),符合题意,
当k=4时,Q(0,0)与原点重合,不符题意,舍去,
∴k=1.
41.解:(1)由y=0,得x2﹣4x+3=0,
解得,x1=1,x2=3,
∵点A在点B的左侧,
∴点A的坐标为(1,0),点B的坐标为(3,0),
由x=0,得y=3,
∴点C的坐标为(0,3).
(2)∵y=x2﹣4x+3=(x﹣2)2﹣1,
∴点D的坐标为(2,﹣1),抛物线的对称轴为直线x=2,
设M(2,m),m<﹣1,
由DM=﹣1﹣m,
∴OM2=m2+4,BM2=m2+1,
若BM=OM,则m2+4=m2+1,此方程无解,
若BM=OB,则9=m2+1,
解得m=﹣2或m=2(不合题意,舍去),
∴t=DM=2﹣1,
若OM=OB,则9=m2+4,
解得m=﹣或m=(不合题意,舍去),
∴t=DM=﹣1,
综上所述,当t=2﹣1或﹣1时,△OMB为等腰三角形;
(3)存在点P,使∠PBF被BA平分,
在y轴上取一点N(0,﹣),连接BN交抛物线于点P,则∠PBO=∠EBO,
设直线BN的解析式为y=kx﹣,
∴3k﹣=0,
解得,k=,
∴直线BN的解析式为:y=x﹣,
解方程:x2﹣4x+3=x﹣,
解得,x1=,x2=3(不合题意,舍去),
当x=时,y=﹣,
∴P(,﹣),
∴存在点P(,﹣),使得∠PBF被BA平分.
42.解:(1)由题意可得,,
解得,,
∴抛物线的解析式为:y=x2﹣2x﹣3;
(2)由(1)知,D(1,﹣4),C(0,﹣3),
∴E(1,4),
∵直线y=mx+1过点A(﹣1,0),
∴直线AF:y=x+1,
如图1,分别过点B,E作BG∥y轴,EH∥y轴,与AF交于点G,H,
∴S1=(xP﹣xA)?EH,S2=(xP﹣xA)?BG
∴=,
∵B(3,0),
∴G(3,4),BG=4,
∵E(1,4),
∴H(1,2),EH=2,
∴===,
∴的值是一个定值,这个定值为;
(3)如图2,过点B作BP⊥AC于点P,作∠BTC=∠BMC,过点O作ON∥BT交AC于点N,
∴∠ONC=∠BTC=∠BMC,
∴BT=BM,点P是点T,点M的中点,
∵A(﹣1,0),C(0,﹣3),
∴直线AC:y=﹣3x﹣3,
∵BP⊥AC,B(3,0),
∴直线BP:y=x﹣1,
联立,解得,
∴P(﹣,﹣),
∵B(3,0),D(1,﹣4),
∴直线BD:y=2x﹣6,
联立,解得,
∴M(,﹣),
∴由中点坐标公式可得,T(﹣,),
设直线BT的解析式为y=kx+b,
∴,解得,,
∴y=﹣x+,
∴直线ON的表达式为:y=﹣x,
联立,解得,
∴N(﹣,).
43.解:(1)∵AB∥OD,AB的解析式为y=x+2,
∴OD的解析式为y=x;C点的坐标为(0,2);
又∵DC⊥y轴;
∴D点的纵坐标为2,将y=2代入y=x中,得x=2,
∴D点的坐标为(2,2)
将点D(2,2)代入y=ax2(a>0)中,解得a=;
(2)由(1)知,抛物线的解析式为y=x2,
∴
解得,;
∴;;
∴由图可知点A坐标为,
点B的坐标为,
由图可知,直线AH过原点,
∴设AH的解析式为y=kx,将A点坐标代入,
解得k=;
∴,
又∵BG⊥x轴交x轴于点G,BG的延长线交AO的延长线于点H,
∴点G的坐标为()点H的横坐标为,
将点H横坐标代到y=x中得y=﹣2,
∴点H的坐标为();
∴BH=BG+GH=;
设AG所在直线的解析式为y1=k1x+b,代入A、G两点的坐标得:
解得:k1=,b=;
∴y1=x+;
∴OK=;
∴OK?BH==4.
(3)∵a=1,
∴设平移后抛物线的解析式为y=x2+bx+c,
将A(﹣1,0),B(2,0)两点代入可得b=﹣1,c=﹣2;
∴y=x2﹣x﹣2;
设点P的坐标为(0,e)
∴将点A、P坐标代入可得AM所在直线的解析式为yAM=ex+e;
将点B、P坐标代入可得BN所在直线的解析式为yBN=﹣x+e;
又∵N、M在抛物线上,
∴
解得xM=e+2,∴
解得,∴;
∵AB=3,
∴S3=S△APB=?AB?OP=;
S1=S△PNA=S△NAB﹣S△APB
=
=;
S2=S△PMB=S△MAB﹣S△APB
=
=
代入得
e2=13(e>0)
∴e=,
∴P(0,).
同课章节目录
