正方形
图片预览


文档简介
(共27张PPT)
19.2.3 正方形(2)
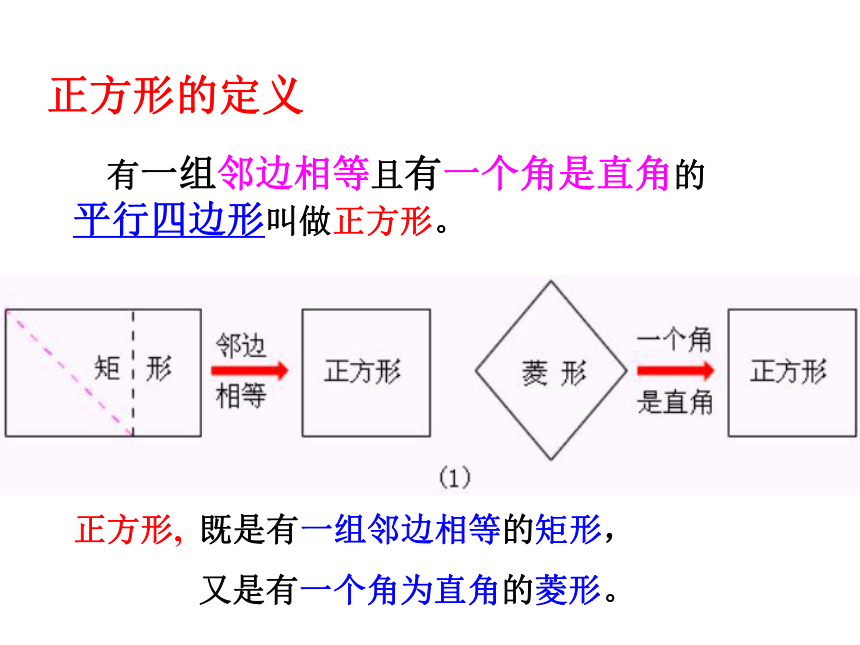
正方形的定义
正方形, 既是有一组邻边相等的矩形,
又是有一个角为直角的菱形。
有一组邻边相等且有一个角是直角的 平行四边形叫做正方形。
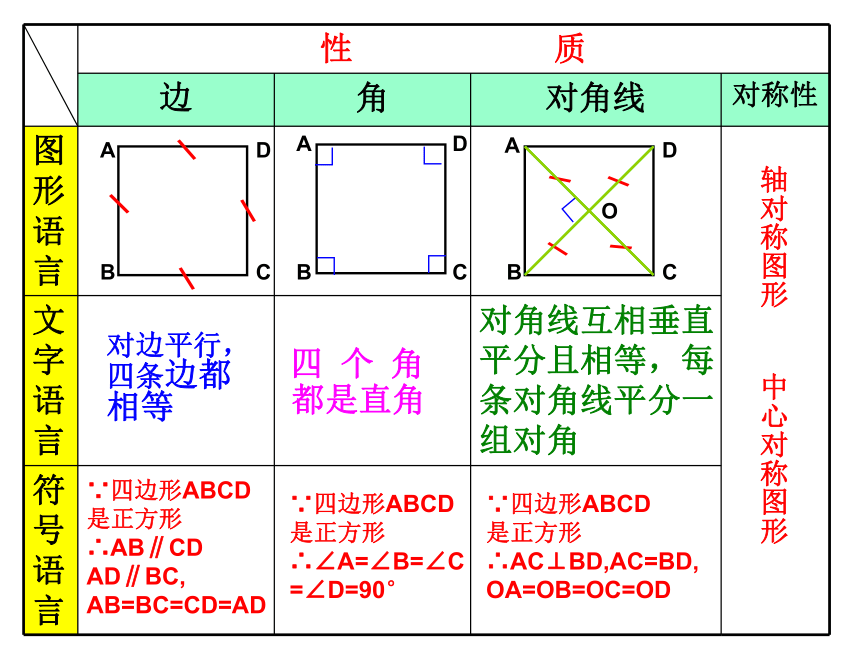
性 质
边 角 对角线 对称性
图形语言
文字语言
符号语言
A
C
D
\
B
A
C
D
B
A
C
D
B
\
\
\
∟
∟
∟
∟
O
\
\
\
\
∟
对边平行, 四条边都相等
四 个 角
都是直角
对角线互相垂直平分且相等,每条对角线平分一组对角
∵四边形ABCD是正方形
∴AB∥CD AD∥BC, AB=BC=CD=AD
∵四边形ABCD是正方形
∴∠A=∠B=∠C=∠D=90°
∵四边形ABCD
是正方形
∴AC⊥BD,AC=BD,OA=OB=OC=OD
轴对称图形 中心对称图形
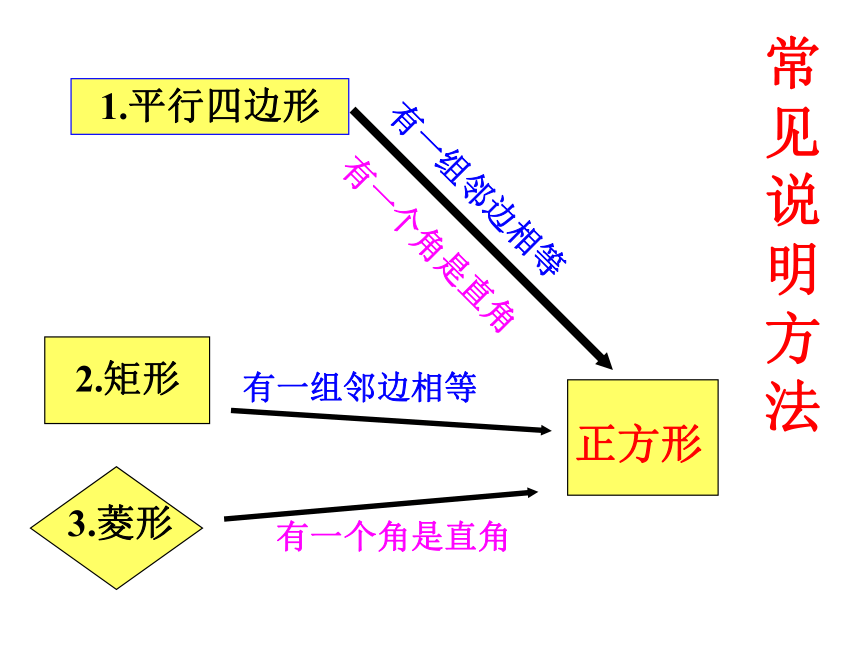
正方形
2.矩形
有一组邻边相等
3.菱形
有一个角是直角
1.平行四边形
有一组邻边相等
有一个角是直角
常
见
说
明
方
法
例1:
1、要使一个菱形成为正方形需增加的条件
是 . (填上一个条件即可)
2、要使一个矩形成为正方形需添加的条件
是 .(填上一个条件即可)
3、下列正确的是( )
A.四边相等的四边形是正方形
B.四角相等的四边形是正方形
C.对角线垂直的平行四边形是正方形
D.对角线互相垂直平分且相等的四边形
是正方形
有一组邻边相等
有一个角是直角
D
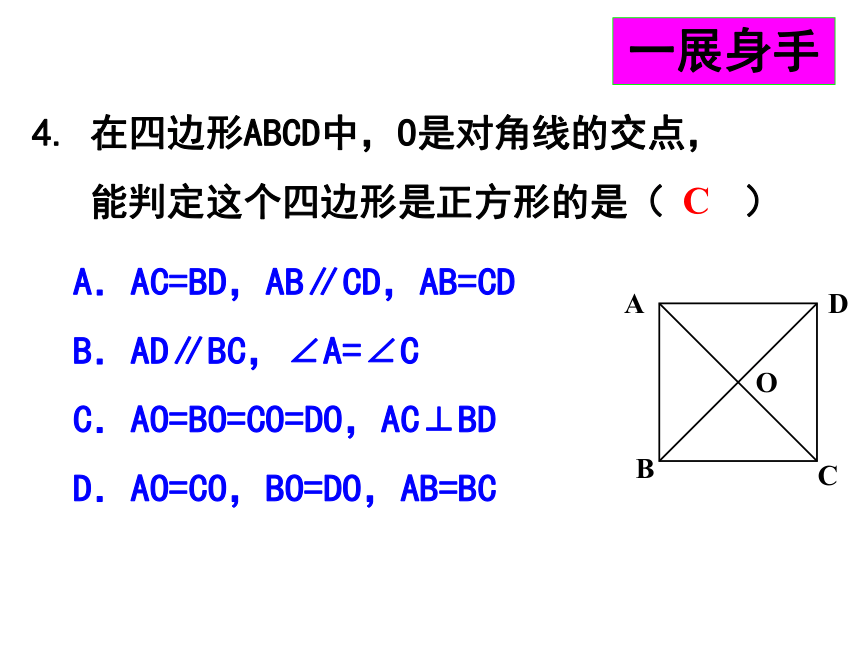
一展身手
4. 在四边形ABCD中,O是对角线的交点,
能判定这个四边形是正方形的是( )
A.AC=BD,AB∥CD,AB=CD
B.AD∥BC,∠A=∠C
C.AO=BO=CO=DO,AC⊥BD
D.AO=CO,BO=DO,AB=BC
A
B
C
D
O
C
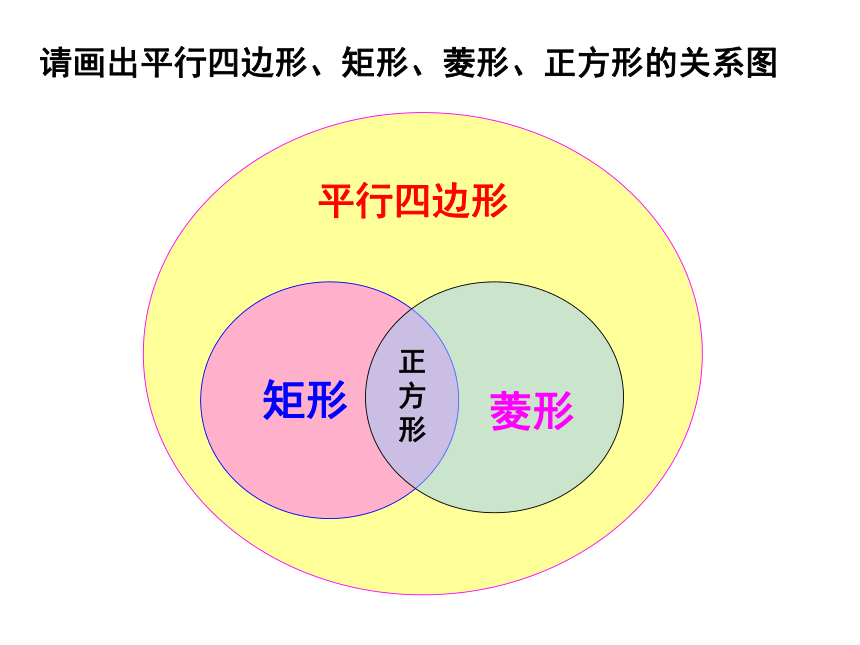
平行四边形
矩形
菱形
正
方
形
请画出平行四边形、矩形、菱形、正方形的关系图
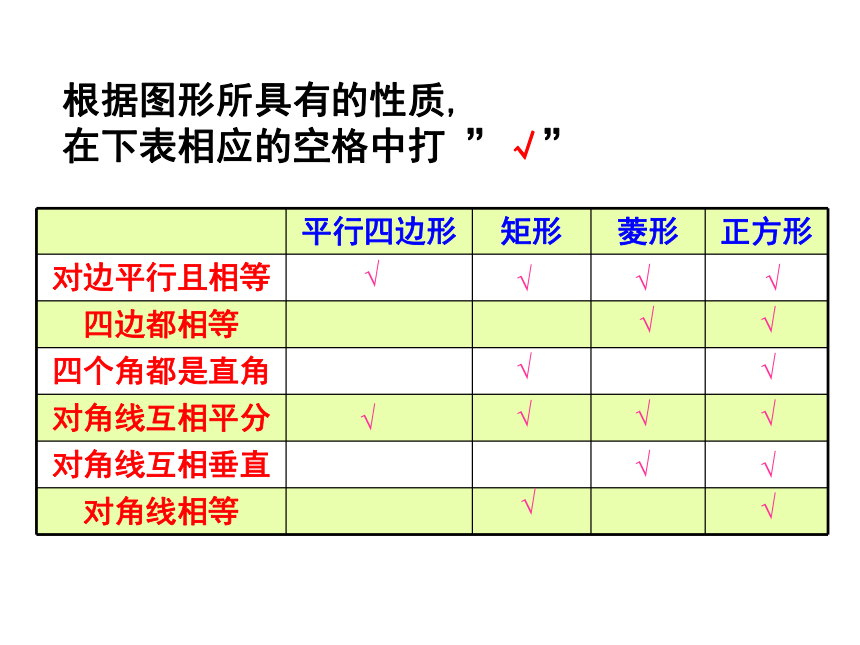
根据图形所具有的性质,
在下表相应的空格中打 ”√”
平行四边形 矩形 菱形 正方形
对边平行且相等
四边都相等
四个角都是直角
对角线互相平分
对角线互相垂直
对角线相等
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
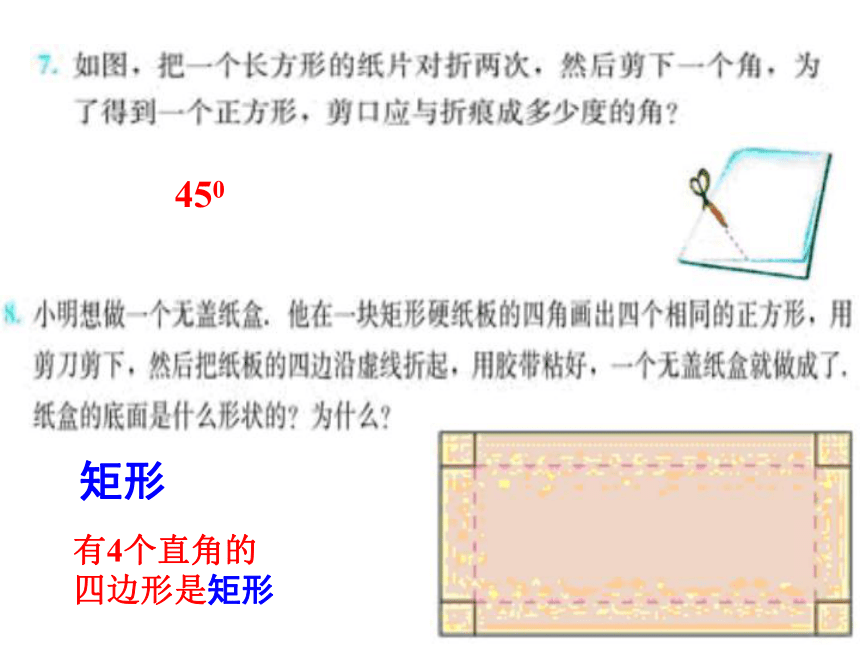
450
矩形
有4个直角的四边形是矩形
1
∠BCD=22.50
∠A=∠BCD=22.50
AE=CE
∠1 =∠BCD=22.50
∠DCE=450
A
B
C
D
O
E
F
分析:要证明BM=CN,
可以考虑证哪两个三角形全等
你能完成证明吗
AB=BC,∠1=∠2=45 ° 条件够吗?
还需要的条件是 AM=BN
△ABM≌△BCN
你所要证明的两个三角形已经满足了哪些条件
由正方形可以得到的条件有:
例2.如图(3),正方形ABCD中,AC、BD相交于O,
MN∥AB且MN分别交OA、OB于M、N,
求证:BM=CN。
例2.如图(3),正方形ABCD中,AC、BD相交于O,
MN∥AB且MN分别交OA、OB于M、N,
求证:BM=CN。
证明:
∵四边形ABCD是正方形 ∴OA=OB ,
∠1=∠2=∠3=45° 又∵MN∥AB
∴∠OMN=∠1=∠3
=∠ONM=45° ∴OM=ON ∴OA-OM=OB-ON 即AM=BN
下面大家自己完成证明
例3.已知:如图(4)在正方形ABCD中,F为CD延长线
上一点,CE⊥AF于E,交AD于M,
求证:∠MFD=45°
分析:
欲证∠MFD=45°,
由于△MDF是直角三角形,
只须证△MDF是等腰三角形,
即只要证 _____=_____
要证MD=FD,大家只须证得哪两个三角形全等
试一试,看能不能完成证明
△CMD≌△ADF
证明:
∵CE⊥AF ∴∠ADC=∠AEM=90° 又∵∠CMD=∠AME ∴∠1=∠2 又∵CD=AD,
∠ADF=∠MDC ∴Rt△CDM≌Rt△ADF(AAS) ∴DM=DF
下面的证明请大家完成
例3.已知:如图(4)在正方形ABCD中,F为CD延长线
上一点,CE⊥AF于E,交AD于M,
求证:∠MFD=45°
例4.如图(6),△ABC的外面作
正方形ABDE和ACFG,
连结BG、CE,交点为N。 求证:∠CEA=∠ABG
分析:欲证∠CEA=∠ABG,
想一想证明两个角相等的方法,
证明:∵四边形ABDE和四边形ACFG是正方形 ∴AE=AB AG=AC ∠1=∠2=90° 又∵∠EAC=∠1+∠BAC=90°+∠BAC ∠BAG=∠2+∠BAC=90°+∠BAC ∴∠EAC=∠BAG ∴△AEC≌△ABG (SAS)
∴∠CEA=∠ABG
练习1.
已知:正方形ABCD对角线AC、BD相交于点O,
且AB=acm,如图(2)。
求:AC的长及正方形的面积S。
练习2.
已知:在正方形ABCD中,对角线AC、
BD相交于点O,且AC=6 cm,如图
求:正方形的面积S。
练习3.
如图(5),在AB上取一点C,以AC、BC为正方形的一边在同一侧作正方形AEDC和BCFG连结AF、BD延长BD交AF于H。 求证:(1) △ACF≌△DCB; (2) BH⊥AF
证明:
例题赏析
⒉在正方形ABCD中,AC是对角线,AE平分∠BAC,试猜想AB、AC、BE之间的关系,并证明你的猜想.
G
F
E
D
A
B
C
例题赏析
⒊在正方形ABCD中,对角线AC、BD相交于点O,点Q是CD上任意一点,DP⊥AQ交BC于点P.
⑴求证:DQ=CP;
⑵OP与OQ有何关系?试证明你的结论.
如图,以△ABC的边AB、AC向形外作正方形ABDE和ACFG,M是BC的中点.
求证:
⑴CE=BG;
⑵EG=2AM.
H
M
E
D
F
G
B
C
A
求证:矩形的四个角的平分线所围成的四边形是正方形.
练习:在△ABC中,AB=AC,D是BC的中点,DE⊥AB,
DF⊥AC,垂足分别是E,F.
1)试说明:DE=DF
2)只添加一个条件,使四边形EDFA是正方形.
请你至少写出两种不同的添加方法.(不另外
添加辅助线,无需证明)
1.一个矩形的2条对角线互相垂直,它是正方形吗?
2.一个菱形的2条对角线相等,它是正方形吗?
思考:
小结
1、正方形定义
有一组邻边相等并且有一个角是直角的平行四边形是正方形
2、正方形有那些性质
对边平行,四条边都相等
四个角都是直角
对角线互相垂直平分且相等,
每条对角线平分一组对角
边:
角:
对角线:
小结
19.2.3 正方形(2)
正方形的定义
正方形, 既是有一组邻边相等的矩形,
又是有一个角为直角的菱形。
有一组邻边相等且有一个角是直角的 平行四边形叫做正方形。
性 质
边 角 对角线 对称性
图形语言
文字语言
符号语言
A
C
D
\
B
A
C
D
B
A
C
D
B
\
\
\
∟
∟
∟
∟
O
\
\
\
\
∟
对边平行, 四条边都相等
四 个 角
都是直角
对角线互相垂直平分且相等,每条对角线平分一组对角
∵四边形ABCD是正方形
∴AB∥CD AD∥BC, AB=BC=CD=AD
∵四边形ABCD是正方形
∴∠A=∠B=∠C=∠D=90°
∵四边形ABCD
是正方形
∴AC⊥BD,AC=BD,OA=OB=OC=OD
轴对称图形 中心对称图形
正方形
2.矩形
有一组邻边相等
3.菱形
有一个角是直角
1.平行四边形
有一组邻边相等
有一个角是直角
常
见
说
明
方
法
例1:
1、要使一个菱形成为正方形需增加的条件
是 . (填上一个条件即可)
2、要使一个矩形成为正方形需添加的条件
是 .(填上一个条件即可)
3、下列正确的是( )
A.四边相等的四边形是正方形
B.四角相等的四边形是正方形
C.对角线垂直的平行四边形是正方形
D.对角线互相垂直平分且相等的四边形
是正方形
有一组邻边相等
有一个角是直角
D
一展身手
4. 在四边形ABCD中,O是对角线的交点,
能判定这个四边形是正方形的是( )
A.AC=BD,AB∥CD,AB=CD
B.AD∥BC,∠A=∠C
C.AO=BO=CO=DO,AC⊥BD
D.AO=CO,BO=DO,AB=BC
A
B
C
D
O
C
平行四边形
矩形
菱形
正
方
形
请画出平行四边形、矩形、菱形、正方形的关系图
根据图形所具有的性质,
在下表相应的空格中打 ”√”
平行四边形 矩形 菱形 正方形
对边平行且相等
四边都相等
四个角都是直角
对角线互相平分
对角线互相垂直
对角线相等
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
450
矩形
有4个直角的四边形是矩形
1
∠BCD=22.50
∠A=∠BCD=22.50
AE=CE
∠1 =∠BCD=22.50
∠DCE=450
A
B
C
D
O
E
F
分析:要证明BM=CN,
可以考虑证哪两个三角形全等
你能完成证明吗
AB=BC,∠1=∠2=45 ° 条件够吗?
还需要的条件是 AM=BN
△ABM≌△BCN
你所要证明的两个三角形已经满足了哪些条件
由正方形可以得到的条件有:
例2.如图(3),正方形ABCD中,AC、BD相交于O,
MN∥AB且MN分别交OA、OB于M、N,
求证:BM=CN。
例2.如图(3),正方形ABCD中,AC、BD相交于O,
MN∥AB且MN分别交OA、OB于M、N,
求证:BM=CN。
证明:
∵四边形ABCD是正方形 ∴OA=OB ,
∠1=∠2=∠3=45° 又∵MN∥AB
∴∠OMN=∠1=∠3
=∠ONM=45° ∴OM=ON ∴OA-OM=OB-ON 即AM=BN
下面大家自己完成证明
例3.已知:如图(4)在正方形ABCD中,F为CD延长线
上一点,CE⊥AF于E,交AD于M,
求证:∠MFD=45°
分析:
欲证∠MFD=45°,
由于△MDF是直角三角形,
只须证△MDF是等腰三角形,
即只要证 _____=_____
要证MD=FD,大家只须证得哪两个三角形全等
试一试,看能不能完成证明
△CMD≌△ADF
证明:
∵CE⊥AF ∴∠ADC=∠AEM=90° 又∵∠CMD=∠AME ∴∠1=∠2 又∵CD=AD,
∠ADF=∠MDC ∴Rt△CDM≌Rt△ADF(AAS) ∴DM=DF
下面的证明请大家完成
例3.已知:如图(4)在正方形ABCD中,F为CD延长线
上一点,CE⊥AF于E,交AD于M,
求证:∠MFD=45°
例4.如图(6),△ABC的外面作
正方形ABDE和ACFG,
连结BG、CE,交点为N。 求证:∠CEA=∠ABG
分析:欲证∠CEA=∠ABG,
想一想证明两个角相等的方法,
证明:∵四边形ABDE和四边形ACFG是正方形 ∴AE=AB AG=AC ∠1=∠2=90° 又∵∠EAC=∠1+∠BAC=90°+∠BAC ∠BAG=∠2+∠BAC=90°+∠BAC ∴∠EAC=∠BAG ∴△AEC≌△ABG (SAS)
∴∠CEA=∠ABG
练习1.
已知:正方形ABCD对角线AC、BD相交于点O,
且AB=acm,如图(2)。
求:AC的长及正方形的面积S。
练习2.
已知:在正方形ABCD中,对角线AC、
BD相交于点O,且AC=6 cm,如图
求:正方形的面积S。
练习3.
如图(5),在AB上取一点C,以AC、BC为正方形的一边在同一侧作正方形AEDC和BCFG连结AF、BD延长BD交AF于H。 求证:(1) △ACF≌△DCB; (2) BH⊥AF
证明:
例题赏析
⒉在正方形ABCD中,AC是对角线,AE平分∠BAC,试猜想AB、AC、BE之间的关系,并证明你的猜想.
G
F
E
D
A
B
C
例题赏析
⒊在正方形ABCD中,对角线AC、BD相交于点O,点Q是CD上任意一点,DP⊥AQ交BC于点P.
⑴求证:DQ=CP;
⑵OP与OQ有何关系?试证明你的结论.
如图,以△ABC的边AB、AC向形外作正方形ABDE和ACFG,M是BC的中点.
求证:
⑴CE=BG;
⑵EG=2AM.
H
M
E
D
F
G
B
C
A
求证:矩形的四个角的平分线所围成的四边形是正方形.
练习:在△ABC中,AB=AC,D是BC的中点,DE⊥AB,
DF⊥AC,垂足分别是E,F.
1)试说明:DE=DF
2)只添加一个条件,使四边形EDFA是正方形.
请你至少写出两种不同的添加方法.(不另外
添加辅助线,无需证明)
1.一个矩形的2条对角线互相垂直,它是正方形吗?
2.一个菱形的2条对角线相等,它是正方形吗?
思考:
小结
1、正方形定义
有一组邻边相等并且有一个角是直角的平行四边形是正方形
2、正方形有那些性质
对边平行,四条边都相等
四个角都是直角
对角线互相垂直平分且相等,
每条对角线平分一组对角
边:
角:
对角线:
小结
