2021-2022学年苏科版八年级数学上册第1章全等三角形 能力达标专题突破训练(word解析版)
文档属性
| 名称 | 2021-2022学年苏科版八年级数学上册第1章全等三角形 能力达标专题突破训练(word解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 300.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-23 10:30:48 | ||
图片预览


文档简介
2021-2022学年苏科版八年级数学上册《第1章全等三角形》能力达标
专题突破训练(附答案)
一.选择题(共10小题,满分30分,每小题3分)
1.如图,若△ABC≌△ADE,则下列结论中一定成立的是( )
A.∠ABC=∠AED
B.∠BAD=∠CAE
C.AB=AE
D.AC=DE
2.如图,已知点M,N分别在AC,AB上,∠MBN=∠MCN,现添加下面的哪一个条件后,仍不能判定△ABM≌△ACN的是( )
A.AM=AN
B.AB=AC
C.BM=CN
D.∠AMB=∠ANC
3.如图,在△ABC中,AD平分∠BAC,且AE=AF,则可直接用“SAS”判断的是( )
A.△ABD≌△ACD
B.△BDE≌△CDF
C.△ADE≌△ADF
D.△ABD≌△ABC
4.如图,点B的坐标为(4,4),作BA⊥x轴,BC⊥y轴,垂足分别为A、C,点D为线段OA的中点,点P从点A出发,在线段AB、BC上沿A→B→C运动,当OP=CD时,点P的坐标为( )
A.(4,1)
B.(4,2)
C.(2,2)
D.(4,2)或(2,4)
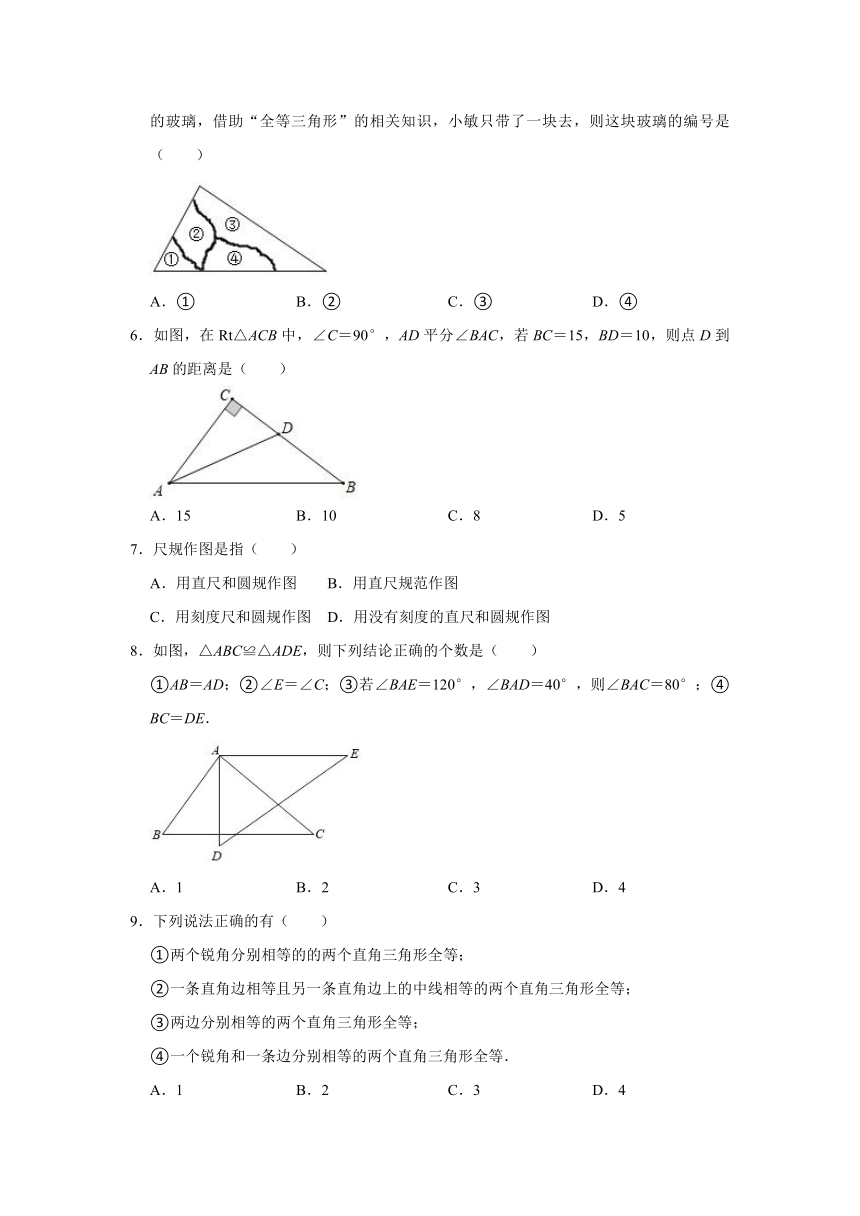
5.一块三角形玻璃,被摔成如图所示的四块,小敏想去店里买一块形状、大小与原来一样的玻璃,借助“全等三角形”的相关知识,小敏只带了一块去,则这块玻璃的编号是( )
A.①
B.②
C.③
D.④
6.如图,在Rt△ACB中,∠C=90°,AD平分∠BAC,若BC=15,BD=10,则点D到AB的距离是( )
A.15
B.10
C.8
D.5
7.尺规作图是指( )
A.用直尺和圆规作图
B.用直尺规范作图
C.用刻度尺和圆规作图
D.用没有刻度的直尺和圆规作图
8.如图,△ABC≌△ADE,则下列结论正确的个数是( )
①AB=AD;②∠E=∠C;③若∠BAE=120°,∠BAD=40°,则∠BAC=80°;④BC=DE.
A.1
B.2
C.3
D.4
9.下列说法正确的有( )
①两个锐角分别相等的的两个直角三角形全等;
②一条直角边相等且另一条直角边上的中线相等的两个直角三角形全等;
③两边分别相等的两个直角三角形全等;
④一个锐角和一条边分别相等的两个直角三角形全等.
A.1
B.2
C.3
D.4
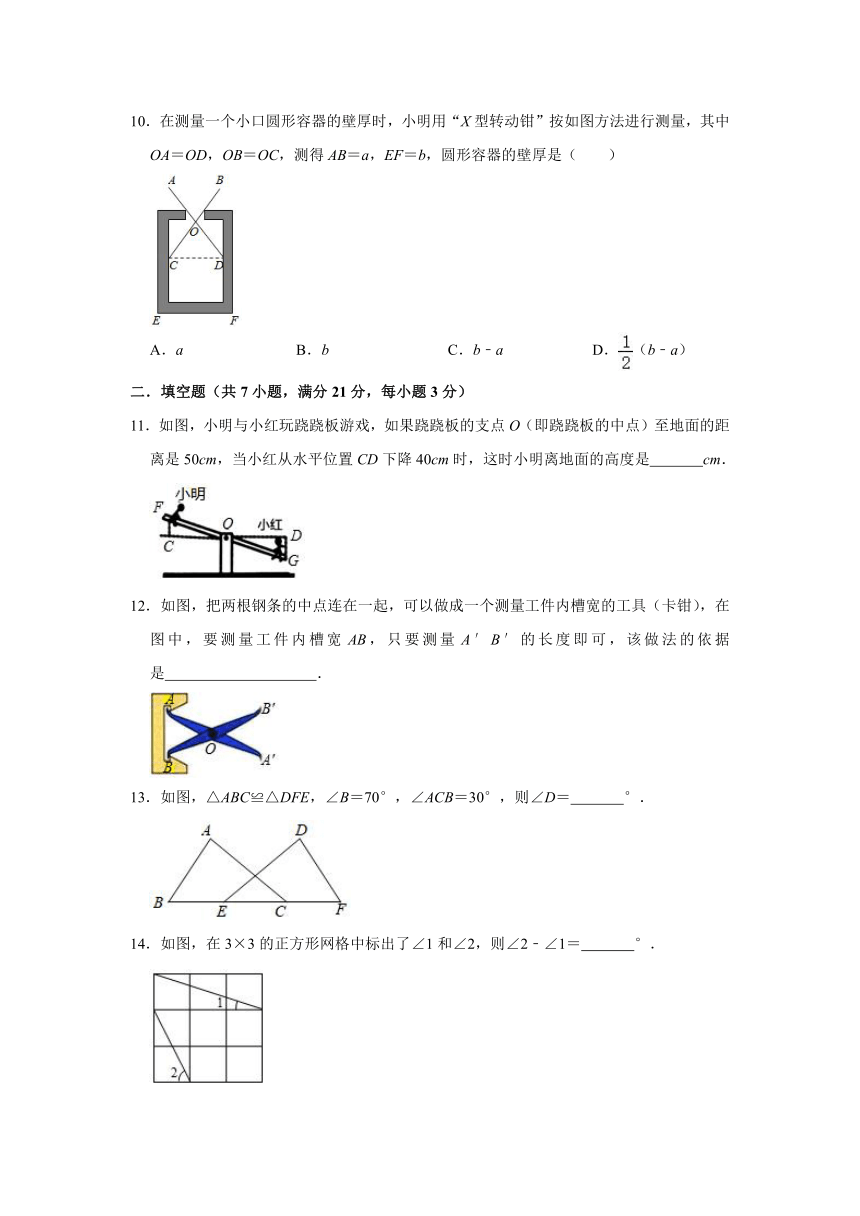
10.在测量一个小口圆形容器的壁厚时,小明用“X型转动钳”按如图方法进行测量,其中OA=OD,OB=OC,测得AB=a,EF=b,圆形容器的壁厚是( )
A.a
B.b
C.b﹣a
D.(b﹣a)
二.填空题(共7小题,满分21分,每小题3分)
11.如图,小明与小红玩跷跷板游戏,如果跷跷板的支点O(即跷跷板的中点)至地面的距离是50cm,当小红从水平位置CD下降40cm时,这时小明离地面的高度是
cm.
12.如图,把两根钢条的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳),在图中,要测量工件内槽宽AB,只要测量A′B′的长度即可,该做法的依据是
.
13.如图,△ABC≌△DFE,∠B=70°,∠ACB=30°,则∠D=
°.
14.如图,在3×3的正方形网格中标出了∠1和∠2,则∠2﹣∠1=
°.
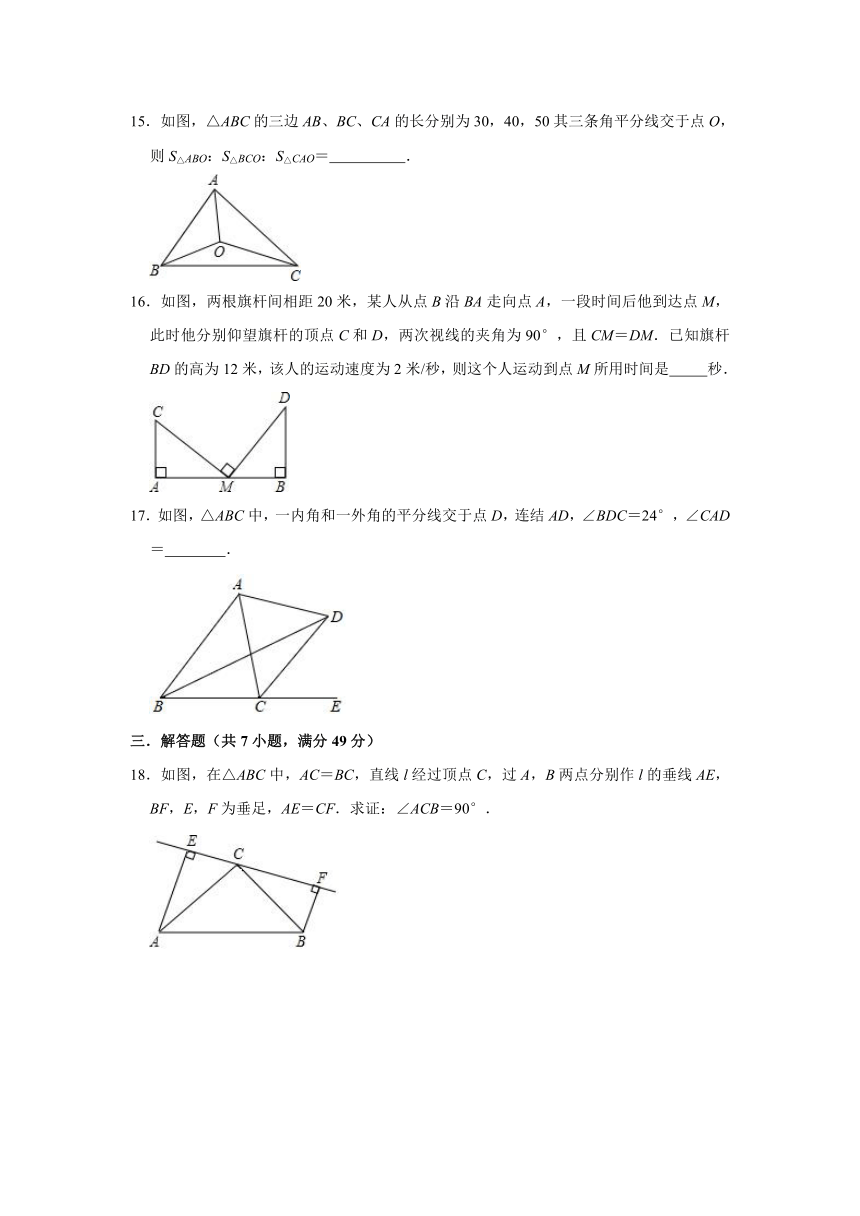
15.如图,△ABC的三边AB、BC、CA的长分别为30,40,50其三条角平分线交于点O,则S△ABO:S△BCO:S△CAO=
.
16.如图,两根旗杆间相距20米,某人从点B沿BA走向点A,一段时间后他到达点M,此时他分别仰望旗杆的顶点C和D,两次视线的夹角为90°,且CM=DM.已知旗杆BD的高为12米,该人的运动速度为2米/秒,则这个人运动到点M所用时间是
秒.
17.如图,△ABC中,一内角和一外角的平分线交于点D,连结AD,∠BDC=24°,∠CAD=
.
三.解答题(共7小题,满分49分)
18.如图,在△ABC中,AC=BC,直线l经过顶点C,过A,B两点分别作l的垂线AE,BF,E,F为垂足,AE=CF.求证:∠ACB=90°.
19.完成下列推理过程.
如图所示,点E在△ABC外部,点D在BC边上,DE交AC于F,若∠1=∠3,∠E=∠C,AE=AC,求证:△ABC≌△ADE.
证明:∵∠E=∠C(已知),
∠AFE=∠DFC
(
),
∴∠2=∠3
(
).
∵∠1=∠2(等量代换),
∴∠1+∠DAC=∠2+∠DAC
(
).
即∠BAC=∠DAE.
在△ABC和△ADE中,
∵,
∴△ABC≌△ADE
(
).
20.如图,∠A=∠B=90°,E是AB上的一点,且AE=BC,∠1=∠2.
(1)求证:Rt△ADE≌Rt△BEC;
(2)△CDE是不是直角三角形?并说明理由.
21.王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合.
(1)求证:△ADC≌△CEB;
(2)求两堵木墙之间的距离.
22.按逻辑填写步骤和理由,将下面的证明过程补充完整.
如图,四边形ABCD中,E点在AD上,∠BAE=∠BCE=∠ACD=90°,BC=EC.
(1)求证:△ABC≌△DEC.
证明:
∵∠BAE=∠BCE=∠ACD=90°(已知)
∴∠2+∠D=90°
(
)
∠2+∠1=90°
∠3+∠4=∠4+∠5
∴∠1=∠D
(
)
∠3=∠5
在△ABC和△DEC中
∠1=∠D
(
)
∠
=∠
(已证)
=
(已知)
∴△ABC≌△DEC
(
)(用字母表示)
(2)若∠3=30°,则∠B=
度.(直接填空)
23.如图,在△ABC中,∠BAC=90°,AB=6,AC=8,BC=10,若AD平分∠BAC交BC于点D,求BD的长.
24.如图所示,A,C,E三点在同一直线上,且△ABC≌△DAE.
(1)求证:BC=DE+CE;
(2)当△ABC满足什么条件时,BC∥DE?
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.解:A、∵△ABC≌△ADE,
∴∠ABC=∠AED,但∠ABC与∠AED不一定相等,本选项结论不成立,不符合题意;
B、∵△ABC≌△ADE,
∴∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE,本选项结论成立,符合题意;
C、∵△ABC≌△ADE,
∴AB=AD,AB与AE不一定相等,本选项结论不成立,不符合题意;
D、∵△ABC≌△ADE,
∴AC=AE,AC与DE不一定相等,本选项结论不成立,不符合题意;
故选:B.
2.解:如果AM=AN,
在△ABM和△ACN中,
,
∴△ABM≌△ACN(AAS).
如果AB=AC,
在△ABM和△ACN中,
,
∴△ABM≌△ACN(ASA).
如果BM=CN,
在△ABM和△ACN中,
,
∴△ABM≌△ACN(ASA).
只有D选项不满足题意,
故选:D.
3.解:∵AD平分∠BAC,
∴∠EAD=∠FAD,
在△ADE与△ADF中,
,
∴△ADE≌△ADF(SAS),
故选:C.
4.解:①当点P在正方形的边AB上时,
在Rt△OCD和Rt△AOP中,
,
∴Rt△OCD≌Rt△AOP(HL),
∴OD=AP,
∵点D是OA中点,
∴OD=AD=OA,
∴AP=AB=2,
∴P(4,2),
②当点P在正方形的边BC上时,
同①的方法,得出CP=BC=2,
∴P(2,4),
∴P(2,4)或(4,2).
故选:D.
5.解:因为第③块中有完整的两个角以及他们的夹边,利用ASA易证三角形全等,故应带第3块.
故选:C.
6.解:过D点作DE⊥AB于E,如图,
∵BC=15,BD=10,
∴CD=BC﹣BD=5,
∵AD平分∠BAC,DC⊥AC,DE⊥AB,
∴DE=DC=5,
∴点D到AB的距离为5.
故选:D.
7.解:尺规作图所用的作图工具是指不带刻度的直尺和圆规,
故选:D.
8.解:∵△ABC≌△ADE,
∴AB=AD;∠E=∠C;BC=DE,∠BAC=∠DAE,
∴∠BAC﹣∠BAD=∠DAE﹣∠DAC,
即∠BAD=∠CAE,
∵∠BAE=120°,∠BAD=40°,
∴∠CAE=40°,
∴∠BAC=∠BAE﹣∠CAE=80°,
∴①②③④都正确,
故选:D.
9.解:①两个锐角分别相等的的两个直角三角形不一定全等,故该说法错误;
②如图,已知:∠B=∠E=90°,BC=EF,AM=BM,DN=EN,CM=FN,
求证:△ABC≌△DEF,
证明:∵∠B=∠E=90°,BC=EF,CM=FN,
∴Rt△BCM≌Rt△EFN(HL),
∴BM=EN
∵AM=BM,DN=EN,
∴AB=DE,
∴Rt△ABC≌Rt△EFN(SAS),
故一条直角边相等且另一条直角边上的中线相等的两个直角三角形全等的说法正确;
③两对应边分别相等的两个直角三角形全等,如果是一个直角三角形的两条直角边和另一个直角三角形的一条直角边和一条斜边分别相等,这两个直角三角形不全等,故该说法错误;
④一个锐角和一条边分别对应相等的两个直角三角形不一定全等,如果一个直角三角形的一条直角边和另一个直角三角形的一条斜边相等,这两个直角三角形不全等,故该说法错误;故选:A.
10.解:连接AB.
在△AOB和△DOC中,
,
∴△AOB≌△DOC(SAS),
∴AB=CD=a,
∵EF=b,
∴圆柱形容器的壁厚是(b﹣a),
故选:D.
二.填空题(共7小题,满分21分,每小题3分)
11.解:在△OCF与△ODG中,,
∴△OCF≌△ODG(AAS),
∴CF=DG=40,
∴小明离地面的高度是50+40=90,
故答案为:90.
12.解:连接AB,A′B′,如图,
∵点O分别是AA′、BB′的中点,
∴OA=OA′,OB=OB′,
在△AOB和△A′OB′中,
,
∴△AOB≌△A′OB′(SAS).
∴A′B′=AB.
答:需要测量A′B′的长度,即为工件内槽宽AB.
其依据是根据SAS证明△AOB≌△A′OB′;
故答案为:根据SAS证明△AOB≌△A′OB′.
13.解:∵∠B=70°,∠ACB=30°,
∴∠A=180°﹣∠B﹣∠ACB=80°,
∵△ABC≌△DFE,
∴∠D=∠A=80°,
故答案为:80.
14.解:如图,作CD∥AB,连接DE,
则∠2=∠3,∠4=∠5,
设每个小正方形的边长为a,
则CD=a,DE=a,CE=a,
∵CD2+DE2=(a)2+(a)2=10a2=CE2,CD=DE,
∴△CDE是等腰直角三角形,∠CDE=90°,
∴∠DEC=45°,∠3+∠4=90°,
∴∠2﹣∠1=∠3﹣∠1
=90°﹣∠4﹣∠1
=90°﹣∠5﹣∠1
=90°﹣(45°﹣∠1)﹣∠1
=45°,
故答案为:45°.
15.解:如图,作OD⊥AB于D,OE⊥AC于E,OF⊥BC于F,
∵三条角平分线交于点O,OD⊥BC,OE⊥AC,OF⊥AB,
∴OD=OE=OF,
∵△ABC的三边AB、BC、CA的长分别为30,40,50,
∴S△ABO:S△BCO:S△CAO=AB:BC:CA=3:4:5,
故答案为:3:4:5.
16.解:∵∠CMD=90°,
∴∠CMA+∠DMB=90°,
又∵∠CAM=90°,
∴∠CMA+∠C=90°,
∴∠C=∠DMB.
在Rt△ACM和Rt△BMD中,
,
∴Rt△ACM≌Rt△BMD(AAS),
∴BD=AM=12米,
∴BM=20﹣12=8(米),
∵该人的运动速度为2m/s,
∴他到达点M时,运动时间为8÷2=4(s).
故答案为4.
17.解:如图,过点D作DM⊥BE于点M,DN⊥AC于点N,DG⊥BA于点G.
∵CD平分∠ACE,DM⊥BE于M,DN⊥AC于N,
∴DM=DN,∠DCE=.
∴∠DCE=∠BDC+∠DBC=.
∴∠BDC=.
∵BD平分∠ABC,DM⊥BE于M,DG⊥BA于G,
∴DM=DG,∠DBC=.
∴DG=DN,∠BDC=﹣∠DBC=.
∴∠BDC=.
又∵∠BDC=24°,
∴∠BAC=48°.
∴∠CAG=180°﹣∠BAC=132°.
在Rt△ADG和Rt△ADN中,
∴Rt△ADG≌Rt△ADN(HL).
∴∠GAD=∠NAD.
∠DAN==66°,即∠CAD=66°.
故答案为:66°.
三.解答题(共7小题,满分49分)
18.证明:如图,在Rt△ACE和Rt△CBF中,
,
∴Rt△ACE≌Rt△CBF(HL),
∴∠EAC=∠BCF,
∵∠EAC+∠ACE=90°,
∴∠ACE+∠BCF=90°,
∴∠ACB=180°﹣90°=90°.
19.证明:∵∠E=∠C(已知),
∠AFE=∠DFC
(对顶角相等),
∴∠2=∠3
(三角形内角和是180°).
∵∠1=∠2(等量代换),
∴∠1+∠DAC=∠2+∠DAC
(等式的基本性质).
即∠BAC=∠DAE.
在△ABC和△ADE中,
∵,
∴△ABC≌△ADE
(ASA).
故答案为:对顶角相等;三角形内角和是180°;等式的基本性质;ASA.
20.(1)证明:∵∠1=∠2,
∴ED=CE,
∵∠A=∠B=90°,
在Rt△ADE和Rt△BEC中,
,
∴Rt△ADE≌Rt△BEC(HL);
(2)解:△CDE是直角三角形,理由如下:
证明:由(1)得Rt△ADE≌Rt△BEC,
∴∠AED=∠BCE,
∵∠B=90°,
∴∠BCE+∠CEB=90°,
∴∠AED+∠CEB=90°,
∴∠DEC=180°﹣90°=90°,
∴△DEC为直角三角形.
21.(1)证明:由题意得:AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,
∴∠ADC=∠CEB=90°,
∴∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,
∴∠BCE=∠DAC
在△ADC和△CEB中,
∴△ADC≌△CEB(AAS);
(2)解:由题意得:AD=2×3=6cm,BE=7×2=14cm,
∵△ADC≌△CEB,
∴EC=AD=6cm,DC=BE=14cm,
∴DE=DC+CE=20(cm),
答:两堵木墙之间的距离为20cm.
22.解:(1)根据∠ACD=90°可知△ACD是直角三角形,
∴∠2+∠D=90°的理由为直角三角形的两锐角互余,
故答案为:直角三角形的两锐角互余.
再根据∠1+∠2=90°可得∠1=∠D的理由为同角的余角相等,
故答案为:同角的余角相等.
∴在证明△ABC和△DEC全等时,
∠1=∠D,是前面已经证明的结论,故此处的理由应该是已证,
故答案为:已证.
根据括号中的提示和三角形全等要用的条件,
可知应该填的内容为∠3=∠5,BC=EC,
故答案为:3,5,BC,EC.
∴三角形的全等的证明方法为AAS,
故答案为:AAS.
(2)∵△ABC≌△DEC.
∴AC=DC,
∵∠ACD=90°,
∴△ACD为等腰直角三角形,
∴∠D=45°=∠1,
∵∠3=30°,
∴∠B=180°﹣30°﹣45°=105°.
23.解:过A点作AH⊥BC于H,过D点作DE⊥AB于E,DF⊥AC于F,如图,
∵AH?BC=AC?AB,
∴AH==,
∵AD平分∠BAC,
∴DE=DF,
∵AB?DE+AC?DF=AB?AC,
∴3DE+4DF=24,
∴DE=,
∵S△ABD=AH?BD=AB?DE,
∴BD==.
24.(1)证明:∵△ABC≌△DAE,
∴AE=BC,AC=DE,
又∵AE=AC+CE,
∴BC=DE+CE;
(2)解:∵BC∥DE,
∴∠BCE=∠E,
又∵△ABC≌△DAE,
∴∠ACB=∠E,
∴∠ACB=∠BCE,
又∵∠ACB+∠BCE=180°,
∴∠ACB=90°,
即当△ABC满足∠ACB为直角时,BC∥DE.
专题突破训练(附答案)
一.选择题(共10小题,满分30分,每小题3分)
1.如图,若△ABC≌△ADE,则下列结论中一定成立的是( )
A.∠ABC=∠AED
B.∠BAD=∠CAE
C.AB=AE
D.AC=DE
2.如图,已知点M,N分别在AC,AB上,∠MBN=∠MCN,现添加下面的哪一个条件后,仍不能判定△ABM≌△ACN的是( )
A.AM=AN
B.AB=AC
C.BM=CN
D.∠AMB=∠ANC
3.如图,在△ABC中,AD平分∠BAC,且AE=AF,则可直接用“SAS”判断的是( )
A.△ABD≌△ACD
B.△BDE≌△CDF
C.△ADE≌△ADF
D.△ABD≌△ABC
4.如图,点B的坐标为(4,4),作BA⊥x轴,BC⊥y轴,垂足分别为A、C,点D为线段OA的中点,点P从点A出发,在线段AB、BC上沿A→B→C运动,当OP=CD时,点P的坐标为( )
A.(4,1)
B.(4,2)
C.(2,2)
D.(4,2)或(2,4)
5.一块三角形玻璃,被摔成如图所示的四块,小敏想去店里买一块形状、大小与原来一样的玻璃,借助“全等三角形”的相关知识,小敏只带了一块去,则这块玻璃的编号是( )
A.①
B.②
C.③
D.④
6.如图,在Rt△ACB中,∠C=90°,AD平分∠BAC,若BC=15,BD=10,则点D到AB的距离是( )
A.15
B.10
C.8
D.5
7.尺规作图是指( )
A.用直尺和圆规作图
B.用直尺规范作图
C.用刻度尺和圆规作图
D.用没有刻度的直尺和圆规作图
8.如图,△ABC≌△ADE,则下列结论正确的个数是( )
①AB=AD;②∠E=∠C;③若∠BAE=120°,∠BAD=40°,则∠BAC=80°;④BC=DE.
A.1
B.2
C.3
D.4
9.下列说法正确的有( )
①两个锐角分别相等的的两个直角三角形全等;
②一条直角边相等且另一条直角边上的中线相等的两个直角三角形全等;
③两边分别相等的两个直角三角形全等;
④一个锐角和一条边分别相等的两个直角三角形全等.
A.1
B.2
C.3
D.4
10.在测量一个小口圆形容器的壁厚时,小明用“X型转动钳”按如图方法进行测量,其中OA=OD,OB=OC,测得AB=a,EF=b,圆形容器的壁厚是( )
A.a
B.b
C.b﹣a
D.(b﹣a)
二.填空题(共7小题,满分21分,每小题3分)
11.如图,小明与小红玩跷跷板游戏,如果跷跷板的支点O(即跷跷板的中点)至地面的距离是50cm,当小红从水平位置CD下降40cm时,这时小明离地面的高度是
cm.
12.如图,把两根钢条的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳),在图中,要测量工件内槽宽AB,只要测量A′B′的长度即可,该做法的依据是
.
13.如图,△ABC≌△DFE,∠B=70°,∠ACB=30°,则∠D=
°.
14.如图,在3×3的正方形网格中标出了∠1和∠2,则∠2﹣∠1=
°.
15.如图,△ABC的三边AB、BC、CA的长分别为30,40,50其三条角平分线交于点O,则S△ABO:S△BCO:S△CAO=
.
16.如图,两根旗杆间相距20米,某人从点B沿BA走向点A,一段时间后他到达点M,此时他分别仰望旗杆的顶点C和D,两次视线的夹角为90°,且CM=DM.已知旗杆BD的高为12米,该人的运动速度为2米/秒,则这个人运动到点M所用时间是
秒.
17.如图,△ABC中,一内角和一外角的平分线交于点D,连结AD,∠BDC=24°,∠CAD=
.
三.解答题(共7小题,满分49分)
18.如图,在△ABC中,AC=BC,直线l经过顶点C,过A,B两点分别作l的垂线AE,BF,E,F为垂足,AE=CF.求证:∠ACB=90°.
19.完成下列推理过程.
如图所示,点E在△ABC外部,点D在BC边上,DE交AC于F,若∠1=∠3,∠E=∠C,AE=AC,求证:△ABC≌△ADE.
证明:∵∠E=∠C(已知),
∠AFE=∠DFC
(
),
∴∠2=∠3
(
).
∵∠1=∠2(等量代换),
∴∠1+∠DAC=∠2+∠DAC
(
).
即∠BAC=∠DAE.
在△ABC和△ADE中,
∵,
∴△ABC≌△ADE
(
).
20.如图,∠A=∠B=90°,E是AB上的一点,且AE=BC,∠1=∠2.
(1)求证:Rt△ADE≌Rt△BEC;
(2)△CDE是不是直角三角形?并说明理由.
21.王强同学用10块高度都是2cm的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC=BC,∠ACB=90°),点C在DE上,点A和B分别与木墙的顶端重合.
(1)求证:△ADC≌△CEB;
(2)求两堵木墙之间的距离.
22.按逻辑填写步骤和理由,将下面的证明过程补充完整.
如图,四边形ABCD中,E点在AD上,∠BAE=∠BCE=∠ACD=90°,BC=EC.
(1)求证:△ABC≌△DEC.
证明:
∵∠BAE=∠BCE=∠ACD=90°(已知)
∴∠2+∠D=90°
(
)
∠2+∠1=90°
∠3+∠4=∠4+∠5
∴∠1=∠D
(
)
∠3=∠5
在△ABC和△DEC中
∠1=∠D
(
)
∠
=∠
(已证)
=
(已知)
∴△ABC≌△DEC
(
)(用字母表示)
(2)若∠3=30°,则∠B=
度.(直接填空)
23.如图,在△ABC中,∠BAC=90°,AB=6,AC=8,BC=10,若AD平分∠BAC交BC于点D,求BD的长.
24.如图所示,A,C,E三点在同一直线上,且△ABC≌△DAE.
(1)求证:BC=DE+CE;
(2)当△ABC满足什么条件时,BC∥DE?
参考答案
一.选择题(共10小题,满分30分,每小题3分)
1.解:A、∵△ABC≌△ADE,
∴∠ABC=∠AED,但∠ABC与∠AED不一定相等,本选项结论不成立,不符合题意;
B、∵△ABC≌△ADE,
∴∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE,本选项结论成立,符合题意;
C、∵△ABC≌△ADE,
∴AB=AD,AB与AE不一定相等,本选项结论不成立,不符合题意;
D、∵△ABC≌△ADE,
∴AC=AE,AC与DE不一定相等,本选项结论不成立,不符合题意;
故选:B.
2.解:如果AM=AN,
在△ABM和△ACN中,
,
∴△ABM≌△ACN(AAS).
如果AB=AC,
在△ABM和△ACN中,
,
∴△ABM≌△ACN(ASA).
如果BM=CN,
在△ABM和△ACN中,
,
∴△ABM≌△ACN(ASA).
只有D选项不满足题意,
故选:D.
3.解:∵AD平分∠BAC,
∴∠EAD=∠FAD,
在△ADE与△ADF中,
,
∴△ADE≌△ADF(SAS),
故选:C.
4.解:①当点P在正方形的边AB上时,
在Rt△OCD和Rt△AOP中,
,
∴Rt△OCD≌Rt△AOP(HL),
∴OD=AP,
∵点D是OA中点,
∴OD=AD=OA,
∴AP=AB=2,
∴P(4,2),
②当点P在正方形的边BC上时,
同①的方法,得出CP=BC=2,
∴P(2,4),
∴P(2,4)或(4,2).
故选:D.
5.解:因为第③块中有完整的两个角以及他们的夹边,利用ASA易证三角形全等,故应带第3块.
故选:C.
6.解:过D点作DE⊥AB于E,如图,
∵BC=15,BD=10,
∴CD=BC﹣BD=5,
∵AD平分∠BAC,DC⊥AC,DE⊥AB,
∴DE=DC=5,
∴点D到AB的距离为5.
故选:D.
7.解:尺规作图所用的作图工具是指不带刻度的直尺和圆规,
故选:D.
8.解:∵△ABC≌△ADE,
∴AB=AD;∠E=∠C;BC=DE,∠BAC=∠DAE,
∴∠BAC﹣∠BAD=∠DAE﹣∠DAC,
即∠BAD=∠CAE,
∵∠BAE=120°,∠BAD=40°,
∴∠CAE=40°,
∴∠BAC=∠BAE﹣∠CAE=80°,
∴①②③④都正确,
故选:D.
9.解:①两个锐角分别相等的的两个直角三角形不一定全等,故该说法错误;
②如图,已知:∠B=∠E=90°,BC=EF,AM=BM,DN=EN,CM=FN,
求证:△ABC≌△DEF,
证明:∵∠B=∠E=90°,BC=EF,CM=FN,
∴Rt△BCM≌Rt△EFN(HL),
∴BM=EN
∵AM=BM,DN=EN,
∴AB=DE,
∴Rt△ABC≌Rt△EFN(SAS),
故一条直角边相等且另一条直角边上的中线相等的两个直角三角形全等的说法正确;
③两对应边分别相等的两个直角三角形全等,如果是一个直角三角形的两条直角边和另一个直角三角形的一条直角边和一条斜边分别相等,这两个直角三角形不全等,故该说法错误;
④一个锐角和一条边分别对应相等的两个直角三角形不一定全等,如果一个直角三角形的一条直角边和另一个直角三角形的一条斜边相等,这两个直角三角形不全等,故该说法错误;故选:A.
10.解:连接AB.
在△AOB和△DOC中,
,
∴△AOB≌△DOC(SAS),
∴AB=CD=a,
∵EF=b,
∴圆柱形容器的壁厚是(b﹣a),
故选:D.
二.填空题(共7小题,满分21分,每小题3分)
11.解:在△OCF与△ODG中,,
∴△OCF≌△ODG(AAS),
∴CF=DG=40,
∴小明离地面的高度是50+40=90,
故答案为:90.
12.解:连接AB,A′B′,如图,
∵点O分别是AA′、BB′的中点,
∴OA=OA′,OB=OB′,
在△AOB和△A′OB′中,
,
∴△AOB≌△A′OB′(SAS).
∴A′B′=AB.
答:需要测量A′B′的长度,即为工件内槽宽AB.
其依据是根据SAS证明△AOB≌△A′OB′;
故答案为:根据SAS证明△AOB≌△A′OB′.
13.解:∵∠B=70°,∠ACB=30°,
∴∠A=180°﹣∠B﹣∠ACB=80°,
∵△ABC≌△DFE,
∴∠D=∠A=80°,
故答案为:80.
14.解:如图,作CD∥AB,连接DE,
则∠2=∠3,∠4=∠5,
设每个小正方形的边长为a,
则CD=a,DE=a,CE=a,
∵CD2+DE2=(a)2+(a)2=10a2=CE2,CD=DE,
∴△CDE是等腰直角三角形,∠CDE=90°,
∴∠DEC=45°,∠3+∠4=90°,
∴∠2﹣∠1=∠3﹣∠1
=90°﹣∠4﹣∠1
=90°﹣∠5﹣∠1
=90°﹣(45°﹣∠1)﹣∠1
=45°,
故答案为:45°.
15.解:如图,作OD⊥AB于D,OE⊥AC于E,OF⊥BC于F,
∵三条角平分线交于点O,OD⊥BC,OE⊥AC,OF⊥AB,
∴OD=OE=OF,
∵△ABC的三边AB、BC、CA的长分别为30,40,50,
∴S△ABO:S△BCO:S△CAO=AB:BC:CA=3:4:5,
故答案为:3:4:5.
16.解:∵∠CMD=90°,
∴∠CMA+∠DMB=90°,
又∵∠CAM=90°,
∴∠CMA+∠C=90°,
∴∠C=∠DMB.
在Rt△ACM和Rt△BMD中,
,
∴Rt△ACM≌Rt△BMD(AAS),
∴BD=AM=12米,
∴BM=20﹣12=8(米),
∵该人的运动速度为2m/s,
∴他到达点M时,运动时间为8÷2=4(s).
故答案为4.
17.解:如图,过点D作DM⊥BE于点M,DN⊥AC于点N,DG⊥BA于点G.
∵CD平分∠ACE,DM⊥BE于M,DN⊥AC于N,
∴DM=DN,∠DCE=.
∴∠DCE=∠BDC+∠DBC=.
∴∠BDC=.
∵BD平分∠ABC,DM⊥BE于M,DG⊥BA于G,
∴DM=DG,∠DBC=.
∴DG=DN,∠BDC=﹣∠DBC=.
∴∠BDC=.
又∵∠BDC=24°,
∴∠BAC=48°.
∴∠CAG=180°﹣∠BAC=132°.
在Rt△ADG和Rt△ADN中,
∴Rt△ADG≌Rt△ADN(HL).
∴∠GAD=∠NAD.
∠DAN==66°,即∠CAD=66°.
故答案为:66°.
三.解答题(共7小题,满分49分)
18.证明:如图,在Rt△ACE和Rt△CBF中,
,
∴Rt△ACE≌Rt△CBF(HL),
∴∠EAC=∠BCF,
∵∠EAC+∠ACE=90°,
∴∠ACE+∠BCF=90°,
∴∠ACB=180°﹣90°=90°.
19.证明:∵∠E=∠C(已知),
∠AFE=∠DFC
(对顶角相等),
∴∠2=∠3
(三角形内角和是180°).
∵∠1=∠2(等量代换),
∴∠1+∠DAC=∠2+∠DAC
(等式的基本性质).
即∠BAC=∠DAE.
在△ABC和△ADE中,
∵,
∴△ABC≌△ADE
(ASA).
故答案为:对顶角相等;三角形内角和是180°;等式的基本性质;ASA.
20.(1)证明:∵∠1=∠2,
∴ED=CE,
∵∠A=∠B=90°,
在Rt△ADE和Rt△BEC中,
,
∴Rt△ADE≌Rt△BEC(HL);
(2)解:△CDE是直角三角形,理由如下:
证明:由(1)得Rt△ADE≌Rt△BEC,
∴∠AED=∠BCE,
∵∠B=90°,
∴∠BCE+∠CEB=90°,
∴∠AED+∠CEB=90°,
∴∠DEC=180°﹣90°=90°,
∴△DEC为直角三角形.
21.(1)证明:由题意得:AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,
∴∠ADC=∠CEB=90°,
∴∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,
∴∠BCE=∠DAC
在△ADC和△CEB中,
∴△ADC≌△CEB(AAS);
(2)解:由题意得:AD=2×3=6cm,BE=7×2=14cm,
∵△ADC≌△CEB,
∴EC=AD=6cm,DC=BE=14cm,
∴DE=DC+CE=20(cm),
答:两堵木墙之间的距离为20cm.
22.解:(1)根据∠ACD=90°可知△ACD是直角三角形,
∴∠2+∠D=90°的理由为直角三角形的两锐角互余,
故答案为:直角三角形的两锐角互余.
再根据∠1+∠2=90°可得∠1=∠D的理由为同角的余角相等,
故答案为:同角的余角相等.
∴在证明△ABC和△DEC全等时,
∠1=∠D,是前面已经证明的结论,故此处的理由应该是已证,
故答案为:已证.
根据括号中的提示和三角形全等要用的条件,
可知应该填的内容为∠3=∠5,BC=EC,
故答案为:3,5,BC,EC.
∴三角形的全等的证明方法为AAS,
故答案为:AAS.
(2)∵△ABC≌△DEC.
∴AC=DC,
∵∠ACD=90°,
∴△ACD为等腰直角三角形,
∴∠D=45°=∠1,
∵∠3=30°,
∴∠B=180°﹣30°﹣45°=105°.
23.解:过A点作AH⊥BC于H,过D点作DE⊥AB于E,DF⊥AC于F,如图,
∵AH?BC=AC?AB,
∴AH==,
∵AD平分∠BAC,
∴DE=DF,
∵AB?DE+AC?DF=AB?AC,
∴3DE+4DF=24,
∴DE=,
∵S△ABD=AH?BD=AB?DE,
∴BD==.
24.(1)证明:∵△ABC≌△DAE,
∴AE=BC,AC=DE,
又∵AE=AC+CE,
∴BC=DE+CE;
(2)解:∵BC∥DE,
∴∠BCE=∠E,
又∵△ABC≌△DAE,
∴∠ACB=∠E,
∴∠ACB=∠BCE,
又∵∠ACB+∠BCE=180°,
∴∠ACB=90°,
即当△ABC满足∠ACB为直角时,BC∥DE.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
