勾股定理
图片预览

文档简介
(共36张PPT)
1
2
3
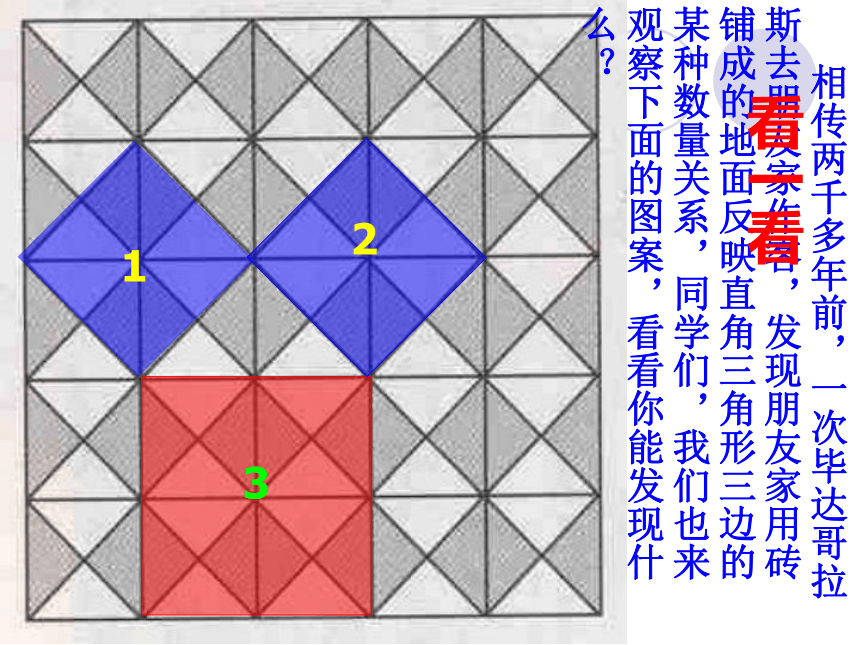
相传两千多年前,一次毕达哥拉斯去朋友家作客,发现朋友家用砖铺成的地面反映直角三角形三边的某种数量关系,同学们,我们也来观察下面的图案,看看你能发现什么?
看一看
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图2-1
图2-2
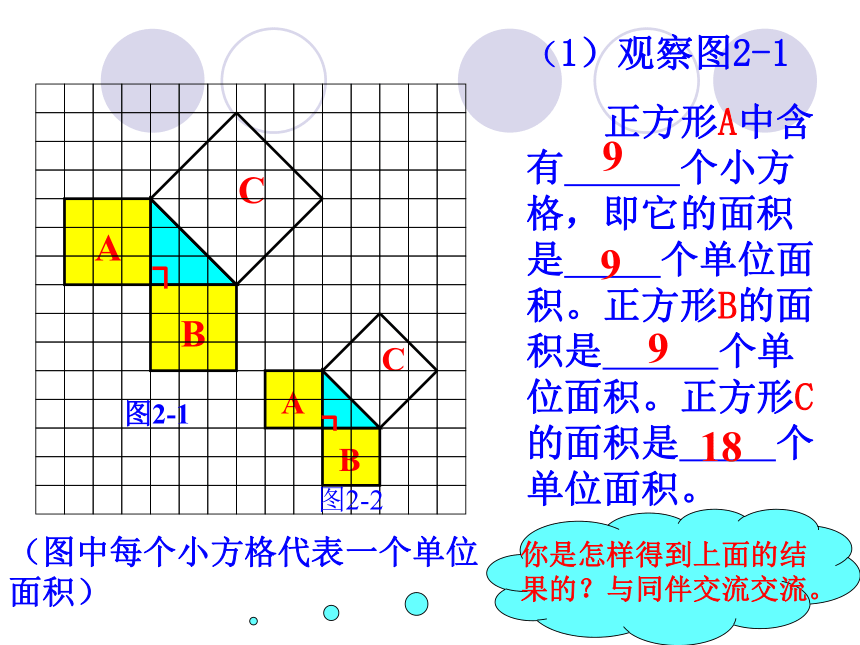
(1)观察图2-1
正方形A中含有 个小方格,即它的面积是 个单位面积。正方形B的面积是 个单位面积。正方形C的面积是 个单位面积。
9
9
9
18
你是怎样得到上面的结果的?与同伴交流交流。
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图1-1
图1-2
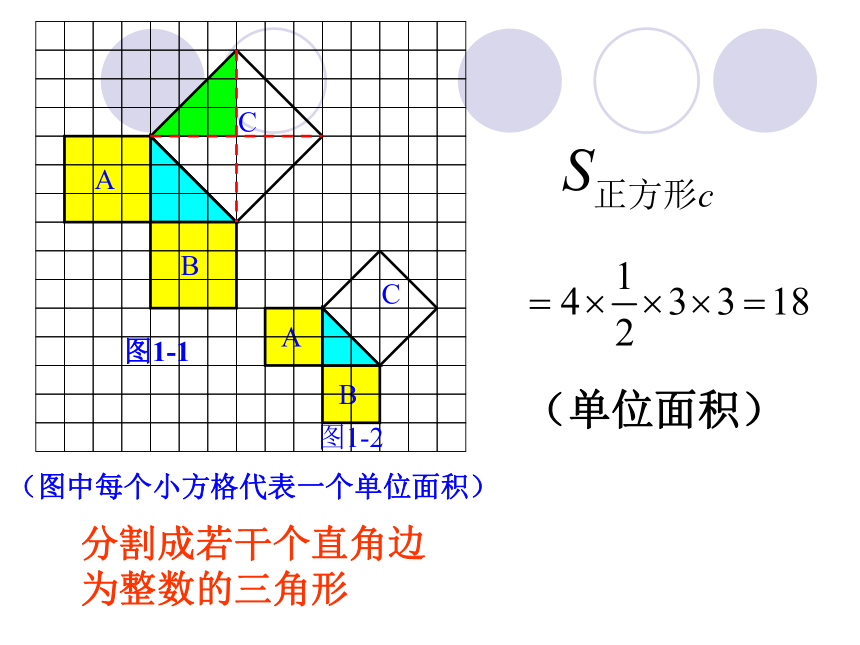
分割成若干个直角边为整数的三角形
(单位面积)
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图1-1
图1-2
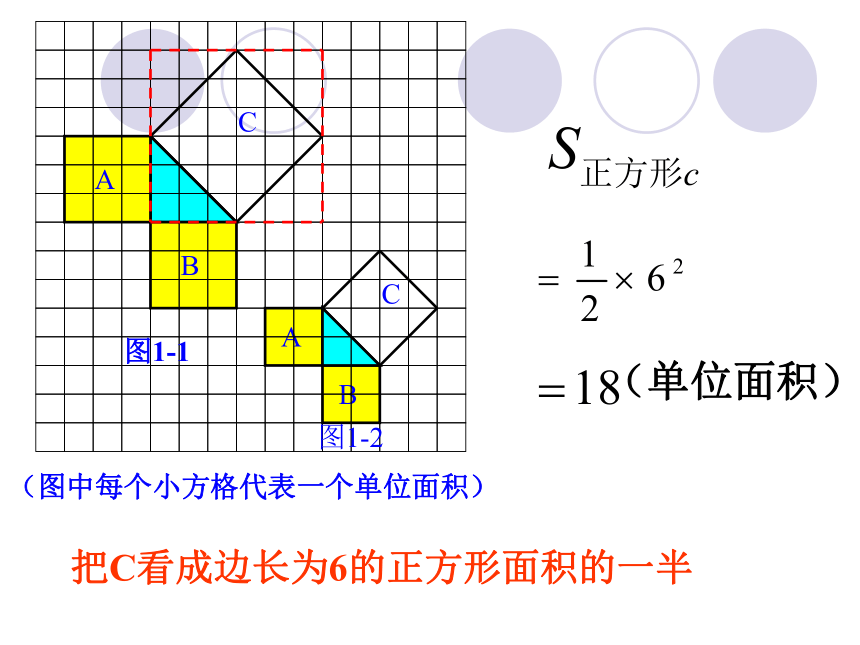
(单位面积)
把C看成边长为6的正方形面积的一半
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图2-1
图2-2
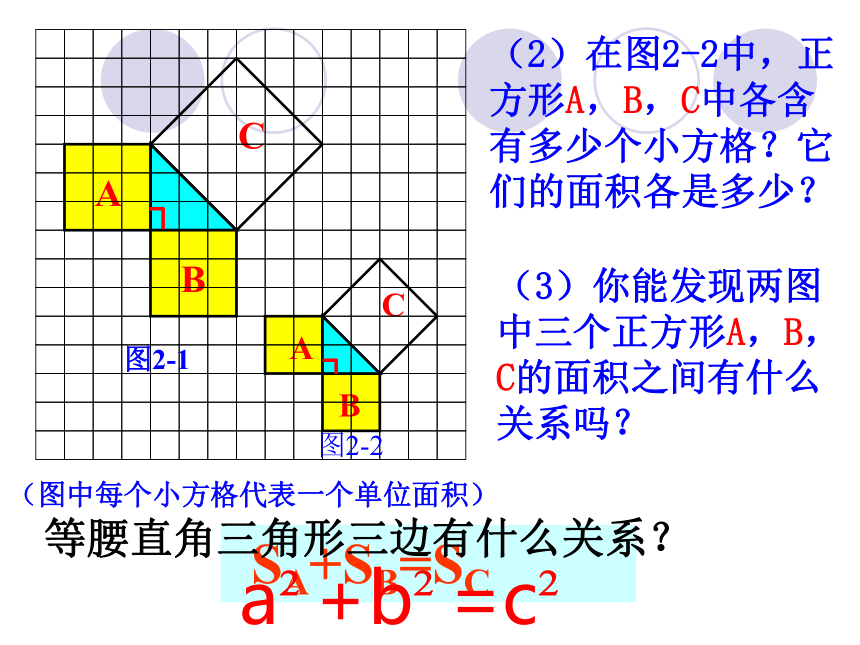
(2)在图2-2中,正方形A,B,C中各含有多少个小方格?它们的面积各是多少?
(3)你能发现两图中三个正方形A,B,C的面积之间有什么关系吗?
SA+SB=SC
等腰直角三角形三边有什么关系?
a +b =c
P
Q
C
R
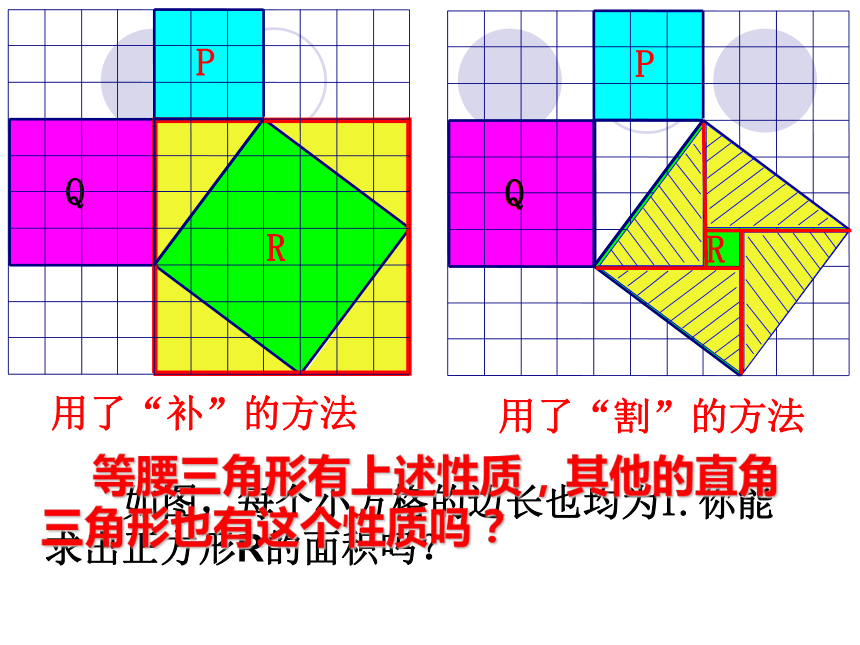
如图,每个小方格的边长也均为1.你能求出正方形R的面积吗?
(1)
用了“补”的方法
P
Q
C
R
用了“割”的方法
Q
等腰三角形有上述性质,其他的直角三角形也有这个性质吗?
P
Q
R
a
c
b
SP+SQ=SR
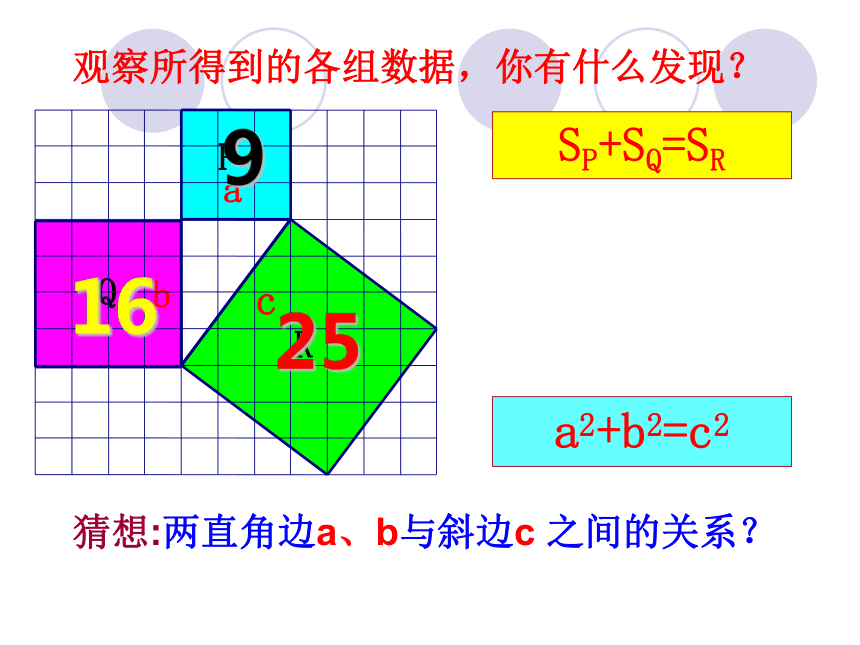
观察所得到的各组数据,你有什么发现?
猜想:两直角边a、b与斜边c 之间的关系?
a2+b2=c2
16
9
25
a
c
b
SP+SQ=SR
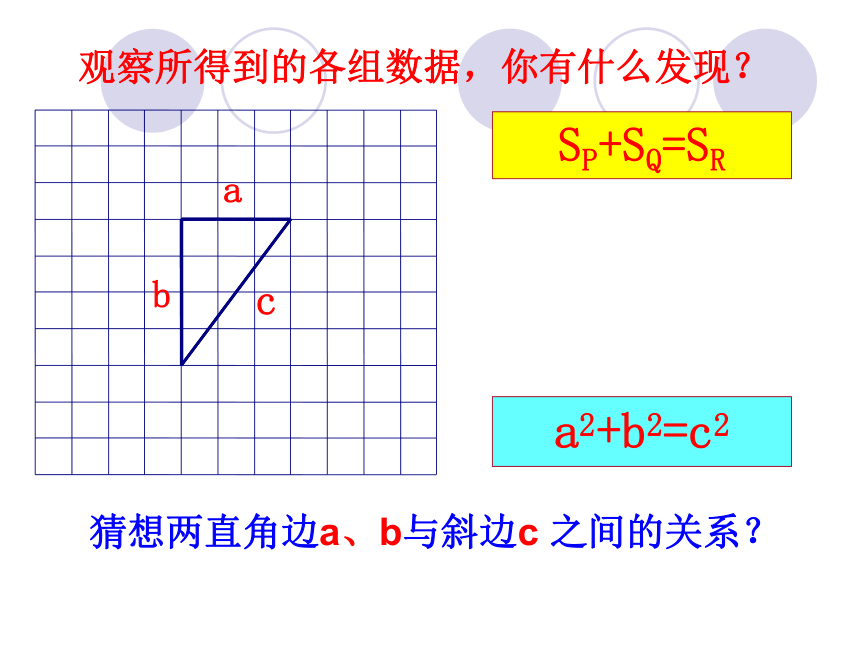
观察所得到的各组数据,你有什么发现?
猜想两直角边a、b与斜边c 之间的关系?
a2+b2=c2
┏
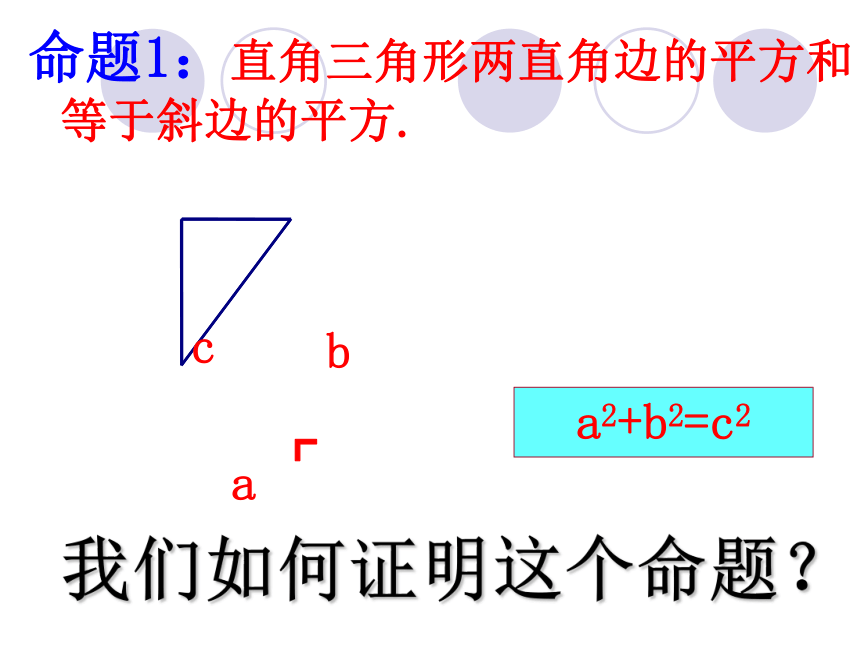
a2+b2=c2
a
c
b
命题1:直角三角形两直角边的平方和等于斜边的平方.
我们如何证明这个命题?
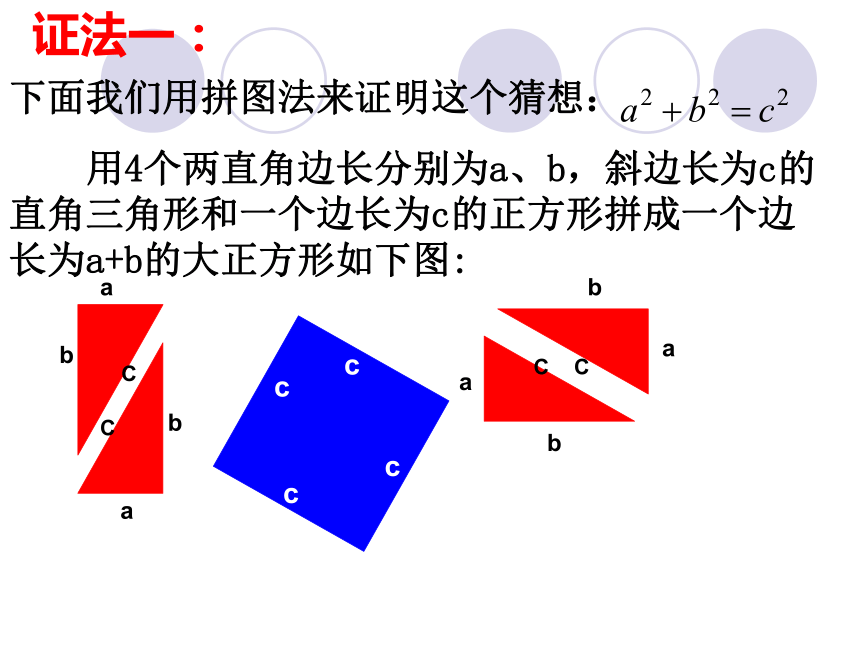
下面我们用拼图法来证明这个猜想:
用4个两直角边长分别为a、b,斜边长为c的直角三角形和一个边长为c的正方形拼成一个边长为a+b的大正方形如下图:
a
b
a
b
a
b
a
b
c
c
c
c
C
C
C
C
证法一:
a
a
a
a
b
b
b
b
c
c
c
c
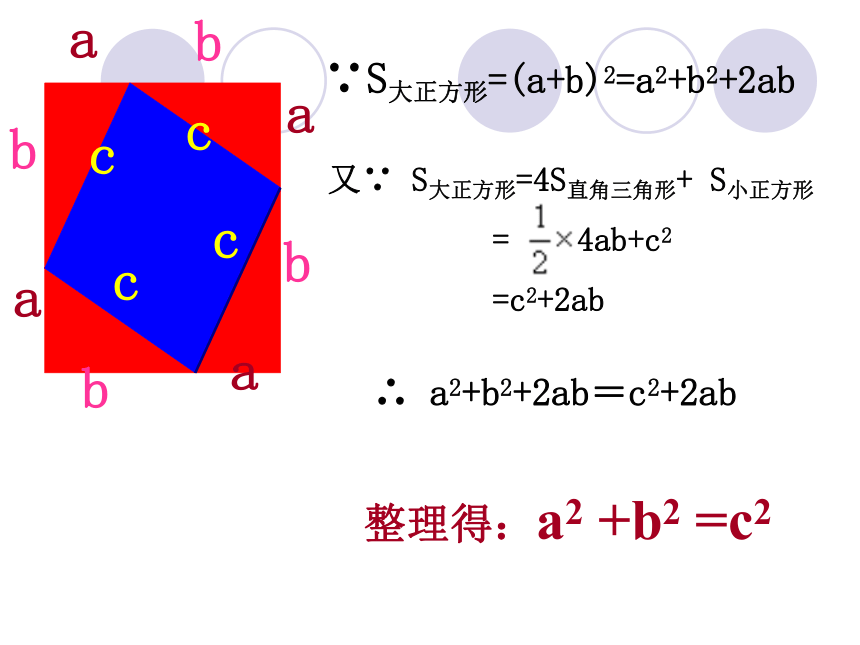
又∵ S大正方形=4S直角三角形+ S小正方形
= 4ab+c2
=c2+2ab
整理得:a2 +b2 =c2
∴ a2+b2+2ab=c2+2ab
∵S大正方形=(a+b)2=a2+b2+2ab
用赵爽弦图证明
证法二:
a
b
c
∴a2+b2=c2
a
a
b
b
c
c
证法三、美国第20任总统伽菲尔德证法:
∵ s梯形= (a+b)(a+b)= (a2+2ab+b2)
s梯形=2× ab+ c2=ab+ c2
∴ a2+ab+ b2=ab+ c2
∴a2+b2=c2
= a2+ab+ b2
证法四:毕达哥拉斯证法:
a
b
c
a
a
b
b
c
S大正方形=4× ab+a2+b2
=2ab+a2+b2
S大正方形=4× ab+c2
=2ab+c2
∵S大正方形=S大正方形
∴2ab+a2+b2=2ab+c2
∴a2+b2=c2
┏
a2+b2=c2
a
c
b
直角三角形两直角边的平方和等于斜边的平方.
勾
股
弦
勾股定理:
我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦
结论变形:
c2 = a2 + b2
a
b
c
A
B
C
a2 = c2-b2
b2 = c2-a2
勾 股 世 界
毕达哥拉斯
(公元前572----前492年),
古希腊著名的哲学家、数学家、天文学家。
两千多年前,古希腊有个毕达哥拉斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派,1955年希腊曾经发行了一枚纪念邮票。
在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”.所以古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.因此就把这一定理称为勾股定理.
勾
股
勾
股
弦
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。
★ 《周髀算经》中还记载了公元前六、七世纪的荣方与陈子的对话,再次提到勾股理。——陈子定理
★ 古巴比仑人在公元前19世纪也发现此定理。具调查在公元前1900年的一块巴比伦上午泥板中,记载了15组勾股数。所以古巴比伦人才是勾股定理最先的发现人。
★ 定理从提出到现在的两千多年中,已经找到证明400多种,由鲁密斯搜集整理的《毕达哥拉斯》一书中就给出370种不同证法。
★勾股定理又称商高定理、毕达哥拉斯定理
百牛定理、 驴桥定理、
埃及三角形定理
学以致用:1.求图中字母所代表的正方形的面积。
24
80
A
B
B
400
625
∟
81
144
A
225
225
56
80
结论:
S1+S2+S3+S4=S5+S6 =S7=10
S5=s1+s2=4
S6=s3+s4=6
2、
3、求出下列直角三角形中未知的边.
6
10
A
C
B
8
A
15
C
B
30°
2
2
45°
①在解决上述问题时,每个直角三角形需知道几个条件?
②直角三角形哪条边最长?
8
17
1
两个条件
斜边
方法小结:
可用勾股定理建立方程.
4、在△ABC中, ∠C=90°,a=6,b=8,则c=__
6、在一个直角三角形中, 两边长分别为6、8,
则第三边的长为________
10
10
或
5、一直角三角形的一直角边长为6,斜边长比
另一直角边长大2,则斜边的长为_____。
10
7、在Rt△ABC中,∠C=90°,
①若a=5,b=12,则c=___________;
②若a=15,c=25,则b=___________;
③若c=61,b=60,则a=_______;
④若a∶b=3∶4,c=10则 a=________,b=________。
13
20
11
6
8
补充:如图,分别以直角三角形的三边为直径作三个半圆,这三个半圆的面积之间有什么关系 为什么
S1= ( c )
S2= ( b )
S3= ( a )
∵ a +b =c
∴ S1=S2+S3
c
b
a
S1
S2
S3
说说这节课你有什么收获?
收获与反思
想一想我们这一节课有哪些收获?
1.必做题:习题18.1 第1, 7题。
2.选做题:课本 “阅读与思考”,了解
勾股定理的多种证法。
布置作业:
这棵树漂亮吗?如果在树上挂上几串彩色灯泡,再挂上些小铃铛、小彩球、小礼盒、小的圣诞老人,是不是更像一棵圣诞树.
也许有人会问:“它与勾股定理有什么关系吗?”
仔细看看,你会发现,奥妙在树干和树枝上,整棵树都是由下方的这个基本图形组成的:一个直角三角形以及分别以它的每边为一边向外所作的正方形.
这个图形有什么作用呢?不要小看它哦!古希腊的数学家毕达哥拉斯就是利用这个图形验证了勾股定理.
刘徽在《九章算术》中对勾股定理的证明:勾自乘为朱方,股自乘为青方,令出入相补,各从其类,因就其余不移动也.合成弦方之幂,开方除之,即弦也.
令正方形ABCD为朱方,正方形BEFG为青方.在BG间取一点H,使AH=BG,裁下△ADH,移至△CDI,裁下△HGF,移至△IEF,是为“出入相补,各从其类”,其余不动,则形成弦方正方形DHFI.勾股定理由此得证.
刘徽的证法
返回
a
b
c
①
②
③
④
⑤
证法二 无字证明
青出
朱入
朱出
朱方
青方
青入
青入
青出
青出
证法三、青朱出入图
朱入
朱出
证法六、拼图游戏
又∵这两个正方形的边长都是a+b,所以面积相等,即
⑵
⑴
证明:图1的大正方形的面积为:
图2的大正方形的面积为:
1
2
3
相传两千多年前,一次毕达哥拉斯去朋友家作客,发现朋友家用砖铺成的地面反映直角三角形三边的某种数量关系,同学们,我们也来观察下面的图案,看看你能发现什么?
看一看
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图2-1
图2-2
(1)观察图2-1
正方形A中含有 个小方格,即它的面积是 个单位面积。正方形B的面积是 个单位面积。正方形C的面积是 个单位面积。
9
9
9
18
你是怎样得到上面的结果的?与同伴交流交流。
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图1-1
图1-2
分割成若干个直角边为整数的三角形
(单位面积)
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图1-1
图1-2
(单位面积)
把C看成边长为6的正方形面积的一半
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图2-1
图2-2
(2)在图2-2中,正方形A,B,C中各含有多少个小方格?它们的面积各是多少?
(3)你能发现两图中三个正方形A,B,C的面积之间有什么关系吗?
SA+SB=SC
等腰直角三角形三边有什么关系?
a +b =c
P
Q
C
R
如图,每个小方格的边长也均为1.你能求出正方形R的面积吗?
(1)
用了“补”的方法
P
Q
C
R
用了“割”的方法
Q
等腰三角形有上述性质,其他的直角三角形也有这个性质吗?
P
Q
R
a
c
b
SP+SQ=SR
观察所得到的各组数据,你有什么发现?
猜想:两直角边a、b与斜边c 之间的关系?
a2+b2=c2
16
9
25
a
c
b
SP+SQ=SR
观察所得到的各组数据,你有什么发现?
猜想两直角边a、b与斜边c 之间的关系?
a2+b2=c2
┏
a2+b2=c2
a
c
b
命题1:直角三角形两直角边的平方和等于斜边的平方.
我们如何证明这个命题?
下面我们用拼图法来证明这个猜想:
用4个两直角边长分别为a、b,斜边长为c的直角三角形和一个边长为c的正方形拼成一个边长为a+b的大正方形如下图:
a
b
a
b
a
b
a
b
c
c
c
c
C
C
C
C
证法一:
a
a
a
a
b
b
b
b
c
c
c
c
又∵ S大正方形=4S直角三角形+ S小正方形
= 4ab+c2
=c2+2ab
整理得:a2 +b2 =c2
∴ a2+b2+2ab=c2+2ab
∵S大正方形=(a+b)2=a2+b2+2ab
用赵爽弦图证明
证法二:
a
b
c
∴a2+b2=c2
a
a
b
b
c
c
证法三、美国第20任总统伽菲尔德证法:
∵ s梯形= (a+b)(a+b)= (a2+2ab+b2)
s梯形=2× ab+ c2=ab+ c2
∴ a2+ab+ b2=ab+ c2
∴a2+b2=c2
= a2+ab+ b2
证法四:毕达哥拉斯证法:
a
b
c
a
a
b
b
c
S大正方形=4× ab+a2+b2
=2ab+a2+b2
S大正方形=4× ab+c2
=2ab+c2
∵S大正方形=S大正方形
∴2ab+a2+b2=2ab+c2
∴a2+b2=c2
┏
a2+b2=c2
a
c
b
直角三角形两直角边的平方和等于斜边的平方.
勾
股
弦
勾股定理:
我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦
结论变形:
c2 = a2 + b2
a
b
c
A
B
C
a2 = c2-b2
b2 = c2-a2
勾 股 世 界
毕达哥拉斯
(公元前572----前492年),
古希腊著名的哲学家、数学家、天文学家。
两千多年前,古希腊有个毕达哥拉斯学派,他们首先发现了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。为了纪念毕达哥拉斯学派,1955年希腊曾经发行了一枚纪念邮票。
在中国古代,人们把弯曲成直角的手臂的上半部分称为“勾”,下半部分称为“股”.所以古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.因此就把这一定理称为勾股定理.
勾
股
勾
股
弦
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。
★ 《周髀算经》中还记载了公元前六、七世纪的荣方与陈子的对话,再次提到勾股理。——陈子定理
★ 古巴比仑人在公元前19世纪也发现此定理。具调查在公元前1900年的一块巴比伦上午泥板中,记载了15组勾股数。所以古巴比伦人才是勾股定理最先的发现人。
★ 定理从提出到现在的两千多年中,已经找到证明400多种,由鲁密斯搜集整理的《毕达哥拉斯》一书中就给出370种不同证法。
★勾股定理又称商高定理、毕达哥拉斯定理
百牛定理、 驴桥定理、
埃及三角形定理
学以致用:1.求图中字母所代表的正方形的面积。
24
80
A
B
B
400
625
∟
81
144
A
225
225
56
80
结论:
S1+S2+S3+S4=S5+S6 =S7=10
S5=s1+s2=4
S6=s3+s4=6
2、
3、求出下列直角三角形中未知的边.
6
10
A
C
B
8
A
15
C
B
30°
2
2
45°
①在解决上述问题时,每个直角三角形需知道几个条件?
②直角三角形哪条边最长?
8
17
1
两个条件
斜边
方法小结:
可用勾股定理建立方程.
4、在△ABC中, ∠C=90°,a=6,b=8,则c=__
6、在一个直角三角形中, 两边长分别为6、8,
则第三边的长为________
10
10
或
5、一直角三角形的一直角边长为6,斜边长比
另一直角边长大2,则斜边的长为_____。
10
7、在Rt△ABC中,∠C=90°,
①若a=5,b=12,则c=___________;
②若a=15,c=25,则b=___________;
③若c=61,b=60,则a=_______;
④若a∶b=3∶4,c=10则 a=________,b=________。
13
20
11
6
8
补充:如图,分别以直角三角形的三边为直径作三个半圆,这三个半圆的面积之间有什么关系 为什么
S1= ( c )
S2= ( b )
S3= ( a )
∵ a +b =c
∴ S1=S2+S3
c
b
a
S1
S2
S3
说说这节课你有什么收获?
收获与反思
想一想我们这一节课有哪些收获?
1.必做题:习题18.1 第1, 7题。
2.选做题:课本 “阅读与思考”,了解
勾股定理的多种证法。
布置作业:
这棵树漂亮吗?如果在树上挂上几串彩色灯泡,再挂上些小铃铛、小彩球、小礼盒、小的圣诞老人,是不是更像一棵圣诞树.
也许有人会问:“它与勾股定理有什么关系吗?”
仔细看看,你会发现,奥妙在树干和树枝上,整棵树都是由下方的这个基本图形组成的:一个直角三角形以及分别以它的每边为一边向外所作的正方形.
这个图形有什么作用呢?不要小看它哦!古希腊的数学家毕达哥拉斯就是利用这个图形验证了勾股定理.
刘徽在《九章算术》中对勾股定理的证明:勾自乘为朱方,股自乘为青方,令出入相补,各从其类,因就其余不移动也.合成弦方之幂,开方除之,即弦也.
令正方形ABCD为朱方,正方形BEFG为青方.在BG间取一点H,使AH=BG,裁下△ADH,移至△CDI,裁下△HGF,移至△IEF,是为“出入相补,各从其类”,其余不动,则形成弦方正方形DHFI.勾股定理由此得证.
刘徽的证法
返回
a
b
c
①
②
③
④
⑤
证法二 无字证明
青出
朱入
朱出
朱方
青方
青入
青入
青出
青出
证法三、青朱出入图
朱入
朱出
证法六、拼图游戏
又∵这两个正方形的边长都是a+b,所以面积相等,即
⑵
⑴
证明:图1的大正方形的面积为:
图2的大正方形的面积为:
