2021-2022学年苏科版八年级数学上册2.4线段、角的轴对称性 提升训练(word解析版)
文档属性
| 名称 | 2021-2022学年苏科版八年级数学上册2.4线段、角的轴对称性 提升训练(word解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 316.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-23 10:42:54 | ||
图片预览



文档简介
2021-2022学年苏科版八年级数学上册《2.4线段、角的轴对称性》
能力达标专题提升训练(附答案)
一、选择题
1.如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=8,则点P到BC的距离是( )
A.8
B.6
C.4
D.2
2.如图,△ABC的三边AB,BC,CA长分别是20,30,40,其三条角平分线将△ABC分为三个三角形,则S△ABO:S△BCO:S△CAO等于( )
A.1:1:1
B.1:2:3
C.2:3:4
D.3:4:5
3.如图,△ABC中,∠ABC、∠EAC的角平分线PA、PB交于点P,下列结论:
①PC平分∠ACF;
②∠ABC+∠APC=180°;
③若点M、N分别为点P在BE、BF上的正投影,则AM+CN=AC;
④∠BAC=2∠BPC.
其中正确的是( )
A.只有①②③
B.只有①③④
C.只有②③④
D.只有①③
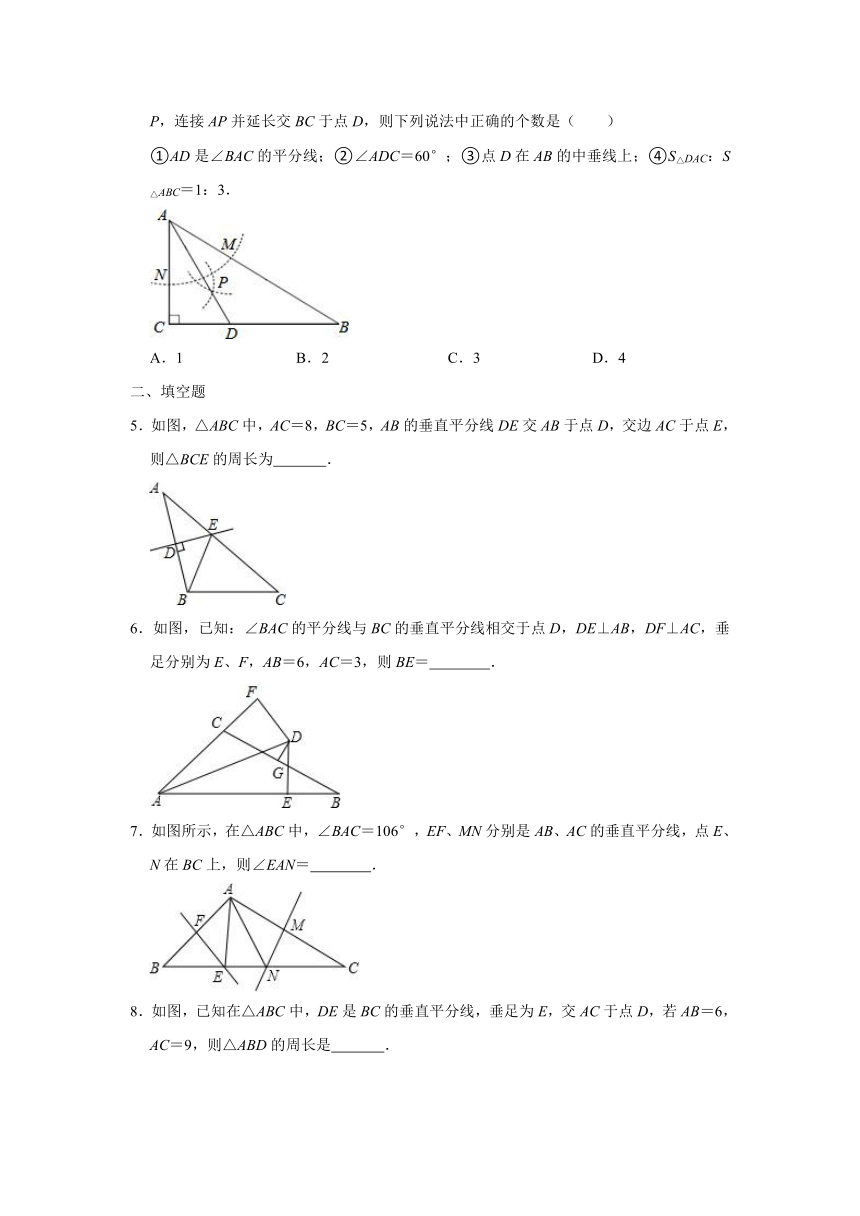
4.如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法中正确的个数是( )
①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的中垂线上;④S△DAC:S△ABC=1:3.
A.1
B.2
C.3
D.4
二、填空题
5.如图,△ABC中,AC=8,BC=5,AB的垂直平分线DE交AB于点D,交边AC于点E,则△BCE的周长为
.
6.如图,已知:∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,AB=6,AC=3,则BE=
.
7.如图所示,在△ABC中,∠BAC=106°,EF、MN分别是AB、AC的垂直平分线,点E、N在BC上,则∠EAN=
.
8.如图,已知在△ABC中,DE是BC的垂直平分线,垂足为E,交AC于点D,若AB=6,AC=9,则△ABD的周长是
.
9.如图,Rt△ABC中,∠B=90°,AB=4,BC=3,AC的垂直平分线DE分别交AB,AC于D,E两点,则CD的长为
.
10.如图:△ABC中,DE是AC的垂直平分线,AE=3cm,△ABD的周长为13cm,则△ABC的周长为
.
11.如图,在?ABCD中,AB=3,BC=5,对角线AC、BD相交于点O,过点O作OE⊥AC,交AD于点E,连接CE,则△CDE的周长为
.
12.已知:△ABC是三边都不相等的三角形,点P是三个内角平分线的交点,点O是三边垂直平分线的交点,当P、O同时在不等边△ABC的内部时,那么∠BOC和∠BPC的数量关系是:∠BOC=
.
13.如图,AD是∠BAC的平分线,EF垂直平分AD交BC的延长线于点F,若∠FAC=65°,则∠B的度数为
.
14.如图,在Rt△ABC中,∠B=90°,∠A=40°,AC的垂直平分线MN与AB交于点D,则∠BCD的度数是
度.
15.如图,在四边形ABCD中,∠A=90°,AD=4,连接BD,BD⊥CD,∠ADB=∠C.若P是BC边上一动点,则DP长的最小值为
.
16.如图,已知∠AOB=30°,P是∠AOB平分线上一点,CP∥OB,交OA于点C,PD⊥OB,垂足为点D,且PC=4,则PD等于
.
17.在四边形ABCD中,∠ADC与∠BCD的角平分线交于点E,∠DEC=115°,过点B作BF∥AD交CE于点F,CE=2BF,∠CBF=∠BCE,连接BE,S△BCE=4,则CE=
.
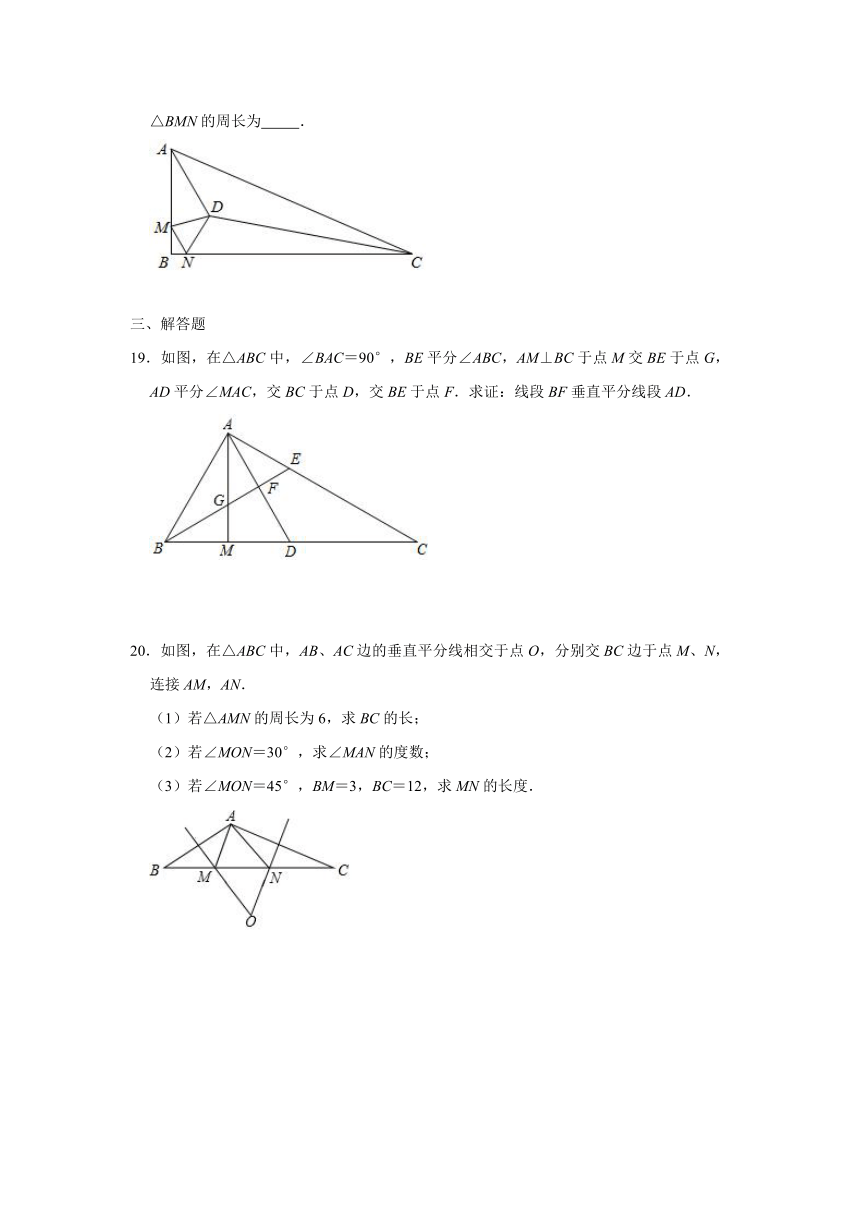
18.如图,在Rt△ABC中,∠ABC=90°.AB=5,AC=13,BC=12,∠BAC与∠ACB的角平分线相交于点D,点M、N分别在边AB、BC上,且∠MDN=45°,连接MN,则△BMN的周长为
.
三、解答题
19.如图,在△ABC中,∠BAC=90°,BE平分∠ABC,AM⊥BC于点M交BE于点G,AD平分∠MAC,交BC于点D,交BE于点F.求证:线段BF垂直平分线段AD.
20.如图,在△ABC中,AB、AC边的垂直平分线相交于点O,分别交BC边于点M、N,连接AM,AN.
(1)若△AMN的周长为6,求BC的长;
(2)若∠MON=30°,求∠MAN的度数;
(3)若∠MON=45°,BM=3,BC=12,求MN的长度.
21.如图,在四边形ABCD中,M,N分别是CD,BC的中点,且AM⊥CD,AN⊥BC.
(1)求证:∠BAD=2∠MAN;
(2)连接BD,若∠MAN=70°,∠DBC=40°,求∠ADC.
22.如图,在△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,点F在AC上,BE=FC.求证:BD=DF.
23.如图,△ABC的外角∠DAC的平分线交BC边的垂直平分线于P点,PD⊥AB于D,PE⊥AC于E.
(1)求证:BD=CE;
(2)若AB=6cm,AC=10cm,求AD的长.
参考答案
1.解:过点P作PE⊥BC于E,
∵AB∥CD,PA⊥AB,
∴PD⊥CD,
∵BP和CP分别平分∠ABC和∠DCB,
∴PA=PE,PD=PE,
∴PE=PA=PD,
∵PA+PD=AD=8,
∴PA=PD=4,
∴PE=4.
故选:C.
2.解:过点O作OD⊥AC于D,OE⊥AB于E,OF⊥BC于F,
∵点O是内心,
∴OE=OF=OD,
∴S△ABO:S△BCO:S△CAO=?AB?OE:?BC?OF:?AC?OD=AB:BC:AC=2:3:4,
故选:C.
3.解:如图,过点P作PM⊥AB,PN⊥BC,PD⊥AC,垂足分别为M、N、D,
①∵PB平分∠ABC,PA平分∠EAC,
∴PM=PN,PM=PD,
∴PM=PN=PD,
∴点P在∠ACF的角平分线上(到角的两边距离相等的点在角的平分线上),
故本小题正确;
②∵PM⊥AB,PN⊥BC,
∴∠ABC+90°+∠MPN+90°=360°,
∴∠ABC+∠MPN=180°,
很明显∠MPN≠∠APC,
∴∠ABC+∠APC=180°错误,
故本小题错误;
③在Rt△APM与Rt△APD中,,
∴Rt△APM≌Rt△APD(HL),
∴AD=AM,
同理可得Rt△CPD≌Rt△CPN,
∴CD=CN,
∴AM+CN=AD+CD=AC,
故本小题正确;
④∵PB平分∠ABC,PC平分∠ACF,
∴∠ACF=∠ABC+∠BAC,∠PCN=∠ACF=∠BPC+∠ABC,
∴∠BAC=2∠BPC,
故本小题正确.
综上所述,①③④正确.
故选:B.
4.解:①根据作图的过程可知,AD是∠BAC的平分线.
故①正确;
②如图,∵在△ABC中,∠C=90°,∠B=30°,
∴∠CAB=60°.
又∵AD是∠BAC的平分线,
∴∠1=∠2=∠CAB=30°,
∴∠3=90°﹣∠2=60°,即∠ADC=60°.
故②正确;
③∵∠1=∠B=30°,
∴AD=BD,
∴点D在AB的中垂线上.
故③正确;
④∵如图,在直角△ACD中,∠2=30°,
∴CD=AD,
∴BC=CD+BD=AD+AD=AD,S△DAC=AC?CD=AC?AD.
∴S△ABC=AC?BC=AC?AD=AC?AD,
∴S△DAC:S△ABC=AC?AD:AC?AD=1:3.
故④正确.
综上所述,正确的结论是:①②③④,共有4个.
故选:D.
5.解:∵DE是AB的垂直平分线,
∴EA=EB,
则△BCE的周长=BC+EC+EB=BC+EC+EA=BC+AC=13,
故答案为:13.
6.解:连接CD,BD,
∵AD是∠BAC的平分线,DE⊥AB,DF⊥AC,
∴DF=DE,∠F=∠DEB=90°,∠ADF=∠ADE,
∴AE=AF,
∵DG是BC的垂直平分线,
∴CD=BD,
在Rt△CDF和Rt△BDE中,
,
∴Rt△CDF≌Rt△BDE(HL),
∴BE=CF,
∴AB=AE+BE=AF+BE=AC+CF+BE=AC+2BE,
∵AB=6,AC=3,
∴BE=1.5.
故答案为:1.5.
7.解:∵△ABC中,∠BAC=106°,
∴∠B+∠C=180°﹣∠BAC=180°﹣106°=74°,
∵EF、MN分别是AB、AC的中垂线,
∴∠B=∠BAE,∠C=∠CAN,
即∠B+∠C=∠BAE+∠CAN=74°,
∴∠EAN=∠BAC﹣(∠BAE+∠CAN)=106°﹣74°=32°.
故答案为32°.
8.解:∵DE是BC的垂直平分线,
∴DB=DC,
∴△ABD的周长=AB+AD+BD=AB+AD+DC=AB+AC=15,
故答案为:15.
9.解:∵DE是AC的垂直平分线,
∴CD=AD,
∴AB=BD+AD=BD+CD,
设CD=x,则BD=4﹣x,
在Rt△BCD中,
CD2=BC2+BD2,即x2=32+(4﹣x)2,
解得x=.
故答案为:.
10.解:∵DE是AC的垂直平分线,
∴AD=CD,AC=2AE=6cm,
又∵△ABD的周长=AB+BD+AD=13cm,
∴AB+BD+CD=13cm,
即AB+BC=13cm,
∴△ABC的周长=AB+BC+AC=13+6=19cm.
故答案为19cm.
11.解:根据平行四边形的性质,
∴AO=OC,
∵OE⊥AC,
∴OE为AC的垂直平分线,
∴AE=EC,
∴△CDE的周长为:CD+AD=5+3=8,
故答案为:8.
12.解:∵BP平分∠ABC,CP平分∠ACB,
∴∠PBC=∠ABC,∠PCB=∠ACB,
∴∠BPC=180°﹣(∠PBC+∠PCB)
=180°﹣(
∠ABC+∠ACB)
=180°﹣(∠ABC+∠ACB)
=180°﹣(180°﹣∠BAC)
=90°+∠BAC,
即∠BAC=2∠BPC﹣180°;
如图,连接AO.
∵点O是这个三角形三边垂直平分线的交点,
∴OA=OB=OC,
∴∠OAB=∠OBA,∠OAC=∠OCA,∠OBC=∠OCB,
∴∠AOB=180°﹣2∠OAB,∠AOC=180°﹣2∠OAC,
∴∠BOC=360°﹣(∠AOB+∠AOC)
=360°﹣(180°﹣2∠OAB+180°﹣2∠OAC),
=2∠OAB+2∠OAC
=2∠BAC
=2(2∠BPC﹣180°)
=4∠BPC﹣360°,
故答案为:4∠BPC﹣360°.
13.解:∵AD平分∠CAB,
∴∠CAD=∠BAD,
设∠CAD=∠BAD=x°,
∵EF垂直平分AD,
∴FA=FD,
∴∠FDA=∠FAD,
∵∠FAC=65°,
∴∠FAD=∠FAC+∠CAD=65°+x°,
∵∠FDA=∠B+∠BAD=∠B+x°,
∴65°+x°=∠B+x°,
∴∠B=65°,
故答案为:65°.
14.解:∵Rt△ABC中,∠B=90°,∠A=40°,
∴∠BCN=180°﹣∠B﹣∠A=180°﹣90°﹣40°=50°,
∵DN是AC的垂直平分线,
∴DA=DC,∠A=∠DCA=40°,∠BCD=∠BCN﹣∠DCA=50°﹣40°=10°,
∠BCD的度数是10度.
故答案为:10.
15.解:根据垂线段最短,当DP⊥BC的时候,DP的长度最小,
∵BD⊥CD,即∠BDC=90°,又∠A=90°,
∴∠A=∠BDC,又∠ADB=∠C,
∴∠ABD=∠CBD,又DA⊥BA,DP⊥BC,
∴AD=DP,又AD=4,
∴DP=4.
故答案为:4.
16.解:作PE⊥OA于E,
∵CP∥OB,
∴∠OPC=∠POD,
∵P是∠AOB平分线上一点,
∴∠POA=∠POD=15°,
∴∠ACP=∠OPC+∠POA=30°,
∴PE=PC=2,
∵P是∠AOB平分线上一点,PD⊥OB,PE⊥OA,
∴PD=PE=2,
故答案为:2.
17.解:∵∠CBF=∠BCE,
∴可以假设∠BCE=4x,则∠CBF=5x,
∵DE平分∠ADC,CE平分∠DCB,
∴∠ADE=∠EDC,∠ECD=∠ECB=4x,设∠ADE=∠EDC=y,
∵AD∥BF,
∴∠A+∠ABF=180°,
∴∠ADC+∠DCB+∠CBF=180°,
∴2y+13x=180°①,
∵∠DEC=115°,
∴∠EDC+∠ECD=65°,即y+4x=65°
②,
由①②解得,
∴∠BCF=40°,∠CBF=50°,
∴∠CFB=90°,
∴BF⊥EC,
∴CE=2BF,设BF=m,则CE=2m,
∵S△BCE=?EC?BF=4,
∴×2m×m=4,
∴m=2或﹣2(舍弃),
∴CE=2m=4,
故答案为4.
18.解:过D点作DE⊥AB于E,DF⊥BC于F,DH⊥AC于H,如图,
∵DA平分∠BAC,
∴DE=DH,
同理可得DF=DH,
∴DE=DF,
∵∠DEB=∠B=∠DFB=90°,
∴四边形BEDF为正方形,
∴BE=BF=DE=DF,
在Rt△ADE和Rt△ADH中
,
∴Rt△ADE≌Rt△ADH(HL),
∴AE=AH,
同理可得Rt△CDF≌Rt△CDH(HL),
∴CF=CH,
设正方形BEDF的边长为x,则AE=AH=5﹣x,CF=CH=12﹣x,
∵AH+CH=AC,
∴5﹣x+12﹣x=13,解得x=2,
即BE=2,
在FC上截取FP=EM,如图,
∵DE=DF,∠DEM=∠DFP,EM=FP,
∴△DEM≌△DFP(SAS),
∴DM=DP,∠EDM=∠FDP,
∴∠MDP=∠EDF=90°,
∵∠MDN=45°,
∴∠PDN=45°,
在△DMN和△DPN中,
,
∴△DMN≌△DPN(SAS),
∴MN=NP=NF+FP=NF+EM,
∴△BMN的周长=MN+BM+BN=EM+BM+BN+NF=BE+BF=2+2=4.
故答案为4.
19.证明:∵∠BAC=90°,
∴∠ABC+∠C=90°,
∵AM⊥BC,
∴∠AMB=90°,
∴∠ABC+∠BAM=90°,
∴∠C=∠BAM,
∵AD平分∠MAC,
∴∠MAD=∠CAD,
∴∠BAM+∠MAD=∠C+∠CAD,
∵∠ADB=∠C+∠CAD,
∴∠BAD=∠ADB,
∴AB=BD,
∵BE平分∠ABC,
∴BF⊥AD,AF=FD,
即线段BF垂直平分线段AD.
20.解:(1)∵直线OM是AB的垂直平分线,
∴MA=MB,
同理,NA=NC,
∵△AMN的周长为6,
∴MA+MN+NA=6,即MB+MN+NC=BC=6;
(2)∵∠MON=30°,
∴∠OMN+∠ONM=150°,
∴∠BME+∠CNF=150°,
∵MA=MB,ME⊥AB,
∴∠BMA=2∠BME,
同理,∠ANC=2∠CNF,
∴∠BMA+∠ANC=300°,
∴∠AMN+∠ANM=360°﹣300°=60°,
∴∠MAN=180°﹣60°=120°;
(3)由(2)的作法可知,∠MAN=90°,
由(1)可知,MA=MB=3,NA=NC
设MN=x,
∴NA=NC=12﹣3﹣x=9﹣x,
由勾股定理得,MN2=AM2+AN2,即x2=32+(9﹣x)2,
解得,x=5,即MN=5.
21.(1)证明:连接AC,
∵M是CD的中点,AM⊥CD,
∴AM是线段CD的垂直平分线,
∴AC=AD,又AM⊥CD,
∴∠3=∠4,
同理,∠1=∠2,
∴∠2+∠3=∠BAD,即∠BAD=2∠MAN;
(2)∵AM⊥CD,AN⊥BC.∠MAN=70°,
∴∠BCD=360°﹣90°﹣90°﹣70°=110°,
∴∠BDC=180°﹣∠DBC﹣∠BCD=30°,
∠BAD=2∠MAN=140°,
∵AB=AC,AD=AC,
∴AB=AD,
∴∠ADB=∠ABD=20°,
∴∠ADC=∠ADB+∠BDC=50°.
22.证明:∵AD平分∠BAC,DE⊥AB,∠C=90°,
∴DC=DE,
在△DCF和△DEB中,,
∴△DCF≌△DEB,(SAS),
∴BD=DF.
23.(1)证明:连接BP、CP,
∵点P在BC的垂直平分线上,
∴BP=CP,
∵AP是∠DAC的平分线,
∴DP=EP,
在Rt△BDP和Rt△CEP中,,
∴Rt△BDP≌Rt△CEP(HL),
∴BD=CE;
(2)解:在Rt△ADP和Rt△AEP中,,
∴Rt△ADP≌Rt△AEP(HL),
∴AD=AE,
∵AB=6cm,AC=10cm,
∴6+AD=10﹣AE,
即6+AD=10﹣AD,
解得AD=2cm.
能力达标专题提升训练(附答案)
一、选择题
1.如图,AB∥CD,BP和CP分别平分∠ABC和∠DCB,AD过点P,且与AB垂直.若AD=8,则点P到BC的距离是( )
A.8
B.6
C.4
D.2
2.如图,△ABC的三边AB,BC,CA长分别是20,30,40,其三条角平分线将△ABC分为三个三角形,则S△ABO:S△BCO:S△CAO等于( )
A.1:1:1
B.1:2:3
C.2:3:4
D.3:4:5
3.如图,△ABC中,∠ABC、∠EAC的角平分线PA、PB交于点P,下列结论:
①PC平分∠ACF;
②∠ABC+∠APC=180°;
③若点M、N分别为点P在BE、BF上的正投影,则AM+CN=AC;
④∠BAC=2∠BPC.
其中正确的是( )
A.只有①②③
B.只有①③④
C.只有②③④
D.只有①③
4.如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法中正确的个数是( )
①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的中垂线上;④S△DAC:S△ABC=1:3.
A.1
B.2
C.3
D.4
二、填空题
5.如图,△ABC中,AC=8,BC=5,AB的垂直平分线DE交AB于点D,交边AC于点E,则△BCE的周长为
.
6.如图,已知:∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E、F,AB=6,AC=3,则BE=
.
7.如图所示,在△ABC中,∠BAC=106°,EF、MN分别是AB、AC的垂直平分线,点E、N在BC上,则∠EAN=
.
8.如图,已知在△ABC中,DE是BC的垂直平分线,垂足为E,交AC于点D,若AB=6,AC=9,则△ABD的周长是
.
9.如图,Rt△ABC中,∠B=90°,AB=4,BC=3,AC的垂直平分线DE分别交AB,AC于D,E两点,则CD的长为
.
10.如图:△ABC中,DE是AC的垂直平分线,AE=3cm,△ABD的周长为13cm,则△ABC的周长为
.
11.如图,在?ABCD中,AB=3,BC=5,对角线AC、BD相交于点O,过点O作OE⊥AC,交AD于点E,连接CE,则△CDE的周长为
.
12.已知:△ABC是三边都不相等的三角形,点P是三个内角平分线的交点,点O是三边垂直平分线的交点,当P、O同时在不等边△ABC的内部时,那么∠BOC和∠BPC的数量关系是:∠BOC=
.
13.如图,AD是∠BAC的平分线,EF垂直平分AD交BC的延长线于点F,若∠FAC=65°,则∠B的度数为
.
14.如图,在Rt△ABC中,∠B=90°,∠A=40°,AC的垂直平分线MN与AB交于点D,则∠BCD的度数是
度.
15.如图,在四边形ABCD中,∠A=90°,AD=4,连接BD,BD⊥CD,∠ADB=∠C.若P是BC边上一动点,则DP长的最小值为
.
16.如图,已知∠AOB=30°,P是∠AOB平分线上一点,CP∥OB,交OA于点C,PD⊥OB,垂足为点D,且PC=4,则PD等于
.
17.在四边形ABCD中,∠ADC与∠BCD的角平分线交于点E,∠DEC=115°,过点B作BF∥AD交CE于点F,CE=2BF,∠CBF=∠BCE,连接BE,S△BCE=4,则CE=
.
18.如图,在Rt△ABC中,∠ABC=90°.AB=5,AC=13,BC=12,∠BAC与∠ACB的角平分线相交于点D,点M、N分别在边AB、BC上,且∠MDN=45°,连接MN,则△BMN的周长为
.
三、解答题
19.如图,在△ABC中,∠BAC=90°,BE平分∠ABC,AM⊥BC于点M交BE于点G,AD平分∠MAC,交BC于点D,交BE于点F.求证:线段BF垂直平分线段AD.
20.如图,在△ABC中,AB、AC边的垂直平分线相交于点O,分别交BC边于点M、N,连接AM,AN.
(1)若△AMN的周长为6,求BC的长;
(2)若∠MON=30°,求∠MAN的度数;
(3)若∠MON=45°,BM=3,BC=12,求MN的长度.
21.如图,在四边形ABCD中,M,N分别是CD,BC的中点,且AM⊥CD,AN⊥BC.
(1)求证:∠BAD=2∠MAN;
(2)连接BD,若∠MAN=70°,∠DBC=40°,求∠ADC.
22.如图,在△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,点F在AC上,BE=FC.求证:BD=DF.
23.如图,△ABC的外角∠DAC的平分线交BC边的垂直平分线于P点,PD⊥AB于D,PE⊥AC于E.
(1)求证:BD=CE;
(2)若AB=6cm,AC=10cm,求AD的长.
参考答案
1.解:过点P作PE⊥BC于E,
∵AB∥CD,PA⊥AB,
∴PD⊥CD,
∵BP和CP分别平分∠ABC和∠DCB,
∴PA=PE,PD=PE,
∴PE=PA=PD,
∵PA+PD=AD=8,
∴PA=PD=4,
∴PE=4.
故选:C.
2.解:过点O作OD⊥AC于D,OE⊥AB于E,OF⊥BC于F,
∵点O是内心,
∴OE=OF=OD,
∴S△ABO:S△BCO:S△CAO=?AB?OE:?BC?OF:?AC?OD=AB:BC:AC=2:3:4,
故选:C.
3.解:如图,过点P作PM⊥AB,PN⊥BC,PD⊥AC,垂足分别为M、N、D,
①∵PB平分∠ABC,PA平分∠EAC,
∴PM=PN,PM=PD,
∴PM=PN=PD,
∴点P在∠ACF的角平分线上(到角的两边距离相等的点在角的平分线上),
故本小题正确;
②∵PM⊥AB,PN⊥BC,
∴∠ABC+90°+∠MPN+90°=360°,
∴∠ABC+∠MPN=180°,
很明显∠MPN≠∠APC,
∴∠ABC+∠APC=180°错误,
故本小题错误;
③在Rt△APM与Rt△APD中,,
∴Rt△APM≌Rt△APD(HL),
∴AD=AM,
同理可得Rt△CPD≌Rt△CPN,
∴CD=CN,
∴AM+CN=AD+CD=AC,
故本小题正确;
④∵PB平分∠ABC,PC平分∠ACF,
∴∠ACF=∠ABC+∠BAC,∠PCN=∠ACF=∠BPC+∠ABC,
∴∠BAC=2∠BPC,
故本小题正确.
综上所述,①③④正确.
故选:B.
4.解:①根据作图的过程可知,AD是∠BAC的平分线.
故①正确;
②如图,∵在△ABC中,∠C=90°,∠B=30°,
∴∠CAB=60°.
又∵AD是∠BAC的平分线,
∴∠1=∠2=∠CAB=30°,
∴∠3=90°﹣∠2=60°,即∠ADC=60°.
故②正确;
③∵∠1=∠B=30°,
∴AD=BD,
∴点D在AB的中垂线上.
故③正确;
④∵如图,在直角△ACD中,∠2=30°,
∴CD=AD,
∴BC=CD+BD=AD+AD=AD,S△DAC=AC?CD=AC?AD.
∴S△ABC=AC?BC=AC?AD=AC?AD,
∴S△DAC:S△ABC=AC?AD:AC?AD=1:3.
故④正确.
综上所述,正确的结论是:①②③④,共有4个.
故选:D.
5.解:∵DE是AB的垂直平分线,
∴EA=EB,
则△BCE的周长=BC+EC+EB=BC+EC+EA=BC+AC=13,
故答案为:13.
6.解:连接CD,BD,
∵AD是∠BAC的平分线,DE⊥AB,DF⊥AC,
∴DF=DE,∠F=∠DEB=90°,∠ADF=∠ADE,
∴AE=AF,
∵DG是BC的垂直平分线,
∴CD=BD,
在Rt△CDF和Rt△BDE中,
,
∴Rt△CDF≌Rt△BDE(HL),
∴BE=CF,
∴AB=AE+BE=AF+BE=AC+CF+BE=AC+2BE,
∵AB=6,AC=3,
∴BE=1.5.
故答案为:1.5.
7.解:∵△ABC中,∠BAC=106°,
∴∠B+∠C=180°﹣∠BAC=180°﹣106°=74°,
∵EF、MN分别是AB、AC的中垂线,
∴∠B=∠BAE,∠C=∠CAN,
即∠B+∠C=∠BAE+∠CAN=74°,
∴∠EAN=∠BAC﹣(∠BAE+∠CAN)=106°﹣74°=32°.
故答案为32°.
8.解:∵DE是BC的垂直平分线,
∴DB=DC,
∴△ABD的周长=AB+AD+BD=AB+AD+DC=AB+AC=15,
故答案为:15.
9.解:∵DE是AC的垂直平分线,
∴CD=AD,
∴AB=BD+AD=BD+CD,
设CD=x,则BD=4﹣x,
在Rt△BCD中,
CD2=BC2+BD2,即x2=32+(4﹣x)2,
解得x=.
故答案为:.
10.解:∵DE是AC的垂直平分线,
∴AD=CD,AC=2AE=6cm,
又∵△ABD的周长=AB+BD+AD=13cm,
∴AB+BD+CD=13cm,
即AB+BC=13cm,
∴△ABC的周长=AB+BC+AC=13+6=19cm.
故答案为19cm.
11.解:根据平行四边形的性质,
∴AO=OC,
∵OE⊥AC,
∴OE为AC的垂直平分线,
∴AE=EC,
∴△CDE的周长为:CD+AD=5+3=8,
故答案为:8.
12.解:∵BP平分∠ABC,CP平分∠ACB,
∴∠PBC=∠ABC,∠PCB=∠ACB,
∴∠BPC=180°﹣(∠PBC+∠PCB)
=180°﹣(
∠ABC+∠ACB)
=180°﹣(∠ABC+∠ACB)
=180°﹣(180°﹣∠BAC)
=90°+∠BAC,
即∠BAC=2∠BPC﹣180°;
如图,连接AO.
∵点O是这个三角形三边垂直平分线的交点,
∴OA=OB=OC,
∴∠OAB=∠OBA,∠OAC=∠OCA,∠OBC=∠OCB,
∴∠AOB=180°﹣2∠OAB,∠AOC=180°﹣2∠OAC,
∴∠BOC=360°﹣(∠AOB+∠AOC)
=360°﹣(180°﹣2∠OAB+180°﹣2∠OAC),
=2∠OAB+2∠OAC
=2∠BAC
=2(2∠BPC﹣180°)
=4∠BPC﹣360°,
故答案为:4∠BPC﹣360°.
13.解:∵AD平分∠CAB,
∴∠CAD=∠BAD,
设∠CAD=∠BAD=x°,
∵EF垂直平分AD,
∴FA=FD,
∴∠FDA=∠FAD,
∵∠FAC=65°,
∴∠FAD=∠FAC+∠CAD=65°+x°,
∵∠FDA=∠B+∠BAD=∠B+x°,
∴65°+x°=∠B+x°,
∴∠B=65°,
故答案为:65°.
14.解:∵Rt△ABC中,∠B=90°,∠A=40°,
∴∠BCN=180°﹣∠B﹣∠A=180°﹣90°﹣40°=50°,
∵DN是AC的垂直平分线,
∴DA=DC,∠A=∠DCA=40°,∠BCD=∠BCN﹣∠DCA=50°﹣40°=10°,
∠BCD的度数是10度.
故答案为:10.
15.解:根据垂线段最短,当DP⊥BC的时候,DP的长度最小,
∵BD⊥CD,即∠BDC=90°,又∠A=90°,
∴∠A=∠BDC,又∠ADB=∠C,
∴∠ABD=∠CBD,又DA⊥BA,DP⊥BC,
∴AD=DP,又AD=4,
∴DP=4.
故答案为:4.
16.解:作PE⊥OA于E,
∵CP∥OB,
∴∠OPC=∠POD,
∵P是∠AOB平分线上一点,
∴∠POA=∠POD=15°,
∴∠ACP=∠OPC+∠POA=30°,
∴PE=PC=2,
∵P是∠AOB平分线上一点,PD⊥OB,PE⊥OA,
∴PD=PE=2,
故答案为:2.
17.解:∵∠CBF=∠BCE,
∴可以假设∠BCE=4x,则∠CBF=5x,
∵DE平分∠ADC,CE平分∠DCB,
∴∠ADE=∠EDC,∠ECD=∠ECB=4x,设∠ADE=∠EDC=y,
∵AD∥BF,
∴∠A+∠ABF=180°,
∴∠ADC+∠DCB+∠CBF=180°,
∴2y+13x=180°①,
∵∠DEC=115°,
∴∠EDC+∠ECD=65°,即y+4x=65°
②,
由①②解得,
∴∠BCF=40°,∠CBF=50°,
∴∠CFB=90°,
∴BF⊥EC,
∴CE=2BF,设BF=m,则CE=2m,
∵S△BCE=?EC?BF=4,
∴×2m×m=4,
∴m=2或﹣2(舍弃),
∴CE=2m=4,
故答案为4.
18.解:过D点作DE⊥AB于E,DF⊥BC于F,DH⊥AC于H,如图,
∵DA平分∠BAC,
∴DE=DH,
同理可得DF=DH,
∴DE=DF,
∵∠DEB=∠B=∠DFB=90°,
∴四边形BEDF为正方形,
∴BE=BF=DE=DF,
在Rt△ADE和Rt△ADH中
,
∴Rt△ADE≌Rt△ADH(HL),
∴AE=AH,
同理可得Rt△CDF≌Rt△CDH(HL),
∴CF=CH,
设正方形BEDF的边长为x,则AE=AH=5﹣x,CF=CH=12﹣x,
∵AH+CH=AC,
∴5﹣x+12﹣x=13,解得x=2,
即BE=2,
在FC上截取FP=EM,如图,
∵DE=DF,∠DEM=∠DFP,EM=FP,
∴△DEM≌△DFP(SAS),
∴DM=DP,∠EDM=∠FDP,
∴∠MDP=∠EDF=90°,
∵∠MDN=45°,
∴∠PDN=45°,
在△DMN和△DPN中,
,
∴△DMN≌△DPN(SAS),
∴MN=NP=NF+FP=NF+EM,
∴△BMN的周长=MN+BM+BN=EM+BM+BN+NF=BE+BF=2+2=4.
故答案为4.
19.证明:∵∠BAC=90°,
∴∠ABC+∠C=90°,
∵AM⊥BC,
∴∠AMB=90°,
∴∠ABC+∠BAM=90°,
∴∠C=∠BAM,
∵AD平分∠MAC,
∴∠MAD=∠CAD,
∴∠BAM+∠MAD=∠C+∠CAD,
∵∠ADB=∠C+∠CAD,
∴∠BAD=∠ADB,
∴AB=BD,
∵BE平分∠ABC,
∴BF⊥AD,AF=FD,
即线段BF垂直平分线段AD.
20.解:(1)∵直线OM是AB的垂直平分线,
∴MA=MB,
同理,NA=NC,
∵△AMN的周长为6,
∴MA+MN+NA=6,即MB+MN+NC=BC=6;
(2)∵∠MON=30°,
∴∠OMN+∠ONM=150°,
∴∠BME+∠CNF=150°,
∵MA=MB,ME⊥AB,
∴∠BMA=2∠BME,
同理,∠ANC=2∠CNF,
∴∠BMA+∠ANC=300°,
∴∠AMN+∠ANM=360°﹣300°=60°,
∴∠MAN=180°﹣60°=120°;
(3)由(2)的作法可知,∠MAN=90°,
由(1)可知,MA=MB=3,NA=NC
设MN=x,
∴NA=NC=12﹣3﹣x=9﹣x,
由勾股定理得,MN2=AM2+AN2,即x2=32+(9﹣x)2,
解得,x=5,即MN=5.
21.(1)证明:连接AC,
∵M是CD的中点,AM⊥CD,
∴AM是线段CD的垂直平分线,
∴AC=AD,又AM⊥CD,
∴∠3=∠4,
同理,∠1=∠2,
∴∠2+∠3=∠BAD,即∠BAD=2∠MAN;
(2)∵AM⊥CD,AN⊥BC.∠MAN=70°,
∴∠BCD=360°﹣90°﹣90°﹣70°=110°,
∴∠BDC=180°﹣∠DBC﹣∠BCD=30°,
∠BAD=2∠MAN=140°,
∵AB=AC,AD=AC,
∴AB=AD,
∴∠ADB=∠ABD=20°,
∴∠ADC=∠ADB+∠BDC=50°.
22.证明:∵AD平分∠BAC,DE⊥AB,∠C=90°,
∴DC=DE,
在△DCF和△DEB中,,
∴△DCF≌△DEB,(SAS),
∴BD=DF.
23.(1)证明:连接BP、CP,
∵点P在BC的垂直平分线上,
∴BP=CP,
∵AP是∠DAC的平分线,
∴DP=EP,
在Rt△BDP和Rt△CEP中,,
∴Rt△BDP≌Rt△CEP(HL),
∴BD=CE;
(2)解:在Rt△ADP和Rt△AEP中,,
∴Rt△ADP≌Rt△AEP(HL),
∴AD=AE,
∵AB=6cm,AC=10cm,
∴6+AD=10﹣AE,
即6+AD=10﹣AD,
解得AD=2cm.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
