《2.6正多边形和圆》能力达标专题突破训练(Word版 附答案)2021-2022学年九年级数学苏科版上册
文档属性
| 名称 | 《2.6正多边形和圆》能力达标专题突破训练(Word版 附答案)2021-2022学年九年级数学苏科版上册 |  | |
| 格式 | doc | ||
| 文件大小 | 493.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-23 11:11:10 | ||
图片预览

文档简介
2021-2022苏科版九年级数学上册《2.6正多边形和圆》能力达标专题突破训练(附答案)
一、选择题
1.如图,正方形ABCD内接于⊙O.点E为上一点,连接BE、CE,若∠CBE=15°,BE=3,则BC的长为( )
A.
B.
C.
D.
2.如图,将边长相等的正方形、正五边形、正六边形纸板,按如图方式放在桌面上,则∠a的度数是( )
A.42°
B.40°
C.36°
D.32°
3.正多边形的内切圆与外接圆的半径之比为,则这个正多边形为( )
A.正十二边形
B.正六边形
C.正四边形
D.正三角形
4.如图,若⊙O是正方形ABCD与正六边形AEFCGH的外接圆,则正方形ABCD与正六边形AEFCGH的周长之比为( )
A.2:3
B.:1
C.:
D.1:
5.如图,正方形ABCD内接于⊙O,线段MN在对角线BD上运动,若⊙O的面积为2π,MN=1,则△AMN周长的最小值是( )
A.3
B.4
C.5
D.6
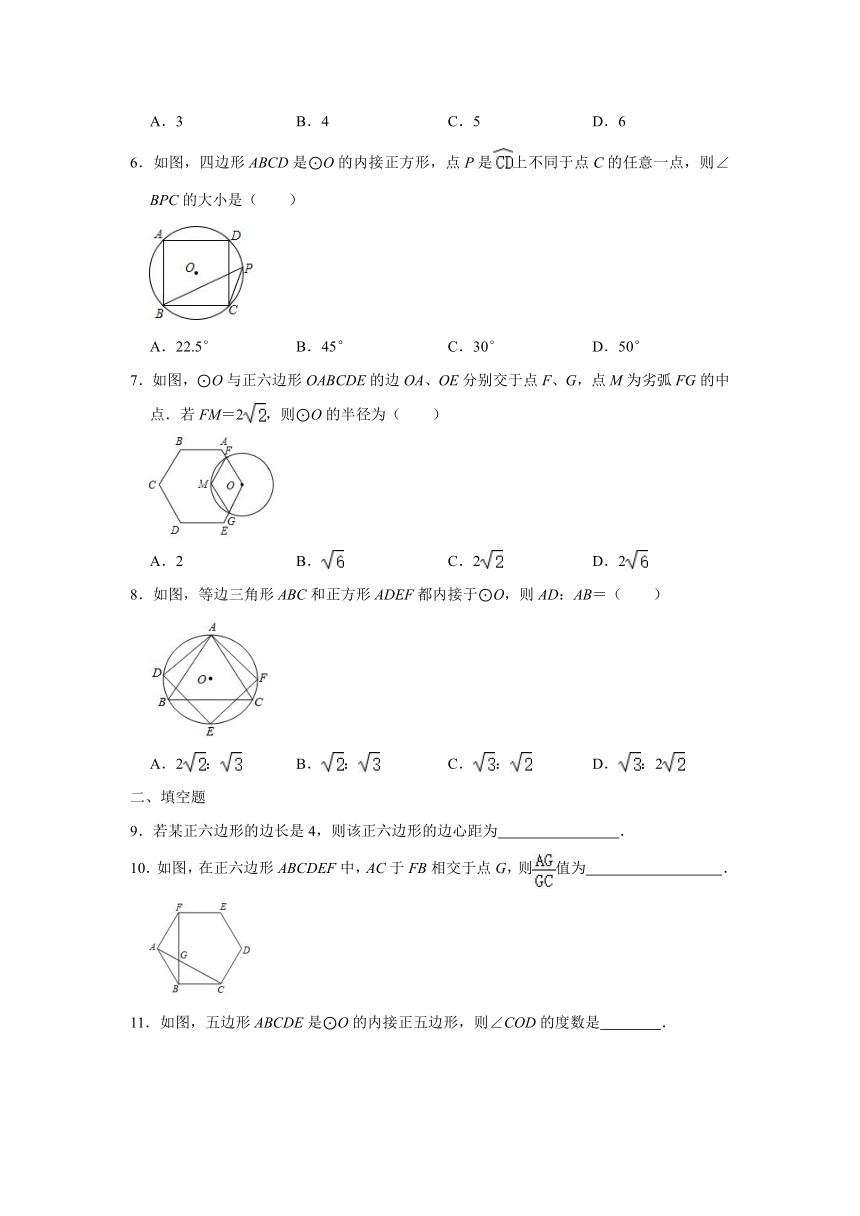
6.如图,四边形ABCD是⊙O的内接正方形,点P是上不同于点C的任意一点,则∠BPC的大小是( )
A.22.5°
B.45°
C.30°
D.50°
7.如图,⊙O与正六边形OABCDE的边OA、OE分别交于点F、G,点M为劣弧FG的中点.若FM=2,则⊙O的半径为( )
A.2
B.
C.2
D.2
8.如图,等边三角形ABC和正方形ADEF都内接于⊙O,则AD:AB=( )
A.2:
B.:
C.:
D.:2
二、填空题
9.若某正六边形的边长是4,则该正六边形的边心距为
.
10.如图,在正六边形ABCDEF中,AC于FB相交于点G,则值为
.
11.如图,五边形ABCDE是⊙O的内接正五边形,则∠COD的度数是
.
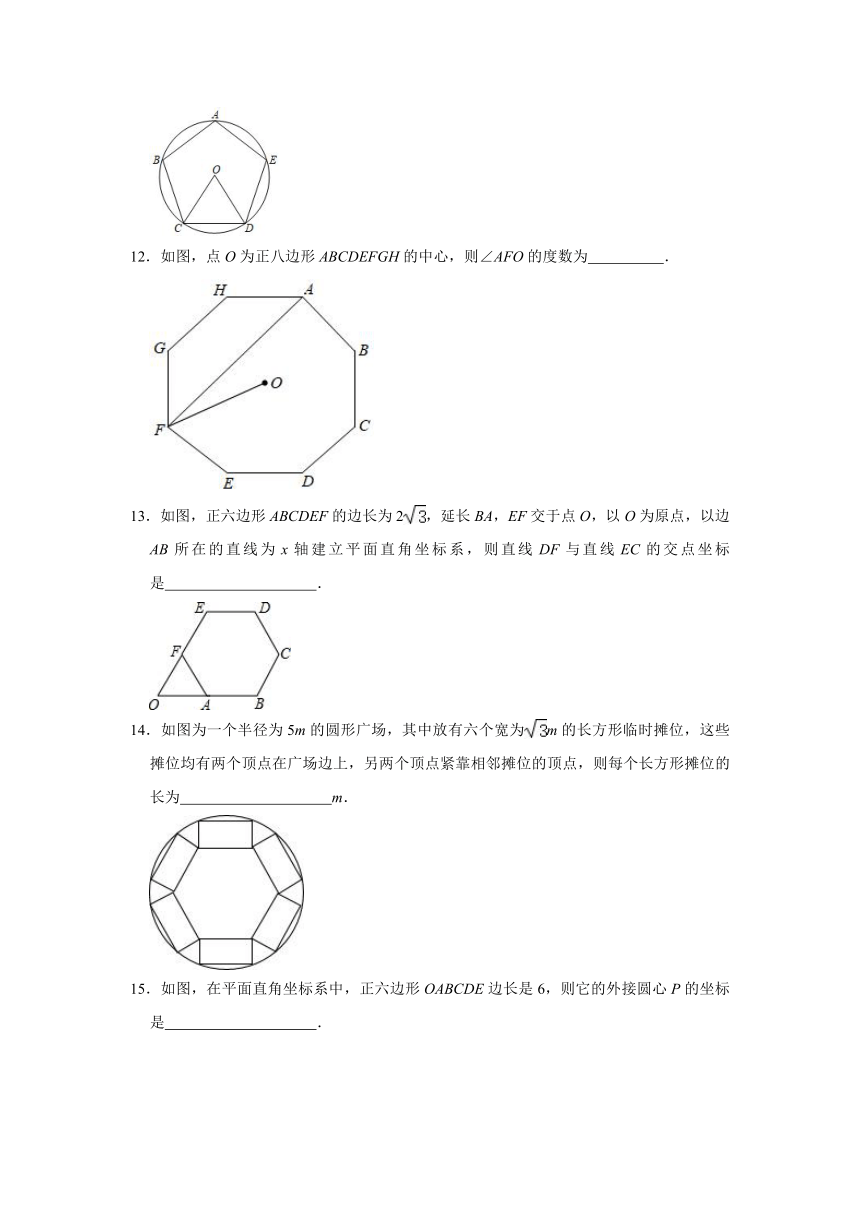
12.如图,点O为正八边形ABCDEFGH的中心,则∠AFO的度数为
.
13.如图,正六边形ABCDEF的边长为2,延长BA,EF交于点O,以O为原点,以边AB所在的直线为x轴建立平面直角坐标系,则直线DF与直线EC的交点坐标是
.
14.如图为一个半径为5m的圆形广场,其中放有六个宽为m的长方形临时摊位,这些摊位均有两个顶点在广场边上,另两个顶点紧靠相邻摊位的顶点,则每个长方形摊位的长为
m.
15.如图,在平面直角坐标系中,正六边形OABCDE边长是6,则它的外接圆心P的坐标是
.
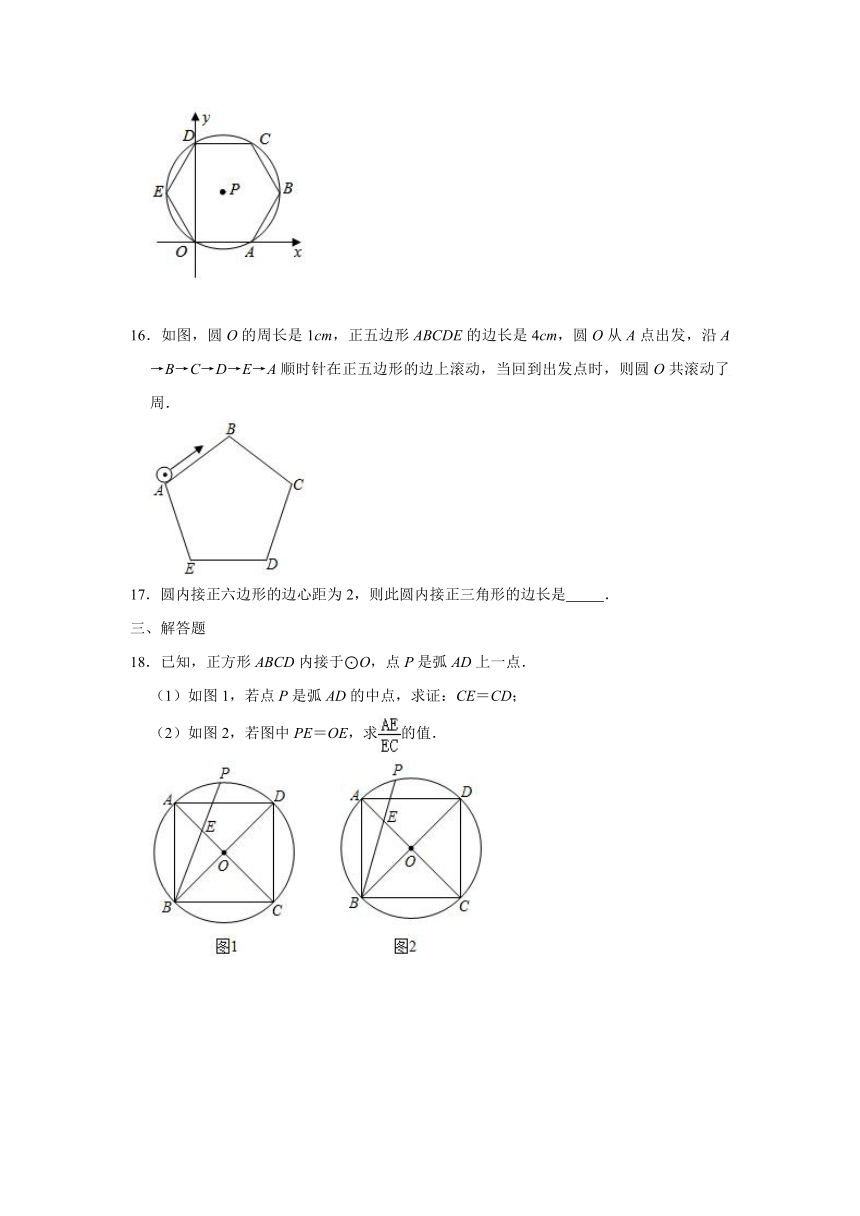
16.如图,圆O的周长是1cm,正五边形ABCDE的边长是4cm,圆O从A点出发,沿A→B→C→D→E→A顺时针在正五边形的边上滚动,当回到出发点时,则圆O共滚动了
周.
17.圆内接正六边形的边心距为2,则此圆内接正三角形的边长是
.
三、解答题
18.已知,正方形ABCD内接于⊙O,点P是弧AD上一点.
(1)如图1,若点P是弧AD的中点,求证:CE=CD;
(2)如图2,若图中PE=OE,求的值.
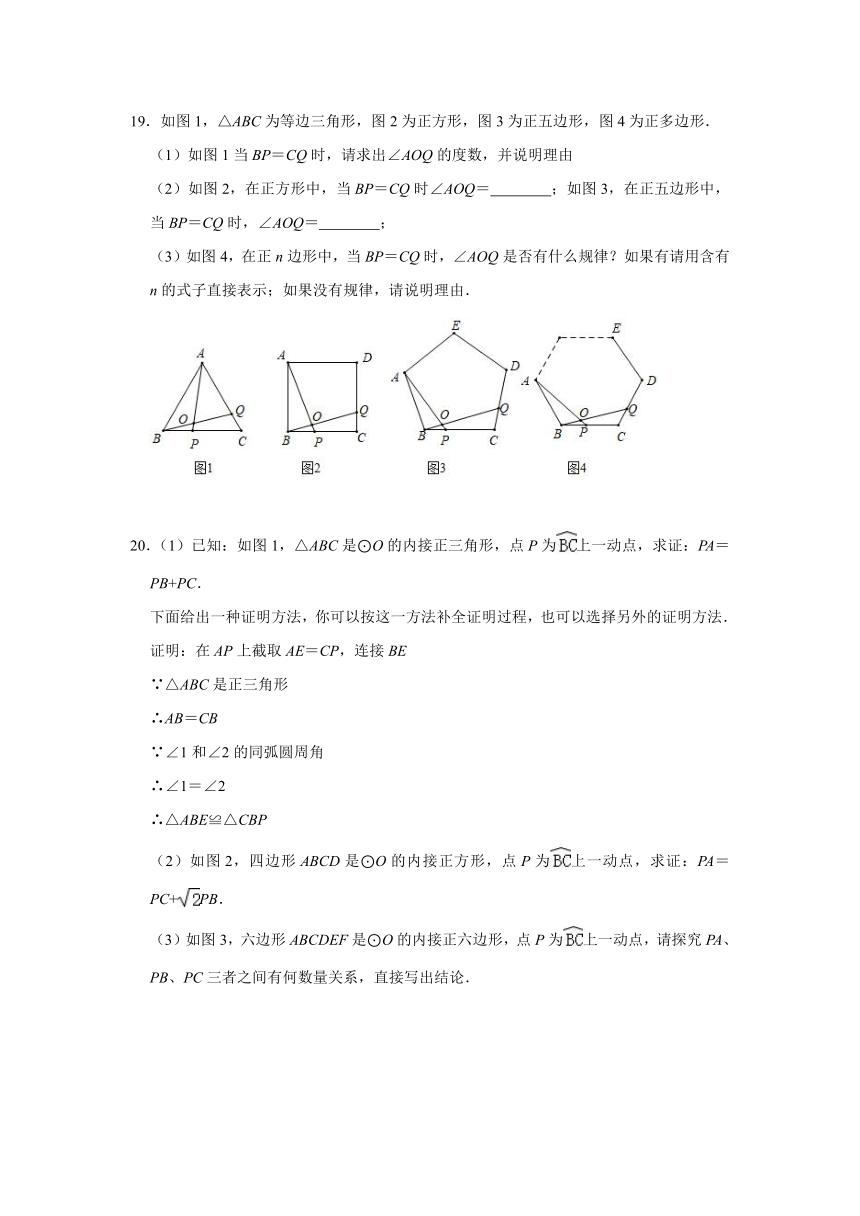
19.如图1,△ABC为等边三角形,图2为正方形,图3为正五边形,图4为正多边形.
(1)如图1当BP=CQ时,请求出∠AOQ的度数,并说明理由
(2)如图2,在正方形中,当BP=CQ时∠AOQ=
;如图3,在正五边形中,当BP=CQ时,∠AOQ=
;
(3)如图4,在正n边形中,当BP=CQ时,∠AOQ是否有什么规律?如果有请用含有n的式子直接表示;如果没有规律,请说明理由.
20.(1)已知:如图1,△ABC是⊙O的内接正三角形,点P为上一动点,求证:PA=PB+PC.
下面给出一种证明方法,你可以按这一方法补全证明过程,也可以选择另外的证明方法.
证明:在AP上截取AE=CP,连接BE
∵△ABC是正三角形
∴AB=CB
∵∠1和∠2的同弧圆周角
∴∠1=∠2
∴△ABE≌△CBP
(2)如图2,四边形ABCD是⊙O的内接正方形,点P为上一动点,求证:PA=PC+PB.
(3)如图3,六边形ABCDEF是⊙O的内接正六边形,点P为上一动点,请探究PA、PB、PC三者之间有何数量关系,直接写出结论.
21.如图,正六边形ABCDEF内接于⊙O,BE是⊙O的直径,连接BF,延长BA,过F作FG⊥BA,垂足为G.
(1)求证:FG是⊙O的切线;
(2)已知FG=2,求图中阴影部分的面积.
22.探究题:
(1)
都相等,
都相等的多边形叫做正多边形;
(2)如图,格点长方形MNPQ的各点分布在边长均为1的等边三角形组成的网格上,请在格点长方形MNPQ内画出一个面积最大的格点正六边形ABCDEF,并简要说明它是正六边形的理由;
(3)正六边形有
条对角线,它的外角和为
度.
参考答案
1.解:连接OA,OB,OE,
∵正方形ABCD内接于⊙O,
∴OA=OB=OE,∠AOB==90°,AB=BC,∠ABC=90°,
∴∠OAB=∠OBA=(180°﹣∠AOB)=45°,
∴∠OBC=∠ABC﹣∠OBA=45°,
∵∠CBE=15°,
∴∠OBE=∠OBC+∠CBE=60°,
∴△OBE是等边三角形,
∴OB=BE=3,
∴OA=3,
∴AB==3,
∴BC=3,
故选:D.
2.解:正方形的内角为90°,
正五边形的内角为=108°,
正六边形的内角为=120°,
∠1=360°﹣90°﹣108°﹣120°=42°,
故选:A.
3.解:如图,设AB是正多边形的一边,O为正多边形的内切圆与外接圆的圆心,OC⊥AB于C,
∵正多边形的内切圆与外接圆的半径之比为,
∴=,
在Rt△AOC中,cos∠AOC==,
∴∠AOC=45°,
∴∠AOB=2∠AOC=90°,
则正多边形边数为:=4.
故选:C.
4.解:连接OA、OB.OE,如图所示:
设此圆的半径为R,
则它的内接正方形的边长为R,它的内接正六边形的边长为R,
∴内接正方形和内接正六边形的边长之比为R:R=:1,
∴正方形ABCD与正六边形AEFCGH的周长之比=内接正方形和内接正六边形的边长之比=4:6=2:3,
故选:A.
5.解:⊙O的面积为2π,则圆的半径为,则BD=2=AC,
由正方形的性质,知点C是点A关于BD的对称点,
过点C作CA′∥BD,且使CA′=1,
连接AA′交BD于点N,取NM=1,连接AM、CM,则点M、N为所求点,
理由:∵A′C∥MN,且A′C=MN,则四边形MCA′N为平行四边形,
则A′N=CM=AM,
故△AMN的周长=AM+AN+MN=AA′+1为最小,
则A′A==3,
则△AMN的周长的最小值为3+1=4,
故选:B.
6.解:如图,连接OB、OC,则∠BOC=90°,
根据圆周角定理,得:∠BPC=∠BOC=45°.
故选:B.
7.解:如图,连接OM,
∵正六边形OABCDE,
∴∠FOG=120°,
∵点M为劣弧FG的中点,
∴∠FOM=60°,OM=OF,
∴△OFM是等边三角形,
∴OM=OF=FM=2.
则⊙O的半径为2.
故选:C.
8.解:连接OA、OB、OD,过O作OH⊥AB于H,如图所示:
则AH=BH=AB,
∵等边三角形ABC和正方形ADEF,都内接于⊙O,
∴∠AOB=120°,∠AOD=90°,
∵OA=OD=OB,
∴△AOD是等腰直角三角形,∠AOH=∠BOH=×120°=60°,
∴AD=OA,AH=OA,
∴AB=2AH=2×OA=OA,
∴==,
故选:B.
9.解:如图所示,连接OB、OC,过O作OG⊥BC于G,
∵此多边形是正六边形,
∴△OBC是等边三角形,
∴∠OBG=60°,
∴边心距OG=2
故答案为:2.
10.解:∵六边形ABCDEF是正六边形,
∴AB=BC=AF,∠ABC=∠BAF=120°,
∴∠ABF=∠BAC=∠BCA=30°,
∴AG=BG,∠CBG=90°,
∴CG=2BG=2AG,
∴=;
故答案为:.
11.解:∵五边形ABCDE是⊙O的内接正五边形,
∴五边形ABCDE的中心角∠COD的度数为=72°,
故答案为:72°.
12.解:作正八边形ABCDEFGH的外接圆O.连接OA、OB,
∵八边形ABCDEFGH是OO内接正八边形,
∴∠AOB==45°,
由圆周角定理得,
∠AFO=∠AOB==22.5°,
故选答案为22.5°.
13.解:连接AE,DF,EC,
∵正六边形ABCDEF的边长为2,延长BA,EF交于点O,
∴可得:△AOF是等边三角形,则AO=FO=FA=2,
∵以O为原点,以边AB所在的直线为x轴建立平面直角坐标系,∠EOA=60°,EO=FO+EF=4,
∴∠EAO=90°,∠OEA=30°,故AE=4cos30°=6,
∴F(,3),D(4,6),E(2,6),
同理可得:C点坐标为:(5,3),
设直线DF的解析式为:y=kx+b,
则,
解得:,
故直线DF的解析式为:y=x+2,
设直线EC的解析式为:y=ax+c,
,
解得:,
故直线EC的解析式为:y=﹣x+8,
则x+2=﹣x+8,
解得:x=3,
则y=5,
∴直线DF与直线CE的交点坐标是:(3,5).
故答案为:(3,5).
14.解:设圆心是O,连接OA,OB,作OC于BC垂直.
设长方形的摊位长是2xm,
在直角△OAD中,∠AOD=30°,AD=xm,
则OD=xm,
在直角△OBC中,OC==,
∵OC﹣OD=CD=,
∴﹣x=,
解得:x=或(舍弃)
则2x=.
故答案是:.
15.解:连接PA,PO,
∵正六边形OABCDE的外接圆心是P,
∴∠OPA==60°,PO=PA,
∴△POA是等边三角形,
∴PO=PA=OA=6,
过P作PH⊥OA于H,则∠OPH=∠OPA=30°,OH=OA=3,
∴PH===3,
∴P的坐标是(3,3),
故答案为:(3,3).
16.解:圆O从A点出发,沿A→B→C→D→E→A顺时针在正五边形的边上滚动,
∵圆O的周长是1cm,正五边形ABCDE的边长是4cm,
∴圆在边上转了4×5=20圈,
而圆从一边转到另一边时,圆心绕五边形的一个顶点旋转了五边形的一个外角的度数,
∴圆绕五个顶点共旋转了360°,即它转了一圈,
∴圆回到原出发位置时,共转了21圈.
故答案为:21.
17.解:如图所示,连接OC、OB,过O作ON⊥CE于N,
则CN=EN,
∵多边形ABCDEF是正六边形,
∴∠COB=60°,
∵OC=OB,
∴△COB是等边三角形,
∴∠OCM=60°,
∴OM=OC?sin∠OCM,
∴OC=,
∵∠OCN=30°,
∴ON=OC=,CN=ON=2,
∴CE=2CN=4,
即圆内接正三角形的边长是4,
故答案为:4.
18.(1)证明:如图1,连接DE,
∵四边形ABCD是正方形,
∴AC⊥BD,OB=OD=OC,
∴EB=ED,∠ODC=∠OCD=45°,
∴∠EBD=∠EDB,
∵点P是弧AD的中点,
∴∠PBD=∠ABD=×∠AOD=22.5°,
∴∠EDC=45°+22.5°=67.5°,
∴∠CED=180°﹣45°﹣67.5°=67.5°,
∴∠CED=∠EDC,
∴CE=CD;
(2)解:如图2,连接DE,DP,
∵四边形ABCD是正方形,
∴∠BAD=∠EOD=90°,OA=OD,
∴∠P=∠BAD=90°,
∵PE=OE,
∴∠PDE=∠2,由(1)知∠1=∠2,
∴∠1=∠2=∠PDE,
∴∠1+∠2+∠PDE=90°,
∴∠2=30°,
∴OE=DE,
∴DE=2OE,
∴OD==OE,
∴=,
∴OD=OA=OE,
∴AE=OA﹣OE=(﹣1)OE,EC=OE+OC=(+1)OE,
∴==2﹣.
19.解:(1)∠AOQ=60°.
在△ABP和△BCQ中,.
∴△ABP≌△BCQ(SAS).
∴∠BAP=∠CBQ.
∴∠AOQ=∠ABO+∠BAP=∠ABO+∠CBQ=∠ABC=60°;
(2)理由同(1):正方形∠AOQ=90°,正五边形∠AOQ=108°,
(3)正n边形∠AOQ=.
故答案为:90°,108°.
20.证明:(1)延长BP至E,使PE=PC,
连接CE.∵∠1=∠2=60°,∠3=∠4=60°,
∴∠CPE=60°,
∴△PCE是等边三角形,
∴CE=PC,∠E=∠3=60°;
又∵∠EBC=∠PAC,
∴△BEC≌△APC,
∴PA=BE=PB+PC.
(2)过点B作BE⊥PB交PA于E.
∵∠1+∠2=∠2+∠3=90°
∴∠1=∠3,
又∵∠APB=45°,
∴BP=BE,∴;
又∵AB=BC,
∴△ABE≌△CBP,
∴PC=AE.
∴.
(3)答:;
证明:在AP上截取AQ=PC,
连接BQ,∵∠BAP=∠BCP,AB=BC,
∴△ABQ≌△CBP,
∴BQ=BP.
又∵∠APB=30°,
∴
∴
21.(1)证明:连接OF,AO,
∵AB=AF=EF,
∴==,
∴∠ABF=∠AFB=∠EBF=30°,
∵OB=OF,
∴∠OBF=∠BFO=30°,
∴∠ABF=∠OFB,
∴AB∥OF,
∵FG⊥BA,
∴OF⊥FG,
∴FG是⊙O的切线;
(2)解:∵==,
∴∠AOF=60°,
∵OA=OF,
∴△AOF是等边三角形,
∴∠AFO=60°,
∴∠AFG=30°,
∵FG=2,
∴AF=4,
∴AO=4,
∵AF∥BE,
∴S△ABF=S△AOF,
∴图中阴影部分的面积==.
22.解:(1)由正多边形的定义:各个角都相等,各条边都相等的多边形叫做正多边形;
故答案为:各个角;各条边;
(2)如图,
∵AB=2,BC=2,CD=2,DE=2,EF=2,FA=2,
∴AB=BC=CD=DE=EF=FA,
∵网格是等边三角形的网格,
∴∠FAB=2×60°=120°,
同理:∠ABC=∠BCD=∠CDE=∠DEF=∠EFA=120°,
∴∠FAB=∠ABC=∠BCD=∠CDE=∠DEF=∠EFA=120°,
∴六边形ABCDEFA是正六边形.
最大面积为24×=6;
(3)正六边形的对角线条数为=9,
∵多边形的外角和是360°,
∴正六边形的外角和为360°,
故答案为:9;360°.
一、选择题
1.如图,正方形ABCD内接于⊙O.点E为上一点,连接BE、CE,若∠CBE=15°,BE=3,则BC的长为( )
A.
B.
C.
D.
2.如图,将边长相等的正方形、正五边形、正六边形纸板,按如图方式放在桌面上,则∠a的度数是( )
A.42°
B.40°
C.36°
D.32°
3.正多边形的内切圆与外接圆的半径之比为,则这个正多边形为( )
A.正十二边形
B.正六边形
C.正四边形
D.正三角形
4.如图,若⊙O是正方形ABCD与正六边形AEFCGH的外接圆,则正方形ABCD与正六边形AEFCGH的周长之比为( )
A.2:3
B.:1
C.:
D.1:
5.如图,正方形ABCD内接于⊙O,线段MN在对角线BD上运动,若⊙O的面积为2π,MN=1,则△AMN周长的最小值是( )
A.3
B.4
C.5
D.6
6.如图,四边形ABCD是⊙O的内接正方形,点P是上不同于点C的任意一点,则∠BPC的大小是( )
A.22.5°
B.45°
C.30°
D.50°
7.如图,⊙O与正六边形OABCDE的边OA、OE分别交于点F、G,点M为劣弧FG的中点.若FM=2,则⊙O的半径为( )
A.2
B.
C.2
D.2
8.如图,等边三角形ABC和正方形ADEF都内接于⊙O,则AD:AB=( )
A.2:
B.:
C.:
D.:2
二、填空题
9.若某正六边形的边长是4,则该正六边形的边心距为
.
10.如图,在正六边形ABCDEF中,AC于FB相交于点G,则值为
.
11.如图,五边形ABCDE是⊙O的内接正五边形,则∠COD的度数是
.
12.如图,点O为正八边形ABCDEFGH的中心,则∠AFO的度数为
.
13.如图,正六边形ABCDEF的边长为2,延长BA,EF交于点O,以O为原点,以边AB所在的直线为x轴建立平面直角坐标系,则直线DF与直线EC的交点坐标是
.
14.如图为一个半径为5m的圆形广场,其中放有六个宽为m的长方形临时摊位,这些摊位均有两个顶点在广场边上,另两个顶点紧靠相邻摊位的顶点,则每个长方形摊位的长为
m.
15.如图,在平面直角坐标系中,正六边形OABCDE边长是6,则它的外接圆心P的坐标是
.
16.如图,圆O的周长是1cm,正五边形ABCDE的边长是4cm,圆O从A点出发,沿A→B→C→D→E→A顺时针在正五边形的边上滚动,当回到出发点时,则圆O共滚动了
周.
17.圆内接正六边形的边心距为2,则此圆内接正三角形的边长是
.
三、解答题
18.已知,正方形ABCD内接于⊙O,点P是弧AD上一点.
(1)如图1,若点P是弧AD的中点,求证:CE=CD;
(2)如图2,若图中PE=OE,求的值.
19.如图1,△ABC为等边三角形,图2为正方形,图3为正五边形,图4为正多边形.
(1)如图1当BP=CQ时,请求出∠AOQ的度数,并说明理由
(2)如图2,在正方形中,当BP=CQ时∠AOQ=
;如图3,在正五边形中,当BP=CQ时,∠AOQ=
;
(3)如图4,在正n边形中,当BP=CQ时,∠AOQ是否有什么规律?如果有请用含有n的式子直接表示;如果没有规律,请说明理由.
20.(1)已知:如图1,△ABC是⊙O的内接正三角形,点P为上一动点,求证:PA=PB+PC.
下面给出一种证明方法,你可以按这一方法补全证明过程,也可以选择另外的证明方法.
证明:在AP上截取AE=CP,连接BE
∵△ABC是正三角形
∴AB=CB
∵∠1和∠2的同弧圆周角
∴∠1=∠2
∴△ABE≌△CBP
(2)如图2,四边形ABCD是⊙O的内接正方形,点P为上一动点,求证:PA=PC+PB.
(3)如图3,六边形ABCDEF是⊙O的内接正六边形,点P为上一动点,请探究PA、PB、PC三者之间有何数量关系,直接写出结论.
21.如图,正六边形ABCDEF内接于⊙O,BE是⊙O的直径,连接BF,延长BA,过F作FG⊥BA,垂足为G.
(1)求证:FG是⊙O的切线;
(2)已知FG=2,求图中阴影部分的面积.
22.探究题:
(1)
都相等,
都相等的多边形叫做正多边形;
(2)如图,格点长方形MNPQ的各点分布在边长均为1的等边三角形组成的网格上,请在格点长方形MNPQ内画出一个面积最大的格点正六边形ABCDEF,并简要说明它是正六边形的理由;
(3)正六边形有
条对角线,它的外角和为
度.
参考答案
1.解:连接OA,OB,OE,
∵正方形ABCD内接于⊙O,
∴OA=OB=OE,∠AOB==90°,AB=BC,∠ABC=90°,
∴∠OAB=∠OBA=(180°﹣∠AOB)=45°,
∴∠OBC=∠ABC﹣∠OBA=45°,
∵∠CBE=15°,
∴∠OBE=∠OBC+∠CBE=60°,
∴△OBE是等边三角形,
∴OB=BE=3,
∴OA=3,
∴AB==3,
∴BC=3,
故选:D.
2.解:正方形的内角为90°,
正五边形的内角为=108°,
正六边形的内角为=120°,
∠1=360°﹣90°﹣108°﹣120°=42°,
故选:A.
3.解:如图,设AB是正多边形的一边,O为正多边形的内切圆与外接圆的圆心,OC⊥AB于C,
∵正多边形的内切圆与外接圆的半径之比为,
∴=,
在Rt△AOC中,cos∠AOC==,
∴∠AOC=45°,
∴∠AOB=2∠AOC=90°,
则正多边形边数为:=4.
故选:C.
4.解:连接OA、OB.OE,如图所示:
设此圆的半径为R,
则它的内接正方形的边长为R,它的内接正六边形的边长为R,
∴内接正方形和内接正六边形的边长之比为R:R=:1,
∴正方形ABCD与正六边形AEFCGH的周长之比=内接正方形和内接正六边形的边长之比=4:6=2:3,
故选:A.
5.解:⊙O的面积为2π,则圆的半径为,则BD=2=AC,
由正方形的性质,知点C是点A关于BD的对称点,
过点C作CA′∥BD,且使CA′=1,
连接AA′交BD于点N,取NM=1,连接AM、CM,则点M、N为所求点,
理由:∵A′C∥MN,且A′C=MN,则四边形MCA′N为平行四边形,
则A′N=CM=AM,
故△AMN的周长=AM+AN+MN=AA′+1为最小,
则A′A==3,
则△AMN的周长的最小值为3+1=4,
故选:B.
6.解:如图,连接OB、OC,则∠BOC=90°,
根据圆周角定理,得:∠BPC=∠BOC=45°.
故选:B.
7.解:如图,连接OM,
∵正六边形OABCDE,
∴∠FOG=120°,
∵点M为劣弧FG的中点,
∴∠FOM=60°,OM=OF,
∴△OFM是等边三角形,
∴OM=OF=FM=2.
则⊙O的半径为2.
故选:C.
8.解:连接OA、OB、OD,过O作OH⊥AB于H,如图所示:
则AH=BH=AB,
∵等边三角形ABC和正方形ADEF,都内接于⊙O,
∴∠AOB=120°,∠AOD=90°,
∵OA=OD=OB,
∴△AOD是等腰直角三角形,∠AOH=∠BOH=×120°=60°,
∴AD=OA,AH=OA,
∴AB=2AH=2×OA=OA,
∴==,
故选:B.
9.解:如图所示,连接OB、OC,过O作OG⊥BC于G,
∵此多边形是正六边形,
∴△OBC是等边三角形,
∴∠OBG=60°,
∴边心距OG=2
故答案为:2.
10.解:∵六边形ABCDEF是正六边形,
∴AB=BC=AF,∠ABC=∠BAF=120°,
∴∠ABF=∠BAC=∠BCA=30°,
∴AG=BG,∠CBG=90°,
∴CG=2BG=2AG,
∴=;
故答案为:.
11.解:∵五边形ABCDE是⊙O的内接正五边形,
∴五边形ABCDE的中心角∠COD的度数为=72°,
故答案为:72°.
12.解:作正八边形ABCDEFGH的外接圆O.连接OA、OB,
∵八边形ABCDEFGH是OO内接正八边形,
∴∠AOB==45°,
由圆周角定理得,
∠AFO=∠AOB==22.5°,
故选答案为22.5°.
13.解:连接AE,DF,EC,
∵正六边形ABCDEF的边长为2,延长BA,EF交于点O,
∴可得:△AOF是等边三角形,则AO=FO=FA=2,
∵以O为原点,以边AB所在的直线为x轴建立平面直角坐标系,∠EOA=60°,EO=FO+EF=4,
∴∠EAO=90°,∠OEA=30°,故AE=4cos30°=6,
∴F(,3),D(4,6),E(2,6),
同理可得:C点坐标为:(5,3),
设直线DF的解析式为:y=kx+b,
则,
解得:,
故直线DF的解析式为:y=x+2,
设直线EC的解析式为:y=ax+c,
,
解得:,
故直线EC的解析式为:y=﹣x+8,
则x+2=﹣x+8,
解得:x=3,
则y=5,
∴直线DF与直线CE的交点坐标是:(3,5).
故答案为:(3,5).
14.解:设圆心是O,连接OA,OB,作OC于BC垂直.
设长方形的摊位长是2xm,
在直角△OAD中,∠AOD=30°,AD=xm,
则OD=xm,
在直角△OBC中,OC==,
∵OC﹣OD=CD=,
∴﹣x=,
解得:x=或(舍弃)
则2x=.
故答案是:.
15.解:连接PA,PO,
∵正六边形OABCDE的外接圆心是P,
∴∠OPA==60°,PO=PA,
∴△POA是等边三角形,
∴PO=PA=OA=6,
过P作PH⊥OA于H,则∠OPH=∠OPA=30°,OH=OA=3,
∴PH===3,
∴P的坐标是(3,3),
故答案为:(3,3).
16.解:圆O从A点出发,沿A→B→C→D→E→A顺时针在正五边形的边上滚动,
∵圆O的周长是1cm,正五边形ABCDE的边长是4cm,
∴圆在边上转了4×5=20圈,
而圆从一边转到另一边时,圆心绕五边形的一个顶点旋转了五边形的一个外角的度数,
∴圆绕五个顶点共旋转了360°,即它转了一圈,
∴圆回到原出发位置时,共转了21圈.
故答案为:21.
17.解:如图所示,连接OC、OB,过O作ON⊥CE于N,
则CN=EN,
∵多边形ABCDEF是正六边形,
∴∠COB=60°,
∵OC=OB,
∴△COB是等边三角形,
∴∠OCM=60°,
∴OM=OC?sin∠OCM,
∴OC=,
∵∠OCN=30°,
∴ON=OC=,CN=ON=2,
∴CE=2CN=4,
即圆内接正三角形的边长是4,
故答案为:4.
18.(1)证明:如图1,连接DE,
∵四边形ABCD是正方形,
∴AC⊥BD,OB=OD=OC,
∴EB=ED,∠ODC=∠OCD=45°,
∴∠EBD=∠EDB,
∵点P是弧AD的中点,
∴∠PBD=∠ABD=×∠AOD=22.5°,
∴∠EDC=45°+22.5°=67.5°,
∴∠CED=180°﹣45°﹣67.5°=67.5°,
∴∠CED=∠EDC,
∴CE=CD;
(2)解:如图2,连接DE,DP,
∵四边形ABCD是正方形,
∴∠BAD=∠EOD=90°,OA=OD,
∴∠P=∠BAD=90°,
∵PE=OE,
∴∠PDE=∠2,由(1)知∠1=∠2,
∴∠1=∠2=∠PDE,
∴∠1+∠2+∠PDE=90°,
∴∠2=30°,
∴OE=DE,
∴DE=2OE,
∴OD==OE,
∴=,
∴OD=OA=OE,
∴AE=OA﹣OE=(﹣1)OE,EC=OE+OC=(+1)OE,
∴==2﹣.
19.解:(1)∠AOQ=60°.
在△ABP和△BCQ中,.
∴△ABP≌△BCQ(SAS).
∴∠BAP=∠CBQ.
∴∠AOQ=∠ABO+∠BAP=∠ABO+∠CBQ=∠ABC=60°;
(2)理由同(1):正方形∠AOQ=90°,正五边形∠AOQ=108°,
(3)正n边形∠AOQ=.
故答案为:90°,108°.
20.证明:(1)延长BP至E,使PE=PC,
连接CE.∵∠1=∠2=60°,∠3=∠4=60°,
∴∠CPE=60°,
∴△PCE是等边三角形,
∴CE=PC,∠E=∠3=60°;
又∵∠EBC=∠PAC,
∴△BEC≌△APC,
∴PA=BE=PB+PC.
(2)过点B作BE⊥PB交PA于E.
∵∠1+∠2=∠2+∠3=90°
∴∠1=∠3,
又∵∠APB=45°,
∴BP=BE,∴;
又∵AB=BC,
∴△ABE≌△CBP,
∴PC=AE.
∴.
(3)答:;
证明:在AP上截取AQ=PC,
连接BQ,∵∠BAP=∠BCP,AB=BC,
∴△ABQ≌△CBP,
∴BQ=BP.
又∵∠APB=30°,
∴
∴
21.(1)证明:连接OF,AO,
∵AB=AF=EF,
∴==,
∴∠ABF=∠AFB=∠EBF=30°,
∵OB=OF,
∴∠OBF=∠BFO=30°,
∴∠ABF=∠OFB,
∴AB∥OF,
∵FG⊥BA,
∴OF⊥FG,
∴FG是⊙O的切线;
(2)解:∵==,
∴∠AOF=60°,
∵OA=OF,
∴△AOF是等边三角形,
∴∠AFO=60°,
∴∠AFG=30°,
∵FG=2,
∴AF=4,
∴AO=4,
∵AF∥BE,
∴S△ABF=S△AOF,
∴图中阴影部分的面积==.
22.解:(1)由正多边形的定义:各个角都相等,各条边都相等的多边形叫做正多边形;
故答案为:各个角;各条边;
(2)如图,
∵AB=2,BC=2,CD=2,DE=2,EF=2,FA=2,
∴AB=BC=CD=DE=EF=FA,
∵网格是等边三角形的网格,
∴∠FAB=2×60°=120°,
同理:∠ABC=∠BCD=∠CDE=∠DEF=∠EFA=120°,
∴∠FAB=∠ABC=∠BCD=∠CDE=∠DEF=∠EFA=120°,
∴六边形ABCDEFA是正六边形.
最大面积为24×=6;
(3)正六边形的对角线条数为=9,
∵多边形的外角和是360°,
∴正六边形的外角和为360°,
故答案为:9;360°.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
