苏教版数学五年级上册 七 解决问题的策略 复习 课件(共27张PPT)
文档属性
| 名称 | 苏教版数学五年级上册 七 解决问题的策略 复习 课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 624.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-22 07:28:55 | ||
图片预览







文档简介
(共27张PPT)
七
解决问题的策略
复习课件
本节课知识点:
1.明确有些实际问题可以通过列举来解决,并按照一定的顺序列举,对列举结果进行比较,作出选择。
2.能够根据问题的特点,选择合适的列举方法。列举过程中,可以列表,也可以画图,对列举的全部结果,要进行检查。
复习旧知
同学们,通过本单元的学习,你掌握了哪些解决问题的方法?
在解决问题时,可以根据问题的特点,选择合适的列举方法,做到按一定的顺序,不重复、不遗漏,并对结果进行检查。
巩固练习
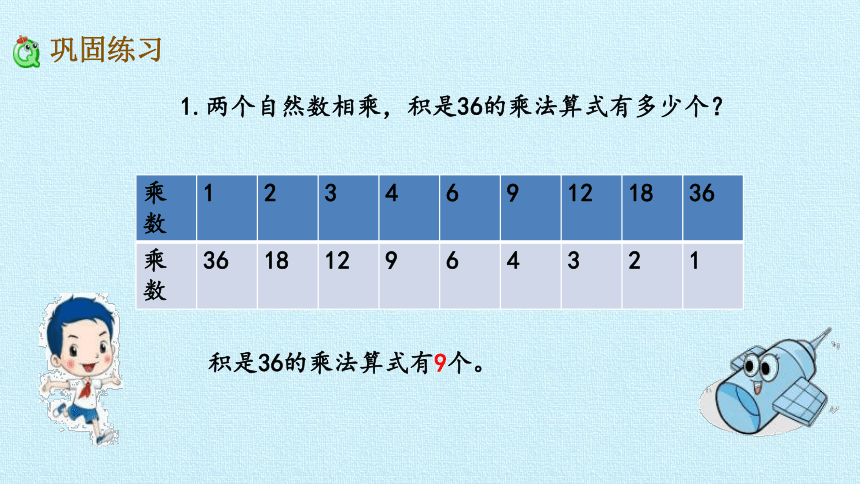
1.两个自然数相乘,积是36的乘法算式有多少个?
乘
数
1
2
3
4
6
9
12
18
36
乘
数
36
18
12
9
6
4
3
2
1
积是36的乘法算式有9个。
2.有A、B、C三个网站,分别是每两天、三天、四天更新一次。某月1日三个网站同时更新后,到这个月15日,哪几天没有网站更新?哪一天三个网站同时更新?
日期
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
A网站
B网站
C网站
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
到这个月15日,哪几天没有网站更新?哪一天三个网站同时更新?
到这个月15日,2日,6日,8日,12日,14日这五天没有网站更新,13日三个网站同时更新。
3.用
、
、
这三张数字卡片一共能组成多少个不同的三位数?
8
2
5
2
8
5
2
8
5
8
2
5
8
2
5
8
5
2
8
5
2
答:一共能组成6个不同的三位数。
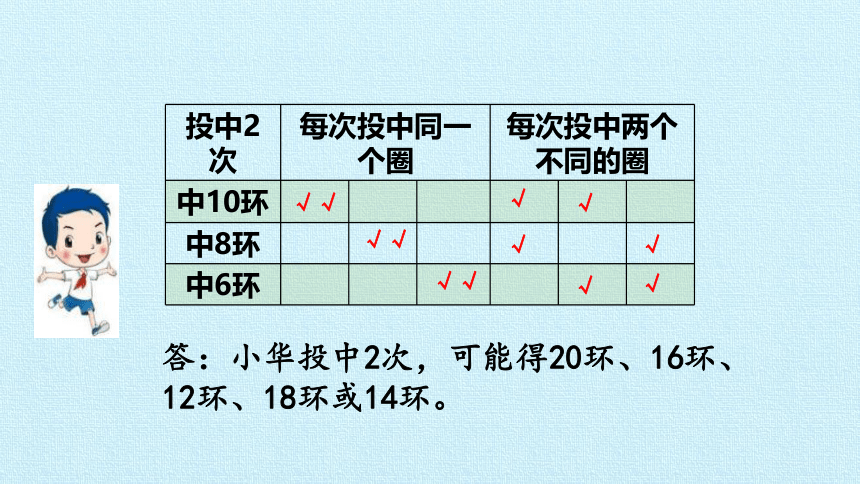
4.一张靶纸共三圈,投中内圈10环,投中中圈得8环,投中外圈得6环。小华投中1次,可能得多少环?投中2次呢?
投中1次可能得10环、8环、6环。
投中2次
每次投中同一个圈
每次投中两个不同的圈
中10环
中8环
中6环
√√
√√
√√
√
√
√
√
√
√
答:小华投中2次,可能得20环、16环、12环、18环或14环。
5.在右面的图形中再给2个格子涂上颜色,使涂色部分成为一个轴对称图形。有几种不同的涂法?
答:有5种不同的涂法。
6.图中一共有多少个正方形?
一共有14个正方形。先数小正方形,共9个,再数由4个小正方形组成的较大正方形,共4个,最后加上最大的1个正方形,总共是14个正方形。
7.小红和小力各有
、
、
三张数字卡片,每人拿出1张,一共有多少种不同的拿法?
8
2
5
8
8
2
8
5
8
8
2
2
2
5
2
8
5
2
5
5
5
一共有9种不同放入拿法。
这节课你们都学会了哪些知识?
课堂小结
列举
一一列举策略齐,列表画图有条理,
不重复来不遗漏,直观形象解难题。
达标检测
1.周长是50的长方形,当长是16米时,宽是(
)米,面积是(
)平方米;当宽是5米时,长是(
)米,面积是(
)平方米。
【考点提示】
本题考查长方形的周长一定时面积不一定相等。
【解题思路】
长方形的周长是两个长和宽的和,那么长方形的宽=周长÷2一长=50÷2-16=9(米),长方形的面积=长×宽=16×9=144(平方米);同理,如果宽是5米,长=周长÷2一宽=
50÷2-5=20(米),面积=长×宽=20×5=100(平方米)。
2.拉萨路小学组织了音乐、美术、象棋三种兴趣小组,每人必须选一种或几种,一个人一共有(
)种不同的参加方法。
【考点提示】
本题考查解决问题的策略一列举法。
【解题思路】
三种兴趣小组中,如果每人选一种,有3种参加方法;如果每人选2种有3种参加方法:音乐小组和美术小组、音乐小组和象棋小组、美术小组和象棋小组;如果每人选3种只有1种参加方法,这样一共有3+3+1=7(种)参加方法。
3.如图,小华从家到少年宫,如果只能向南走或向西走,一共有(
)种不同的路线可走。
【考点提示】
本题考查解决问题的策略——列举法。
【解题思路】
先分清方向:上北下南左西右东。依据题意,小华只能向南或向西走,我们采用列举法,可以看出一共有6种不同的路线可走。
4.元旦期间,王亮约了两位同学去公园游玩,他们见面后互相问候,那么他们一共问候了(
)声。
【考点提示】
本题考查解决问题的策略一列举法。
【解题思路】
我们把王亮和其他两位同学分别用A、B、C表示,他们见面后要互相问候,那么A与B、A与C、B与C一共问候3次,同样B与A、C与A、C与B也要问候3次,这样他们一共问候了6次。
5.一辆列车,从上海开往南京,中途停靠苏州、无锡、常州、镇江四个站点,那么铁路部门为这趟列车需要准备(
)种不同的车票。
A.30
B.15
C.5
D.10
【考点提示】
本题考查简单的排列组合问题一列举法。
【解题思路】
这辆列车从上海开往南京,中途停靠四个站点,这六个站点分别用1、2、3、4、5、6来表示,需要准备的车票有:1和2、1和3、1和4、1和5、1和6、2和3、2和4、2和5、2和6、3和4、
3和5、3和6、4和5、4和6、5和6共十五种车票。
6.如右图,横向或竖向每相邻两个点之间的距离表示1厘米,如果要在图中画一个面积是1平方厘米的平行四边形(平行四边形的顶点要在点上,不包括长方形),那么一共可以画(
)个。
A.4
B.6
C.5
D.8
【考点提示】
本题考查解决问题的策略一连线列举法。
【解题思路】
平行四边形的面积是底乘高,面积是1平方厘米,底和高必须各是1厘米。按照这样的方法一共可以连出8个面积是1平方厘米的平行四边形。
谢
谢
七
解决问题的策略
复习课件
本节课知识点:
1.明确有些实际问题可以通过列举来解决,并按照一定的顺序列举,对列举结果进行比较,作出选择。
2.能够根据问题的特点,选择合适的列举方法。列举过程中,可以列表,也可以画图,对列举的全部结果,要进行检查。
复习旧知
同学们,通过本单元的学习,你掌握了哪些解决问题的方法?
在解决问题时,可以根据问题的特点,选择合适的列举方法,做到按一定的顺序,不重复、不遗漏,并对结果进行检查。
巩固练习
1.两个自然数相乘,积是36的乘法算式有多少个?
乘
数
1
2
3
4
6
9
12
18
36
乘
数
36
18
12
9
6
4
3
2
1
积是36的乘法算式有9个。
2.有A、B、C三个网站,分别是每两天、三天、四天更新一次。某月1日三个网站同时更新后,到这个月15日,哪几天没有网站更新?哪一天三个网站同时更新?
日期
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
A网站
B网站
C网站
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
到这个月15日,哪几天没有网站更新?哪一天三个网站同时更新?
到这个月15日,2日,6日,8日,12日,14日这五天没有网站更新,13日三个网站同时更新。
3.用
、
、
这三张数字卡片一共能组成多少个不同的三位数?
8
2
5
2
8
5
2
8
5
8
2
5
8
2
5
8
5
2
8
5
2
答:一共能组成6个不同的三位数。
4.一张靶纸共三圈,投中内圈10环,投中中圈得8环,投中外圈得6环。小华投中1次,可能得多少环?投中2次呢?
投中1次可能得10环、8环、6环。
投中2次
每次投中同一个圈
每次投中两个不同的圈
中10环
中8环
中6环
√√
√√
√√
√
√
√
√
√
√
答:小华投中2次,可能得20环、16环、12环、18环或14环。
5.在右面的图形中再给2个格子涂上颜色,使涂色部分成为一个轴对称图形。有几种不同的涂法?
答:有5种不同的涂法。
6.图中一共有多少个正方形?
一共有14个正方形。先数小正方形,共9个,再数由4个小正方形组成的较大正方形,共4个,最后加上最大的1个正方形,总共是14个正方形。
7.小红和小力各有
、
、
三张数字卡片,每人拿出1张,一共有多少种不同的拿法?
8
2
5
8
8
2
8
5
8
8
2
2
2
5
2
8
5
2
5
5
5
一共有9种不同放入拿法。
这节课你们都学会了哪些知识?
课堂小结
列举
一一列举策略齐,列表画图有条理,
不重复来不遗漏,直观形象解难题。
达标检测
1.周长是50的长方形,当长是16米时,宽是(
)米,面积是(
)平方米;当宽是5米时,长是(
)米,面积是(
)平方米。
【考点提示】
本题考查长方形的周长一定时面积不一定相等。
【解题思路】
长方形的周长是两个长和宽的和,那么长方形的宽=周长÷2一长=50÷2-16=9(米),长方形的面积=长×宽=16×9=144(平方米);同理,如果宽是5米,长=周长÷2一宽=
50÷2-5=20(米),面积=长×宽=20×5=100(平方米)。
2.拉萨路小学组织了音乐、美术、象棋三种兴趣小组,每人必须选一种或几种,一个人一共有(
)种不同的参加方法。
【考点提示】
本题考查解决问题的策略一列举法。
【解题思路】
三种兴趣小组中,如果每人选一种,有3种参加方法;如果每人选2种有3种参加方法:音乐小组和美术小组、音乐小组和象棋小组、美术小组和象棋小组;如果每人选3种只有1种参加方法,这样一共有3+3+1=7(种)参加方法。
3.如图,小华从家到少年宫,如果只能向南走或向西走,一共有(
)种不同的路线可走。
【考点提示】
本题考查解决问题的策略——列举法。
【解题思路】
先分清方向:上北下南左西右东。依据题意,小华只能向南或向西走,我们采用列举法,可以看出一共有6种不同的路线可走。
4.元旦期间,王亮约了两位同学去公园游玩,他们见面后互相问候,那么他们一共问候了(
)声。
【考点提示】
本题考查解决问题的策略一列举法。
【解题思路】
我们把王亮和其他两位同学分别用A、B、C表示,他们见面后要互相问候,那么A与B、A与C、B与C一共问候3次,同样B与A、C与A、C与B也要问候3次,这样他们一共问候了6次。
5.一辆列车,从上海开往南京,中途停靠苏州、无锡、常州、镇江四个站点,那么铁路部门为这趟列车需要准备(
)种不同的车票。
A.30
B.15
C.5
D.10
【考点提示】
本题考查简单的排列组合问题一列举法。
【解题思路】
这辆列车从上海开往南京,中途停靠四个站点,这六个站点分别用1、2、3、4、5、6来表示,需要准备的车票有:1和2、1和3、1和4、1和5、1和6、2和3、2和4、2和5、2和6、3和4、
3和5、3和6、4和5、4和6、5和6共十五种车票。
6.如右图,横向或竖向每相邻两个点之间的距离表示1厘米,如果要在图中画一个面积是1平方厘米的平行四边形(平行四边形的顶点要在点上,不包括长方形),那么一共可以画(
)个。
A.4
B.6
C.5
D.8
【考点提示】
本题考查解决问题的策略一连线列举法。
【解题思路】
平行四边形的面积是底乘高,面积是1平方厘米,底和高必须各是1厘米。按照这样的方法一共可以连出8个面积是1平方厘米的平行四边形。
谢
谢
