5.2 平面直角坐标系 同步练习(含答案)
文档属性
| 名称 | 5.2 平面直角坐标系 同步练习(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-22 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第五章
位置与坐标
2
平面直角坐标系
知识能力全练
知识点一
平面直角坐标系及其相关概念
1.平面直角坐标系的画法正确的是(
)
知识点二
点的坐标表示
2.在平面直角坐标系中,点P(x2+2,-3)所在的象限是(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
3.点P(-2021,2022)到x轴的距离为(
)
A.-2021
B.-2022
C.2021
D.2022
4.已知点P在第四象限,该点到x轴的距离为3,到y轴的距离为1,则点P的坐标为__________.
5.坐标平面内有4个点:A(1,2),B(0,2),C(0,-1),D(2,0).
(1)画出平面直角坐标系,描出上述四个点,并顺次连接A,B,C,D,A,得到四边形ABCD;
(2)求四边形ABCD的面积.
知识点三
特殊位置上点的坐标特征
6.已知点P(m+2,2m-4)在x轴上,则点P的坐标是(
)
A.(4,0)
B.(0,4)
C.(-4,0)
D.(0,-4)
7.若点A(m,n),点B(n,m)表示同一点,则这一点一定在(
)
A.第二、四象限的角平分线上
B.第一、三象限的角平分线上
C.平行于x轴的直线上
D.平行于y轴的直线上
8.若经过点A,B的直线垂直于x轴,且A(x+1,-2)、B(-4,1),则x=_________.
9.已知平面直角坐标系内的点P(3-a,2a+9)到两个坐标轴的距离相等,求点P的坐标.
知识点四
由点的坐标确定点的位置继而确定图形的形状
10.在如图所示的直角坐标系中描出下列各组点,并将各组内的点用线段依次连接起来.
(1)(2,0)、(6,0)、(6,1)、(5,0)、(6,-1)、(6,0);
(2)(2,0)、(5,3)、(4,0);
(3)(2,0)、(5,-3)、(4,0).
观察所得到的图形像什么?如果要将此图形向上平移到x轴上方,那么至少要向上平移几个(整数个)单位长度?
11.在如图所示的平面直角坐标系中,描出点A(-2,1),B(3,1),C(-2,-2),D(3,-2).
(1)顺次连接A、B、C、D四点,构成的图形像什么?
(2)线段AB、CD有什么关系?并说明理由.
知识点五
建立平面直角坐标系,确定点的坐标
12.已知A,B,C,D四位同学的家所在位置如图所示,若以A同学家的位置为坐标原点建立平面直角坐标系,C同学家的坐标为(1,5),则B,D两同学家的坐标分别为(
)
A.(2,3),(3,2)
B.(3,2),(2,3)
C.(2,3),(-3,2)
D.(3,2),(-2,3)
13.如图所示,已知棋子“车”的坐标为(-2,1),棋子“马”的坐标为(3,-1),则棋子“炮”的坐标为(
)
A.(1,1)
B.(2,1)
C.(2,2)
D.(3,1)
14.建立两个适当的平面直角坐标系,并分别表示出边长为8的正方形的顶点的坐标.
巩固提高全练
15.已知点A(6,8),B(1,2a),若直线AB∥x轴,则a的值为(
)
A.4
B.2
C.-4
D.-2
16.如果|3-a|+(b+5)2=0,那么点A(a,b)在(
)
A.第四象限
B.第三象限
C.第二象限
D.第一象限
17.如果P(m+3,2m+4)在y轴上,那么点P的坐标是___________.
18.在平面直角坐标系的第四象限内有一点M,到x轴的距离为4,到y轴的距离为5,则点M的坐标为(
)
A.(4,5)
B.(-5,4)
C.(4,-5)
D.(5,-4)
19.已知a+b>0,ab>0,则在如图所示的平面直角坐标系中,小手盖住的点的坐标可能是(
)
A.(a,b)
B.(-a,b)
C.(-a,-b)
D.(a,-b)
20.小明为画一个零件的轴截面,以该轴截面底边所在的直线为x轴,对称轴为y轴,建立如图所示的平面直角坐标系.若坐标轴的单位长度取1
mm,则图中转折点P的坐标是(
)
A.(5,30)
B.(8,10)
C.(9,10)
D.(10,10)
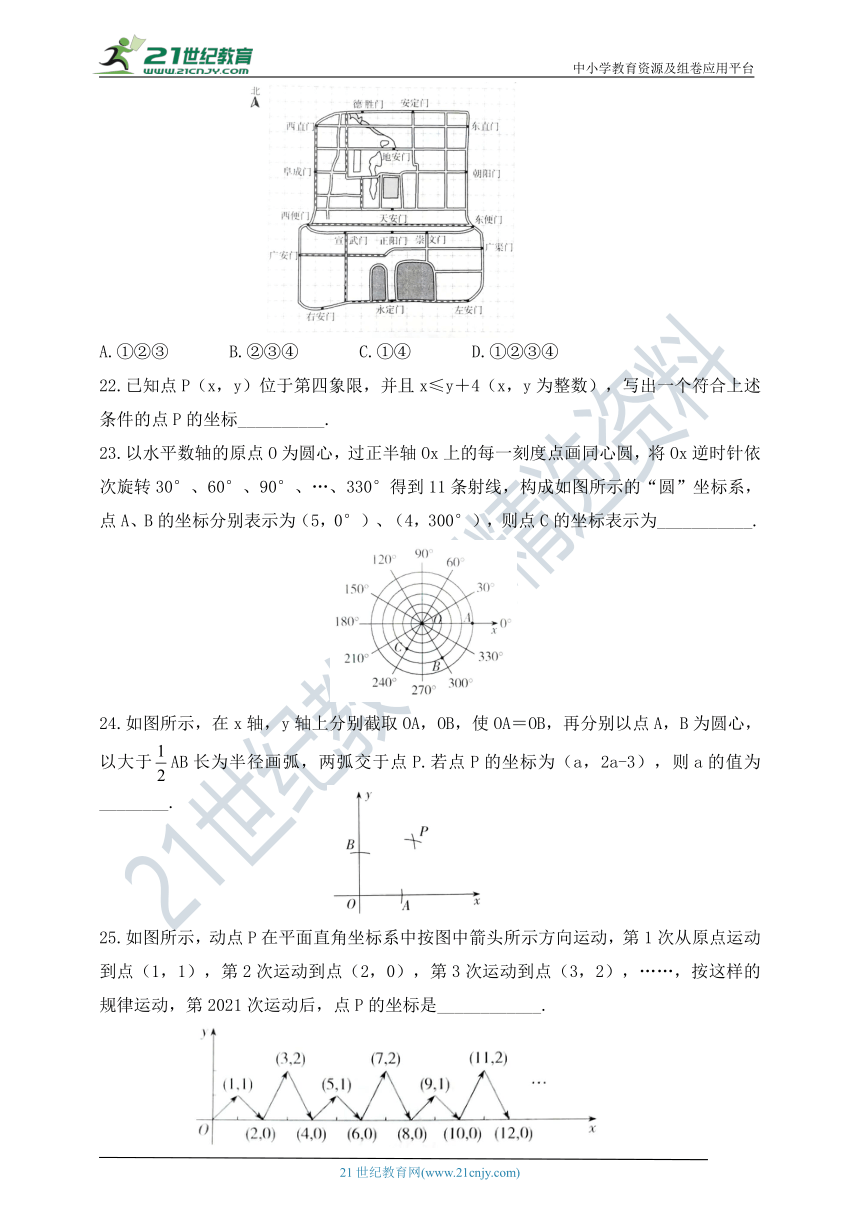
21.下图是老北京城一些地点的分布示意图.在图中,分别以正东、正北方向为x轴、y轴的正方向建立平面直角坐标系,有如下四个结论:
①当表示天安门的点的坐标为(0,0),表示广安门的点的坐标为(-6,-3)时,表示左安门的点的坐标为(5,-6);
②当表示天安门的点的坐标为(0,0),表示广安门的点的坐标为(-12,-6)时,表示左安门的点的坐标为(10,-12);
③当表示天安门的点的坐标为(1,1),表示广安门的点的坐标为(-11,-5)时,表示左安门的点的坐标为(11,-11);
④当表示天安门的点的坐标为(1.5,1.5),表示广安门的点的坐标为(-16.5,-7.5)时,表示左安门的点的坐标为(16.5,-16.5).
上述结论中,所有正确结论的序号是(
)
A.①②③
B.②③④
C.①④
D.①②③④
22.已知点P(x,y)位于第四象限,并且x≤y+4(x,y为整数),写出一个符合上述条件的点P的坐标__________.
23.以水平数轴的原点O为圆心,过正半轴Ox上的每一刻度点画同心圆,将Ox逆时针依次旋转30°、60°、90°、…、330°得到11条射线,构成如图所示的“圆”坐标系,点A、B的坐标分别表示为(5,0°)、(4,300°),则点C的坐标表示为___________.
24.如图所示,在x轴,y轴上分别截取OA,OB,使OA=OB,再分别以点A,B为圆心,以大于AB长为半径画弧,两弧交于点P.若点P的坐标为(a,2a-3),则a的值为________.
25.如图所示,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次运动到点(2,0),第3次运动到点(3,2),……,按这样的规律运动,第2021次运动后,点P的坐标是____________.
26.先阅读下面一段文字,再回答后面的问题.
已知在平面内两点P1(x1,y1)、P2(x2,y2),这两点间的距离公式为P1P2=,同时,当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2-x1|或|y2-y1|.
(1)已知A(2,4)、B(-3,-8),试求A、B两点间的距离;
(2)已知A、B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为-1,试求A、B两点间的距离;
(3)已知一个三角形各顶点坐标为A(0,6)、B(-3,2)、C(3,2),你能判断此三角形的形状吗?说明理由.
参考答案
1.B
2.D
3.D
4.(1,-3)
5.解析
(1)如图所示.
(2)由图可知,S四边形ABCD=S梯形AB0D+S△COD=×(1+2)×2+×1×2=3+1=4.
6.A
7.B
8.
-5
9.解析
∵点P(3-a,2a+9)到两个坐标轴的距离相等,
∴3-a=2a+9或3-a+2a+9=0,解得a=-2或a=-12.
当a=-2时,3-a=5,2a+9=5,此时,点P的坐标为(5,5);
当a=-12时,3-a=15,2a+9=-15,此时,点P的坐标为(15,-15).
综上所述,点P的坐标为(5,5)或(15,-15).
10.解析
如图所示.
图形像一条金鱼,要将此图形向上平移到x轴上方,那么至少要向上平移4个单位长度.
11.解析
描点如图.
(1)顺次连接A、B、C、D四点,构成的图形像字母“Z”.
(2)AB∥CD,AB=CD.
理由如下:
∵A(-2,1),B(3,1),∴A,B两点的纵坐标相同.
∴AB∥x轴.同理,CD∥x轴.∴AB∥CD.
由A(-2,1),B(3,1),C(-2,-2),D(3,-2)得,AB=5,CD=5,∴AB=CD.
12.D
13.B
14.解析
答案不唯一如图1,以正方形两邻边所在的直线为坐标轴,建立平面直角坐标系,则A(8,0),B(8,8),C(0,8),O(0,0).
如图2,以正方形的两条对称轴所在的直线为坐标轴,建立平面直角坐标系,则A(4,4),B(4,4),C(-4,4),D(-4,-4).
15.A
16.A
17.(0,-2)
18.D
19.B
20.C
21.D
22.(1,-2)(答案不唯一)
23.(3,240°)
24.
3
25.(2021,1)
26.解析
(1)∵A(2,4)、B(-3,-8),
∴AB==13,即A、B两点间的距离是13.
(2)∵A、B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为-1,
∴AB=|-1-5|=6,即A、B两点间的距离是6.
(3)能,△ABC是等腰三角形理由:∵一个三角形各顶点坐标为A(0,6)、B(-3,2)、C(3,2),∴AB=5,BC=6,AC=5,∴AB=AC,∴△ABC是等腰三角形.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
第五章
位置与坐标
2
平面直角坐标系
知识能力全练
知识点一
平面直角坐标系及其相关概念
1.平面直角坐标系的画法正确的是(
)
知识点二
点的坐标表示
2.在平面直角坐标系中,点P(x2+2,-3)所在的象限是(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
3.点P(-2021,2022)到x轴的距离为(
)
A.-2021
B.-2022
C.2021
D.2022
4.已知点P在第四象限,该点到x轴的距离为3,到y轴的距离为1,则点P的坐标为__________.
5.坐标平面内有4个点:A(1,2),B(0,2),C(0,-1),D(2,0).
(1)画出平面直角坐标系,描出上述四个点,并顺次连接A,B,C,D,A,得到四边形ABCD;
(2)求四边形ABCD的面积.
知识点三
特殊位置上点的坐标特征
6.已知点P(m+2,2m-4)在x轴上,则点P的坐标是(
)
A.(4,0)
B.(0,4)
C.(-4,0)
D.(0,-4)
7.若点A(m,n),点B(n,m)表示同一点,则这一点一定在(
)
A.第二、四象限的角平分线上
B.第一、三象限的角平分线上
C.平行于x轴的直线上
D.平行于y轴的直线上
8.若经过点A,B的直线垂直于x轴,且A(x+1,-2)、B(-4,1),则x=_________.
9.已知平面直角坐标系内的点P(3-a,2a+9)到两个坐标轴的距离相等,求点P的坐标.
知识点四
由点的坐标确定点的位置继而确定图形的形状
10.在如图所示的直角坐标系中描出下列各组点,并将各组内的点用线段依次连接起来.
(1)(2,0)、(6,0)、(6,1)、(5,0)、(6,-1)、(6,0);
(2)(2,0)、(5,3)、(4,0);
(3)(2,0)、(5,-3)、(4,0).
观察所得到的图形像什么?如果要将此图形向上平移到x轴上方,那么至少要向上平移几个(整数个)单位长度?
11.在如图所示的平面直角坐标系中,描出点A(-2,1),B(3,1),C(-2,-2),D(3,-2).
(1)顺次连接A、B、C、D四点,构成的图形像什么?
(2)线段AB、CD有什么关系?并说明理由.
知识点五
建立平面直角坐标系,确定点的坐标
12.已知A,B,C,D四位同学的家所在位置如图所示,若以A同学家的位置为坐标原点建立平面直角坐标系,C同学家的坐标为(1,5),则B,D两同学家的坐标分别为(
)
A.(2,3),(3,2)
B.(3,2),(2,3)
C.(2,3),(-3,2)
D.(3,2),(-2,3)
13.如图所示,已知棋子“车”的坐标为(-2,1),棋子“马”的坐标为(3,-1),则棋子“炮”的坐标为(
)
A.(1,1)
B.(2,1)
C.(2,2)
D.(3,1)
14.建立两个适当的平面直角坐标系,并分别表示出边长为8的正方形的顶点的坐标.
巩固提高全练
15.已知点A(6,8),B(1,2a),若直线AB∥x轴,则a的值为(
)
A.4
B.2
C.-4
D.-2
16.如果|3-a|+(b+5)2=0,那么点A(a,b)在(
)
A.第四象限
B.第三象限
C.第二象限
D.第一象限
17.如果P(m+3,2m+4)在y轴上,那么点P的坐标是___________.
18.在平面直角坐标系的第四象限内有一点M,到x轴的距离为4,到y轴的距离为5,则点M的坐标为(
)
A.(4,5)
B.(-5,4)
C.(4,-5)
D.(5,-4)
19.已知a+b>0,ab>0,则在如图所示的平面直角坐标系中,小手盖住的点的坐标可能是(
)
A.(a,b)
B.(-a,b)
C.(-a,-b)
D.(a,-b)
20.小明为画一个零件的轴截面,以该轴截面底边所在的直线为x轴,对称轴为y轴,建立如图所示的平面直角坐标系.若坐标轴的单位长度取1
mm,则图中转折点P的坐标是(
)
A.(5,30)
B.(8,10)
C.(9,10)
D.(10,10)
21.下图是老北京城一些地点的分布示意图.在图中,分别以正东、正北方向为x轴、y轴的正方向建立平面直角坐标系,有如下四个结论:
①当表示天安门的点的坐标为(0,0),表示广安门的点的坐标为(-6,-3)时,表示左安门的点的坐标为(5,-6);
②当表示天安门的点的坐标为(0,0),表示广安门的点的坐标为(-12,-6)时,表示左安门的点的坐标为(10,-12);
③当表示天安门的点的坐标为(1,1),表示广安门的点的坐标为(-11,-5)时,表示左安门的点的坐标为(11,-11);
④当表示天安门的点的坐标为(1.5,1.5),表示广安门的点的坐标为(-16.5,-7.5)时,表示左安门的点的坐标为(16.5,-16.5).
上述结论中,所有正确结论的序号是(
)
A.①②③
B.②③④
C.①④
D.①②③④
22.已知点P(x,y)位于第四象限,并且x≤y+4(x,y为整数),写出一个符合上述条件的点P的坐标__________.
23.以水平数轴的原点O为圆心,过正半轴Ox上的每一刻度点画同心圆,将Ox逆时针依次旋转30°、60°、90°、…、330°得到11条射线,构成如图所示的“圆”坐标系,点A、B的坐标分别表示为(5,0°)、(4,300°),则点C的坐标表示为___________.
24.如图所示,在x轴,y轴上分别截取OA,OB,使OA=OB,再分别以点A,B为圆心,以大于AB长为半径画弧,两弧交于点P.若点P的坐标为(a,2a-3),则a的值为________.
25.如图所示,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次运动到点(2,0),第3次运动到点(3,2),……,按这样的规律运动,第2021次运动后,点P的坐标是____________.
26.先阅读下面一段文字,再回答后面的问题.
已知在平面内两点P1(x1,y1)、P2(x2,y2),这两点间的距离公式为P1P2=,同时,当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2-x1|或|y2-y1|.
(1)已知A(2,4)、B(-3,-8),试求A、B两点间的距离;
(2)已知A、B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为-1,试求A、B两点间的距离;
(3)已知一个三角形各顶点坐标为A(0,6)、B(-3,2)、C(3,2),你能判断此三角形的形状吗?说明理由.
参考答案
1.B
2.D
3.D
4.(1,-3)
5.解析
(1)如图所示.
(2)由图可知,S四边形ABCD=S梯形AB0D+S△COD=×(1+2)×2+×1×2=3+1=4.
6.A
7.B
8.
-5
9.解析
∵点P(3-a,2a+9)到两个坐标轴的距离相等,
∴3-a=2a+9或3-a+2a+9=0,解得a=-2或a=-12.
当a=-2时,3-a=5,2a+9=5,此时,点P的坐标为(5,5);
当a=-12时,3-a=15,2a+9=-15,此时,点P的坐标为(15,-15).
综上所述,点P的坐标为(5,5)或(15,-15).
10.解析
如图所示.
图形像一条金鱼,要将此图形向上平移到x轴上方,那么至少要向上平移4个单位长度.
11.解析
描点如图.
(1)顺次连接A、B、C、D四点,构成的图形像字母“Z”.
(2)AB∥CD,AB=CD.
理由如下:
∵A(-2,1),B(3,1),∴A,B两点的纵坐标相同.
∴AB∥x轴.同理,CD∥x轴.∴AB∥CD.
由A(-2,1),B(3,1),C(-2,-2),D(3,-2)得,AB=5,CD=5,∴AB=CD.
12.D
13.B
14.解析
答案不唯一如图1,以正方形两邻边所在的直线为坐标轴,建立平面直角坐标系,则A(8,0),B(8,8),C(0,8),O(0,0).
如图2,以正方形的两条对称轴所在的直线为坐标轴,建立平面直角坐标系,则A(4,4),B(4,4),C(-4,4),D(-4,-4).
15.A
16.A
17.(0,-2)
18.D
19.B
20.C
21.D
22.(1,-2)(答案不唯一)
23.(3,240°)
24.
3
25.(2021,1)
26.解析
(1)∵A(2,4)、B(-3,-8),
∴AB==13,即A、B两点间的距离是13.
(2)∵A、B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为-1,
∴AB=|-1-5|=6,即A、B两点间的距离是6.
(3)能,△ABC是等腰三角形理由:∵一个三角形各顶点坐标为A(0,6)、B(-3,2)、C(3,2),∴AB=5,BC=6,AC=5,∴AB=AC,∴△ABC是等腰三角形.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
