1.3探索三角形全等的条件SSS 培优训练(Word版含答案)-2021年八年级数学苏科版上册
文档属性
| 名称 | 1.3探索三角形全等的条件SSS 培优训练(Word版含答案)-2021年八年级数学苏科版上册 |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-23 11:25:53 | ||
图片预览



文档简介
苏科版数学八年级培优训练
1.3探索三角形全等的条件SSS
一、选择题
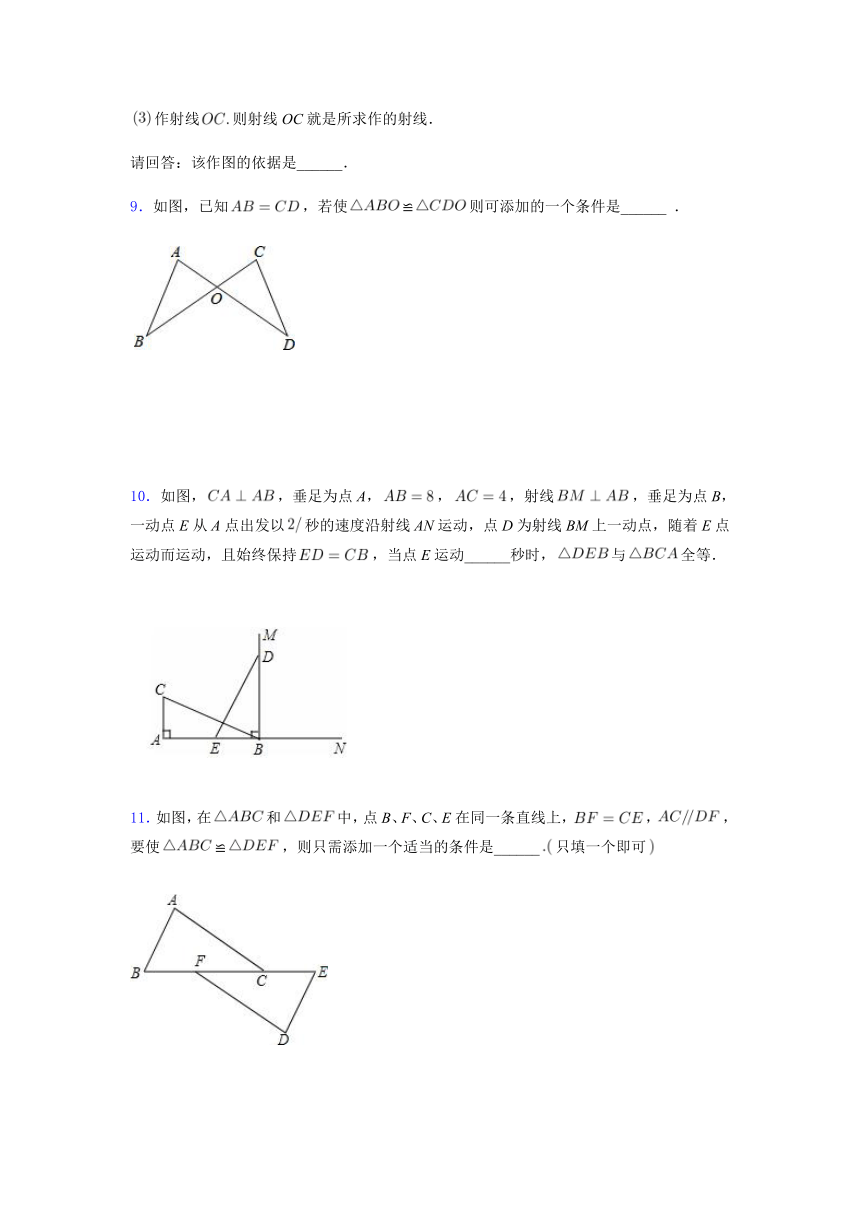
1.如图,已知,再添加一个条件仍不能判定≌的是???
A.
B.
C.
D.
2.如图,点F、C在线段BE上,且,,补充一个条件,不一定使≌成立的是
A.
B.
C.
D.
3.如图,点A,E,F,D在同一直线上,,,,则图中全等三角形共有
A.
1对
B.
2对
C.
3对
D.
4对
4.如图,已知,则不一定能使≌的条件是
A.
B.
C.
D.
5.如图,尺规作图作的平分线的方法如下:以O为圆心,任意长为半径画弧交OA、OB于点C、D,再分别以点C、D为圆心,大于的长为半径画弧,两弧交于点P,作射线由作法得≌从而得两角相等的根据是
A.
SAS
B.
SSS
C.
AAS
D.
ASA
6.如图,点E、F、C、B在同一直线上,,,添加下列一个条件,不能判定≌的条件是
A.
B.
C.
D.
二、填空题
7.两组邻边相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中,,詹姆斯在探究筝形的性质时,得到如下结论:;≌;;四边形ABCD的面积,其中,正确的结论有__________.
8.阅读下面材料:下面是“作角的平分线”的尺规作图过程.
已知:.
求作:射线OC,使它平分.
如图,作法如下:
以点O为圆心,任意长为半径作弧,交OA于E,交OB于D;
分别以点D,E为圆心,以大于的同样长为半径作弧,两弧交于点C;
作射线则射线OC就是所求作的射线.
请回答:该作图的依据是______.
9.如图,已知,若使≌则可添加的一个条件是______
.
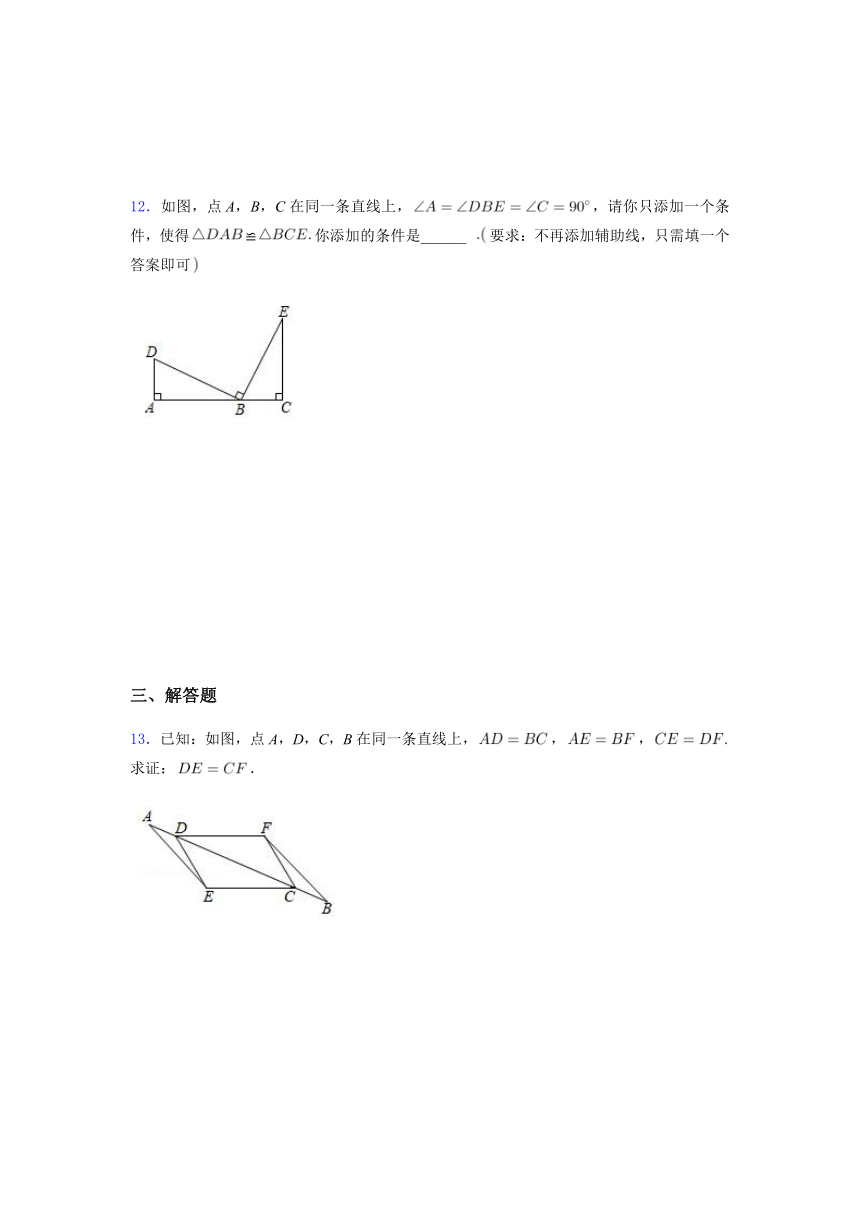
10.如图,,垂足为点A,,,射线,垂足为点B,一动点E从A点出发以秒的速度沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持,当点E运动______秒时,与全等.?
11.如图,在和中,点B、F、C、E在同一条直线上,,,要使≌,则只需添加一个适当的条件是______只填一个即可
12.如图,点A,B,C在同一条直线上,,请你只添加一个条件,使得≌你添加的条件是______
要求:不再添加辅助线,只需填一个答案即可
三、解答题
13.已知:如图,点A,D,C,B在同一条直线上,,,求证:.
14.点F、B、E、C在同一直线上,并且,能否由上面的已知条件证明≌?如果能,请给出证明;如果不能,请从下列三个条件中选择一个合适的条件添加到已知条件中,使≌,并给出证明.提供的三个条件是:;;.
15.在数学活动课上,李老师让同学们试着用角尺平分如图所示有两组同学设计了如下方案.
方案:将角尺的直角顶点P介于射线OA,OB之间,移动角尺使角尺两边相同的刻度位于OA,OB上,且交点分别为M,N,即,过角尺顶点P的射线OP就是的平分线.
方案:在边OA,OB上分别截取,将角尺的直角顶点P介于射线OA,OB之间,移动角尺使角尺两边相同的刻度与点M,N重合,即,过角尺顶点P的射线OP就是的平分线.
方案与方案是否可行?若可行,请证明;若不可行,请说明理由.
16.如图,已知,,AC与BD相交于E,F是BC的中点,求证:.
17.阅读材料,解答问题
数学课上,同学们兴致勃勃地探讨着利用不同画图工具画角的平分线的方法.
小惠说:如图1,我用相同的两块含?角的直角三角板可以画角的平分线.画法如下:
在的两边上分别取点M,N,使;
把直角三角板按如图所示的位置放置,两斜边交于点P.
射线OP是的平分线.
小旭说:我只用刻度尺就可以画角平分线.
请你也参与探讨,解决以下问题:
小惠的做法正确吗?说明理由;
请你和小旭一样,只用刻度尺画出图2中的平分线,并简述画图的过程.
苏科版数学八年级培优训练(教师卷)
1.3探索三角形全等的条件SSS
一、选择题
1.如图,已知,再添加一个条件仍不能判定≌的是???
A.
B.
C.
D.
答案:D
解析:【分析】
本题重点考查了三角形全等的判定定理,普通两个三角形全等共有四个定理,即AAS、ASA、SAS、SSS,直角三角形可用HL定理,但AAA、SSA,无法证明三角形全等,本题是一道较为简单的题目.
根据全等三角形的判定定理分别判定即可.
【解答】
解:A、根据HL可判定≌,故本选项不符合题意;
B、根据SAS可判定≌,故本选项不符合题意;
C、根据SSS可判定≌,故本选项不符合题意;
D、根据SSA不能判定≌,故本选项符合题意;
故选:D.
2.如图,点F、C在线段BE上,且,,补充一个条件,不一定使≌成立的是
A.
B.
C.
D.
答案:A
解析:【分析】
本题考查三角形全等的判定方法.解题关键是掌握全等三角形的判定方法,判定两个三角形全等的一般方法有:SSS,SAS,ASA,AAS,注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.解题时,根据题中的已知条件,,再结合题目中所给选项中的条件,利用全等三角形的判定定理进行分析即可.
【解答】
解:在和中,,
.
A.当时,由已知条件,,可知SSA不能判定两个三角形全等,故此选项符合题意;
B.当时,由已知条件,,可知SAS能判定两个三角形全等,故此选项不符合题意;
C.当时,由已知条件,,可知AAS能判定两个三角形全等,故此选项不符合题意;
D.当时,由已知条件,,可知ASA能判定两个三角形全等,故此选项不符合题意.
故选A.
3.如图,点A,E,F,D在同一直线上,,,,则图中全等三角形共有
A.
1对
B.
2对
C.
3对
D.
4对
答案:C
解析:【分析】
本题考查了全等三角形的判定定理的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,求出,,根据SAS推出≌,≌,求出,,推出,根据SAS推出≌即可.
【解答】
解:,
,
,
,
,
在和中,,
≌,
在和中,,
≌,
,,
,
在和中,,
≌,即全等三角形有3对.
故选C.
4.如图,已知,则不一定能使≌的条件是
A.
B.
C.
D.
答案:A
解析:解:A、,BC为公共边,若,则不一定能使≌,故本选项正确;
B、,BC为公共边,若,则≌,故本选项错误;
C、,BC为公共边,若,则≌,故本选项错误;
D、,BC为公共边,若,则≌,故本选项错误;
故选:A.
利用全等三角形判定定理ASA,SAS,AAS对各个选项逐一分析即可得出答案.
本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
5.如图,尺规作图作的平分线的方法如下:以O为圆心,任意长为半径画弧交OA、OB于点C、D,再分别以点C、D为圆心,大于的长为半径画弧,两弧交于点P,作射线由作法得≌从而得两角相等的根据是
A.
SAS
B.
SSS
C.
AAS
D.
ASA
答案:B
解析:解:以O为圆心,任意长为半径画弧交OA,OB于C,D,即;
以点C,D为圆心,以大于长为半径画弧,两弧交于点P,即;
在和中
,
≌.
故选:B.
认真阅读作法,从角平分线的作法得出与的两边分别相等,加上公共边相等,于是两个三角形符合SSS判定方法要求的条件,答案可得.
本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
6.如图,点E、F、C、B在同一直线上,,,添加下列一个条件,不能判定≌的条件是
A.
B.
C.
D.
答案:A
解析:解:A、添加不能判定≌,故本选项符合题意;
B、添加可用SAS进行判定,故本选项不符合题意;
C、添加然后可用ASA进行判定,故本选项不符合题意;
D、添加可用AAS进行判定,故本选项不符合题意;
故选:A.
分别判断选项所添加的条件,根据三角形的判定定理:SSS、SAS、AAS进行判断即可.
本题主要考查对全等三角形的判定,平行线的性质等知识点的理解和掌握,熟练地运用全等三角形的判定定理进行证明是解此题的关键,是一个开放型的题目,比较典型.
二、填空题
7.两组邻边相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中,,詹姆斯在探究筝形的性质时,得到如下结论:;≌;;四边形ABCD的面积,其中,正确的结论有__________.
答案:
解析:【分析】
此题考查全等三角形的判定和性质,关键是根据SSS证明与全等和利用SAS证明与全等.先证明与全等,再证明与全等即可判断.
【解答】
解:在与中,
,
≌,
故正确;
,
在与中,
,
≌,
,,
,
故正确.
四边形的面积,
故正确.
故答案为.
8.阅读下面材料:下面是“作角的平分线”的尺规作图过程.
已知:.
求作:射线OC,使它平分.
如图,作法如下:
以点O为圆心,任意长为半径作弧,交OA于E,交OB于D;
分别以点D,E为圆心,以大于的同样长为半径作弧,两弧交于点C;
作射线则射线OC就是所求作的射线.
请回答:该作图的依据是______.
答案:SSS
解析:解:连接EC,DC,
由作图可得,,
在和中,
≌,
,
平分.
故答案为:SSS.
【分析】由作图可得,,根据三角形全等的判定方法“SSS”解答.
本题考查了全等三角形的应用,以及基本作图,熟练掌握三角形全等的判定方法并读懂题目信息是解题的关键.
9.如图,已知,若使≌则可添加的一个条件是______
.
答案:
解析:解:,
理由是:在和中
≌,
故答案为:.
此题是一道开放型的题目,答案不唯一,只要符合全等三角形的判定定理就行.
本题考查了全等三角形的判定定理的应用,能熟记全等三角形的判定定理是解此题的关键,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.
10.如图,,垂足为点A,,,射线,垂足为点B,一动点E从A点出发以秒的速度沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持,当点E运动______秒时,与全等.?
答案:0,2,6,8
解析:【分析】
本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.先分两种情况:当E在线段AB上时,当E在BN上,再分别分成两种情况,进行计算即可.
【解答】
解:当E在线段AB上,时,≌,
,
,
,
点E的运动时间为秒;
当E在BN上,时,
,
,
,
点E的运动时间为秒;
当E在线段AB上,时,≌,
这时E在A点未动,因此时间为0秒;
当E在BN上,时,≌,
,
点E的运动时间为秒,
故答案为0,2,6,8.
11.如图,在和中,点B、F、C、E在同一条直线上,,,要使≌,则只需添加一个适当的条件是______只填一个即可
答案:
解析:解:,
理由是:,
,
,
,
,
在和中,
≌,
故答案为:答案不唯一
求出,,根据SAS推出两三角形全等即可.
本题考查了全等三角形的判定的应用,关键是注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,答案不唯一.
12.如图,点A,B,C在同一条直线上,,请你只添加一个条件,使得≌你添加的条件是______
要求:不再添加辅助线,只需填一个答案即可
答案:答案不唯一
解析:解:添加的条件是,
理由是:,
,,
,
在和中,
,
≌,
故答案为:答案不唯一.
此题是一道开放型的题目,答案不唯一,只要符合全等三角形的判定定理即可.
本题考查了全等三角形的判定定理,能熟记全等三角形的判定定理是解此题的关键,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,两直角三角形全等还有HL.
三、解答题
13.已知:如图,点A,D,C,B在同一条直线上,,,求证:.
答案:证明:,
,
,
在和中,
,
≌,
,
在和中,
,
≌,
.
解析:证明≌,由全等三角形的性质得出,根据SAS证明≌,则可得出.
本题考查了全等三角形的判定及性质,熟练掌握全等三角形的判定方法是解题的关键.
14.点F、B、E、C在同一直线上,并且,能否由上面的已知条件证明≌?如果能,请给出证明;如果不能,请从下列三个条件中选择一个合适的条件添加到已知条件中,使≌,并给出证明.提供的三个条件是:;;.
答案:解:不能;
选择条件:;
,
,
即,
在和中,
≌.
解析:此题主要考查了全等三角形的判定,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、?注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.由可得,再有条件不能证明≌;可以加上条件,利用SAS定理可以判定≌.
15.在数学活动课上,李老师让同学们试着用角尺平分如图所示有两组同学设计了如下方案.
方案:将角尺的直角顶点P介于射线OA,OB之间,移动角尺使角尺两边相同的刻度位于OA,OB上,且交点分别为M,N,即,过角尺顶点P的射线OP就是的平分线.
方案:在边OA,OB上分别截取,将角尺的直角顶点P介于射线OA,OB之间,移动角尺使角尺两边相同的刻度与点M,N重合,即,过角尺顶点P的射线OP就是的平分线.
方案与方案是否可行?若可行,请证明;若不可行,请说明理由.
答案:解:方案不可行;理由如下:
只有,,不能判断≌,
不能判定OP就是的平分线;
方案可行;理由如下:
在和中,,
≌,
.
就是的平分线.
解析:只有,,不能判断≌,得出方案不可行;
由SSS证得≌,得出得出方案可行.
本题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定是解题的关键.
16.如图,已知,,AC与BD相交于E,F是BC的中点,求证:.
答案:证明:在和中,
,
≌,
,
是BC的中点,
,
在和中,
,
≌,
.
解析:先利用AAS证明≌,再利用SSS证明≌即可.
本题主要考查了全等三角形的判定与性质,解题的关键是熟练掌握利用AAS和SSS证明三角形全等,此题难度不大.
17.阅读材料,解答问题
数学课上,同学们兴致勃勃地探讨着利用不同画图工具画角的平分线的方法.
小惠说:如图1,我用相同的两块含?角的直角三角板可以画角的平分线.画法如下:
在的两边上分别取点M,N,使;
把直角三角板按如图所示的位置放置,两斜边交于点P.
射线OP是的平分线.
小旭说:我只用刻度尺就可以画角平分线.
请你也参与探讨,解决以下问题:
小惠的做法正确吗?说明理由;
请你和小旭一样,只用刻度尺画出图2中的平分线,并简述画图的过程.
答案:解:小惠的做法正确.
理由如下:
如图1,过O点作于C,于D.
,
由题意,,
,.
.
在和中,
,
≌,
,,
于C,于D,
点O在的平分线上,
,
,
,
即?射线OP是的平分线;
如图2,射线RX是的平分线,
作图过程是:用刻度尺作,,
连接TW,UV交于点X,
射线RX即为所求的平分线.
解析:过O点作于C,于D,求出≌,根据全等三角形的性质得出,,根据角平分线性质求出根据三角形内角和定理求出即可;
根据全等三角形的判定定理SSS,用刻度尺作出即可.
本题考查了角平分线定义和全等三角形的判定和性质的应用,主要考查学生的理解能力和动手操作能力,题目比较好,难度适中.
1.3探索三角形全等的条件SSS
一、选择题
1.如图,已知,再添加一个条件仍不能判定≌的是???
A.
B.
C.
D.
2.如图,点F、C在线段BE上,且,,补充一个条件,不一定使≌成立的是
A.
B.
C.
D.
3.如图,点A,E,F,D在同一直线上,,,,则图中全等三角形共有
A.
1对
B.
2对
C.
3对
D.
4对
4.如图,已知,则不一定能使≌的条件是
A.
B.
C.
D.
5.如图,尺规作图作的平分线的方法如下:以O为圆心,任意长为半径画弧交OA、OB于点C、D,再分别以点C、D为圆心,大于的长为半径画弧,两弧交于点P,作射线由作法得≌从而得两角相等的根据是
A.
SAS
B.
SSS
C.
AAS
D.
ASA
6.如图,点E、F、C、B在同一直线上,,,添加下列一个条件,不能判定≌的条件是
A.
B.
C.
D.
二、填空题
7.两组邻边相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中,,詹姆斯在探究筝形的性质时,得到如下结论:;≌;;四边形ABCD的面积,其中,正确的结论有__________.
8.阅读下面材料:下面是“作角的平分线”的尺规作图过程.
已知:.
求作:射线OC,使它平分.
如图,作法如下:
以点O为圆心,任意长为半径作弧,交OA于E,交OB于D;
分别以点D,E为圆心,以大于的同样长为半径作弧,两弧交于点C;
作射线则射线OC就是所求作的射线.
请回答:该作图的依据是______.
9.如图,已知,若使≌则可添加的一个条件是______
.
10.如图,,垂足为点A,,,射线,垂足为点B,一动点E从A点出发以秒的速度沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持,当点E运动______秒时,与全等.?
11.如图,在和中,点B、F、C、E在同一条直线上,,,要使≌,则只需添加一个适当的条件是______只填一个即可
12.如图,点A,B,C在同一条直线上,,请你只添加一个条件,使得≌你添加的条件是______
要求:不再添加辅助线,只需填一个答案即可
三、解答题
13.已知:如图,点A,D,C,B在同一条直线上,,,求证:.
14.点F、B、E、C在同一直线上,并且,能否由上面的已知条件证明≌?如果能,请给出证明;如果不能,请从下列三个条件中选择一个合适的条件添加到已知条件中,使≌,并给出证明.提供的三个条件是:;;.
15.在数学活动课上,李老师让同学们试着用角尺平分如图所示有两组同学设计了如下方案.
方案:将角尺的直角顶点P介于射线OA,OB之间,移动角尺使角尺两边相同的刻度位于OA,OB上,且交点分别为M,N,即,过角尺顶点P的射线OP就是的平分线.
方案:在边OA,OB上分别截取,将角尺的直角顶点P介于射线OA,OB之间,移动角尺使角尺两边相同的刻度与点M,N重合,即,过角尺顶点P的射线OP就是的平分线.
方案与方案是否可行?若可行,请证明;若不可行,请说明理由.
16.如图,已知,,AC与BD相交于E,F是BC的中点,求证:.
17.阅读材料,解答问题
数学课上,同学们兴致勃勃地探讨着利用不同画图工具画角的平分线的方法.
小惠说:如图1,我用相同的两块含?角的直角三角板可以画角的平分线.画法如下:
在的两边上分别取点M,N,使;
把直角三角板按如图所示的位置放置,两斜边交于点P.
射线OP是的平分线.
小旭说:我只用刻度尺就可以画角平分线.
请你也参与探讨,解决以下问题:
小惠的做法正确吗?说明理由;
请你和小旭一样,只用刻度尺画出图2中的平分线,并简述画图的过程.
苏科版数学八年级培优训练(教师卷)
1.3探索三角形全等的条件SSS
一、选择题
1.如图,已知,再添加一个条件仍不能判定≌的是???
A.
B.
C.
D.
答案:D
解析:【分析】
本题重点考查了三角形全等的判定定理,普通两个三角形全等共有四个定理,即AAS、ASA、SAS、SSS,直角三角形可用HL定理,但AAA、SSA,无法证明三角形全等,本题是一道较为简单的题目.
根据全等三角形的判定定理分别判定即可.
【解答】
解:A、根据HL可判定≌,故本选项不符合题意;
B、根据SAS可判定≌,故本选项不符合题意;
C、根据SSS可判定≌,故本选项不符合题意;
D、根据SSA不能判定≌,故本选项符合题意;
故选:D.
2.如图,点F、C在线段BE上,且,,补充一个条件,不一定使≌成立的是
A.
B.
C.
D.
答案:A
解析:【分析】
本题考查三角形全等的判定方法.解题关键是掌握全等三角形的判定方法,判定两个三角形全等的一般方法有:SSS,SAS,ASA,AAS,注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.解题时,根据题中的已知条件,,再结合题目中所给选项中的条件,利用全等三角形的判定定理进行分析即可.
【解答】
解:在和中,,
.
A.当时,由已知条件,,可知SSA不能判定两个三角形全等,故此选项符合题意;
B.当时,由已知条件,,可知SAS能判定两个三角形全等,故此选项不符合题意;
C.当时,由已知条件,,可知AAS能判定两个三角形全等,故此选项不符合题意;
D.当时,由已知条件,,可知ASA能判定两个三角形全等,故此选项不符合题意.
故选A.
3.如图,点A,E,F,D在同一直线上,,,,则图中全等三角形共有
A.
1对
B.
2对
C.
3对
D.
4对
答案:C
解析:【分析】
本题考查了全等三角形的判定定理的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,求出,,根据SAS推出≌,≌,求出,,推出,根据SAS推出≌即可.
【解答】
解:,
,
,
,
,
在和中,,
≌,
在和中,,
≌,
,,
,
在和中,,
≌,即全等三角形有3对.
故选C.
4.如图,已知,则不一定能使≌的条件是
A.
B.
C.
D.
答案:A
解析:解:A、,BC为公共边,若,则不一定能使≌,故本选项正确;
B、,BC为公共边,若,则≌,故本选项错误;
C、,BC为公共边,若,则≌,故本选项错误;
D、,BC为公共边,若,则≌,故本选项错误;
故选:A.
利用全等三角形判定定理ASA,SAS,AAS对各个选项逐一分析即可得出答案.
本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
5.如图,尺规作图作的平分线的方法如下:以O为圆心,任意长为半径画弧交OA、OB于点C、D,再分别以点C、D为圆心,大于的长为半径画弧,两弧交于点P,作射线由作法得≌从而得两角相等的根据是
A.
SAS
B.
SSS
C.
AAS
D.
ASA
答案:B
解析:解:以O为圆心,任意长为半径画弧交OA,OB于C,D,即;
以点C,D为圆心,以大于长为半径画弧,两弧交于点P,即;
在和中
,
≌.
故选:B.
认真阅读作法,从角平分线的作法得出与的两边分别相等,加上公共边相等,于是两个三角形符合SSS判定方法要求的条件,答案可得.
本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
6.如图,点E、F、C、B在同一直线上,,,添加下列一个条件,不能判定≌的条件是
A.
B.
C.
D.
答案:A
解析:解:A、添加不能判定≌,故本选项符合题意;
B、添加可用SAS进行判定,故本选项不符合题意;
C、添加然后可用ASA进行判定,故本选项不符合题意;
D、添加可用AAS进行判定,故本选项不符合题意;
故选:A.
分别判断选项所添加的条件,根据三角形的判定定理:SSS、SAS、AAS进行判断即可.
本题主要考查对全等三角形的判定,平行线的性质等知识点的理解和掌握,熟练地运用全等三角形的判定定理进行证明是解此题的关键,是一个开放型的题目,比较典型.
二、填空题
7.两组邻边相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中,,詹姆斯在探究筝形的性质时,得到如下结论:;≌;;四边形ABCD的面积,其中,正确的结论有__________.
答案:
解析:【分析】
此题考查全等三角形的判定和性质,关键是根据SSS证明与全等和利用SAS证明与全等.先证明与全等,再证明与全等即可判断.
【解答】
解:在与中,
,
≌,
故正确;
,
在与中,
,
≌,
,,
,
故正确.
四边形的面积,
故正确.
故答案为.
8.阅读下面材料:下面是“作角的平分线”的尺规作图过程.
已知:.
求作:射线OC,使它平分.
如图,作法如下:
以点O为圆心,任意长为半径作弧,交OA于E,交OB于D;
分别以点D,E为圆心,以大于的同样长为半径作弧,两弧交于点C;
作射线则射线OC就是所求作的射线.
请回答:该作图的依据是______.
答案:SSS
解析:解:连接EC,DC,
由作图可得,,
在和中,
≌,
,
平分.
故答案为:SSS.
【分析】由作图可得,,根据三角形全等的判定方法“SSS”解答.
本题考查了全等三角形的应用,以及基本作图,熟练掌握三角形全等的判定方法并读懂题目信息是解题的关键.
9.如图,已知,若使≌则可添加的一个条件是______
.
答案:
解析:解:,
理由是:在和中
≌,
故答案为:.
此题是一道开放型的题目,答案不唯一,只要符合全等三角形的判定定理就行.
本题考查了全等三角形的判定定理的应用,能熟记全等三角形的判定定理是解此题的关键,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS.
10.如图,,垂足为点A,,,射线,垂足为点B,一动点E从A点出发以秒的速度沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持,当点E运动______秒时,与全等.?
答案:0,2,6,8
解析:【分析】
本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.先分两种情况:当E在线段AB上时,当E在BN上,再分别分成两种情况,进行计算即可.
【解答】
解:当E在线段AB上,时,≌,
,
,
,
点E的运动时间为秒;
当E在BN上,时,
,
,
,
点E的运动时间为秒;
当E在线段AB上,时,≌,
这时E在A点未动,因此时间为0秒;
当E在BN上,时,≌,
,
点E的运动时间为秒,
故答案为0,2,6,8.
11.如图,在和中,点B、F、C、E在同一条直线上,,,要使≌,则只需添加一个适当的条件是______只填一个即可
答案:
解析:解:,
理由是:,
,
,
,
,
在和中,
≌,
故答案为:答案不唯一
求出,,根据SAS推出两三角形全等即可.
本题考查了全等三角形的判定的应用,关键是注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,答案不唯一.
12.如图,点A,B,C在同一条直线上,,请你只添加一个条件,使得≌你添加的条件是______
要求:不再添加辅助线,只需填一个答案即可
答案:答案不唯一
解析:解:添加的条件是,
理由是:,
,,
,
在和中,
,
≌,
故答案为:答案不唯一.
此题是一道开放型的题目,答案不唯一,只要符合全等三角形的判定定理即可.
本题考查了全等三角形的判定定理,能熟记全等三角形的判定定理是解此题的关键,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,两直角三角形全等还有HL.
三、解答题
13.已知:如图,点A,D,C,B在同一条直线上,,,求证:.
答案:证明:,
,
,
在和中,
,
≌,
,
在和中,
,
≌,
.
解析:证明≌,由全等三角形的性质得出,根据SAS证明≌,则可得出.
本题考查了全等三角形的判定及性质,熟练掌握全等三角形的判定方法是解题的关键.
14.点F、B、E、C在同一直线上,并且,能否由上面的已知条件证明≌?如果能,请给出证明;如果不能,请从下列三个条件中选择一个合适的条件添加到已知条件中,使≌,并给出证明.提供的三个条件是:;;.
答案:解:不能;
选择条件:;
,
,
即,
在和中,
≌.
解析:此题主要考查了全等三角形的判定,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、?注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.由可得,再有条件不能证明≌;可以加上条件,利用SAS定理可以判定≌.
15.在数学活动课上,李老师让同学们试着用角尺平分如图所示有两组同学设计了如下方案.
方案:将角尺的直角顶点P介于射线OA,OB之间,移动角尺使角尺两边相同的刻度位于OA,OB上,且交点分别为M,N,即,过角尺顶点P的射线OP就是的平分线.
方案:在边OA,OB上分别截取,将角尺的直角顶点P介于射线OA,OB之间,移动角尺使角尺两边相同的刻度与点M,N重合,即,过角尺顶点P的射线OP就是的平分线.
方案与方案是否可行?若可行,请证明;若不可行,请说明理由.
答案:解:方案不可行;理由如下:
只有,,不能判断≌,
不能判定OP就是的平分线;
方案可行;理由如下:
在和中,,
≌,
.
就是的平分线.
解析:只有,,不能判断≌,得出方案不可行;
由SSS证得≌,得出得出方案可行.
本题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定是解题的关键.
16.如图,已知,,AC与BD相交于E,F是BC的中点,求证:.
答案:证明:在和中,
,
≌,
,
是BC的中点,
,
在和中,
,
≌,
.
解析:先利用AAS证明≌,再利用SSS证明≌即可.
本题主要考查了全等三角形的判定与性质,解题的关键是熟练掌握利用AAS和SSS证明三角形全等,此题难度不大.
17.阅读材料,解答问题
数学课上,同学们兴致勃勃地探讨着利用不同画图工具画角的平分线的方法.
小惠说:如图1,我用相同的两块含?角的直角三角板可以画角的平分线.画法如下:
在的两边上分别取点M,N,使;
把直角三角板按如图所示的位置放置,两斜边交于点P.
射线OP是的平分线.
小旭说:我只用刻度尺就可以画角平分线.
请你也参与探讨,解决以下问题:
小惠的做法正确吗?说明理由;
请你和小旭一样,只用刻度尺画出图2中的平分线,并简述画图的过程.
答案:解:小惠的做法正确.
理由如下:
如图1,过O点作于C,于D.
,
由题意,,
,.
.
在和中,
,
≌,
,,
于C,于D,
点O在的平分线上,
,
,
,
即?射线OP是的平分线;
如图2,射线RX是的平分线,
作图过程是:用刻度尺作,,
连接TW,UV交于点X,
射线RX即为所求的平分线.
解析:过O点作于C,于D,求出≌,根据全等三角形的性质得出,,根据角平分线性质求出根据三角形内角和定理求出即可;
根据全等三角形的判定定理SSS,用刻度尺作出即可.
本题考查了角平分线定义和全等三角形的判定和性质的应用,主要考查学生的理解能力和动手操作能力,题目比较好,难度适中.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
