1.3探索三角形全等的条件SAS 培优训练(Word版含答案)-2021年八年级数学苏科版上册
文档属性
| 名称 | 1.3探索三角形全等的条件SAS 培优训练(Word版含答案)-2021年八年级数学苏科版上册 |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-23 12:51:48 | ||
图片预览

文档简介
苏科版数学八年级培优训练
1.3探索三角形全等的条件SAS
一、选择题
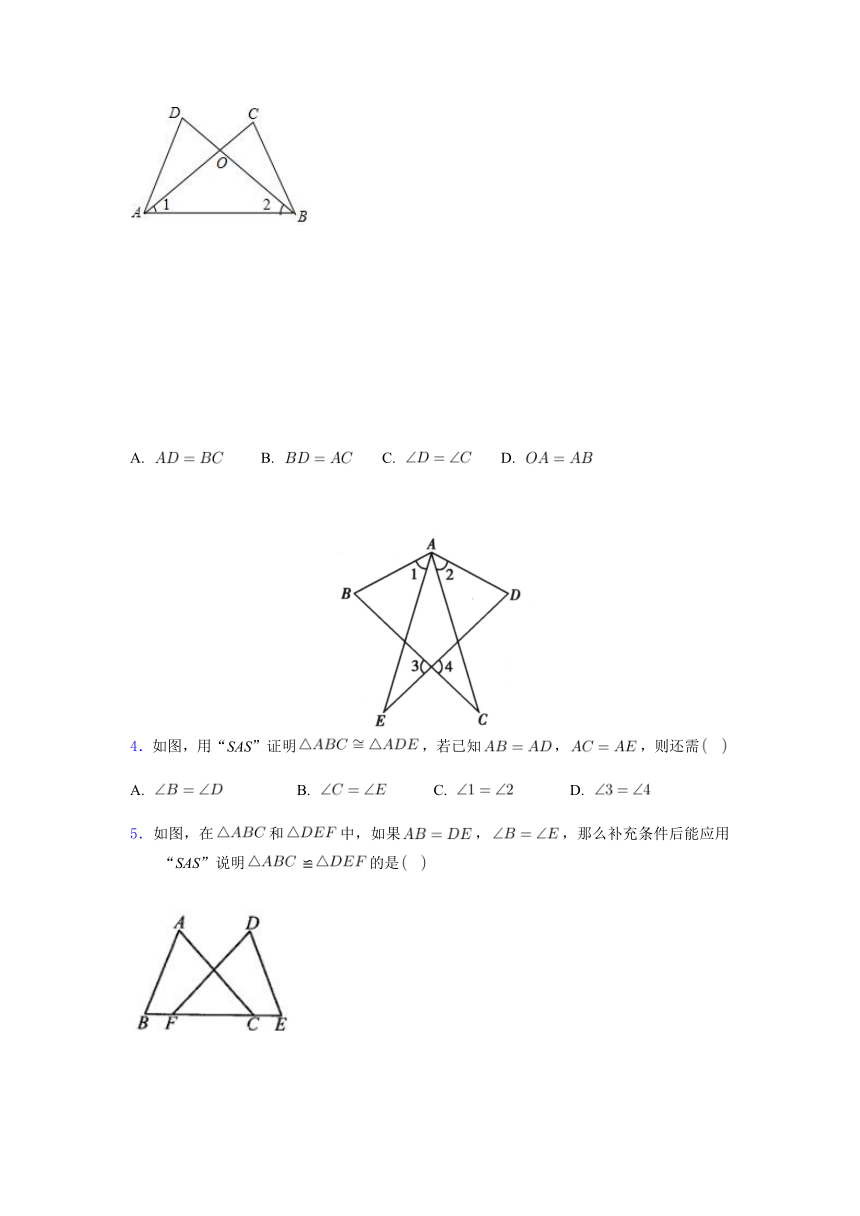
1.如图,已知,要使≌,只需要添加一个条件是
A.
B.
C.
D.
2.如图,已知,,,由这三个条件,就可得出≌,依据的判定方法是
A.
边边边
B.
边角边
C.
角边角
D.
角角边
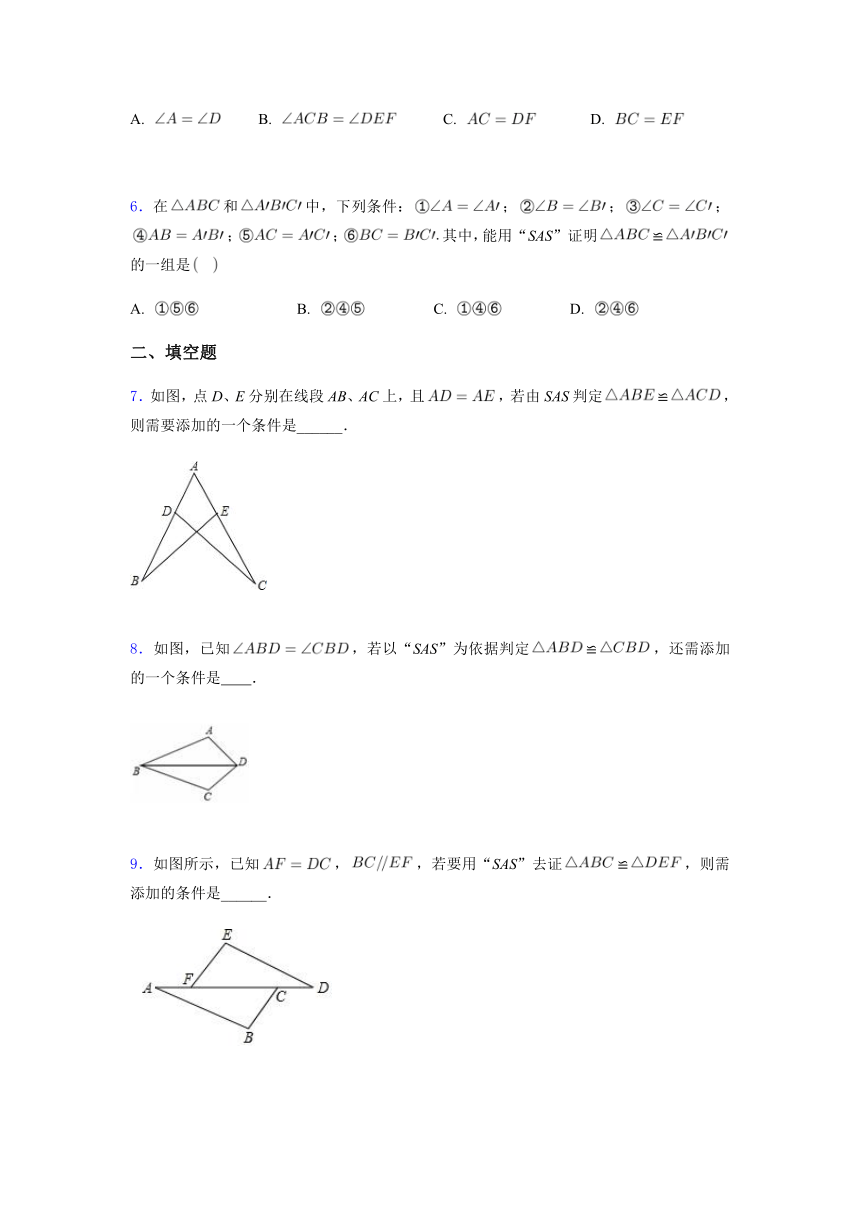
3.如图,AC、BD相交于点O,,若用“SAS”说明≌,则还需要加上条件
A.
B.
C.
D.
4.如图,用“SAS”证明,若已知,,则还需
A.
B.
C.
D.
5.如图,在和中,如果,,那么补充条件后能应用“SAS”说明≌的是
A.
B.
C.
D.
6.在和中,下列条件:;;;;;其中,能用“SAS”证明≌的一组是
A.
B.
C.
D.
二、填空题
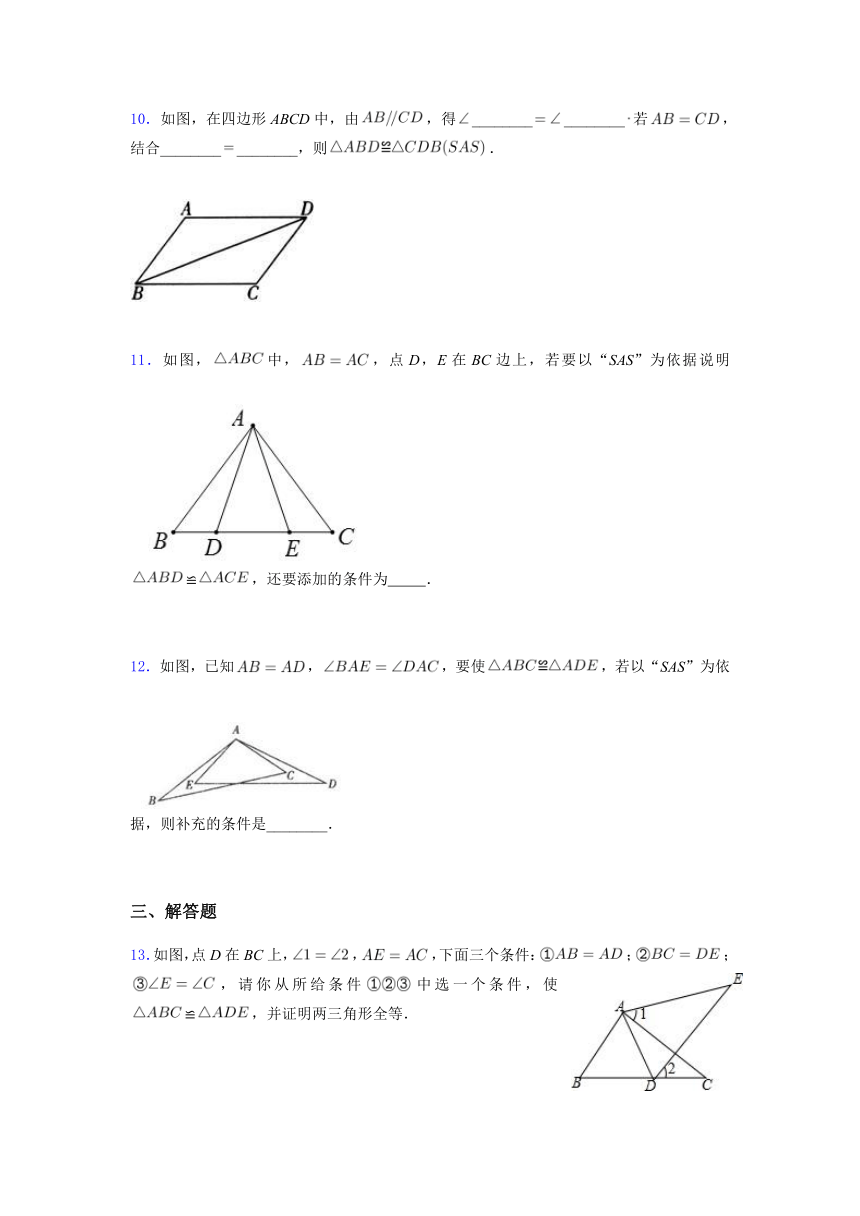
7.如图,点D、E分别在线段AB、AC上,且,若由SAS判定≌,则需要添加的一个条件是______.
8.如图,已知,若以“SAS”为依据判定≌,还需添加的一个条件是?
?
??.
9.如图所示,已知,,若要用“SAS”去证≌,则需添加的条件是______.
10.如图,在四边形ABCD中,由,得________________若,结合________________,则.
11.如图,中,,点D,E在BC边上,若要以“SAS”为依据说明≌,还要添加的条件为??????????.
12.如图,已知,,要使,若以“SAS”为依据,则补充的条件是________.
三、解答题
13.如图,点D在BC上,,,下面三个条件:;;,请你从所给条件中选一个条件,使≌,并证明两三角形全等.
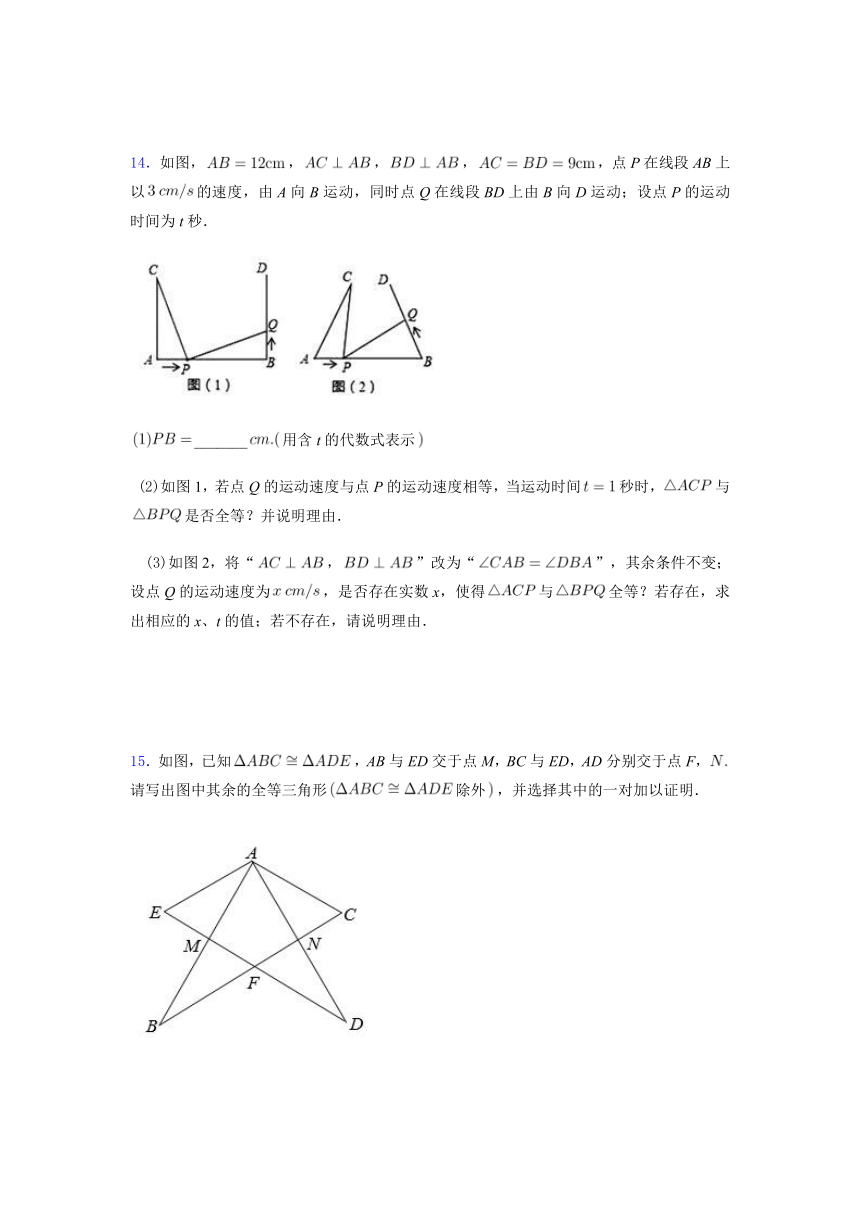
14.如图,,,,,点P在线段AB上以的速度,由A向B运动,同时点Q在线段BD上由B向D运动;设点P的运动时间为t秒.
_______用含t的代数式表示
(2)如图1,若点Q的运动速度与点P的运动速度相等,当运动时间秒时,与是否全等?并说明理由.
(3)如图2,将“,”改为“”,其余条件不变;设点Q的运动速度为,是否存在实数x,使得与全等?若存在,求出相应的x、t的值;若不存在,请说明理由.
15.如图,已知,AB与ED交于点M,BC与ED,AD分别交于点F,请写出图中其余的全等三角形除外,并选择其中的一对加以证明.
16.【问题情境】
课外兴趣小组活动时,老师提出了如下问题:
如图,中,若,,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD至点E,使,连接请根据小明的方法思考:
Ⅰ由已知和作图能得到≌,依据是______.
A.SSS????????????
Ⅱ由“三角形的三边关系”可求得AD的取值范围是______.
解后反思:题目中出现“中点”、“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形之中.
【初步运用】
如图,AD是的中线,BE交AC于E,交AD于F,且若,,求线段BF的长.
17.探究问题:如图1,在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足,连接EF,求证:.
方法感悟:延长CB至G,使,
可证≌,,
,
又,
?,即,
又,,≌,
,故DE;
方法迁移:如图2将沿斜边翻折得到,点E、F分别为DC、BC上的点,且试猜想DE、BF、EF之间有何数量关系,并证明你的猜想.
形成模型:如图3,在四边形ABCD中,,E、F分别为DC、BC上的点,,,可得.
模型应用:如图4,在某次军事演习中,舰艇甲在指挥中心处北偏西的A处,舰艇乙在指挥中心南偏东的B处,并且两舰艇到指挥中心的距离相等。接到行动指令后,舰艇甲向正东方向以60海里小时的速度前进,舰艇乙沿北偏东的方向以80海里小时的速度前进,小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间夹角为,试求此时两舰艇之间的距离若能得到的模型,可直接应用模型解题的结论,不需再次证明全等.
18.在解决线段数量关系问题中,如果条件中有角平分线,经常采用下面构造全等三角形的解决思路.
如:在图1中,若C是的平分线OP上一点,点A在OM上,此时,在ON截取,连接BC,根据三角形全等的判定,容易构造出全等三角形和,参考上面的方法,解答下列问题:
如图2,在非等边中,,AD、CE分别是、的平分线,且AD、CE交于点求证:.
苏科版数学八年级培优训练(教师卷)
1.3探索三角形全等的条件SAS
一、选择题
1.如图,已知,要使≌,只需要添加一个条件是
A.
B.
C.
D.
答案:D
解析:解:A、根据,和不能推出≌,故本选项不符合题意;
B、根据,和不能推出≌,故本选项不符合题意;
C、根据,和不能推出≌,故本选项不符合题意;
D、根据,,能推出≌,故本选项符合题意;
故选:D.
根据全等三角形的判定定理逐个判断即可.
本题考查了全等三角形的判定定理,能熟记全等三角形的判定定理的内容是解此题的关键,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS等.
2.如图,已知,,,由这三个条件,就可得出≌,依据的判定方法是
A.
边边边
B.
边角边
C.
角边角
D.
角角边
答案:B
解析:解:,
,
,
在和中,
,
≌,
故选:B.
根据SAS证明三角形全等即可解决问题.
本题考查全等三角形的判定,解题的关键是熟练掌握全等三角形的判定方法,属于中考常考题型.
3.如图,AC、BD相交于点O,,若用“SAS”说明≌,则还需要加上条件
A.
B.
C.
D.
答案:B
解析:【分析】
本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.已有条件,,若用“SAS”说明≌必须添加边相等,根据判定方法可得应添加.
【解答】
解:还需要加上条件,
在和中,
≌,
故选:B.
4.如图,用“SAS”证明,若已知,,则还需
A.
B.
C.
D.
答案:C
解析:【分析】
本题考查全等三角形的判定,根据题目中给出的条件,,要用“SAS”还缺少条件是夹角:,筛选答案可选出C.
【解答】
解:已知两边分别相等,若其夹角相等,则符合“SAS”,
由得,
即,
故选C.
5.如图,在和中,如果,,那么补充条件后能应用“SAS”说明≌的是
A.
B.
C.
D.
答案:D
解析:【分析】
本题考查了三角形全等的条件,判定三角形全等一定要结合图形上的位置关系,从而选择方法.应用从的两边是AB、BC,的两边是DE、EF分析,找到需要相等的两边.
【解答】
解:两边和它们的夹角对应相等的两个三角形全等.
的两边是AB、BC,的两边是DE、EF,故BC即可.
故选D.
6.在和中,下列条件:;;;;;其中,能用“SAS”证明≌的一组是
A.
B.
C.
D.
答案:D
解析:【试题解析】
【分析】
此题主要考查了全等三角形的判定,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.由于全等三角形的六个元素,其中找到能用“SAS”证明≌的元素,由此即可求解.?
【解答】
解:根据题意,其中能用“SAS”证明≌的,和,
故选D.
二、填空题
7.如图,点D、E分别在线段AB、AC上,且,若由SAS判定≌,则需要添加的一个条件是______.
答案:
解析:解:添加,
,,,
≌
故答案为:.
由题意可得,,则添加,由SAS判定≌.
本题考查了全等三角形的判定,灵活运用全等三角形的判定是本题的关键.
8.如图,已知,若以“SAS”为依据判定≌,还需添加的一个条件是?
?
??.
答案:
解析:【分析】
本题主要考查了全等三角形的判定,关键是熟练掌握全等三角形的判定方法根据公共边和已知的角可得结论.
【解答】
解:,,,
≌.
故答案为.
9.如图所示,已知,,若要用“SAS”去证≌,则需添加的条件是______.
答案:
解析:解:需要添加条件为,
理由是:,
,
即,
,
,
在和中
≌,
故答案为:.
求出,根据平行线的性质得出,根据全等三角形的判定得出即可.
本题考查了全等三角形的判定定理和平行线的性质,能熟记全等三角形的判定定理的内容是解此题的关键,注意:全等三角形的判定定理有:SAS,AAS,ASA,SSS,直角三角形全等还有HL定理.
10.如图,在四边形ABCD中,由,得________________若,结合________________,则.
答案:ABD;CDB;BD;DB
解析:【分析】
本题考查平行线的性质、全等三角形的判定,熟练掌握平行线的性质、全等三角形的判定是解题的关键.
根据两直线平行,内错角相等和全等三角形的判定方法SAS,即可求解.
【解答】
解:,
,
在和中,
.
故答案为ABD;CDB;BD;DB.
11.如图,中,,点D,E在BC边上,若要以“SAS”为依据说明≌,还要添加的条件为??????????.
答案:
解析:【分析】
根据可得,再添加可利用SAS判定≌.
此题主要考查了全等三角形的判定,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
【解答】
解:添加的条件为,
,
在和中,
≌,
故答案为:.
12.如图,已知,,要使,若以“SAS”为依据,则补充的条件是________.
答案:
解析:【分析】
本题考查了全等三角形的判定;题目是开放型题目,根据已知条件结合判定方法,找出所需条件,一般答案不唯一,只要符合要求即可.先根据,等号两边都加上,得到,由已知,要使≌,根据全等三角形的判定定理ASA:添上.
【解答】
解:,,即.
又,补充的条件是,
则在与中.
故答案为.
三、解答题
13.如图,点D在BC上,,,下面三个条件:;;,请你从所给条件中选一个条件,使≌,并证明两三角形全等.
答案:解:选,
,,
,
在和中,,
≌.
解析:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.根据结合三角形内角和定理可得,再有条件,添加可利用SAS定理判定≌.
14.如图,,,,,点P在线段AB上以的速度,由A向B运动,同时点Q在线段BD上由B向D运动;设点P的运动时间为t秒.
_______用含t的代数式表示
如图1,若点Q的运动速度与点P的运动速度相等,当运动时间秒时,与是否全等?并说明理由.
如图2,将“,”改为“”,其余条件不变;设点Q的运动速度为,是否存在实数x,使得与全等?若存在,求出相应的x、t的值;若不存在,请说明理由.
答案:解:;
≌,
理由:当时,,,
又,
在和中,
,
≌;
若≌,
则,,
则
解得;
若≌,
则,,
则
解得:;
综上所述,存在或,使得与全等.
解析:【分析】
本题主要考查了全等三角形的判定与性质,两边及其夹角分别对应相等的两个三角形全等.在解题时注意分类讨论思想的运用.
直接由题意即可求得答案;
利用SAS即可证得≌;
由≌,≌,分两种情况:,,,,建立方程组求得答案即可.
【解答】
解:由题意可得:,
故答案为;
见答案;
见答案.
15.如图,已知,AB与ED交于点M,BC与ED,AD分别交于点F,请写出图中其余的全等三角形除外,并选择其中的一对加以证明.
答案:解:≌,≌,≌.
选择≌,
理由如下:
≌,
,,,
,
在和中,
≌.
解析:本题考查三角形全等的判定方法以及全等三角形的性质;判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.找到两三角形全等的条件,三角形全等就写出来,选择一组证明即可.
16.【问题情境】
课外兴趣小组活动时,老师提出了如下问题:
如图,中,若,,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD至点E,使,连接请根据小明的方法思考:
Ⅰ由已知和作图能得到≌,依据是______.
A.SSS????????????
Ⅱ由“三角形的三边关系”可求得AD的取值范围是______.
解后反思:题目中出现“中点”、“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形之中.
【初步运用】
如图,AD是的中线,BE交AC于E,交AD于F,且若,,求线段BF的长.
答案:B?
解析:解:Ⅰ在和中,
,
≌,
故选:B;
Ⅱ≌,
,
,
故答案为:.
延长AD到M,使,连接BM,如图
是中线,
,
在和中,
,
≌,
,,
,
,
,
,
,
,
,
,
即.
Ⅰ根据全等三角形的判定定理解答.
Ⅱ根据三角形的三边关系计算.
延长AD到M,使,连接BM,证明≌,根据全等三角形的性质解答.
本题考查的是全等三角形的判定和性质、三角形三边关系以及勾股定理的应用,掌握全等三角形的判定定理和性质定理是解题的关键.
17.探究问题:如图1,在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足,连接EF,求证:.
方法感悟:延长CB至G,使,
可证≌,,
,
又,
?,即,
又,,≌,
,故DE;
方法迁移:如图2将沿斜边翻折得到,点E、F分别为DC、BC上的点,且试猜想DE、BF、EF之间有何数量关系,并证明你的猜想.
形成模型:如图3,在四边形ABCD中,,E、F分别为DC、BC上的点,,,可得.
模型应用:如图4,在某次军事演习中,舰艇甲在指挥中心处北偏西的A处,舰艇乙在指挥中心南偏东的B处,并且两舰艇到指挥中心的距离相等。接到行动指令后,舰艇甲向正东方向以60海里小时的速度前进,舰艇乙沿北偏东的方向以80海里小时的速度前进,小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间夹角为,试求此时两舰艇之间的距离若能得到的模型,可直接应用模型解题的结论,不需再次证明全等.
答案:解:,理由如下:
延长CB到G使,如图:
是沿斜边翻折而得,
,,
在和中,
,
≌,
,
,
,
,
在和中,
,
≌,
,
即:;
延长延长CB到G使,如图:
,
,
,
在和中,
,
≌,
,,
,
,
,
,
在和中,
,
和,
,
即:;
延长AE和BF交于C,连接EF,如图:
由题意得:,,
,且,,
,
,
符合中的模型:
,
海里,
海里,
海里,
所以此时两舰艇之间的距离为210海里.
解析:本题主要考查全等三角形的判定和性质,解决本题的关键是构造全等三角形.
延长CB到G使,从而构造≌,从而,,于是≌,从而得到结论;
方法和思路同;
由题意得:,,,符合中的模型,故EF,从而得出结论.
18.在解决线段数量关系问题中,如果条件中有角平分线,经常采用下面构造全等三角形的解决思路.
如:在图1中,若C是的平分线OP上一点,点A在OM上,此时,在ON截取,连接BC,根据三角形全等的判定,容易构造出全等三角形和,参考上面的方法,解答下列问题:
如图2,在非等边中,,AD、CE分别是、的平分线,且AD、CE交于点求证:.
答案:证明:如图所示,在AC上截取,连结FG.
是的平分线,CE是的平分线,
,.
在和中,
≌,
,
,
,
,
,
,
,
,
在和中,
≌,
,
.
解析:本题考查了全等三角形的判定和性质,角平分线的定义,平角的定义,三角形外角的性质,解题关键是运用阅读材料中的方法构造全等三角形解题时,在AC上截取,连结FG,先证明≌,得出,再根据已知条件和三角形外角的性质证明,由平角的定义可得,然后证明≌,得出,即可证明.
1.3探索三角形全等的条件SAS
一、选择题
1.如图,已知,要使≌,只需要添加一个条件是
A.
B.
C.
D.
2.如图,已知,,,由这三个条件,就可得出≌,依据的判定方法是
A.
边边边
B.
边角边
C.
角边角
D.
角角边
3.如图,AC、BD相交于点O,,若用“SAS”说明≌,则还需要加上条件
A.
B.
C.
D.
4.如图,用“SAS”证明,若已知,,则还需
A.
B.
C.
D.
5.如图,在和中,如果,,那么补充条件后能应用“SAS”说明≌的是
A.
B.
C.
D.
6.在和中,下列条件:;;;;;其中,能用“SAS”证明≌的一组是
A.
B.
C.
D.
二、填空题
7.如图,点D、E分别在线段AB、AC上,且,若由SAS判定≌,则需要添加的一个条件是______.
8.如图,已知,若以“SAS”为依据判定≌,还需添加的一个条件是?
?
??.
9.如图所示,已知,,若要用“SAS”去证≌,则需添加的条件是______.
10.如图,在四边形ABCD中,由,得________________若,结合________________,则.
11.如图,中,,点D,E在BC边上,若要以“SAS”为依据说明≌,还要添加的条件为??????????.
12.如图,已知,,要使,若以“SAS”为依据,则补充的条件是________.
三、解答题
13.如图,点D在BC上,,,下面三个条件:;;,请你从所给条件中选一个条件,使≌,并证明两三角形全等.
14.如图,,,,,点P在线段AB上以的速度,由A向B运动,同时点Q在线段BD上由B向D运动;设点P的运动时间为t秒.
_______用含t的代数式表示
(2)如图1,若点Q的运动速度与点P的运动速度相等,当运动时间秒时,与是否全等?并说明理由.
(3)如图2,将“,”改为“”,其余条件不变;设点Q的运动速度为,是否存在实数x,使得与全等?若存在,求出相应的x、t的值;若不存在,请说明理由.
15.如图,已知,AB与ED交于点M,BC与ED,AD分别交于点F,请写出图中其余的全等三角形除外,并选择其中的一对加以证明.
16.【问题情境】
课外兴趣小组活动时,老师提出了如下问题:
如图,中,若,,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD至点E,使,连接请根据小明的方法思考:
Ⅰ由已知和作图能得到≌,依据是______.
A.SSS????????????
Ⅱ由“三角形的三边关系”可求得AD的取值范围是______.
解后反思:题目中出现“中点”、“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形之中.
【初步运用】
如图,AD是的中线,BE交AC于E,交AD于F,且若,,求线段BF的长.
17.探究问题:如图1,在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足,连接EF,求证:.
方法感悟:延长CB至G,使,
可证≌,,
,
又,
?,即,
又,,≌,
,故DE;
方法迁移:如图2将沿斜边翻折得到,点E、F分别为DC、BC上的点,且试猜想DE、BF、EF之间有何数量关系,并证明你的猜想.
形成模型:如图3,在四边形ABCD中,,E、F分别为DC、BC上的点,,,可得.
模型应用:如图4,在某次军事演习中,舰艇甲在指挥中心处北偏西的A处,舰艇乙在指挥中心南偏东的B处,并且两舰艇到指挥中心的距离相等。接到行动指令后,舰艇甲向正东方向以60海里小时的速度前进,舰艇乙沿北偏东的方向以80海里小时的速度前进,小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间夹角为,试求此时两舰艇之间的距离若能得到的模型,可直接应用模型解题的结论,不需再次证明全等.
18.在解决线段数量关系问题中,如果条件中有角平分线,经常采用下面构造全等三角形的解决思路.
如:在图1中,若C是的平分线OP上一点,点A在OM上,此时,在ON截取,连接BC,根据三角形全等的判定,容易构造出全等三角形和,参考上面的方法,解答下列问题:
如图2,在非等边中,,AD、CE分别是、的平分线,且AD、CE交于点求证:.
苏科版数学八年级培优训练(教师卷)
1.3探索三角形全等的条件SAS
一、选择题
1.如图,已知,要使≌,只需要添加一个条件是
A.
B.
C.
D.
答案:D
解析:解:A、根据,和不能推出≌,故本选项不符合题意;
B、根据,和不能推出≌,故本选项不符合题意;
C、根据,和不能推出≌,故本选项不符合题意;
D、根据,,能推出≌,故本选项符合题意;
故选:D.
根据全等三角形的判定定理逐个判断即可.
本题考查了全等三角形的判定定理,能熟记全等三角形的判定定理的内容是解此题的关键,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS等.
2.如图,已知,,,由这三个条件,就可得出≌,依据的判定方法是
A.
边边边
B.
边角边
C.
角边角
D.
角角边
答案:B
解析:解:,
,
,
在和中,
,
≌,
故选:B.
根据SAS证明三角形全等即可解决问题.
本题考查全等三角形的判定,解题的关键是熟练掌握全等三角形的判定方法,属于中考常考题型.
3.如图,AC、BD相交于点O,,若用“SAS”说明≌,则还需要加上条件
A.
B.
C.
D.
答案:B
解析:【分析】
本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.已有条件,,若用“SAS”说明≌必须添加边相等,根据判定方法可得应添加.
【解答】
解:还需要加上条件,
在和中,
≌,
故选:B.
4.如图,用“SAS”证明,若已知,,则还需
A.
B.
C.
D.
答案:C
解析:【分析】
本题考查全等三角形的判定,根据题目中给出的条件,,要用“SAS”还缺少条件是夹角:,筛选答案可选出C.
【解答】
解:已知两边分别相等,若其夹角相等,则符合“SAS”,
由得,
即,
故选C.
5.如图,在和中,如果,,那么补充条件后能应用“SAS”说明≌的是
A.
B.
C.
D.
答案:D
解析:【分析】
本题考查了三角形全等的条件,判定三角形全等一定要结合图形上的位置关系,从而选择方法.应用从的两边是AB、BC,的两边是DE、EF分析,找到需要相等的两边.
【解答】
解:两边和它们的夹角对应相等的两个三角形全等.
的两边是AB、BC,的两边是DE、EF,故BC即可.
故选D.
6.在和中,下列条件:;;;;;其中,能用“SAS”证明≌的一组是
A.
B.
C.
D.
答案:D
解析:【试题解析】
【分析】
此题主要考查了全等三角形的判定,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.由于全等三角形的六个元素,其中找到能用“SAS”证明≌的元素,由此即可求解.?
【解答】
解:根据题意,其中能用“SAS”证明≌的,和,
故选D.
二、填空题
7.如图,点D、E分别在线段AB、AC上,且,若由SAS判定≌,则需要添加的一个条件是______.
答案:
解析:解:添加,
,,,
≌
故答案为:.
由题意可得,,则添加,由SAS判定≌.
本题考查了全等三角形的判定,灵活运用全等三角形的判定是本题的关键.
8.如图,已知,若以“SAS”为依据判定≌,还需添加的一个条件是?
?
??.
答案:
解析:【分析】
本题主要考查了全等三角形的判定,关键是熟练掌握全等三角形的判定方法根据公共边和已知的角可得结论.
【解答】
解:,,,
≌.
故答案为.
9.如图所示,已知,,若要用“SAS”去证≌,则需添加的条件是______.
答案:
解析:解:需要添加条件为,
理由是:,
,
即,
,
,
在和中
≌,
故答案为:.
求出,根据平行线的性质得出,根据全等三角形的判定得出即可.
本题考查了全等三角形的判定定理和平行线的性质,能熟记全等三角形的判定定理的内容是解此题的关键,注意:全等三角形的判定定理有:SAS,AAS,ASA,SSS,直角三角形全等还有HL定理.
10.如图,在四边形ABCD中,由,得________________若,结合________________,则.
答案:ABD;CDB;BD;DB
解析:【分析】
本题考查平行线的性质、全等三角形的判定,熟练掌握平行线的性质、全等三角形的判定是解题的关键.
根据两直线平行,内错角相等和全等三角形的判定方法SAS,即可求解.
【解答】
解:,
,
在和中,
.
故答案为ABD;CDB;BD;DB.
11.如图,中,,点D,E在BC边上,若要以“SAS”为依据说明≌,还要添加的条件为??????????.
答案:
解析:【分析】
根据可得,再添加可利用SAS判定≌.
此题主要考查了全等三角形的判定,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
【解答】
解:添加的条件为,
,
在和中,
≌,
故答案为:.
12.如图,已知,,要使,若以“SAS”为依据,则补充的条件是________.
答案:
解析:【分析】
本题考查了全等三角形的判定;题目是开放型题目,根据已知条件结合判定方法,找出所需条件,一般答案不唯一,只要符合要求即可.先根据,等号两边都加上,得到,由已知,要使≌,根据全等三角形的判定定理ASA:添上.
【解答】
解:,,即.
又,补充的条件是,
则在与中.
故答案为.
三、解答题
13.如图,点D在BC上,,,下面三个条件:;;,请你从所给条件中选一个条件,使≌,并证明两三角形全等.
答案:解:选,
,,
,
在和中,,
≌.
解析:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.根据结合三角形内角和定理可得,再有条件,添加可利用SAS定理判定≌.
14.如图,,,,,点P在线段AB上以的速度,由A向B运动,同时点Q在线段BD上由B向D运动;设点P的运动时间为t秒.
_______用含t的代数式表示
如图1,若点Q的运动速度与点P的运动速度相等,当运动时间秒时,与是否全等?并说明理由.
如图2,将“,”改为“”,其余条件不变;设点Q的运动速度为,是否存在实数x,使得与全等?若存在,求出相应的x、t的值;若不存在,请说明理由.
答案:解:;
≌,
理由:当时,,,
又,
在和中,
,
≌;
若≌,
则,,
则
解得;
若≌,
则,,
则
解得:;
综上所述,存在或,使得与全等.
解析:【分析】
本题主要考查了全等三角形的判定与性质,两边及其夹角分别对应相等的两个三角形全等.在解题时注意分类讨论思想的运用.
直接由题意即可求得答案;
利用SAS即可证得≌;
由≌,≌,分两种情况:,,,,建立方程组求得答案即可.
【解答】
解:由题意可得:,
故答案为;
见答案;
见答案.
15.如图,已知,AB与ED交于点M,BC与ED,AD分别交于点F,请写出图中其余的全等三角形除外,并选择其中的一对加以证明.
答案:解:≌,≌,≌.
选择≌,
理由如下:
≌,
,,,
,
在和中,
≌.
解析:本题考查三角形全等的判定方法以及全等三角形的性质;判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.找到两三角形全等的条件,三角形全等就写出来,选择一组证明即可.
16.【问题情境】
课外兴趣小组活动时,老师提出了如下问题:
如图,中,若,,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD至点E,使,连接请根据小明的方法思考:
Ⅰ由已知和作图能得到≌,依据是______.
A.SSS????????????
Ⅱ由“三角形的三边关系”可求得AD的取值范围是______.
解后反思:题目中出现“中点”、“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形之中.
【初步运用】
如图,AD是的中线,BE交AC于E,交AD于F,且若,,求线段BF的长.
答案:B?
解析:解:Ⅰ在和中,
,
≌,
故选:B;
Ⅱ≌,
,
,
故答案为:.
延长AD到M,使,连接BM,如图
是中线,
,
在和中,
,
≌,
,,
,
,
,
,
,
,
,
,
即.
Ⅰ根据全等三角形的判定定理解答.
Ⅱ根据三角形的三边关系计算.
延长AD到M,使,连接BM,证明≌,根据全等三角形的性质解答.
本题考查的是全等三角形的判定和性质、三角形三边关系以及勾股定理的应用,掌握全等三角形的判定定理和性质定理是解题的关键.
17.探究问题:如图1,在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足,连接EF,求证:.
方法感悟:延长CB至G,使,
可证≌,,
,
又,
?,即,
又,,≌,
,故DE;
方法迁移:如图2将沿斜边翻折得到,点E、F分别为DC、BC上的点,且试猜想DE、BF、EF之间有何数量关系,并证明你的猜想.
形成模型:如图3,在四边形ABCD中,,E、F分别为DC、BC上的点,,,可得.
模型应用:如图4,在某次军事演习中,舰艇甲在指挥中心处北偏西的A处,舰艇乙在指挥中心南偏东的B处,并且两舰艇到指挥中心的距离相等。接到行动指令后,舰艇甲向正东方向以60海里小时的速度前进,舰艇乙沿北偏东的方向以80海里小时的速度前进,小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间夹角为,试求此时两舰艇之间的距离若能得到的模型,可直接应用模型解题的结论,不需再次证明全等.
答案:解:,理由如下:
延长CB到G使,如图:
是沿斜边翻折而得,
,,
在和中,
,
≌,
,
,
,
,
在和中,
,
≌,
,
即:;
延长延长CB到G使,如图:
,
,
,
在和中,
,
≌,
,,
,
,
,
,
在和中,
,
和,
,
即:;
延长AE和BF交于C,连接EF,如图:
由题意得:,,
,且,,
,
,
符合中的模型:
,
海里,
海里,
海里,
所以此时两舰艇之间的距离为210海里.
解析:本题主要考查全等三角形的判定和性质,解决本题的关键是构造全等三角形.
延长CB到G使,从而构造≌,从而,,于是≌,从而得到结论;
方法和思路同;
由题意得:,,,符合中的模型,故EF,从而得出结论.
18.在解决线段数量关系问题中,如果条件中有角平分线,经常采用下面构造全等三角形的解决思路.
如:在图1中,若C是的平分线OP上一点,点A在OM上,此时,在ON截取,连接BC,根据三角形全等的判定,容易构造出全等三角形和,参考上面的方法,解答下列问题:
如图2,在非等边中,,AD、CE分别是、的平分线,且AD、CE交于点求证:.
答案:证明:如图所示,在AC上截取,连结FG.
是的平分线,CE是的平分线,
,.
在和中,
≌,
,
,
,
,
,
,
,
,
在和中,
≌,
,
.
解析:本题考查了全等三角形的判定和性质,角平分线的定义,平角的定义,三角形外角的性质,解题关键是运用阅读材料中的方法构造全等三角形解题时,在AC上截取,连结FG,先证明≌,得出,再根据已知条件和三角形外角的性质证明,由平角的定义可得,然后证明≌,得出,即可证明.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
