2021—2022学年湘教版八年级数学上册 2.1.3三角形内角和定理 课件(共19张)
文档属性
| 名称 | 2021—2022学年湘教版八年级数学上册 2.1.3三角形内角和定理 课件(共19张) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-23 00:00:00 | ||
图片预览



文档简介
(共19张PPT)
湘教版八年级数学上
2.1三角形内角和定理(3)
1、尝试用多种方法证明三角形内角和定理,体会证明中辅助线的作用。
2、通过练习,达到灵活应用三角形内角和定理进行简单的计算和证明。
学
习
目
标
B
c
A1
A2
A3
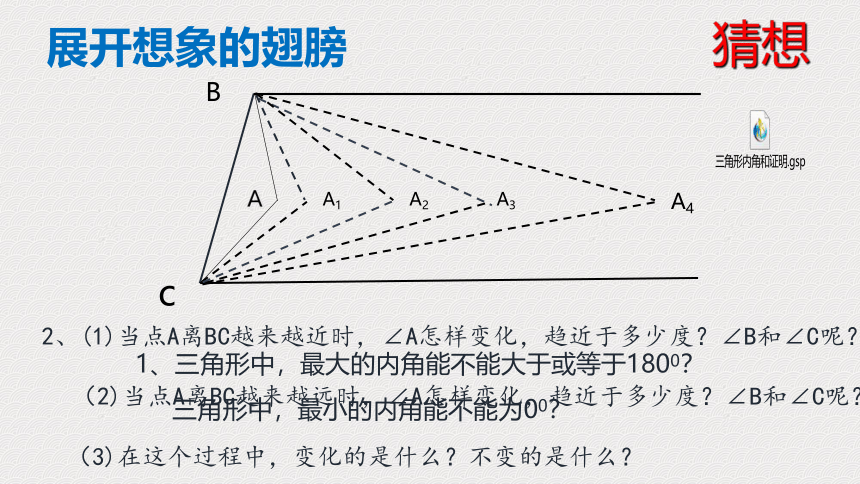
展开想象的翅膀
1、三角形中,最大的内角能不能大于或等于1800?
三角形中,最小的内角能不能为00?
A4
A
猜想
2、(1)当点A离BC越来越近时,∠A怎样变化,趋近于多少度?∠B和∠C呢?
(2)当点A离BC越来越远时,∠A怎样变化,趋近于多少度?∠B和∠C呢?
(3)在这个过程中,变化的是什么?不变的是什么?
七嘴八舌话证明
三角形的内角和是1800
度
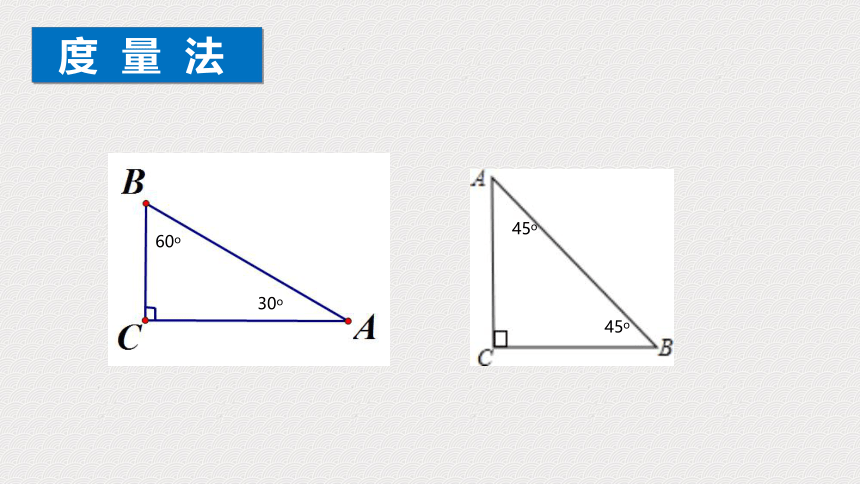
量
法
60o
30o
45o
45o
A
B
C
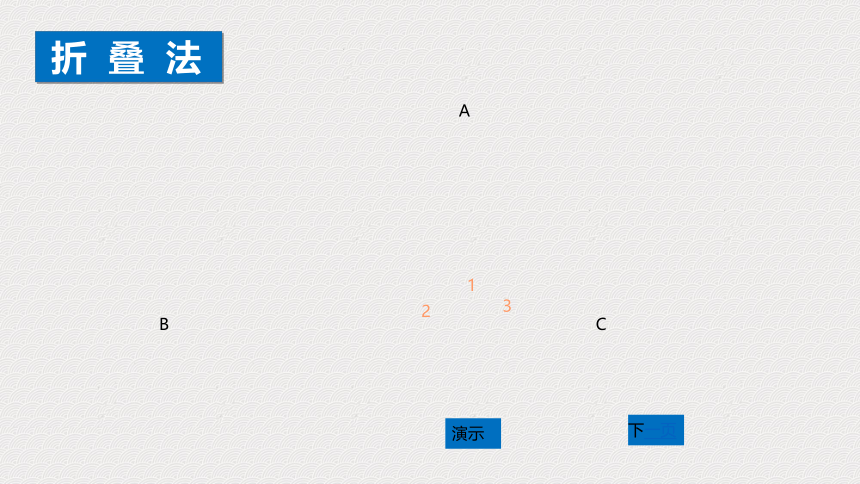
演示
下一页
1
2
3
折
叠
法
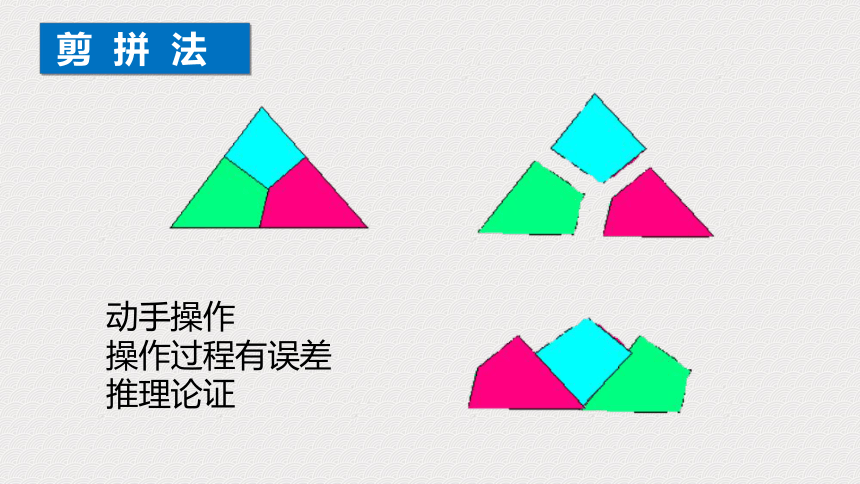
剪
拼
法
动手操作
操作过程有误差
推理论证
三角形三个内角的和等于1800
B
C
A
已知:如图,
△ABC.
求证:∠A+∠B+∠C=1800.
世事洞明皆学问
1.
平角的度数是180°
2.
两直线平行,同旁内角的和是180°
3.
邻补角
有什么方法可以得到180°
转
化
思
想
验证:三角形的三个内角和是180°
图1
图2
A
B
C
C
B
A
B
C
A
B
A
B
C
D
E
辅助线:在原来图形上添加的线叫做辅助线.
尝试一下
已知:如图,
△ABC.
求证:∠A+∠B+∠C=1800.
C
A
B
E
D
2
1
3
A
B
C
D
D
C
F
A
E
B
C
A
B
P
C
A
B
P
拓展延伸
1.已知三角形三个内角的度数之比为1:3:5,求这三个内角的度数。
小试牛刀
2.
如图,在△ABC中,若P点是∠ABC和∠ACB的角平分线的交点,∠A=500,求∠P的度数。
(1)一个三角形中能有两个直角(
)
(2)一个三角形中能有两个钝角吗?(
)
(3)三个内角都能小于600(
)
(4)一个三角形最多有一个钝角(
)
(5)
一个三角形至少有两个锐角(
)
2、思考并判断
√
√
×
×
×
A
B
C
D
已知:如图,四边形ABCD是一个任意四边形。
求证:∠A+∠B+∠C+∠D=3600
再试牛刀
转
化
思
想
本节课里你学到了什么?(梳理)
回
顾
与
小
结
猜
想
尝
试
解
决
动
手
操
作
发
现
推
理
证
明
得
出
结
论
1.(1)在△ABC中,∠A=35°,∠
B=43°,则∠
C=
。
(2)
在△ABC中,
∠A=40°,∠A=2∠B,则∠C
=
。
1020
1200
当堂达标
?
B
900
非常感谢您的观看
THANK
YOU
FOR
YOUR
WATCHING
湘教版八年级数学上
2.1三角形内角和定理(3)
1、尝试用多种方法证明三角形内角和定理,体会证明中辅助线的作用。
2、通过练习,达到灵活应用三角形内角和定理进行简单的计算和证明。
学
习
目
标
B
c
A1
A2
A3
展开想象的翅膀
1、三角形中,最大的内角能不能大于或等于1800?
三角形中,最小的内角能不能为00?
A4
A
猜想
2、(1)当点A离BC越来越近时,∠A怎样变化,趋近于多少度?∠B和∠C呢?
(2)当点A离BC越来越远时,∠A怎样变化,趋近于多少度?∠B和∠C呢?
(3)在这个过程中,变化的是什么?不变的是什么?
七嘴八舌话证明
三角形的内角和是1800
度
量
法
60o
30o
45o
45o
A
B
C
演示
下一页
1
2
3
折
叠
法
剪
拼
法
动手操作
操作过程有误差
推理论证
三角形三个内角的和等于1800
B
C
A
已知:如图,
△ABC.
求证:∠A+∠B+∠C=1800.
世事洞明皆学问
1.
平角的度数是180°
2.
两直线平行,同旁内角的和是180°
3.
邻补角
有什么方法可以得到180°
转
化
思
想
验证:三角形的三个内角和是180°
图1
图2
A
B
C
C
B
A
B
C
A
B
A
B
C
D
E
辅助线:在原来图形上添加的线叫做辅助线.
尝试一下
已知:如图,
△ABC.
求证:∠A+∠B+∠C=1800.
C
A
B
E
D
2
1
3
A
B
C
D
D
C
F
A
E
B
C
A
B
P
C
A
B
P
拓展延伸
1.已知三角形三个内角的度数之比为1:3:5,求这三个内角的度数。
小试牛刀
2.
如图,在△ABC中,若P点是∠ABC和∠ACB的角平分线的交点,∠A=500,求∠P的度数。
(1)一个三角形中能有两个直角(
)
(2)一个三角形中能有两个钝角吗?(
)
(3)三个内角都能小于600(
)
(4)一个三角形最多有一个钝角(
)
(5)
一个三角形至少有两个锐角(
)
2、思考并判断
√
√
×
×
×
A
B
C
D
已知:如图,四边形ABCD是一个任意四边形。
求证:∠A+∠B+∠C+∠D=3600
再试牛刀
转
化
思
想
本节课里你学到了什么?(梳理)
回
顾
与
小
结
猜
想
尝
试
解
决
动
手
操
作
发
现
推
理
证
明
得
出
结
论
1.(1)在△ABC中,∠A=35°,∠
B=43°,则∠
C=
。
(2)
在△ABC中,
∠A=40°,∠A=2∠B,则∠C
=
。
1020
1200
当堂达标
?
B
900
非常感谢您的观看
THANK
YOU
FOR
YOUR
WATCHING
同课章节目录
