人教版七年级数学上册第三章一元一次方程3.4 第4课时 电话计费问题 课件(22张ppt)
文档属性
| 名称 | 人教版七年级数学上册第三章一元一次方程3.4 第4课时 电话计费问题 课件(22张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-23 16:52:48 | ||
图片预览








文档简介
(共22张PPT)
第三章
一元一次方程
3.4
实际问题与一元一次方程
第4课时
电话计费问题
教学目标
1.体验建立方程模型解决问题的一般过程;
2.体会分类思想和方程思想,增强应用意识和应用能力.
问题:
小平的爸爸新买了一部手机,他从电信公司了解到现在有两种移动电话计费方式:
方式一
方式二
月租费
30元/月
0
本地通话费
0.30元/分
0.40元/分
他正在为选哪种方式犹豫呢?你能帮助他作个选择吗?
(1)一个月内通话200分和300分钟,按两种计费方式各需缴费多少元?
方式一
方式二
200分
300分
(2)对于某个通话时间,两种计费方式的收费会一样吗?(列式计算)
由此可知,如果一个月内通话_____分钟,那么两种计费方式的收费相同.
(3)怎样选择计费方式更省钱呢?
如果一个月内累计通话时间不足_____分,那么选择“方式二”收费少;如果一个月内累计通话时间超过_____分,那么选择________收费少.
(4)根据以上解题过程,你能为小平的爸爸作选择了吗?
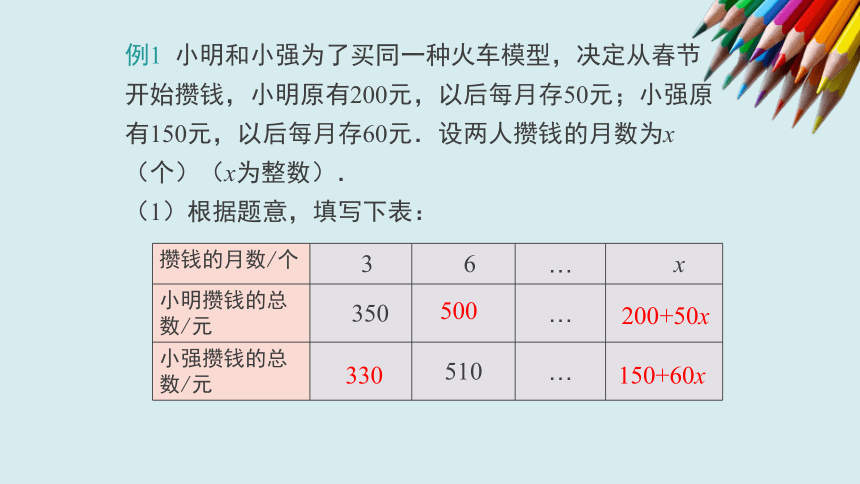
例1
小明和小强为了买同一种火车模型,决定从春节开始攒钱,小明原有200元,以后每月存50元;小强原有150元,以后每月存60元.设两人攒钱的月数为x(个)(x为整数).
(1)根据题意,填写下表:
攒钱的月数/个
3
6
…
x
小明攒钱的总数/元
350
…
小强攒钱的总数/元
510
…
330
500
200+50x
150+60x
(2)在几个月后小明与小强攒钱的总数相同?此时他们各有多少钱?
(2)
根据题意,得200+50x=150+60x,
解得x=5.
所以150+60x=450.
答:在5个月后小明与小强攒钱的总数相同,此时每人有450元钱.
(3)若这种火车模型的价格为780元,他们谁能够先买到该模型?
(3)
根据题意,由200+50x=780,解得x=11.6,故小明在12个月后攒钱的总数超过780元.
由150+60x=780,解得x=10.5,
故小强在11个月后攒钱的总数超过780元.
所以小强能够先买到该模型.
方法总结:解决此类问题的关键是能够根据已知条件找到合适的分段点,然后建立方程模型分类讨论,从而得出整体选择方案.
例2.移动公司推出两种智能手机上网流量包:
月使用费(元)
含上网流量(M)
流量超出部分(元/M)
A种
30
320
0.2
B种
50
550
0.1
如何选择流量包更划算?
解:设一个月内使用的流量为
x
M,根据题意,当x
在不同范围内取值时,两种流量包计费如下表:
使用流量
x(M)
A种计费(元)
B种计费(元)
x小于等于320
30
50
x大于320且小于550
30+0.2(x-320)
50
x等于550
76
50
x大于550
30+0.2(x-320)
50+0.1(x-550)
(1)
当
x
≤
320
时,流量包A
计费少(30元);
(2)
当
320<x<420
时,流量包A
计费少(<50元);
(3)
当
x
=
420时,两种流量包计费相等,都是50元;
(4)
当
420<x<550
时,流量包B
计费少(50元);
(5)
当
x
=
550
时,流量包B
计费少(50元);
(6)
当
x>550
时,流量包B
计费少.
综上所述,
当月使用流量小于
420
M
时,选择流量包A
划算;
当月使用流量等于
420
M
时,两种流量包费用一样;
当月使用流量大于
420
M
时,选择流量包B
划算.
课堂练习
1.甲、乙两种型号货车出租价格如下表:
(1)设运输货物里程为s
km,根据上表列表说明,当s在不同范围内取值时,甲、乙两种货车如何计费.
(2)观察你的列表,你能从中发现如何根据运输里程选择较省钱的租车方式吗?通过计算验证你的看法.
起步价/元
限定里程/km
超限定里程(元/km)
甲
108
80
3
乙
150
100
2
2.
某市为鼓励居民节约用水,对自来水用户按分段
计费方式收取水费:若每户每月用水不超过
7m3,
则按
2
元/m3
收费;若每户每月用水超过
7
m3,
则超过的部分按
3元/m3
收费.
如果某居民户去年
12月缴纳了
53
元水费,那么这户居民去年12月
的用水量为_______m3.
20
档次
每户每月用电数(度)
执行电价(元/度)
第一档
小于等于200
0.55
第二档
大于200小于400
0.6
第三档
大于等于400
0.85
3.为鼓励居民节约用电,某省试行阶段电价收费制,具体执行方案如表:
例如:一户居民七月份用电420度,则需缴电费420×0.85=357(元).
某户居民五、六月份共用电500度,缴电费290.5元.已知该用户六月份用电量大于五月份,且五、六月份的用电量均小于400度.问该户居民五、六月份各用电多少度?
解析:某户居民五、六月份共用电500度,就可以得出
每月用电量不可能都在第一档,分情况讨论,当5月份
用电量为x度≤200度,6月份用电(500-x)度,
当5月份用电量为x度>200度,六月份用电量为
(500-x)度,分别建立方程求出其解即可.
解:当5月份用电量为x度≤200度,6月份用电(500-x)度,由题意得
0.55x+0.6×(500-x)=290.5,
解得x=190,
∴6月份用电500-x=310(度).
当5月份用电量为x度>200度,六月份用电量为(500-x)度>200度,由题意得
0.6x+0.6×(500-x)=290.5,
方程无解,
∴该情况不符合题意.
答:该户居民五、六月份分别用电190度、310度.
课堂小结
1.
解决电话计费问题需要明确“哪种计费方式更省
钱”与“主叫时间”有关.
2.
此类问题的关键是能够根据已知条件找到合适
的分段点,然后建立方程模型分类讨论,从而
得出整体选择方案.
第三章
一元一次方程
3.4
实际问题与一元一次方程
第4课时
电话计费问题
教学目标
1.体验建立方程模型解决问题的一般过程;
2.体会分类思想和方程思想,增强应用意识和应用能力.
问题:
小平的爸爸新买了一部手机,他从电信公司了解到现在有两种移动电话计费方式:
方式一
方式二
月租费
30元/月
0
本地通话费
0.30元/分
0.40元/分
他正在为选哪种方式犹豫呢?你能帮助他作个选择吗?
(1)一个月内通话200分和300分钟,按两种计费方式各需缴费多少元?
方式一
方式二
200分
300分
(2)对于某个通话时间,两种计费方式的收费会一样吗?(列式计算)
由此可知,如果一个月内通话_____分钟,那么两种计费方式的收费相同.
(3)怎样选择计费方式更省钱呢?
如果一个月内累计通话时间不足_____分,那么选择“方式二”收费少;如果一个月内累计通话时间超过_____分,那么选择________收费少.
(4)根据以上解题过程,你能为小平的爸爸作选择了吗?
例1
小明和小强为了买同一种火车模型,决定从春节开始攒钱,小明原有200元,以后每月存50元;小强原有150元,以后每月存60元.设两人攒钱的月数为x(个)(x为整数).
(1)根据题意,填写下表:
攒钱的月数/个
3
6
…
x
小明攒钱的总数/元
350
…
小强攒钱的总数/元
510
…
330
500
200+50x
150+60x
(2)在几个月后小明与小强攒钱的总数相同?此时他们各有多少钱?
(2)
根据题意,得200+50x=150+60x,
解得x=5.
所以150+60x=450.
答:在5个月后小明与小强攒钱的总数相同,此时每人有450元钱.
(3)若这种火车模型的价格为780元,他们谁能够先买到该模型?
(3)
根据题意,由200+50x=780,解得x=11.6,故小明在12个月后攒钱的总数超过780元.
由150+60x=780,解得x=10.5,
故小强在11个月后攒钱的总数超过780元.
所以小强能够先买到该模型.
方法总结:解决此类问题的关键是能够根据已知条件找到合适的分段点,然后建立方程模型分类讨论,从而得出整体选择方案.
例2.移动公司推出两种智能手机上网流量包:
月使用费(元)
含上网流量(M)
流量超出部分(元/M)
A种
30
320
0.2
B种
50
550
0.1
如何选择流量包更划算?
解:设一个月内使用的流量为
x
M,根据题意,当x
在不同范围内取值时,两种流量包计费如下表:
使用流量
x(M)
A种计费(元)
B种计费(元)
x小于等于320
30
50
x大于320且小于550
30+0.2(x-320)
50
x等于550
76
50
x大于550
30+0.2(x-320)
50+0.1(x-550)
(1)
当
x
≤
320
时,流量包A
计费少(30元);
(2)
当
320<x<420
时,流量包A
计费少(<50元);
(3)
当
x
=
420时,两种流量包计费相等,都是50元;
(4)
当
420<x<550
时,流量包B
计费少(50元);
(5)
当
x
=
550
时,流量包B
计费少(50元);
(6)
当
x>550
时,流量包B
计费少.
综上所述,
当月使用流量小于
420
M
时,选择流量包A
划算;
当月使用流量等于
420
M
时,两种流量包费用一样;
当月使用流量大于
420
M
时,选择流量包B
划算.
课堂练习
1.甲、乙两种型号货车出租价格如下表:
(1)设运输货物里程为s
km,根据上表列表说明,当s在不同范围内取值时,甲、乙两种货车如何计费.
(2)观察你的列表,你能从中发现如何根据运输里程选择较省钱的租车方式吗?通过计算验证你的看法.
起步价/元
限定里程/km
超限定里程(元/km)
甲
108
80
3
乙
150
100
2
2.
某市为鼓励居民节约用水,对自来水用户按分段
计费方式收取水费:若每户每月用水不超过
7m3,
则按
2
元/m3
收费;若每户每月用水超过
7
m3,
则超过的部分按
3元/m3
收费.
如果某居民户去年
12月缴纳了
53
元水费,那么这户居民去年12月
的用水量为_______m3.
20
档次
每户每月用电数(度)
执行电价(元/度)
第一档
小于等于200
0.55
第二档
大于200小于400
0.6
第三档
大于等于400
0.85
3.为鼓励居民节约用电,某省试行阶段电价收费制,具体执行方案如表:
例如:一户居民七月份用电420度,则需缴电费420×0.85=357(元).
某户居民五、六月份共用电500度,缴电费290.5元.已知该用户六月份用电量大于五月份,且五、六月份的用电量均小于400度.问该户居民五、六月份各用电多少度?
解析:某户居民五、六月份共用电500度,就可以得出
每月用电量不可能都在第一档,分情况讨论,当5月份
用电量为x度≤200度,6月份用电(500-x)度,
当5月份用电量为x度>200度,六月份用电量为
(500-x)度,分别建立方程求出其解即可.
解:当5月份用电量为x度≤200度,6月份用电(500-x)度,由题意得
0.55x+0.6×(500-x)=290.5,
解得x=190,
∴6月份用电500-x=310(度).
当5月份用电量为x度>200度,六月份用电量为(500-x)度>200度,由题意得
0.6x+0.6×(500-x)=290.5,
方程无解,
∴该情况不符合题意.
答:该户居民五、六月份分别用电190度、310度.
课堂小结
1.
解决电话计费问题需要明确“哪种计费方式更省
钱”与“主叫时间”有关.
2.
此类问题的关键是能够根据已知条件找到合适
的分段点,然后建立方程模型分类讨论,从而
得出整体选择方案.
