人教版八年级数学上册第十一章11.1.1 三角形的边课件(23张ppt)
文档属性
| 名称 | 人教版八年级数学上册第十一章11.1.1 三角形的边课件(23张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-23 00:00:00 | ||
图片预览





文档简介
(共23张PPT)
11.1
与三角形有关的线段
11.1.1
三角形的边
教学目标
1、通过观察、操作、想象、推理、交流等活动,发掌空间观念、推理能力和有条理地表达能力;
2、结合具体实例,进一步认识三角形的概念及其基本要素,掌握三角形三边之间的不等关系.
探究新知:
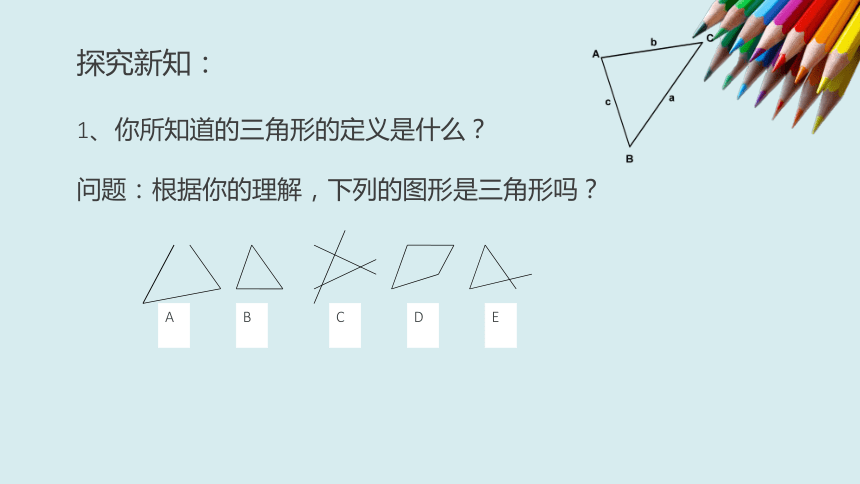
1、你所知道的三角形的定义是什么?
问题:根据你的理解,下列的图形是三角形吗?
A
B
D
C
E
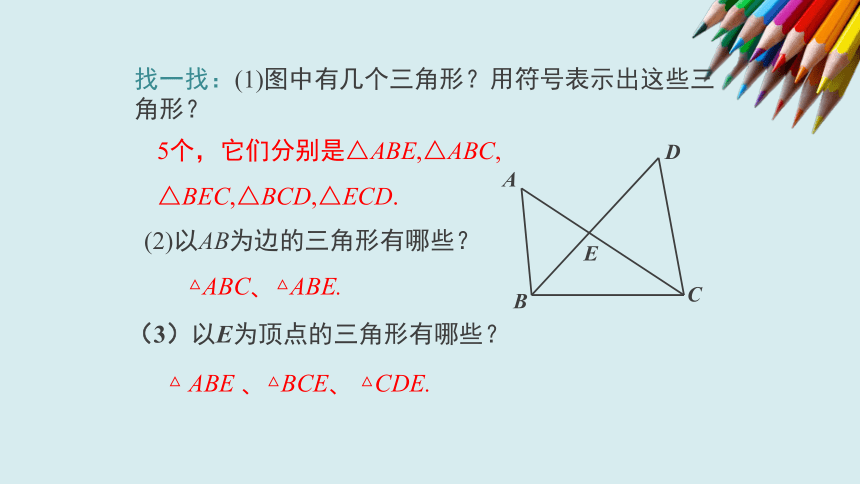
5个,它们分别是△ABE,△ABC,
△BEC,△BCD,△ECD.
找一找:(1)图中有几个三角形?用符号表示出这些三角形?
A
B
C
D
E
(2)以AB为边的三角形有哪些?
△ABC、△ABE.
(3)以E为顶点的三角形有哪些?
△
ABE
、△BCE、
△CDE.
(4)以∠D为角的三角形有哪些?
△
BCD、
△DEC.
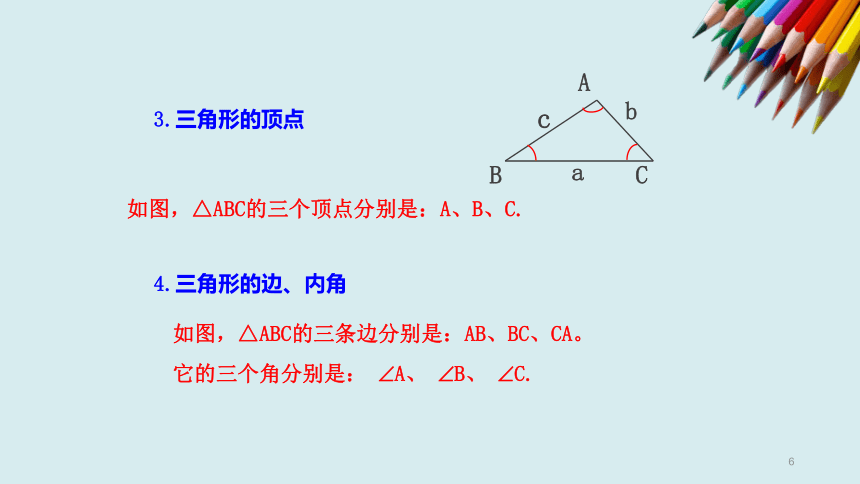
(5)说出△BCD的三个角和三个顶点所对的边.
△BCD的三个角是∠BCD、∠BDC、∠CBD.顶点B所对应的边为DC,顶点C所对应的边为BD,顶点D所对应的边为BC.
A
B
C
D
E
三角形的分类
问题1:观察下列三角形,说一说,按照三角形内角的大小,三角形可以分为哪几类?
锐角三角形、
直角三角形、
钝角三角形.
腰
不等边三角形
等腰三角形
等边三角形
底边
顶角
底角
问题2:你能找出下列三角形各自的特点吗?
三边均不相等
有两条边相等
三条边均相等
例1
有两根长度分别为5cm和8cm的木棒,用长度
为2cm的木棒与它们能摆成三角形吗?为什么?长
度为13cm的木棒呢?
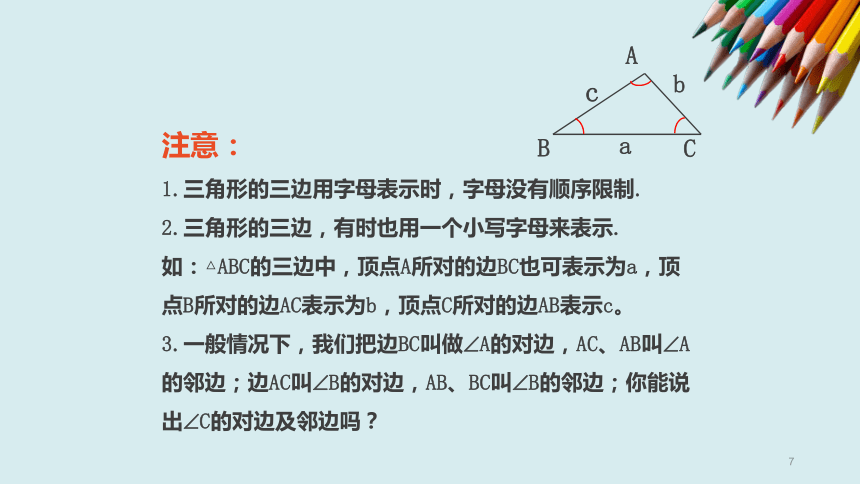
判断三条线段是否可以组成三角形,只需
说明两条较短线段之和大于第三条线段即可.
解:取长度为2cm的木棒时,由于2+5=7<8,出现了两边之和小于第三边的情况,所以它们不能摆成三角形.取长度为13cm的木棒时,由于5+8=13,出现了两边之和等于第三边的情况,所以它们也不能摆成三角形.
归纳
学以致用
例2
一个三角形的三边长分别为4,7,x,那么
x的取值范围是( )
A.3<x<11
B.4<x<7
C.-3<x<11
D.x>3
判断三角形边的取值范围要同时运用两边
之和大于第三边,两边之差小于第三边.
归纳
解析:∵三角形的三边长分别为4,7,x,∴7-4<x<7+4,即3<x<11.
A
1.下列长度的三条线段能否组成三角形?为什么?
(1)
3,4,8
(
)
(2)
2,5,6
(
)
(3)
5,6,10
(
)
(4)
3,5,8
(
)
不能
能
能
不能
课堂检测
4.如果等腰三角形的一边长是4cm,另一边长是9cm,则这个等腰三角形的周长为______________.
3.如果等腰三角形的一边长是5cm,另一边长是8cm,则这个等腰三角形的周长为______________.
2.五条线段的长分别为1cm,2cm,3cm,4cm,5cm,以其中三条线为边长可以构成________个三角形.
3
22cm
18cm或21cm
课堂小结
三角形概念
三角形分类
三角形三边关系
三角形表示方法
11.1
与三角形有关的线段
11.1.1
三角形的边
教学目标
1、通过观察、操作、想象、推理、交流等活动,发掌空间观念、推理能力和有条理地表达能力;
2、结合具体实例,进一步认识三角形的概念及其基本要素,掌握三角形三边之间的不等关系.
探究新知:
1、你所知道的三角形的定义是什么?
问题:根据你的理解,下列的图形是三角形吗?
A
B
D
C
E
5个,它们分别是△ABE,△ABC,
△BEC,△BCD,△ECD.
找一找:(1)图中有几个三角形?用符号表示出这些三角形?
A
B
C
D
E
(2)以AB为边的三角形有哪些?
△ABC、△ABE.
(3)以E为顶点的三角形有哪些?
△
ABE
、△BCE、
△CDE.
(4)以∠D为角的三角形有哪些?
△
BCD、
△DEC.
(5)说出△BCD的三个角和三个顶点所对的边.
△BCD的三个角是∠BCD、∠BDC、∠CBD.顶点B所对应的边为DC,顶点C所对应的边为BD,顶点D所对应的边为BC.
A
B
C
D
E
三角形的分类
问题1:观察下列三角形,说一说,按照三角形内角的大小,三角形可以分为哪几类?
锐角三角形、
直角三角形、
钝角三角形.
腰
不等边三角形
等腰三角形
等边三角形
底边
顶角
底角
问题2:你能找出下列三角形各自的特点吗?
三边均不相等
有两条边相等
三条边均相等
例1
有两根长度分别为5cm和8cm的木棒,用长度
为2cm的木棒与它们能摆成三角形吗?为什么?长
度为13cm的木棒呢?
判断三条线段是否可以组成三角形,只需
说明两条较短线段之和大于第三条线段即可.
解:取长度为2cm的木棒时,由于2+5=7<8,出现了两边之和小于第三边的情况,所以它们不能摆成三角形.取长度为13cm的木棒时,由于5+8=13,出现了两边之和等于第三边的情况,所以它们也不能摆成三角形.
归纳
学以致用
例2
一个三角形的三边长分别为4,7,x,那么
x的取值范围是( )
A.3<x<11
B.4<x<7
C.-3<x<11
D.x>3
判断三角形边的取值范围要同时运用两边
之和大于第三边,两边之差小于第三边.
归纳
解析:∵三角形的三边长分别为4,7,x,∴7-4<x<7+4,即3<x<11.
A
1.下列长度的三条线段能否组成三角形?为什么?
(1)
3,4,8
(
)
(2)
2,5,6
(
)
(3)
5,6,10
(
)
(4)
3,5,8
(
)
不能
能
能
不能
课堂检测
4.如果等腰三角形的一边长是4cm,另一边长是9cm,则这个等腰三角形的周长为______________.
3.如果等腰三角形的一边长是5cm,另一边长是8cm,则这个等腰三角形的周长为______________.
2.五条线段的长分别为1cm,2cm,3cm,4cm,5cm,以其中三条线为边长可以构成________个三角形.
3
22cm
18cm或21cm
课堂小结
三角形概念
三角形分类
三角形三边关系
三角形表示方法
