2020-2021学年山东省潍坊市奎文区等六区联考九年级(上)期末数学试卷(word解析版)
文档属性
| 名称 | 2020-2021学年山东省潍坊市奎文区等六区联考九年级(上)期末数学试卷(word解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-22 21:49:32 | ||
图片预览


文档简介
2020-2021学年山东省潍坊市奎文区等六区联考九年级第一学期期末数学试卷
一、单选题(共8小题,共24分.)
1.函数y=中,自变量x的取值范围是( )
A.x>1
B.x≥1
C.x<1
D.x≤1
2.下列说法正确的是( )
A.“概率为0.0001的事件”是不可能事件
B.任意掷一枚质地均匀的硬币10次,正面向上的一定是5次
C.“任意画出一个等边三角形,它是轴对称图形”是随机事件
D.“任意画出一个平行四边形,它是中心对称图形”是必然事件
3.如图,⊙O的半径为3,AB为弦,若∠ABC=30°,则的长为( )
A.π
B.1
C.1.5
D.1.5π
4.若关于x的方程(m+1)x2﹣2x﹣1=0有实数根,则m的取值范围是( )
A.m>﹣2
B.m≥﹣2
C.m>﹣2且m≠﹣1
D.m≥﹣2且m≠﹣1
5.点P1(﹣0.5,y1),P2(2.5,y2),P3(﹣5,y3)均在二次函数y=﹣x2+2x的图象上,则y1,y2,y3的大小关系是( )
A.y3>y2>y1
B.y3>y1=y2
C.y1>y2>y3
D.y1=y2>y3
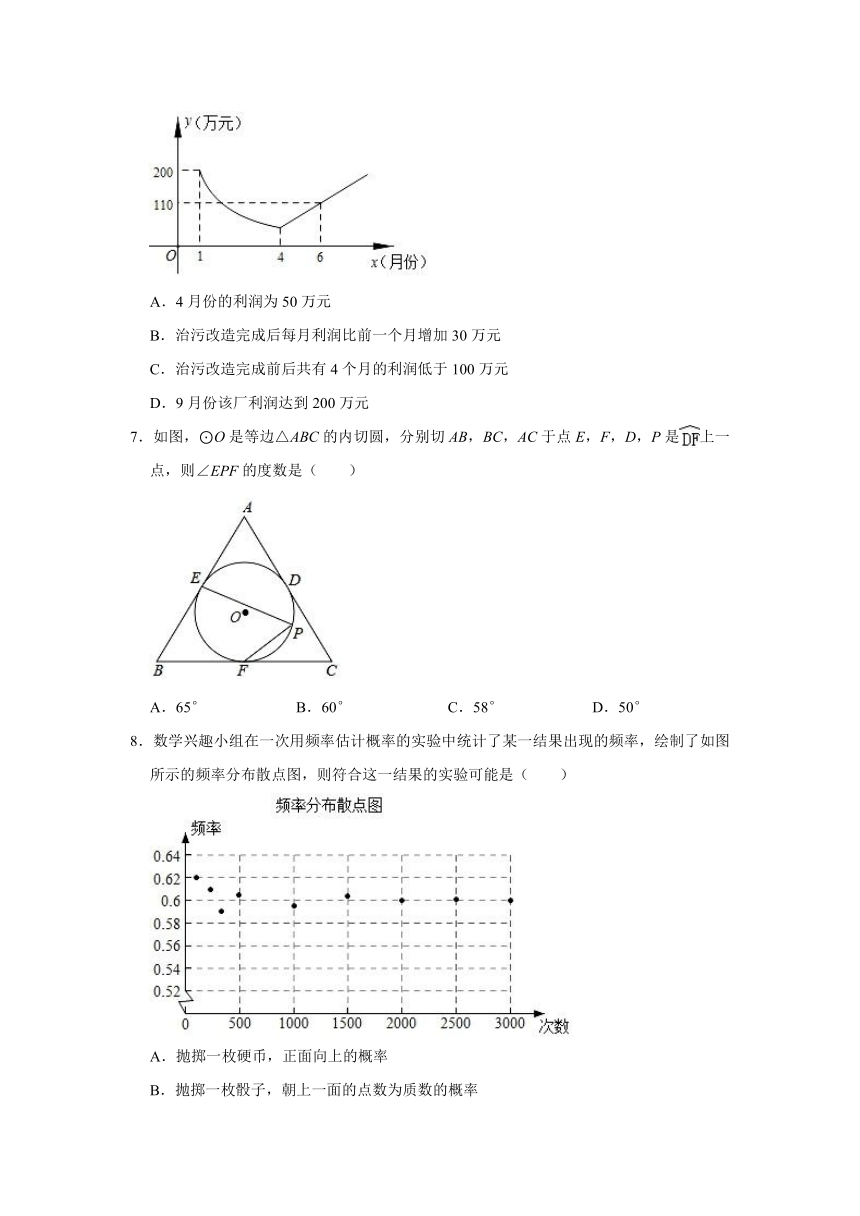
6.为了响应“绿水青山就是金山银山”的号召,建设生态文明,某工厂自2019年1月开始限产进行治污改造,其月利润y(万元)与月份x之间的变化如图所示,治污完成前是反比例函数图象的一部分,治污完成后是一次函数图象的一部分,下列选项错误的是( )
A.4月份的利润为50万元
B.治污改造完成后每月利润比前一个月增加30万元
C.治污改造完成前后共有4个月的利润低于100万元
D.9月份该厂利润达到200万元
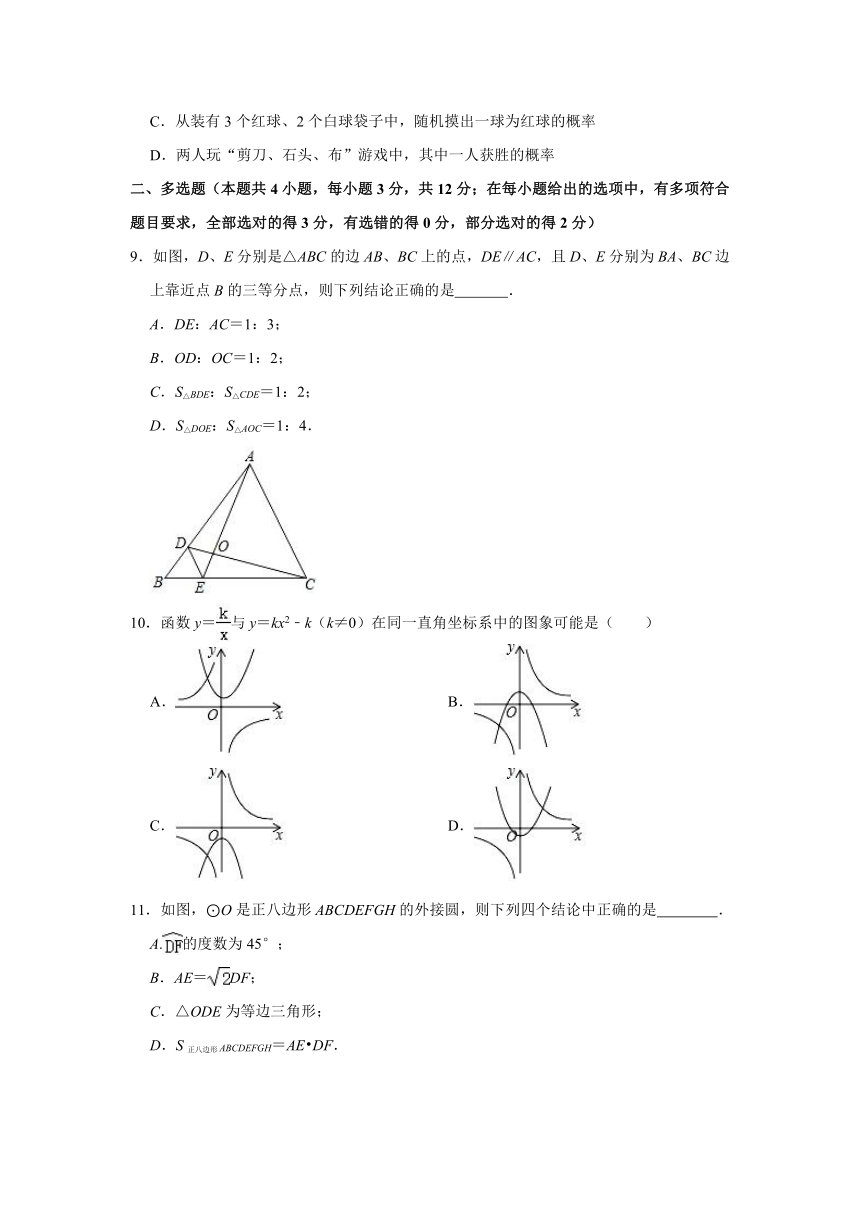
7.如图,⊙O是等边△ABC的内切圆,分别切AB,BC,AC于点E,F,D,P是上一点,则∠EPF的度数是( )
A.65°
B.60°
C.58°
D.50°
8.数学兴趣小组在一次用频率估计概率的实验中统计了某一结果出现的频率,绘制了如图所示的频率分布散点图,则符合这一结果的实验可能是( )
A.抛掷一枚硬币,正面向上的概率
B.抛掷一枚骰子,朝上一面的点数为质数的概率
C.从装有3个红球、2个白球袋子中,随机摸出一球为红球的概率
D.两人玩“剪刀、石头、布”游戏中,其中一人获胜的概率
二、多选题(本题共4小题,每小题3分,共12分;在每小题给出的选项中,有多项符合题目要求,全部选对的得3分,有选错的得0分,部分选对的得2分)
9.如图,D、E分别是△ABC的边AB、BC上的点,DE∥AC,且D、E分别为BA、BC边上靠近点B的三等分点,则下列结论正确的是
.
A.DE:AC=1:3;
B.OD:OC=1:2;
C.S△BDE:S△CDE=1:2;
D.S△DOE:S△AOC=1:4.
10.函数y=与y=kx2﹣k(k≠0)在同一直角坐标系中的图象可能是( )
A.
B.
C.
D.
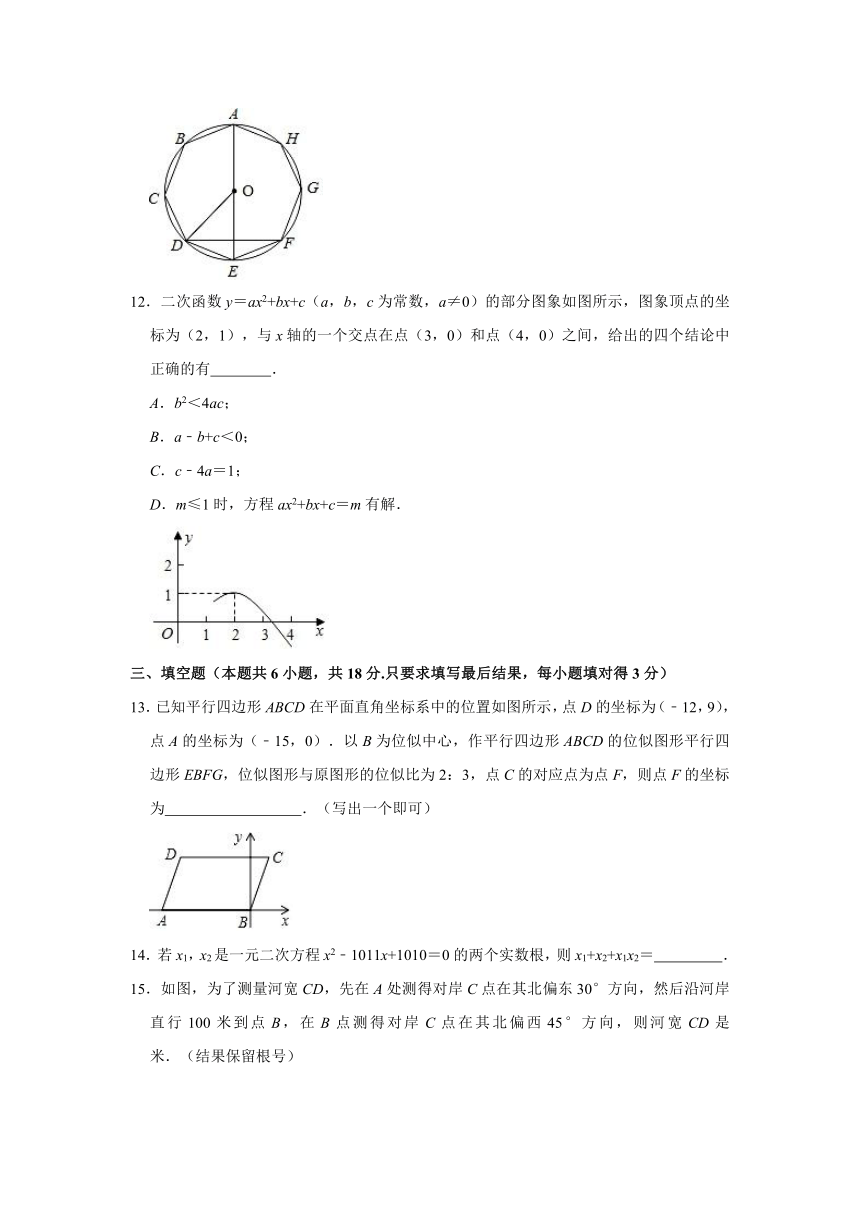
11.如图,⊙O是正八边形ABCDEFGH的外接圆,则下列四个结论中正确的是
.
A.的度数为45°;
B.AE=DF;
C.△ODE为等边三角形;
D.S正八边形ABCDEFGH=AE?DF.
12.二次函数y=ax2+bx+c(a,b,c为常数,a≠0)的部分图象如图所示,图象顶点的坐标为(2,1),与x轴的一个交点在点(3,0)和点(4,0)之间,给出的四个结论中正确的有
.
A.b2<4ac;
B.a﹣b+c<0;
C.c﹣4a=1;
D.m≤1时,方程ax2+bx+c=m有解.
三、填空题(本题共6小题,共18分.只要求填写最后结果,每小题填对得3分)
13.已知平行四边形ABCD在平面直角坐标系中的位置如图所示,点D的坐标为(﹣12,9),点A的坐标为(﹣15,0).以B为位似中心,作平行四边形ABCD的位似图形平行四边形EBFG,位似图形与原图形的位似比为2:3,点C的对应点为点F,则点F的坐标为
.(写出一个即可)
14.若x1,x2是一元二次方程x2﹣1011x+1010=0的两个实数根,则x1+x2+x1x2=
.
15.如图,为了测量河宽CD,先在A处测得对岸C点在其北偏东30°方向,然后沿河岸直行100米到点B,在B点测得对岸C点在其北偏西45°方向,则河宽CD是
米.(结果保留根号)
16.正方形ABCD的边长为2,以各边为直径在正方形内画半圆,得到如图所示阴影部分,若随机向正方形ABCD内投一粒米,则米粒落在阴影部分的概率为
.
17.如图,A、B分别是反比例函数y=(x>0)图象上的两点,连接OA,OB,分别过点A、B作x轴的垂线,垂足分别为C、E,且AC交OB于点D,若AD=CD,则的值为
.
18.如图,AB、CD是半径为5的⊙O的两条弦,AB=8,CD=6,MN是直径,AB⊥MN于点E,CD⊥MN于点F,P为EF上的任意一点,则PA+PC的最小值为
.
四、解答题(本题共7小题,共66分.解答应写出文字说明、证明过程或推演步骤)
19.已知二次函数y=x2﹣4x+m(m为常数).
(1)若其图象与x轴有两个交点,求m的取值范围;
(2)求其图象与直线y=m+5交点的横坐标.
20.某市为了解八年级学生数数学学习状况,以2.5%的比例随机抽取了八年级部分学生进行了数学测试(满分100分),测试后将成绩绘制成两幅不完整的统计图表,如下图表所示,测试成绩中没有满分和低于20分的成绩.请根据统计图表中的信息解决下列问题:
八年级数学频数、频率分布表
分数段
频数
频率
90≤x<100
2
0.008
80≤x<90
8
0.032
70≤x<80
a
n
60≤x<70
85
0.340
50≤x<60
b
0.260
40≤x<50
48
0.192
30≤x<40
5
0.020
20≤x<30
2
0.008
(1)直接写出表中a,b的值,并补全频数分布直方图;
(2)若把成绩在80≤x<100范围内的学生视为数学“特长生”,估计该市八年级学生中有多少名数学“特长生”?
(3)在“90≤x<100”和“20≤x<30”分数段的4名同学中,男女各有2名,现从中随机选取两人进行座谈,请用列表或画树状图的方法求出恰好选中一男一女的概率.
21.如图,一次函数y=mx+b与反比例函数y=的图象交于A,B两点,OB=,且点B的横坐标是该点纵坐标的2倍.该一次函数与y轴交于点C,与x轴交于点D.
(1)求点B的坐标及一次函数的解析式;
(2)求△ABO的面积S;
(3)直接写出不等式mx+b≥的解集.
22.如图,矩形EFGH内接于△ABC(矩形各顶点在三角形边上),E,F在BC上,H,G分别在AB,AC上,且AD⊥BC于点D,交HG于点N.
(1)求证:△AHG∽△ABC;
(2)若AD=3,BC=9,设EH=x,矩形EFGH的面积为y,求出y与x之间的函数表达式,并写出自变量x的取值范围.
23.某公司推出一款电子产品,经市场调查发现,该产品的日销售量y(个)与销售单价x(元/个)之间满足一次函数关系.销售单价、日销售量、日销售利润的几组对应值如表:
销售单价x(元/个)
60
65
70
75
日销售量y(个)
180
130
80
30
日销售利润w(元)
1800
1950
1600
750
注:日销售利润=日销售量×(销售单价﹣成本单价)
(1)求y关于x的函数表达式;
(2)该产品的成本价是
元/个,求日销售利润w的最大值;
(3)直接写出单价x满足什么条件时,销售利润不低于1920元.
24.如图,已知Rt△ABC中,∠ACB=90°,AD平分∠BAC,交BC于点D,以AB上某一点O为圆心作⊙O使⊙O经过点A和点D,交AB于点E,连接ED并延长交AC的延长线于点F.
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若AE=12,CF=3,求BE的长;
(3)在(2)的条件下,求阴影区域的面积.
25.如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c经过A(﹣3,0)、B(1,0)两点,与y轴交于点C,连接BC.点P是位于x轴上方抛物线上的一个动点,过P作PE⊥x轴,垂足为点E.
(1)求抛物线的函数表达式;
(2)是否存在点P,使得以A、P、E为顶点的三角形与△BOC相似?若存在,求出点P的坐标;若不存在,说明理由;
(3)是否存在点P,使得四边形ABCP的面积最大?若存在,请求出点P的坐标;若不存在,请说明理由.
参考答案
一、单选题(本题共8小题,共24分.在每个小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来,每小题选对得3分,错选、不选或选出的答案超过一个均记0分)
1.函数y=中,自变量x的取值范围是( )
A.x>1
B.x≥1
C.x<1
D.x≤1
解:由题意得,x﹣1≥0,
解得x≥1.
故选:B.
2.下列说法正确的是( )
A.“概率为0.0001的事件”是不可能事件
B.任意掷一枚质地均匀的硬币10次,正面向上的一定是5次
C.“任意画出一个等边三角形,它是轴对称图形”是随机事件
D.“任意画出一个平行四边形,它是中心对称图形”是必然事件
解:A、“概率为0.0001的事件”是随机事件,选项错误;
B、任意掷一枚质地均匀的硬币10次,正面向上的可能是5次,选项错误;
C、“任意画出一个等边三角形,它是轴对称图形”是必然事件,选项错误;
D、“任意画出一个平行四边形,它是中心对称图形”是必然事件,选项正确;
故选:D.
3.如图,⊙O的半径为3,AB为弦,若∠ABC=30°,则的长为( )
A.π
B.1
C.1.5
D.1.5π
解:
连接OA、OC,
∵∠ABC=30°,
∴∠AOC=2∠ABC=60°,
∵⊙O的半径为3,
∴的长为=π,
故选:A.
4.若关于x的方程(m+1)x2﹣2x﹣1=0有实数根,则m的取值范围是( )
A.m>﹣2
B.m≥﹣2
C.m>﹣2且m≠﹣1
D.m≥﹣2且m≠﹣1
解:当m+1=0时,即m=﹣1时,此时方程为﹣2x﹣1=0,该方程有解,此时m=﹣1;
当m+1≠0时,则方程(m+1)x2﹣2x﹣1=0为一元二次方程,其判别式为Δ=(﹣2)2﹣4(m+1)×(﹣1)=8+4m,
∵方程(m+1)x2﹣2x﹣1=0有实数根,
∴8+4m≥0,解得m≥﹣2;
此时m的取值范围是m≥﹣2且m≠﹣1;
综上可知m的取值范围是m≥﹣2,
故选:B.
5.点P1(﹣0.5,y1),P2(2.5,y2),P3(﹣5,y3)均在二次函数y=﹣x2+2x的图象上,则y1,y2,y3的大小关系是( )
A.y3>y2>y1
B.y3>y1=y2
C.y1>y2>y3
D.y1=y2>y3
解:∵y=﹣x2+2x=﹣(x﹣1)2+1,
∴抛物线对称轴为直线x=1,
∵a=﹣1<0,
∴x<1时,y随x的增大而增大,
∵P2(2.5,y2)的对称点为(﹣0.5,y2),且﹣5<﹣0.5<1,
∴y1=y2>y3.
故选:D.
6.为了响应“绿水青山就是金山银山”的号召,建设生态文明,某工厂自2019年1月开始限产进行治污改造,其月利润y(万元)与月份x之间的变化如图所示,治污完成前是反比例函数图象的一部分,治污完成后是一次函数图象的一部分,下列选项错误的是( )
A.4月份的利润为50万元
B.治污改造完成后每月利润比前一个月增加30万元
C.治污改造完成前后共有4个月的利润低于100万元
D.9月份该厂利润达到200万元
解:A、设反比例函数的解析式为y=,
把(1,200)代入得,k=200,
∴反比例函数的解析式为:y=,
当x=4时,y=50,
∴4月份的利润为50万元,故此选项正确,不合题意;
B、治污改造完成后,从4月到6月,利润从50万到110万,故每月利润比前一个月增加30万元,故此选项正确,不合题意;
C、当y=100时,则100=,
解得:x=2,
则只有3月,4月,5月共3个月的利润低于100万元,故此选项不正确,符合题意.
D、设一次函数解析式为:y=kx+b,
则,
解得:,
故一次函数解析式为:y=30x﹣70,
故y=200时,200=30x﹣70,
解得:x=9,
则治污改造完成后的第5个月,即9月份该厂利润达到200万元,故此选项正确,不合题意.
故选:C.
7.如图,⊙O是等边△ABC的内切圆,分别切AB,BC,AC于点E,F,D,P是上一点,则∠EPF的度数是( )
A.65°
B.60°
C.58°
D.50°
解:如图,连接OE,OF.
∵⊙O是△ABC的内切圆,E,F是切点,
∴OE⊥AB,OF⊥BC,
∴∠OEB=∠OFB=90°,
∵△ABC是等边三角形,
∴∠B=60°,
∴∠EOF=120°,
∴∠EPF=∠EOF=60°,
故选:B.
8.数学兴趣小组在一次用频率估计概率的实验中统计了某一结果出现的频率,绘制了如图所示的频率分布散点图,则符合这一结果的实验可能是( )
A.抛掷一枚硬币,正面向上的概率
B.抛掷一枚骰子,朝上一面的点数为质数的概率
C.从装有3个红球、2个白球袋子中,随机摸出一球为红球的概率
D.两人玩“剪刀、石头、布”游戏中,其中一人获胜的概率
解:A、掷一枚硬币,出现正面朝上的概率为,故此选项不符合题意;
B、抛掷一枚骰子,朝上一面的点数为质数的概率为=,故此选项不符合题意;
C.从装有3个红球、2个白球袋子中,随机摸出一球为红球的概率为=,故此选项符合题意;
D.两人玩“剪刀、石头、布”游戏中,其中一人获胜的概率为=,故此选项不符合题意;
故选:C.
二、多选题(本题共4小题,每小题3分,共12分;在每小题给出的选项中,有多项符合题目要求,全部选对的得3分,有选错的得0分,部分选对的得2分)
9.如图,D、E分别是△ABC的边AB、BC上的点,DE∥AC,且D、E分别为BA、BC边上靠近点B的三等分点,则下列结论正确的是 AC .
A.DE:AC=1:3;
B.OD:OC=1:2;
C.S△BDE:S△CDE=1:2;
D.S△DOE:S△AOC=1:4.
解:∵DE∥AC,
∴△BDE∽△BAC,△ODE∽△OCA,
∴,,
∵D、E分别为BA、BC边上靠近点B的三等分点,
∴DE:AC=1:3,OD:OC=1:3,S△BDE:S△CDE=1:2,
∴S△DOE:S△AOC=1:9.
故答案为:AC.
10.函数y=与y=kx2﹣k(k≠0)在同一直角坐标系中的图象可能是( )
A.
B.
C.
D.
解:分两种情况讨论:
①当k<0时,反比例函数y=,在二、四象限,而二次函数y=kx2﹣k开口向下,故A、B、C、D都不符合题意;
②当k>0时,反比例函数y=,在一、三象限,而二次函数y=kx2﹣k开口向上,与y轴交点在原点下方,故选项D正确,
故选:D.
11.如图,⊙O是正八边形ABCDEFGH的外接圆,则下列四个结论中正确的是 B,D .
A.的度数为45°;
B.AE=DF;
C.△ODE为等边三角形;
D.S正八边形ABCDEFGH=AE?DF.
解:连接OF,
∵∠DOE=∠EOF==45°,
∴∠DOF=90°,
∴弧DF的度数为90°,
∴A错误;
∵∠DOF=90°,OD=OF,
∴2OD2=DF2,
∴OD=DF,
∵AE=2OD,
∴AE=DF,
∴B正确;
∵∠DOE=45°,
∴C错误;
∵S四边形ODEF=DF?OE,
∴S正八边形ABCDEFGH=4S四边形ODEF=2DF?OE,
∵OE=AE,
∴S正八边形ABCDEFGH=AE?DF,
∴D正确;
故答案为:B,D.
12.二次函数y=ax2+bx+c(a,b,c为常数,a≠0)的部分图象如图所示,图象顶点的坐标为(2,1),与x轴的一个交点在点(3,0)和点(4,0)之间,给出的四个结论中正确的有 BCD .
A.b2<4ac;
B.a﹣b+c<0;
C.c﹣4a=1;
D.m≤1时,方程ax2+bx+c=m有解.
解:由图象可知,抛物线开口向下,对称轴在y轴的右侧,与y轴的交点在y轴的负半轴,
∵抛物线与x轴有两个交点,
∴Δ>0,
∴b2﹣4ac>0,即b2>4ac,故A错误;
由图象可知,x=﹣1时,y<0,
∴a﹣b+c<0,故B正确;
∵抛物线的顶点坐标为(2,1),
∴﹣=2,b=﹣4a,
∵4a+2b+c=1,
∴4a﹣8a+c=1,即c﹣4a=1,故C正确;
∵抛物线的开口向下,顶点坐标为(2,1),
∴am2+bm+c≤1(m为任意实数),即m≤1时,方程ax2+bx+c=m有解.故D正确.
故答案为:BCD.
三、填空题(本题共6小题,共18分.只要求填写最后结果,每小题填对得3分)
13.已知平行四边形ABCD在平面直角坐标系中的位置如图所示,点D的坐标为(﹣12,9),点A的坐标为(﹣15,0).以B为位似中心,作平行四边形ABCD的位似图形平行四边形EBFG,位似图形与原图形的位似比为2:3,点C的对应点为点F,则点F的坐标为 (﹣2,﹣6)或(2,6) .(写出一个即可)
解:∵平行四边形ABCD,点D的坐标为(﹣12,9),点A的坐标为(﹣15,0),
∴C(3,9),
∵以B为位似中心,点C的对应点为点F,位似图形与原图形的位似比为2:3,
∴点F的坐标为:(3×,9×)或[3×(﹣),9×(﹣)]即(﹣2,﹣6)或(2,6).
故答案为:(﹣2,﹣6)或(2,6).
14.若x1,x2是一元二次方程x2﹣1011x+1010=0的两个实数根,则x1+x2+x1x2= 2021 .
解:∵若x1,x2是一元二次方程x2﹣1011x+1010=0的两个实数根,
∴x1+x2=1011,x1?x2=1010,
∴x1+x2+x1x2=1011+1010=2021.
故答案是:2021.
15.如图,为了测量河宽CD,先在A处测得对岸C点在其北偏东30°方向,然后沿河岸直行100米到点B,在B点测得对岸C点在其北偏西45°方向,则河宽CD是 (150﹣50) 米.(结果保留根号)
解:设CD=x米,
由题意得:CD⊥AB,∠ACD=30°,∠BCD=45°,
∴∠ADC=∠BDC=90°,
∴AD=CD=x米,BD=CD=x米,
∵AD+BD=AB=100米,
∴x+x=100,
解得:x=150﹣50,
即河宽CD是(150﹣50)米,
故答案为:(150﹣50).
16.正方形ABCD的边长为2,以各边为直径在正方形内画半圆,得到如图所示阴影部分,若随机向正方形ABCD内投一粒米,则米粒落在阴影部分的概率为 .
解:正方形的面积为2×2=4,
阴影部分的面积为:4S半圆﹣S正方形=4××π×12﹣4=2π﹣4,
∴P米粒落在阴影部分的概率==,
故答案为:.
17.如图,A、B分别是反比例函数y=(x>0)图象上的两点,连接OA,OB,分别过点A、B作x轴的垂线,垂足分别为C、E,且AC交OB于点D,若AD=CD,则的值为 .
解:设A(a,),a>0,
∵AD=CD且AD⊥x轴,
∴D(a,),
设直线OD的解析式为:y=kx,将D点代入得:
k=,
∴直线OD的解析式为:y=x,
∵B点为直线OD与反比例函数的交点,
∴联立方程得:,
解得:x=﹣(舍去),x=,
∴BE=,CD=,
∴==,
故答案为:.
18.如图,AB、CD是半径为5的⊙O的两条弦,AB=8,CD=6,MN是直径,AB⊥MN于点E,CD⊥MN于点F,P为EF上的任意一点,则PA+PC的最小值为 .
解:连接OB,OC,作CH垂直AB于H.
根据垂径定理,得到BE=AB=4,CF=CD=3,
∴OE===3,
OF===4,
∴CH=OE+OF=3+4=7,
BH=BE+EH=BE+CF=4+3=7,
在直角△BCH中根据勾股定理得到BC=7,
则PA+PC的最小值为.
故答案为:
四、解答题(本题共7小题,共66分.解答应写出文字说明、证明过程或推演步骤)
19.已知二次函数y=x2﹣4x+m(m为常数).
(1)若其图象与x轴有两个交点,求m的取值范围;
(2)求其图象与直线y=m+5交点的横坐标.
解:(1)根据题意得,Δ=b2﹣4ac=16﹣4m>0,
∴m<4;
(2)根据题意得,x2﹣4x+m=m+5,
解得,x1=5,x2=﹣1,
∴图象与直线y=m+5交点的横坐标为5或﹣1.
20.某市为了解八年级学生数数学学习状况,以2.5%的比例随机抽取了八年级部分学生进行了数学测试(满分100分),测试后将成绩绘制成两幅不完整的统计图表,如下图表所示,测试成绩中没有满分和低于20分的成绩.请根据统计图表中的信息解决下列问题:
八年级数学频数、频率分布表
分数段
频数
频率
90≤x<100
2
0.008
80≤x<90
8
0.032
70≤x<80
a
n
60≤x<70
85
0.340
50≤x<60
b
0.260
40≤x<50
48
0.192
30≤x<40
5
0.020
20≤x<30
2
0.008
(1)直接写出表中a,b的值,并补全频数分布直方图;
(2)若把成绩在80≤x<100范围内的学生视为数学“特长生”,估计该市八年级学生中有多少名数学“特长生”?
(3)在“90≤x<100”和“20≤x<30”分数段的4名同学中,男女各有2名,现从中随机选取两人进行座谈,请用列表或画树状图的方法求出恰好选中一男一女的概率.
解:(1)n=1﹣(0.008+0.032+0.260+0.340+0.192+0.020+0.008)=0.14,
抽取的总人数为:2÷0.008=250(人),
a=250×0.14=35(人),
b=250×0.260=65(人).
补全统计图如下:
(2)250÷2.5%×(0.008+0.032)=400(人),
答:该市八年级学生中有400名数学“特长生”.
(3)用A、B表示两名男生,用C、D表示两名女生,画树状图如图:
共有12种等可能的情况,恰好一男一女的种类有8种
所以恰好选中一男一女的概率是=.
21.如图,一次函数y=mx+b与反比例函数y=的图象交于A,B两点,OB=,且点B的横坐标是该点纵坐标的2倍.该一次函数与y轴交于点C,与x轴交于点D.
(1)求点B的坐标及一次函数的解析式;
(2)求△ABO的面积S;
(3)直接写出不等式mx+b≥的解集.
解:(1)如图,过点B作BH⊥x轴于点H,在△OBH中,设BH=x,OB=2x,
∴x2+(2x)2=5,
∴x=1,
∴点B的坐标为(﹣2,﹣1),
∴把(﹣2,﹣1)代入y=得,m=2,
设一次函数的解析式为:y=2x+b,把(﹣2,﹣1)代入得:b=3,
∴一次函数的解析式为y=2x+3;
(2)由得点A坐标为,
由直线y=2x+3可知,点C坐标为(0,3),OC=3,
∵S△AOB=S△AOC+S△BOC,
∴;
(3)由图象可知,不等式mx+b≥的解集为.
22.如图,矩形EFGH内接于△ABC(矩形各顶点在三角形边上),E,F在BC上,H,G分别在AB,AC上,且AD⊥BC于点D,交HG于点N.
(1)求证:△AHG∽△ABC;
(2)若AD=3,BC=9,设EH=x,矩形EFGH的面积为y,求出y与x之间的函数表达式,并写出自变量x的取值范围.
解:(1)证明:∵四边形EFGH是矩形,
∵HG∥BC,
∴,
∵∠HAG=∠BAC,
∴△AHG∽△ABC,
(2)解:∵四边形EFGH是矩形,
∴∠HED=∠EHN=90°,
∵AD⊥BC,
∴四边形HEDN是矩形,EH=x,
∴ND=EH=x,
∵AD=3,
∴AN=3﹣x,
∵△AHG∽△ABC,
∴,
∴,
∴HG=9﹣3x,
∵矩形EFGH的面积=HG?HE
∴y=x(9﹣3x)=﹣3x2+9x(0<x<3).
23.某公司推出一款电子产品,经市场调查发现,该产品的日销售量y(个)与销售单价x(元/个)之间满足一次函数关系.销售单价、日销售量、日销售利润的几组对应值如表:
销售单价x(元/个)
60
65
70
75
日销售量y(个)
180
130
80
30
日销售利润w(元)
1800
1950
1600
750
注:日销售利润=日销售量×(销售单价﹣成本单价)
(1)求y关于x的函数表达式;
(2)该产品的成本价是 50 元/个,求日销售利润w的最大值;
(3)直接写出单价x满足什么条件时,销售利润不低于1920元.
解:(1)设y关于x的函数表达式为y=kx+b,
把(60,180),(65,130)代入得:
,
解得:,
∴y关于x的函数表达式为y=﹣10x+780;
(2)由表中数据知,当x=60时,y=180,w=1800,
∴该产品的成本价为60﹣1800÷180=50(元/个),
故答案为:50;
根据题意得,w=(x﹣50)(﹣10x+780)
∴w=10x2+1280x﹣39000=﹣10(x﹣64)2+1960
∴当x=64时,w最大为1960元;
(3)由题意得:﹣10(x﹣64)2+1960≥1920,
即﹣10(x﹣64)2≥﹣40,
解得:62≤x≤66,
∴当62≤x≤66时,销售利润不低于1920元.
24.如图,已知Rt△ABC中,∠ACB=90°,AD平分∠BAC,交BC于点D,以AB上某一点O为圆心作⊙O使⊙O经过点A和点D,交AB于点E,连接ED并延长交AC的延长线于点F.
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若AE=12,CF=3,求BE的长;
(3)在(2)的条件下,求阴影区域的面积.
【解答】(1)证明:直线BC与⊙O相切,理由如下:
如图,连接OD,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵OA=OD,
∴∠BAD=∠ODA,
∴∠ODA=∠CAD,
∴OD∥AC,
∵∠ACB=90°,
∵∠ODB=∠ACB=90°,
∴OD⊥BC,
∴BC是⊙O的切线;
(2)解:∵AE是⊙O直径,
∴∠ADE=90°,
∴AD⊥EF,
∵AD平分∠BAC,AE=12,
∴AE=AF=12,
∵CF=3,
∴AC=9,
在Rt△ADF中,∠ACD=90°,
∴∠FDC+∠ADC=∠CAD+∠ADC,
∴∠FDC=∠CAD,
∵∠DCF=∠ACD=90°,
∴△DCF∽△ACD,
∴=,
∴CD2=AC?CF,
∴,
∵tan∠CAD===,
∴∠CAD=30°,
∴∠BAD=30°,
∴∠B=90°﹣∠BAC=30°,
在Rt△ABC中,AC=9,
∴AB=18,
∴BE=18﹣12=6;
(3)解:∵OD⊥BC,∠B=30°,OD=AE=6,
∴,
∴,
∵∠BAD=30°,
∴∠BOD=60°,
∴S扇形EOD==6π,
∴.
25.如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c经过A(﹣3,0)、B(1,0)两点,与y轴交于点C,连接BC.点P是位于x轴上方抛物线上的一个动点,过P作PE⊥x轴,垂足为点E.
(1)求抛物线的函数表达式;
(2)是否存在点P,使得以A、P、E为顶点的三角形与△BOC相似?若存在,求出点P的坐标;若不存在,说明理由;
(3)是否存在点P,使得四边形ABCP的面积最大?若存在,请求出点P的坐标;若不存在,请说明理由.
解:(1)把A(﹣3,0)、B(1,0)代入y=﹣x2+bx+c得:
,
解得:,
∴抛物线的函数解析式为y=﹣x2﹣2x+3;
(2)∵A(﹣3,0),B(1,0),C(0,3),
∴OC=3,OB=1,
∴设P(m,﹣m2﹣2m+3),
∴PE=﹣m2﹣2m+3,AE=m+3,
根据题意得:,
解得:m1=﹣2,m2=﹣3(舍去),
∴P1(﹣2,3),
或,
解得:(舍去),
∴,
综上,点P坐标为P1(﹣2,3)或.
(3)连接AC交PE于点H,
由A(﹣3,0),C(0,3)得直线AC的表达式为:y=x+3,
设P(m,﹣m2﹣2m+3),则H(m,m+3),
∴PH=﹣m2﹣3m
∴
∴S四边形ABCP=S△PAC+S△ABC==
当时,,此时点P的坐标为(﹣,).
一、单选题(共8小题,共24分.)
1.函数y=中,自变量x的取值范围是( )
A.x>1
B.x≥1
C.x<1
D.x≤1
2.下列说法正确的是( )
A.“概率为0.0001的事件”是不可能事件
B.任意掷一枚质地均匀的硬币10次,正面向上的一定是5次
C.“任意画出一个等边三角形,它是轴对称图形”是随机事件
D.“任意画出一个平行四边形,它是中心对称图形”是必然事件
3.如图,⊙O的半径为3,AB为弦,若∠ABC=30°,则的长为( )
A.π
B.1
C.1.5
D.1.5π
4.若关于x的方程(m+1)x2﹣2x﹣1=0有实数根,则m的取值范围是( )
A.m>﹣2
B.m≥﹣2
C.m>﹣2且m≠﹣1
D.m≥﹣2且m≠﹣1
5.点P1(﹣0.5,y1),P2(2.5,y2),P3(﹣5,y3)均在二次函数y=﹣x2+2x的图象上,则y1,y2,y3的大小关系是( )
A.y3>y2>y1
B.y3>y1=y2
C.y1>y2>y3
D.y1=y2>y3
6.为了响应“绿水青山就是金山银山”的号召,建设生态文明,某工厂自2019年1月开始限产进行治污改造,其月利润y(万元)与月份x之间的变化如图所示,治污完成前是反比例函数图象的一部分,治污完成后是一次函数图象的一部分,下列选项错误的是( )
A.4月份的利润为50万元
B.治污改造完成后每月利润比前一个月增加30万元
C.治污改造完成前后共有4个月的利润低于100万元
D.9月份该厂利润达到200万元
7.如图,⊙O是等边△ABC的内切圆,分别切AB,BC,AC于点E,F,D,P是上一点,则∠EPF的度数是( )
A.65°
B.60°
C.58°
D.50°
8.数学兴趣小组在一次用频率估计概率的实验中统计了某一结果出现的频率,绘制了如图所示的频率分布散点图,则符合这一结果的实验可能是( )
A.抛掷一枚硬币,正面向上的概率
B.抛掷一枚骰子,朝上一面的点数为质数的概率
C.从装有3个红球、2个白球袋子中,随机摸出一球为红球的概率
D.两人玩“剪刀、石头、布”游戏中,其中一人获胜的概率
二、多选题(本题共4小题,每小题3分,共12分;在每小题给出的选项中,有多项符合题目要求,全部选对的得3分,有选错的得0分,部分选对的得2分)
9.如图,D、E分别是△ABC的边AB、BC上的点,DE∥AC,且D、E分别为BA、BC边上靠近点B的三等分点,则下列结论正确的是
.
A.DE:AC=1:3;
B.OD:OC=1:2;
C.S△BDE:S△CDE=1:2;
D.S△DOE:S△AOC=1:4.
10.函数y=与y=kx2﹣k(k≠0)在同一直角坐标系中的图象可能是( )
A.
B.
C.
D.
11.如图,⊙O是正八边形ABCDEFGH的外接圆,则下列四个结论中正确的是
.
A.的度数为45°;
B.AE=DF;
C.△ODE为等边三角形;
D.S正八边形ABCDEFGH=AE?DF.
12.二次函数y=ax2+bx+c(a,b,c为常数,a≠0)的部分图象如图所示,图象顶点的坐标为(2,1),与x轴的一个交点在点(3,0)和点(4,0)之间,给出的四个结论中正确的有
.
A.b2<4ac;
B.a﹣b+c<0;
C.c﹣4a=1;
D.m≤1时,方程ax2+bx+c=m有解.
三、填空题(本题共6小题,共18分.只要求填写最后结果,每小题填对得3分)
13.已知平行四边形ABCD在平面直角坐标系中的位置如图所示,点D的坐标为(﹣12,9),点A的坐标为(﹣15,0).以B为位似中心,作平行四边形ABCD的位似图形平行四边形EBFG,位似图形与原图形的位似比为2:3,点C的对应点为点F,则点F的坐标为
.(写出一个即可)
14.若x1,x2是一元二次方程x2﹣1011x+1010=0的两个实数根,则x1+x2+x1x2=
.
15.如图,为了测量河宽CD,先在A处测得对岸C点在其北偏东30°方向,然后沿河岸直行100米到点B,在B点测得对岸C点在其北偏西45°方向,则河宽CD是
米.(结果保留根号)
16.正方形ABCD的边长为2,以各边为直径在正方形内画半圆,得到如图所示阴影部分,若随机向正方形ABCD内投一粒米,则米粒落在阴影部分的概率为
.
17.如图,A、B分别是反比例函数y=(x>0)图象上的两点,连接OA,OB,分别过点A、B作x轴的垂线,垂足分别为C、E,且AC交OB于点D,若AD=CD,则的值为
.
18.如图,AB、CD是半径为5的⊙O的两条弦,AB=8,CD=6,MN是直径,AB⊥MN于点E,CD⊥MN于点F,P为EF上的任意一点,则PA+PC的最小值为
.
四、解答题(本题共7小题,共66分.解答应写出文字说明、证明过程或推演步骤)
19.已知二次函数y=x2﹣4x+m(m为常数).
(1)若其图象与x轴有两个交点,求m的取值范围;
(2)求其图象与直线y=m+5交点的横坐标.
20.某市为了解八年级学生数数学学习状况,以2.5%的比例随机抽取了八年级部分学生进行了数学测试(满分100分),测试后将成绩绘制成两幅不完整的统计图表,如下图表所示,测试成绩中没有满分和低于20分的成绩.请根据统计图表中的信息解决下列问题:
八年级数学频数、频率分布表
分数段
频数
频率
90≤x<100
2
0.008
80≤x<90
8
0.032
70≤x<80
a
n
60≤x<70
85
0.340
50≤x<60
b
0.260
40≤x<50
48
0.192
30≤x<40
5
0.020
20≤x<30
2
0.008
(1)直接写出表中a,b的值,并补全频数分布直方图;
(2)若把成绩在80≤x<100范围内的学生视为数学“特长生”,估计该市八年级学生中有多少名数学“特长生”?
(3)在“90≤x<100”和“20≤x<30”分数段的4名同学中,男女各有2名,现从中随机选取两人进行座谈,请用列表或画树状图的方法求出恰好选中一男一女的概率.
21.如图,一次函数y=mx+b与反比例函数y=的图象交于A,B两点,OB=,且点B的横坐标是该点纵坐标的2倍.该一次函数与y轴交于点C,与x轴交于点D.
(1)求点B的坐标及一次函数的解析式;
(2)求△ABO的面积S;
(3)直接写出不等式mx+b≥的解集.
22.如图,矩形EFGH内接于△ABC(矩形各顶点在三角形边上),E,F在BC上,H,G分别在AB,AC上,且AD⊥BC于点D,交HG于点N.
(1)求证:△AHG∽△ABC;
(2)若AD=3,BC=9,设EH=x,矩形EFGH的面积为y,求出y与x之间的函数表达式,并写出自变量x的取值范围.
23.某公司推出一款电子产品,经市场调查发现,该产品的日销售量y(个)与销售单价x(元/个)之间满足一次函数关系.销售单价、日销售量、日销售利润的几组对应值如表:
销售单价x(元/个)
60
65
70
75
日销售量y(个)
180
130
80
30
日销售利润w(元)
1800
1950
1600
750
注:日销售利润=日销售量×(销售单价﹣成本单价)
(1)求y关于x的函数表达式;
(2)该产品的成本价是
元/个,求日销售利润w的最大值;
(3)直接写出单价x满足什么条件时,销售利润不低于1920元.
24.如图,已知Rt△ABC中,∠ACB=90°,AD平分∠BAC,交BC于点D,以AB上某一点O为圆心作⊙O使⊙O经过点A和点D,交AB于点E,连接ED并延长交AC的延长线于点F.
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若AE=12,CF=3,求BE的长;
(3)在(2)的条件下,求阴影区域的面积.
25.如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c经过A(﹣3,0)、B(1,0)两点,与y轴交于点C,连接BC.点P是位于x轴上方抛物线上的一个动点,过P作PE⊥x轴,垂足为点E.
(1)求抛物线的函数表达式;
(2)是否存在点P,使得以A、P、E为顶点的三角形与△BOC相似?若存在,求出点P的坐标;若不存在,说明理由;
(3)是否存在点P,使得四边形ABCP的面积最大?若存在,请求出点P的坐标;若不存在,请说明理由.
参考答案
一、单选题(本题共8小题,共24分.在每个小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来,每小题选对得3分,错选、不选或选出的答案超过一个均记0分)
1.函数y=中,自变量x的取值范围是( )
A.x>1
B.x≥1
C.x<1
D.x≤1
解:由题意得,x﹣1≥0,
解得x≥1.
故选:B.
2.下列说法正确的是( )
A.“概率为0.0001的事件”是不可能事件
B.任意掷一枚质地均匀的硬币10次,正面向上的一定是5次
C.“任意画出一个等边三角形,它是轴对称图形”是随机事件
D.“任意画出一个平行四边形,它是中心对称图形”是必然事件
解:A、“概率为0.0001的事件”是随机事件,选项错误;
B、任意掷一枚质地均匀的硬币10次,正面向上的可能是5次,选项错误;
C、“任意画出一个等边三角形,它是轴对称图形”是必然事件,选项错误;
D、“任意画出一个平行四边形,它是中心对称图形”是必然事件,选项正确;
故选:D.
3.如图,⊙O的半径为3,AB为弦,若∠ABC=30°,则的长为( )
A.π
B.1
C.1.5
D.1.5π
解:
连接OA、OC,
∵∠ABC=30°,
∴∠AOC=2∠ABC=60°,
∵⊙O的半径为3,
∴的长为=π,
故选:A.
4.若关于x的方程(m+1)x2﹣2x﹣1=0有实数根,则m的取值范围是( )
A.m>﹣2
B.m≥﹣2
C.m>﹣2且m≠﹣1
D.m≥﹣2且m≠﹣1
解:当m+1=0时,即m=﹣1时,此时方程为﹣2x﹣1=0,该方程有解,此时m=﹣1;
当m+1≠0时,则方程(m+1)x2﹣2x﹣1=0为一元二次方程,其判别式为Δ=(﹣2)2﹣4(m+1)×(﹣1)=8+4m,
∵方程(m+1)x2﹣2x﹣1=0有实数根,
∴8+4m≥0,解得m≥﹣2;
此时m的取值范围是m≥﹣2且m≠﹣1;
综上可知m的取值范围是m≥﹣2,
故选:B.
5.点P1(﹣0.5,y1),P2(2.5,y2),P3(﹣5,y3)均在二次函数y=﹣x2+2x的图象上,则y1,y2,y3的大小关系是( )
A.y3>y2>y1
B.y3>y1=y2
C.y1>y2>y3
D.y1=y2>y3
解:∵y=﹣x2+2x=﹣(x﹣1)2+1,
∴抛物线对称轴为直线x=1,
∵a=﹣1<0,
∴x<1时,y随x的增大而增大,
∵P2(2.5,y2)的对称点为(﹣0.5,y2),且﹣5<﹣0.5<1,
∴y1=y2>y3.
故选:D.
6.为了响应“绿水青山就是金山银山”的号召,建设生态文明,某工厂自2019年1月开始限产进行治污改造,其月利润y(万元)与月份x之间的变化如图所示,治污完成前是反比例函数图象的一部分,治污完成后是一次函数图象的一部分,下列选项错误的是( )
A.4月份的利润为50万元
B.治污改造完成后每月利润比前一个月增加30万元
C.治污改造完成前后共有4个月的利润低于100万元
D.9月份该厂利润达到200万元
解:A、设反比例函数的解析式为y=,
把(1,200)代入得,k=200,
∴反比例函数的解析式为:y=,
当x=4时,y=50,
∴4月份的利润为50万元,故此选项正确,不合题意;
B、治污改造完成后,从4月到6月,利润从50万到110万,故每月利润比前一个月增加30万元,故此选项正确,不合题意;
C、当y=100时,则100=,
解得:x=2,
则只有3月,4月,5月共3个月的利润低于100万元,故此选项不正确,符合题意.
D、设一次函数解析式为:y=kx+b,
则,
解得:,
故一次函数解析式为:y=30x﹣70,
故y=200时,200=30x﹣70,
解得:x=9,
则治污改造完成后的第5个月,即9月份该厂利润达到200万元,故此选项正确,不合题意.
故选:C.
7.如图,⊙O是等边△ABC的内切圆,分别切AB,BC,AC于点E,F,D,P是上一点,则∠EPF的度数是( )
A.65°
B.60°
C.58°
D.50°
解:如图,连接OE,OF.
∵⊙O是△ABC的内切圆,E,F是切点,
∴OE⊥AB,OF⊥BC,
∴∠OEB=∠OFB=90°,
∵△ABC是等边三角形,
∴∠B=60°,
∴∠EOF=120°,
∴∠EPF=∠EOF=60°,
故选:B.
8.数学兴趣小组在一次用频率估计概率的实验中统计了某一结果出现的频率,绘制了如图所示的频率分布散点图,则符合这一结果的实验可能是( )
A.抛掷一枚硬币,正面向上的概率
B.抛掷一枚骰子,朝上一面的点数为质数的概率
C.从装有3个红球、2个白球袋子中,随机摸出一球为红球的概率
D.两人玩“剪刀、石头、布”游戏中,其中一人获胜的概率
解:A、掷一枚硬币,出现正面朝上的概率为,故此选项不符合题意;
B、抛掷一枚骰子,朝上一面的点数为质数的概率为=,故此选项不符合题意;
C.从装有3个红球、2个白球袋子中,随机摸出一球为红球的概率为=,故此选项符合题意;
D.两人玩“剪刀、石头、布”游戏中,其中一人获胜的概率为=,故此选项不符合题意;
故选:C.
二、多选题(本题共4小题,每小题3分,共12分;在每小题给出的选项中,有多项符合题目要求,全部选对的得3分,有选错的得0分,部分选对的得2分)
9.如图,D、E分别是△ABC的边AB、BC上的点,DE∥AC,且D、E分别为BA、BC边上靠近点B的三等分点,则下列结论正确的是 AC .
A.DE:AC=1:3;
B.OD:OC=1:2;
C.S△BDE:S△CDE=1:2;
D.S△DOE:S△AOC=1:4.
解:∵DE∥AC,
∴△BDE∽△BAC,△ODE∽△OCA,
∴,,
∵D、E分别为BA、BC边上靠近点B的三等分点,
∴DE:AC=1:3,OD:OC=1:3,S△BDE:S△CDE=1:2,
∴S△DOE:S△AOC=1:9.
故答案为:AC.
10.函数y=与y=kx2﹣k(k≠0)在同一直角坐标系中的图象可能是( )
A.
B.
C.
D.
解:分两种情况讨论:
①当k<0时,反比例函数y=,在二、四象限,而二次函数y=kx2﹣k开口向下,故A、B、C、D都不符合题意;
②当k>0时,反比例函数y=,在一、三象限,而二次函数y=kx2﹣k开口向上,与y轴交点在原点下方,故选项D正确,
故选:D.
11.如图,⊙O是正八边形ABCDEFGH的外接圆,则下列四个结论中正确的是 B,D .
A.的度数为45°;
B.AE=DF;
C.△ODE为等边三角形;
D.S正八边形ABCDEFGH=AE?DF.
解:连接OF,
∵∠DOE=∠EOF==45°,
∴∠DOF=90°,
∴弧DF的度数为90°,
∴A错误;
∵∠DOF=90°,OD=OF,
∴2OD2=DF2,
∴OD=DF,
∵AE=2OD,
∴AE=DF,
∴B正确;
∵∠DOE=45°,
∴C错误;
∵S四边形ODEF=DF?OE,
∴S正八边形ABCDEFGH=4S四边形ODEF=2DF?OE,
∵OE=AE,
∴S正八边形ABCDEFGH=AE?DF,
∴D正确;
故答案为:B,D.
12.二次函数y=ax2+bx+c(a,b,c为常数,a≠0)的部分图象如图所示,图象顶点的坐标为(2,1),与x轴的一个交点在点(3,0)和点(4,0)之间,给出的四个结论中正确的有 BCD .
A.b2<4ac;
B.a﹣b+c<0;
C.c﹣4a=1;
D.m≤1时,方程ax2+bx+c=m有解.
解:由图象可知,抛物线开口向下,对称轴在y轴的右侧,与y轴的交点在y轴的负半轴,
∵抛物线与x轴有两个交点,
∴Δ>0,
∴b2﹣4ac>0,即b2>4ac,故A错误;
由图象可知,x=﹣1时,y<0,
∴a﹣b+c<0,故B正确;
∵抛物线的顶点坐标为(2,1),
∴﹣=2,b=﹣4a,
∵4a+2b+c=1,
∴4a﹣8a+c=1,即c﹣4a=1,故C正确;
∵抛物线的开口向下,顶点坐标为(2,1),
∴am2+bm+c≤1(m为任意实数),即m≤1时,方程ax2+bx+c=m有解.故D正确.
故答案为:BCD.
三、填空题(本题共6小题,共18分.只要求填写最后结果,每小题填对得3分)
13.已知平行四边形ABCD在平面直角坐标系中的位置如图所示,点D的坐标为(﹣12,9),点A的坐标为(﹣15,0).以B为位似中心,作平行四边形ABCD的位似图形平行四边形EBFG,位似图形与原图形的位似比为2:3,点C的对应点为点F,则点F的坐标为 (﹣2,﹣6)或(2,6) .(写出一个即可)
解:∵平行四边形ABCD,点D的坐标为(﹣12,9),点A的坐标为(﹣15,0),
∴C(3,9),
∵以B为位似中心,点C的对应点为点F,位似图形与原图形的位似比为2:3,
∴点F的坐标为:(3×,9×)或[3×(﹣),9×(﹣)]即(﹣2,﹣6)或(2,6).
故答案为:(﹣2,﹣6)或(2,6).
14.若x1,x2是一元二次方程x2﹣1011x+1010=0的两个实数根,则x1+x2+x1x2= 2021 .
解:∵若x1,x2是一元二次方程x2﹣1011x+1010=0的两个实数根,
∴x1+x2=1011,x1?x2=1010,
∴x1+x2+x1x2=1011+1010=2021.
故答案是:2021.
15.如图,为了测量河宽CD,先在A处测得对岸C点在其北偏东30°方向,然后沿河岸直行100米到点B,在B点测得对岸C点在其北偏西45°方向,则河宽CD是 (150﹣50) 米.(结果保留根号)
解:设CD=x米,
由题意得:CD⊥AB,∠ACD=30°,∠BCD=45°,
∴∠ADC=∠BDC=90°,
∴AD=CD=x米,BD=CD=x米,
∵AD+BD=AB=100米,
∴x+x=100,
解得:x=150﹣50,
即河宽CD是(150﹣50)米,
故答案为:(150﹣50).
16.正方形ABCD的边长为2,以各边为直径在正方形内画半圆,得到如图所示阴影部分,若随机向正方形ABCD内投一粒米,则米粒落在阴影部分的概率为 .
解:正方形的面积为2×2=4,
阴影部分的面积为:4S半圆﹣S正方形=4××π×12﹣4=2π﹣4,
∴P米粒落在阴影部分的概率==,
故答案为:.
17.如图,A、B分别是反比例函数y=(x>0)图象上的两点,连接OA,OB,分别过点A、B作x轴的垂线,垂足分别为C、E,且AC交OB于点D,若AD=CD,则的值为 .
解:设A(a,),a>0,
∵AD=CD且AD⊥x轴,
∴D(a,),
设直线OD的解析式为:y=kx,将D点代入得:
k=,
∴直线OD的解析式为:y=x,
∵B点为直线OD与反比例函数的交点,
∴联立方程得:,
解得:x=﹣(舍去),x=,
∴BE=,CD=,
∴==,
故答案为:.
18.如图,AB、CD是半径为5的⊙O的两条弦,AB=8,CD=6,MN是直径,AB⊥MN于点E,CD⊥MN于点F,P为EF上的任意一点,则PA+PC的最小值为 .
解:连接OB,OC,作CH垂直AB于H.
根据垂径定理,得到BE=AB=4,CF=CD=3,
∴OE===3,
OF===4,
∴CH=OE+OF=3+4=7,
BH=BE+EH=BE+CF=4+3=7,
在直角△BCH中根据勾股定理得到BC=7,
则PA+PC的最小值为.
故答案为:
四、解答题(本题共7小题,共66分.解答应写出文字说明、证明过程或推演步骤)
19.已知二次函数y=x2﹣4x+m(m为常数).
(1)若其图象与x轴有两个交点,求m的取值范围;
(2)求其图象与直线y=m+5交点的横坐标.
解:(1)根据题意得,Δ=b2﹣4ac=16﹣4m>0,
∴m<4;
(2)根据题意得,x2﹣4x+m=m+5,
解得,x1=5,x2=﹣1,
∴图象与直线y=m+5交点的横坐标为5或﹣1.
20.某市为了解八年级学生数数学学习状况,以2.5%的比例随机抽取了八年级部分学生进行了数学测试(满分100分),测试后将成绩绘制成两幅不完整的统计图表,如下图表所示,测试成绩中没有满分和低于20分的成绩.请根据统计图表中的信息解决下列问题:
八年级数学频数、频率分布表
分数段
频数
频率
90≤x<100
2
0.008
80≤x<90
8
0.032
70≤x<80
a
n
60≤x<70
85
0.340
50≤x<60
b
0.260
40≤x<50
48
0.192
30≤x<40
5
0.020
20≤x<30
2
0.008
(1)直接写出表中a,b的值,并补全频数分布直方图;
(2)若把成绩在80≤x<100范围内的学生视为数学“特长生”,估计该市八年级学生中有多少名数学“特长生”?
(3)在“90≤x<100”和“20≤x<30”分数段的4名同学中,男女各有2名,现从中随机选取两人进行座谈,请用列表或画树状图的方法求出恰好选中一男一女的概率.
解:(1)n=1﹣(0.008+0.032+0.260+0.340+0.192+0.020+0.008)=0.14,
抽取的总人数为:2÷0.008=250(人),
a=250×0.14=35(人),
b=250×0.260=65(人).
补全统计图如下:
(2)250÷2.5%×(0.008+0.032)=400(人),
答:该市八年级学生中有400名数学“特长生”.
(3)用A、B表示两名男生,用C、D表示两名女生,画树状图如图:
共有12种等可能的情况,恰好一男一女的种类有8种
所以恰好选中一男一女的概率是=.
21.如图,一次函数y=mx+b与反比例函数y=的图象交于A,B两点,OB=,且点B的横坐标是该点纵坐标的2倍.该一次函数与y轴交于点C,与x轴交于点D.
(1)求点B的坐标及一次函数的解析式;
(2)求△ABO的面积S;
(3)直接写出不等式mx+b≥的解集.
解:(1)如图,过点B作BH⊥x轴于点H,在△OBH中,设BH=x,OB=2x,
∴x2+(2x)2=5,
∴x=1,
∴点B的坐标为(﹣2,﹣1),
∴把(﹣2,﹣1)代入y=得,m=2,
设一次函数的解析式为:y=2x+b,把(﹣2,﹣1)代入得:b=3,
∴一次函数的解析式为y=2x+3;
(2)由得点A坐标为,
由直线y=2x+3可知,点C坐标为(0,3),OC=3,
∵S△AOB=S△AOC+S△BOC,
∴;
(3)由图象可知,不等式mx+b≥的解集为.
22.如图,矩形EFGH内接于△ABC(矩形各顶点在三角形边上),E,F在BC上,H,G分别在AB,AC上,且AD⊥BC于点D,交HG于点N.
(1)求证:△AHG∽△ABC;
(2)若AD=3,BC=9,设EH=x,矩形EFGH的面积为y,求出y与x之间的函数表达式,并写出自变量x的取值范围.
解:(1)证明:∵四边形EFGH是矩形,
∵HG∥BC,
∴,
∵∠HAG=∠BAC,
∴△AHG∽△ABC,
(2)解:∵四边形EFGH是矩形,
∴∠HED=∠EHN=90°,
∵AD⊥BC,
∴四边形HEDN是矩形,EH=x,
∴ND=EH=x,
∵AD=3,
∴AN=3﹣x,
∵△AHG∽△ABC,
∴,
∴,
∴HG=9﹣3x,
∵矩形EFGH的面积=HG?HE
∴y=x(9﹣3x)=﹣3x2+9x(0<x<3).
23.某公司推出一款电子产品,经市场调查发现,该产品的日销售量y(个)与销售单价x(元/个)之间满足一次函数关系.销售单价、日销售量、日销售利润的几组对应值如表:
销售单价x(元/个)
60
65
70
75
日销售量y(个)
180
130
80
30
日销售利润w(元)
1800
1950
1600
750
注:日销售利润=日销售量×(销售单价﹣成本单价)
(1)求y关于x的函数表达式;
(2)该产品的成本价是 50 元/个,求日销售利润w的最大值;
(3)直接写出单价x满足什么条件时,销售利润不低于1920元.
解:(1)设y关于x的函数表达式为y=kx+b,
把(60,180),(65,130)代入得:
,
解得:,
∴y关于x的函数表达式为y=﹣10x+780;
(2)由表中数据知,当x=60时,y=180,w=1800,
∴该产品的成本价为60﹣1800÷180=50(元/个),
故答案为:50;
根据题意得,w=(x﹣50)(﹣10x+780)
∴w=10x2+1280x﹣39000=﹣10(x﹣64)2+1960
∴当x=64时,w最大为1960元;
(3)由题意得:﹣10(x﹣64)2+1960≥1920,
即﹣10(x﹣64)2≥﹣40,
解得:62≤x≤66,
∴当62≤x≤66时,销售利润不低于1920元.
24.如图,已知Rt△ABC中,∠ACB=90°,AD平分∠BAC,交BC于点D,以AB上某一点O为圆心作⊙O使⊙O经过点A和点D,交AB于点E,连接ED并延长交AC的延长线于点F.
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若AE=12,CF=3,求BE的长;
(3)在(2)的条件下,求阴影区域的面积.
【解答】(1)证明:直线BC与⊙O相切,理由如下:
如图,连接OD,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵OA=OD,
∴∠BAD=∠ODA,
∴∠ODA=∠CAD,
∴OD∥AC,
∵∠ACB=90°,
∵∠ODB=∠ACB=90°,
∴OD⊥BC,
∴BC是⊙O的切线;
(2)解:∵AE是⊙O直径,
∴∠ADE=90°,
∴AD⊥EF,
∵AD平分∠BAC,AE=12,
∴AE=AF=12,
∵CF=3,
∴AC=9,
在Rt△ADF中,∠ACD=90°,
∴∠FDC+∠ADC=∠CAD+∠ADC,
∴∠FDC=∠CAD,
∵∠DCF=∠ACD=90°,
∴△DCF∽△ACD,
∴=,
∴CD2=AC?CF,
∴,
∵tan∠CAD===,
∴∠CAD=30°,
∴∠BAD=30°,
∴∠B=90°﹣∠BAC=30°,
在Rt△ABC中,AC=9,
∴AB=18,
∴BE=18﹣12=6;
(3)解:∵OD⊥BC,∠B=30°,OD=AE=6,
∴,
∴,
∵∠BAD=30°,
∴∠BOD=60°,
∴S扇形EOD==6π,
∴.
25.如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c经过A(﹣3,0)、B(1,0)两点,与y轴交于点C,连接BC.点P是位于x轴上方抛物线上的一个动点,过P作PE⊥x轴,垂足为点E.
(1)求抛物线的函数表达式;
(2)是否存在点P,使得以A、P、E为顶点的三角形与△BOC相似?若存在,求出点P的坐标;若不存在,说明理由;
(3)是否存在点P,使得四边形ABCP的面积最大?若存在,请求出点P的坐标;若不存在,请说明理由.
解:(1)把A(﹣3,0)、B(1,0)代入y=﹣x2+bx+c得:
,
解得:,
∴抛物线的函数解析式为y=﹣x2﹣2x+3;
(2)∵A(﹣3,0),B(1,0),C(0,3),
∴OC=3,OB=1,
∴设P(m,﹣m2﹣2m+3),
∴PE=﹣m2﹣2m+3,AE=m+3,
根据题意得:,
解得:m1=﹣2,m2=﹣3(舍去),
∴P1(﹣2,3),
或,
解得:(舍去),
∴,
综上,点P坐标为P1(﹣2,3)或.
(3)连接AC交PE于点H,
由A(﹣3,0),C(0,3)得直线AC的表达式为:y=x+3,
设P(m,﹣m2﹣2m+3),则H(m,m+3),
∴PH=﹣m2﹣3m
∴
∴S四边形ABCP=S△PAC+S△ABC==
当时,,此时点P的坐标为(﹣,).
同课章节目录
