2020-2021学年安徽省合肥市庐江县九年级(上)期末数学试卷(word解析版)
文档属性
| 名称 | 2020-2021学年安徽省合肥市庐江县九年级(上)期末数学试卷(word解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-22 21:53:31 | ||
图片预览



文档简介
2020-2021学年安徽省合肥市庐江县九年级第一学期期末数学试卷
一、选择题(共10小题,每小题4分,满分40分).
1.下列四个图形分别是四届国际数学家大会的会标,其中不属于中心对称图形的是( )
A.
B.
C.
D.
2.下列说法正确的是( )
A.可能性很大的事情是必然发生的
B.可能性很小的事情是不可能发生的
C.“掷一次骰子,向上一面的点数是6”是不可能事件
D.“任意画出一个平行四边形,它是中心对称图形”是必然事件
3.方程3x(x﹣1)=2(x﹣1)的解是( )
A.x=1
B.x=
C.x1=1,x2=
D.x1=1,x2=﹣
4.将抛物线y=(x+1)2+3向右平移1个单位,再向下平移2个单位后,所得抛物线的解析式为( )
A.y=(x+2)2
B.y=x2+1
C.y=(x+2)2﹣5
D.y=x2+5
5.已知抛物线y=x2﹣x﹣1与x轴的一个交点为(m,0),则代数式m2﹣m+2021的值为( )
A.2020
B.2021
C.2022
D.2023
6.如图,AB是⊙O的直径,PA切⊙O于点A,连接PO并延长交⊙O于点C,连接AC,AB=10,∠P=30°,则AC的长度是( )
A.
B.
C.5
D.
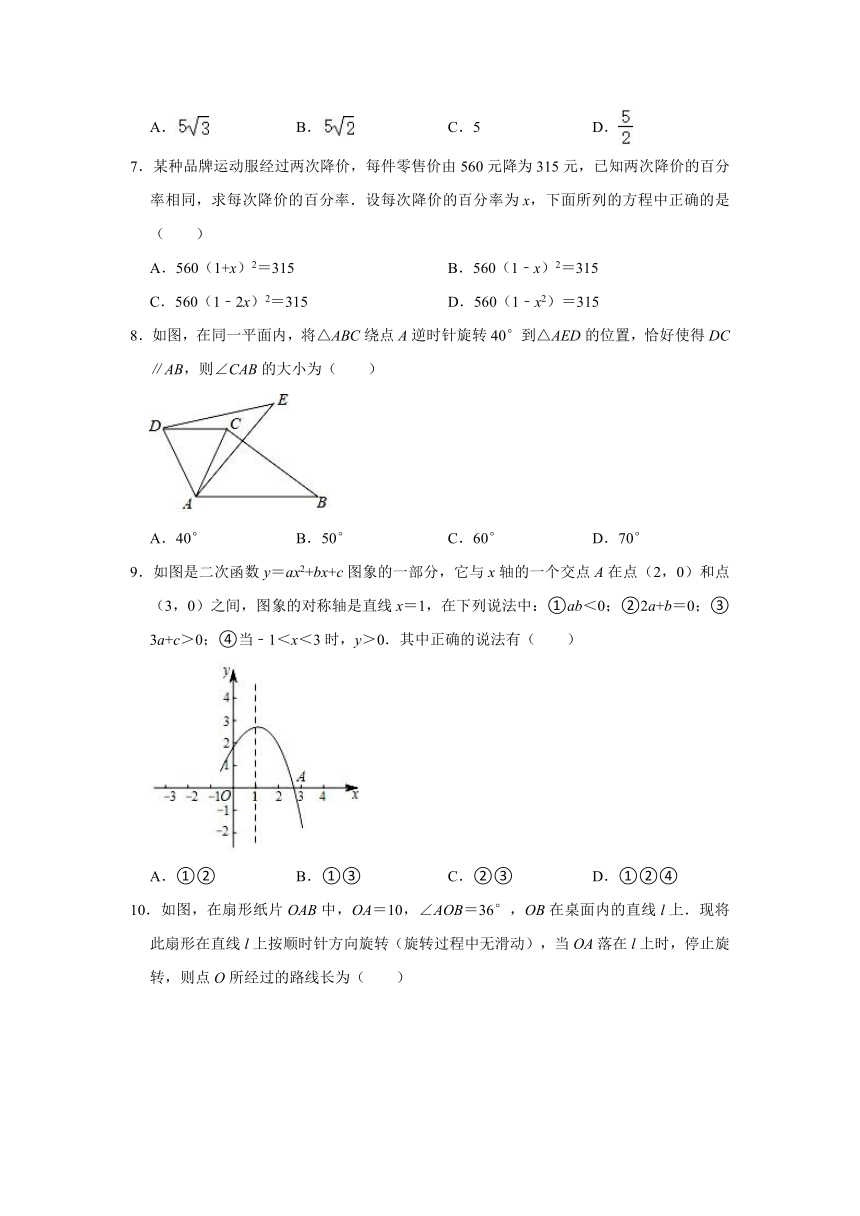
7.某种品牌运动服经过两次降价,每件零售价由560元降为315元,已知两次降价的百分率相同,求每次降价的百分率.设每次降价的百分率为x,下面所列的方程中正确的是( )
A.560(1+x)2=315
B.560(1﹣x)2=315
C.560(1﹣2x)2=315
D.560(1﹣x2)=315
8.如图,在同一平面内,将△ABC绕点A逆时针旋转40°到△AED的位置,恰好使得DC∥AB,则∠CAB的大小为( )
A.40°
B.50°
C.60°
D.70°
9.如图是二次函数y=ax2+bx+c图象的一部分,它与x轴的一个交点A在点(2,0)和点(3,0)之间,图象的对称轴是直线x=1,在下列说法中:①ab<0;②2a+b=0;③3a+c>0;④当﹣1<x<3时,y>0.其中正确的说法有( )
A.①②
B.①③
C.②③
D.①②④
10.如图,在扇形纸片OAB中,OA=10,∠AOB=36°,OB在桌面内的直线l上.现将此扇形在直线l上按顺时针方向旋转(旋转过程中无滑动),当OA落在l上时,停止旋转,则点O所经过的路线长为( )
A.13π
B.12π
C.11π
D.10π
二、填空题(本题共4小题,每小题5分,满分20分)
11.关于x的方程(a﹣5)x2﹣4x﹣1=0有实数根,则a满足
.
12.如图,A、B、C、D均在⊙O上,E为BC延长线上的一点,若∠A=102°,则∠DCE=
.
13.已知抛物线y1=a(x﹣m)2+k与y2=﹣a(x+m)2﹣k(m≠0)关于原点对称,我们称y1与y2互为“和谐抛物线”.请写出抛物线y=﹣4x2+6x+7的“和谐抛物线”
.
14.如图,点A、B、C、D分别在正方形网格的格点上,其中A点的坐标为(﹣1,5),B点的坐标为(3,3),小明发现,线段AB与线段CD存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,则这个旋转中心的坐标是
.
三、(本题共2小题,每小题8分,满分16分)
15.解方程:﹣4x(3x+1)=3(3x+1).
16.如图,在⊙O中,直径AB⊥弦CD于点M,AM=18,BM=8,求CD的长.
四、(本题共2小题,每小题8分,满分16分)
17.已知二次函数y=ax2﹣2x+c的图象经过点A(﹣2,0)、B(3,0).
(1)求二次函数的解析式;
(2)求此抛物线的对称轴和顶点坐标.
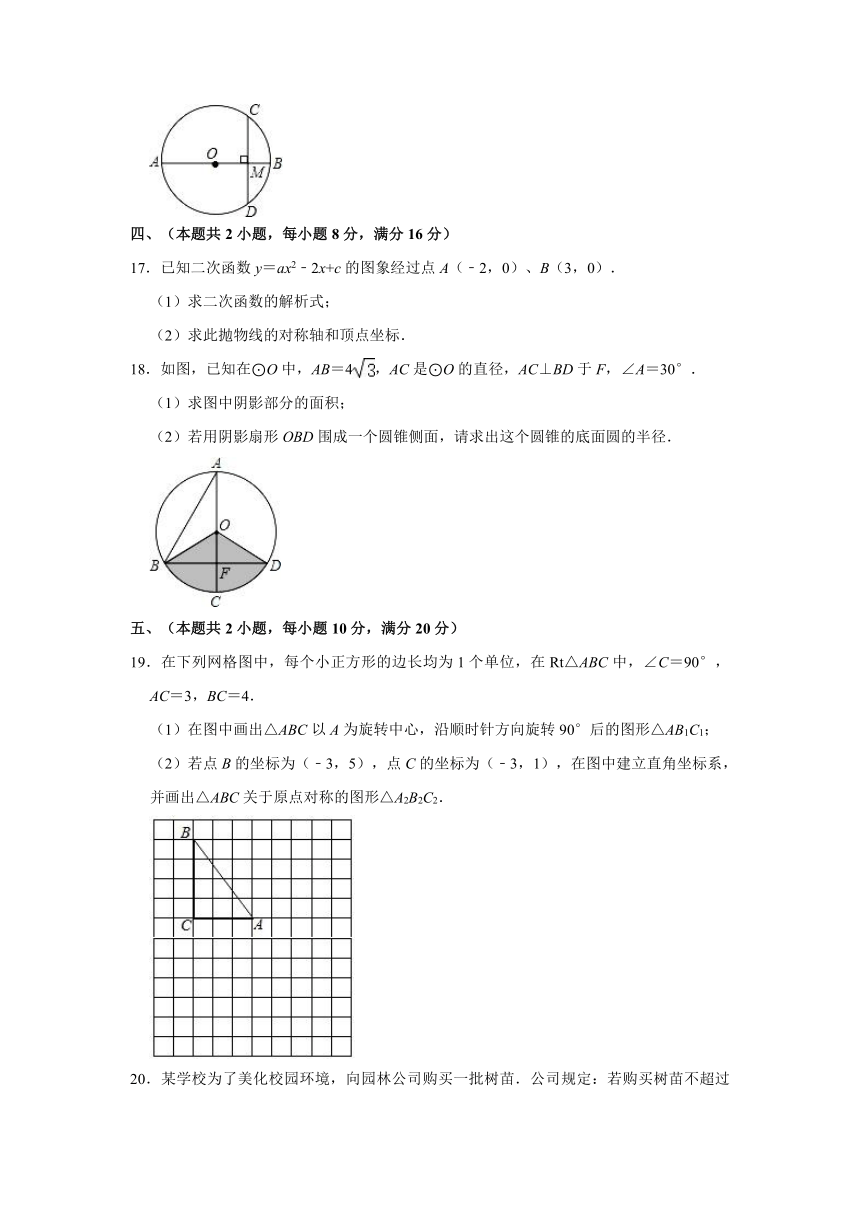
18.如图,已知在⊙O中,AB=4,AC是⊙O的直径,AC⊥BD于F,∠A=30°.
(1)求图中阴影部分的面积;
(2)若用阴影扇形OBD围成一个圆锥侧面,请求出这个圆锥的底面圆的半径.
五、(本题共2小题,每小题10分,满分20分)
19.在下列网格图中,每个小正方形的边长均为1个单位,在Rt△ABC中,∠C=90°,AC=3,BC=4.
(1)在图中画出△ABC以A为旋转中心,沿顺时针方向旋转90°后的图形△AB1C1;
(2)若点B的坐标为(﹣3,5),点C的坐标为(﹣3,1),在图中建立直角坐标系,并画出△ABC关于原点对称的图形△A2B2C2.
20.某学校为了美化校园环境,向园林公司购买一批树苗.公司规定:若购买树苗不超过60棵,则每棵树苗售价120元;若购买树苗超过60棵,则每增加1棵,每棵树苗售价均降低0.5元,且每棵树苗的售价降到100元后,不管购买多少棵树苗,每棵树苗售价均为100元.如果该学校向园林公司支付树苗款8800元,那么这所学校购买了多少棵树苗?
六、(本题满分12分)
21.在一次数学兴趣小组活动中,李燕和刘凯两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形,并在每个扇形区域内标上数字).游戏规则如下:两人分别同时转动甲、乙转盘,转盘停止后,若指针所指区域内两数和小于12,则李燕获胜;若指针所指区域内两数和等于12,则为平局;若指针所指区域内两数和大于12,则刘凯获胜(若指针停在等分线上,重转一次,直到指针指向某一份内为止).
(1)请用列表或画树状图的方法表示出上述游戏中两数和的所有可能的结果;
(2)分别求出李燕和刘凯获胜的概率.
七、(本题满分12分)
22.如图,在平面直角坐标系中,二次函数的图象交坐标轴于A(﹣1,0),B(4,0),C(0,﹣4)三点,点P是直线BC下方抛物线上一动点.
(1)求这个二次函数的解析式;
(2)是否存在点P,使△POC是以OC为底边的等腰三角形?若存在,求出P点坐标;若不存在,请说明理由;
(3)动点P运动到什么位置时,△PBC面积最大,求出此时P点坐标和△PBC的最大面积.
八、(本题满分14分)
23.通过类比联想、引申拓展研究典型题目,可以达到解一题知一类题的目的.下面是一个案例,请补充完整.
原题;如图①,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,试说明理由.
(1)【思路梳理】
∵AB=AD,∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,∵∠ADG=∠B=90°,∴∠FDG=180°,即:点F、D、G共线,根据“SAS”,易证△AFG≌
,得EF=FG=BE+DF;
(2)【类比引申】
如图②,四边形ABCD中,AB=AD,∠BAD=90°,点E、F分别在BC、CD上,∠EAF=45°,若∠B,∠D都不是直角,则当∠B与∠D满足等量关系
时,仍有EF=BE+DF;
(3)【联想拓展】
如图③,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°,猜想BD,DE,EC应满足的等量关系,并写出推理过程.
参考答案
一、选择题(共10小题,每小题4分,满分40分).
1.下列四个图形分别是四届国际数学家大会的会标,其中不属于中心对称图形的是( )
A.
B.
C.
D.
解:A、不是中心对称图形,故此选项正确;
B、是中心对称图形,故此选项错误;
C、是中心对称图形,故此选项错误;
D、是中心对称图形,故此选项错误;
故选:A.
2.下列说法正确的是( )
A.可能性很大的事情是必然发生的
B.可能性很小的事情是不可能发生的
C.“掷一次骰子,向上一面的点数是6”是不可能事件
D.“任意画出一个平行四边形,它是中心对称图形”是必然事件
解:A、可能性很大的事情不一定是必然发生的,本选项说法错误;
B、可能性很小的事情是可能发生的,本选项说法错误;
C、“掷一次骰子,向上一面的点数是6”是随机事件,本选项说法错误;
D、“任意画出一个平行四边形,它是中心对称图形”是必然事件,本选项说法正确;
故选:D.
3.方程3x(x﹣1)=2(x﹣1)的解是( )
A.x=1
B.x=
C.x1=1,x2=
D.x1=1,x2=﹣
解:∵方程3x(x﹣1)=2(x﹣1),
∴(x﹣1)(3x﹣2)=0,
∴x﹣1=0或3x﹣2=0,
∴x1=1,x2=.
故选:C.
4.将抛物线y=(x+1)2+3向右平移1个单位,再向下平移2个单位后,所得抛物线的解析式为( )
A.y=(x+2)2
B.y=x2+1
C.y=(x+2)2﹣5
D.y=x2+5
解:将抛物线y=(x+1)2+3向右平移1个单位,再向下平移2个单位后,所得抛物线的解析式为:y=(x+1﹣1)2+3﹣2,即y=x2+1.
故选:B.
5.已知抛物线y=x2﹣x﹣1与x轴的一个交点为(m,0),则代数式m2﹣m+2021的值为( )
A.2020
B.2021
C.2022
D.2023
解:∵抛物线y=x2﹣x﹣2与x轴的一个交点为(m,0),
∴m2﹣m﹣1=0,
∴m2﹣m=1,
∴m2﹣m+2021=1+2021=2022.
故选:C.
6.如图,AB是⊙O的直径,PA切⊙O于点A,连接PO并延长交⊙O于点C,连接AC,AB=10,∠P=30°,则AC的长度是( )
A.
B.
C.5
D.
解:
方法1、过点O作OD⊥AC于点D,
∵AB是⊙O的直径,PA切⊙O于点A,
∴AB⊥AP,
∴∠BAP=90°,
∵∠P=30°,
∴∠AOP=60°,
∴∠AOC=120°,
∵OA=OC,
∴∠OAD=30°,
∵AB=10,
∴OA=5,
∴OD=AO=2.5,
∴AD==,
∴AC=2AD=5,
故选A,
方法2、如图,
连接BC,∵AP是⊙O的切线,
∴∠BAP=90°,
∵∠P=30°,
∴∠AOP=60°,
∴∠BOC=60°,
∴∠ACP=∠BAC=∠BOC=30°=∠P,
∴AP=AC,
∵AB是⊙O直径,
∴∠ACB=90°,
在Rt△ABC中,∠BAC=30°,AB=10,
∴AC=5,
故选:A.
7.某种品牌运动服经过两次降价,每件零售价由560元降为315元,已知两次降价的百分率相同,求每次降价的百分率.设每次降价的百分率为x,下面所列的方程中正确的是( )
A.560(1+x)2=315
B.560(1﹣x)2=315
C.560(1﹣2x)2=315
D.560(1﹣x2)=315
解:设每次降价的百分率为x,由题意得:
560(1﹣x)2=315,
故选:B.
8.如图,在同一平面内,将△ABC绕点A逆时针旋转40°到△AED的位置,恰好使得DC∥AB,则∠CAB的大小为( )
A.40°
B.50°
C.60°
D.70°
解:∵△ABC绕点A逆时针旋转40°到△AED的位置,
∴AC=AD,∠CAD=40°,
∴∠ACD=∠ADC=70°,
∵DC∥AB,
∴∠CAB=∠ACD=70°,
故选:D.
9.如图是二次函数y=ax2+bx+c图象的一部分,它与x轴的一个交点A在点(2,0)和点(3,0)之间,图象的对称轴是直线x=1,在下列说法中:①ab<0;②2a+b=0;③3a+c>0;④当﹣1<x<3时,y>0.其中正确的说法有( )
A.①②
B.①③
C.②③
D.①②④
解:由图象可知a<0,b>0,c>0,
故ab<0,则①正确;
∵对称轴直线为x==1,
∴b=﹣2a,
∴2a+b=0,则②正确;
由图象可得图象与x轴的另一个交点在(﹣1,0)和(0,0)之间,
则当x=﹣1时,y=a﹣b+c<0,
又a﹣b+c=a﹣(﹣2a)+c=3a+c<0,
则③错误;
观察图象可知,当﹣1<x<3时,y不只是大于0,
则④错误.
综上,只有①②正确.
故选:A.
10.如图,在扇形纸片OAB中,OA=10,∠AOB=36°,OB在桌面内的直线l上.现将此扇形在直线l上按顺时针方向旋转(旋转过程中无滑动),当OA落在l上时,停止旋转,则点O所经过的路线长为( )
A.13π
B.12π
C.11π
D.10π
解:点O经过的路径长为:
l总路线长=
=
=12π.
故选:B.
二、填空题(本题共4小题,每小题5分,满分20分)
11.关于x的方程(a﹣5)x2﹣4x﹣1=0有实数根,则a满足 a≥1 .
解:(1)当a﹣5=0即a=5时,方程变为﹣4x﹣1=0,此时方程一定有实数根;
(2)当a﹣5≠0即a≠5时,
∵关于x的方程(a﹣5)x2﹣4x﹣1=0有实数根
∴16+4(a﹣5)≥0,
∴a≥1.
所以a的取值范围为a≥1.
故答案为:a≥1.
12.如图,A、B、C、D均在⊙O上,E为BC延长线上的一点,若∠A=102°,则∠DCE= 102° .
解:连接OB,OD,
∵∠DOB与∠A都对,∠DOB(大于平角的角)与∠BCD都对,
∴∠DOB=2∠A,∠DOB(大于平角的角)=2∠BCD,
∵∠DOB+∠DOB(大于平角的角)=360°,
∴∠A+∠BCD=180°,
∵∠DCE+∠BCD=180°,
∴∠DCE=∠A=102°,
故答案为:102°
13.已知抛物线y1=a(x﹣m)2+k与y2=﹣a(x+m)2﹣k(m≠0)关于原点对称,我们称y1与y2互为“和谐抛物线”.请写出抛物线y=﹣4x2+6x+7的“和谐抛物线” y=4x2+6x﹣7 .
解:抛物线y=﹣4x2+6x+7的“和谐抛物线”是y=﹣4(﹣x)2﹣6(﹣x)﹣7,
化简,得y=4x2+6x﹣7,
故答案为:y=4x2+6x﹣7.
14.如图,点A、B、C、D分别在正方形网格的格点上,其中A点的坐标为(﹣1,5),B点的坐标为(3,3),小明发现,线段AB与线段CD存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,则这个旋转中心的坐标是 (1,1)或(4,4). .
解:如图所示,分两种情形,旋转中心分别为(1,1)或(4,4);
故答案为(1,1)或(4,4).
三、(本题共2小题,每小题8分,满分16分)
15.解方程:﹣4x(3x+1)=3(3x+1).
解:∵﹣4x(3x+1)=3(3x+1),
∴3(3x+1)+4x(3x+1)=0,
则(3x+1)(3+4x)=0,
∴3x+1=0或3+4x=0,
解得,.
16.如图,在⊙O中,直径AB⊥弦CD于点M,AM=18,BM=8,求CD的长.
解:连接OC,
∵AM=18,BM=8,
∴半径OC=OA=OB=13,
∴OM=5,
∵直径AB⊥弦CD于点M,
∴CD=2CM=2DM,
在Rt△OCM中,由勾股定理得:CM==12,
∴CD=24.
四、(本题共2小题,每小题8分,满分16分)
17.已知二次函数y=ax2﹣2x+c的图象经过点A(﹣2,0)、B(3,0).
(1)求二次函数的解析式;
(2)求此抛物线的对称轴和顶点坐标.
解:(1)∵二次函数y=ax2﹣2x+c的图象经过点A(﹣2,0)、B(3,0).
∴,
∴,
∴二次函数的解析式为:y=2x2﹣2x﹣12;
(2)∵,
∴抛物线的对称轴为直线,顶点坐标为.
18.如图,已知在⊙O中,AB=4,AC是⊙O的直径,AC⊥BD于F,∠A=30°.
(1)求图中阴影部分的面积;
(2)若用阴影扇形OBD围成一个圆锥侧面,请求出这个圆锥的底面圆的半径.
解:(1)法一:过O作OE⊥AB于E,则
BF=AB=2.
在Rt△AEO中,∠BAC=30°,cos30°=.
∴OA===4.
又∵OA=OB,
∴∠ABO=30度.
∴∠BOC=60度.
∵AC⊥BD,∴.
∴∠COD=∠BOC=60度.
∴∠BOD=120度.
∴S阴影==.
法二:连接AD.
∵AC⊥BD,AC是直径,
∴AC垂直平分BD.
∴AB=AD,BF=FD,.
∴∠BAD=2∠BAC=60°,
∴∠BOD=120度.
∵BF=AB=2,sin60°=,
AF=AB?sin60°=4×=6.
∴OB2=BF2+OF2.即.
∴OB=4.
∴S阴影=S圆=.
法三:连接BC.
∵AC为⊙O的直径,
∴∠ABC=90度.
∵AB=4,
∴.
∵∠A=30°,AC⊥BD,
∴∠BOC=60°,∴∠BOD=120度.
∴S阴影=π?OA2=×42?π=.
以下同法一;
(2)设圆锥的底面圆的半径为r,则周长为2πr,
∴.
∴.
五、(本题共2小题,每小题10分,满分20分)
19.在下列网格图中,每个小正方形的边长均为1个单位,在Rt△ABC中,∠C=90°,AC=3,BC=4.
(1)在图中画出△ABC以A为旋转中心,沿顺时针方向旋转90°后的图形△AB1C1;
(2)若点B的坐标为(﹣3,5),点C的坐标为(﹣3,1),在图中建立直角坐标系,并画出△ABC关于原点对称的图形△A2B2C2.
解:如图,
(1)△AB1C1即为所求;
(2)直角坐标系及△A2B2C2即为所求.
20.某学校为了美化校园环境,向园林公司购买一批树苗.公司规定:若购买树苗不超过60棵,则每棵树苗售价120元;若购买树苗超过60棵,则每增加1棵,每棵树苗售价均降低0.5元,且每棵树苗的售价降到100元后,不管购买多少棵树苗,每棵树苗售价均为100元.如果该学校向园林公司支付树苗款8800元,那么这所学校购买了多少棵树苗?
解:∵60×120=7200(元),(120﹣100)÷0.5+60=100(棵),100×100=10000(元),7200<8800<10000,
∴购买的树苗棵树超过60棵,且不足100棵.
设这所学校购买了x棵树苗(60<x<100),则每棵树苗的售价为120﹣0.5(x﹣60)=(150﹣0.5x)元,
依题意得:x(150﹣0.5x)=8800,
整理得:x2﹣300x+17600=0,
解得:x1=80,x2=220(不合题意,舍去).
答:这所学校购买了80棵树苗.
六、(本题满分12分)
21.在一次数学兴趣小组活动中,李燕和刘凯两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形,并在每个扇形区域内标上数字).游戏规则如下:两人分别同时转动甲、乙转盘,转盘停止后,若指针所指区域内两数和小于12,则李燕获胜;若指针所指区域内两数和等于12,则为平局;若指针所指区域内两数和大于12,则刘凯获胜(若指针停在等分线上,重转一次,直到指针指向某一份内为止).
(1)请用列表或画树状图的方法表示出上述游戏中两数和的所有可能的结果;
(2)分别求出李燕和刘凯获胜的概率.
解:(1)根据题意列表如下:
可见,两数和共有12种等可能结果;
(2)由(1)可知,两数和共有12种等可能的情况,其中和小于12的情况有6种,和大于12的情况有3种,
∴李燕获胜的概率为=;
刘凯获胜的概率为=.
七、(本题满分12分)
22.如图,在平面直角坐标系中,二次函数的图象交坐标轴于A(﹣1,0),B(4,0),C(0,﹣4)三点,点P是直线BC下方抛物线上一动点.
(1)求这个二次函数的解析式;
(2)是否存在点P,使△POC是以OC为底边的等腰三角形?若存在,求出P点坐标;若不存在,请说明理由;
(3)动点P运动到什么位置时,△PBC面积最大,求出此时P点坐标和△PBC的最大面积.
解:
(1)设抛物线解析式为y=ax2+bx+c,
把A、B、C三点坐标代入可得,解得,
∴抛物线解析式为y=x2﹣3x﹣4;
(2)作OC的垂直平分线DP,交OC于点D,交BC下方抛物线于点P,如图1,
∴PO=PC,此时P点即为满足条件的点,
∵C(0,﹣4),
∴D(0,﹣2),
∴P点纵坐标为﹣2,
代入抛物线解析式可得x2﹣3x﹣4=﹣2,解得x=(小于0,舍去)或x=,
∴存在满足条件的P点,其坐标为(,﹣2);
(3)∵点P在抛物线上,
∴可设P(t,t2﹣3t﹣4),
过P作PE⊥x轴于点E,交直线BC于点F,如图2,
∵B(4,0),C(0,﹣4),
∴直线BC解析式为y=x﹣4,
∴F(t,t﹣4),
∴PF=(t﹣4)﹣(t2﹣3t﹣4)=﹣t2+4t,
∴S△PBC=S△PFC+S△PFB=PF?OE+PF?BE=PF?(OE+BE)=PF?OB=(﹣t2+4t)×4=﹣2(t﹣2)2+8,
∴当t=2时,S△PBC最大值为8,此时t2﹣3t﹣4=﹣6,
∴当P点坐标为(2,﹣6)时,△PBC的最大面积为8.
八、(本题满分14分)
23.通过类比联想、引申拓展研究典型题目,可以达到解一题知一类题的目的.下面是一个案例,请补充完整.
原题;如图①,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,试说明理由.
(1)【思路梳理】
∵AB=AD,∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,∵∠ADG=∠B=90°,∴∠FDG=180°,即:点F、D、G共线,根据“SAS”,易证△AFG≌ △AFE ,得EF=FG=BE+DF;
(2)【类比引申】
如图②,四边形ABCD中,AB=AD,∠BAD=90°,点E、F分别在BC、CD上,∠EAF=45°,若∠B,∠D都不是直角,则当∠B与∠D满足等量关系 ∠B+∠D=180° 时,仍有EF=BE+DF;
(3)【联想拓展】
如图③,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°,猜想BD,DE,EC应满足的等量关系,并写出推理过程.
解:(1)如图1,∵四边形ABCD是正方形,
∴AB=AD,∠B=∠BAD=∠ADC=90°,
把△ABE绕点A逆时针旋转90°到△ADG,则∠DAG=∠BAE,AG=AE,
∵∠ADG=∠B=90°,
∴∠ADC+∠ADG=180°,
∴点F、D、G在同一条直线上;
∵∠EAF=45°,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=90°﹣45°=45°,
∴∠GAF=∠EAF,
∵AF=AF,
∴△AFG≌△AFE(SAS),
∴EF=GF=DG+DF=BE+DF,
故答案为:△AFE.
(2)如图2,由题意得,AB=AD,∠BAD=90°,
把△ABE绕点A逆时针旋转90°到△ADG,则∠DAG=∠BAE,∠ADG=∠B,AG=AE,
当∠B+∠ADC=180°,即∠B+∠D=180°时,则∠ADG+∠ADC=180°,
∴点F、D、G在同一条直线上;
∵∠EAF=45°,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=90°﹣45°=45°,
∴∠GAF=∠EAF,
∵AF=AF,
∴△AFG≌△AFE(SAS),
∴EF=GF=DG+DF=BE+DF,
故答案为:∠B+∠D=180°.
(3)DE2=BD2+EC2,
证明:如图3,由题意得,AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°;
把△ABD绕点A逆时针旋转90°到△ACG,则∠CAG=∠BAD,∠ACG=∠B=45°,AG=AD,CG=BD,
∴∠ECG=∠ACB+∠ACG=90°;
∵∠DAE=45°,
∵∠GAE=∠CAG+∠CAE=∠BAD+∠CAE=90°﹣45°=45°,
∴∠GAE=∠DAE,
∵AE=AE,
∴△AEG≌△AED(SAS),
∴GE=DE,
∵GE2=CG2+EC2,
∴DE2=BD2+EC2.
一、选择题(共10小题,每小题4分,满分40分).
1.下列四个图形分别是四届国际数学家大会的会标,其中不属于中心对称图形的是( )
A.
B.
C.
D.
2.下列说法正确的是( )
A.可能性很大的事情是必然发生的
B.可能性很小的事情是不可能发生的
C.“掷一次骰子,向上一面的点数是6”是不可能事件
D.“任意画出一个平行四边形,它是中心对称图形”是必然事件
3.方程3x(x﹣1)=2(x﹣1)的解是( )
A.x=1
B.x=
C.x1=1,x2=
D.x1=1,x2=﹣
4.将抛物线y=(x+1)2+3向右平移1个单位,再向下平移2个单位后,所得抛物线的解析式为( )
A.y=(x+2)2
B.y=x2+1
C.y=(x+2)2﹣5
D.y=x2+5
5.已知抛物线y=x2﹣x﹣1与x轴的一个交点为(m,0),则代数式m2﹣m+2021的值为( )
A.2020
B.2021
C.2022
D.2023
6.如图,AB是⊙O的直径,PA切⊙O于点A,连接PO并延长交⊙O于点C,连接AC,AB=10,∠P=30°,则AC的长度是( )
A.
B.
C.5
D.
7.某种品牌运动服经过两次降价,每件零售价由560元降为315元,已知两次降价的百分率相同,求每次降价的百分率.设每次降价的百分率为x,下面所列的方程中正确的是( )
A.560(1+x)2=315
B.560(1﹣x)2=315
C.560(1﹣2x)2=315
D.560(1﹣x2)=315
8.如图,在同一平面内,将△ABC绕点A逆时针旋转40°到△AED的位置,恰好使得DC∥AB,则∠CAB的大小为( )
A.40°
B.50°
C.60°
D.70°
9.如图是二次函数y=ax2+bx+c图象的一部分,它与x轴的一个交点A在点(2,0)和点(3,0)之间,图象的对称轴是直线x=1,在下列说法中:①ab<0;②2a+b=0;③3a+c>0;④当﹣1<x<3时,y>0.其中正确的说法有( )
A.①②
B.①③
C.②③
D.①②④
10.如图,在扇形纸片OAB中,OA=10,∠AOB=36°,OB在桌面内的直线l上.现将此扇形在直线l上按顺时针方向旋转(旋转过程中无滑动),当OA落在l上时,停止旋转,则点O所经过的路线长为( )
A.13π
B.12π
C.11π
D.10π
二、填空题(本题共4小题,每小题5分,满分20分)
11.关于x的方程(a﹣5)x2﹣4x﹣1=0有实数根,则a满足
.
12.如图,A、B、C、D均在⊙O上,E为BC延长线上的一点,若∠A=102°,则∠DCE=
.
13.已知抛物线y1=a(x﹣m)2+k与y2=﹣a(x+m)2﹣k(m≠0)关于原点对称,我们称y1与y2互为“和谐抛物线”.请写出抛物线y=﹣4x2+6x+7的“和谐抛物线”
.
14.如图,点A、B、C、D分别在正方形网格的格点上,其中A点的坐标为(﹣1,5),B点的坐标为(3,3),小明发现,线段AB与线段CD存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,则这个旋转中心的坐标是
.
三、(本题共2小题,每小题8分,满分16分)
15.解方程:﹣4x(3x+1)=3(3x+1).
16.如图,在⊙O中,直径AB⊥弦CD于点M,AM=18,BM=8,求CD的长.
四、(本题共2小题,每小题8分,满分16分)
17.已知二次函数y=ax2﹣2x+c的图象经过点A(﹣2,0)、B(3,0).
(1)求二次函数的解析式;
(2)求此抛物线的对称轴和顶点坐标.
18.如图,已知在⊙O中,AB=4,AC是⊙O的直径,AC⊥BD于F,∠A=30°.
(1)求图中阴影部分的面积;
(2)若用阴影扇形OBD围成一个圆锥侧面,请求出这个圆锥的底面圆的半径.
五、(本题共2小题,每小题10分,满分20分)
19.在下列网格图中,每个小正方形的边长均为1个单位,在Rt△ABC中,∠C=90°,AC=3,BC=4.
(1)在图中画出△ABC以A为旋转中心,沿顺时针方向旋转90°后的图形△AB1C1;
(2)若点B的坐标为(﹣3,5),点C的坐标为(﹣3,1),在图中建立直角坐标系,并画出△ABC关于原点对称的图形△A2B2C2.
20.某学校为了美化校园环境,向园林公司购买一批树苗.公司规定:若购买树苗不超过60棵,则每棵树苗售价120元;若购买树苗超过60棵,则每增加1棵,每棵树苗售价均降低0.5元,且每棵树苗的售价降到100元后,不管购买多少棵树苗,每棵树苗售价均为100元.如果该学校向园林公司支付树苗款8800元,那么这所学校购买了多少棵树苗?
六、(本题满分12分)
21.在一次数学兴趣小组活动中,李燕和刘凯两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形,并在每个扇形区域内标上数字).游戏规则如下:两人分别同时转动甲、乙转盘,转盘停止后,若指针所指区域内两数和小于12,则李燕获胜;若指针所指区域内两数和等于12,则为平局;若指针所指区域内两数和大于12,则刘凯获胜(若指针停在等分线上,重转一次,直到指针指向某一份内为止).
(1)请用列表或画树状图的方法表示出上述游戏中两数和的所有可能的结果;
(2)分别求出李燕和刘凯获胜的概率.
七、(本题满分12分)
22.如图,在平面直角坐标系中,二次函数的图象交坐标轴于A(﹣1,0),B(4,0),C(0,﹣4)三点,点P是直线BC下方抛物线上一动点.
(1)求这个二次函数的解析式;
(2)是否存在点P,使△POC是以OC为底边的等腰三角形?若存在,求出P点坐标;若不存在,请说明理由;
(3)动点P运动到什么位置时,△PBC面积最大,求出此时P点坐标和△PBC的最大面积.
八、(本题满分14分)
23.通过类比联想、引申拓展研究典型题目,可以达到解一题知一类题的目的.下面是一个案例,请补充完整.
原题;如图①,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,试说明理由.
(1)【思路梳理】
∵AB=AD,∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,∵∠ADG=∠B=90°,∴∠FDG=180°,即:点F、D、G共线,根据“SAS”,易证△AFG≌
,得EF=FG=BE+DF;
(2)【类比引申】
如图②,四边形ABCD中,AB=AD,∠BAD=90°,点E、F分别在BC、CD上,∠EAF=45°,若∠B,∠D都不是直角,则当∠B与∠D满足等量关系
时,仍有EF=BE+DF;
(3)【联想拓展】
如图③,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°,猜想BD,DE,EC应满足的等量关系,并写出推理过程.
参考答案
一、选择题(共10小题,每小题4分,满分40分).
1.下列四个图形分别是四届国际数学家大会的会标,其中不属于中心对称图形的是( )
A.
B.
C.
D.
解:A、不是中心对称图形,故此选项正确;
B、是中心对称图形,故此选项错误;
C、是中心对称图形,故此选项错误;
D、是中心对称图形,故此选项错误;
故选:A.
2.下列说法正确的是( )
A.可能性很大的事情是必然发生的
B.可能性很小的事情是不可能发生的
C.“掷一次骰子,向上一面的点数是6”是不可能事件
D.“任意画出一个平行四边形,它是中心对称图形”是必然事件
解:A、可能性很大的事情不一定是必然发生的,本选项说法错误;
B、可能性很小的事情是可能发生的,本选项说法错误;
C、“掷一次骰子,向上一面的点数是6”是随机事件,本选项说法错误;
D、“任意画出一个平行四边形,它是中心对称图形”是必然事件,本选项说法正确;
故选:D.
3.方程3x(x﹣1)=2(x﹣1)的解是( )
A.x=1
B.x=
C.x1=1,x2=
D.x1=1,x2=﹣
解:∵方程3x(x﹣1)=2(x﹣1),
∴(x﹣1)(3x﹣2)=0,
∴x﹣1=0或3x﹣2=0,
∴x1=1,x2=.
故选:C.
4.将抛物线y=(x+1)2+3向右平移1个单位,再向下平移2个单位后,所得抛物线的解析式为( )
A.y=(x+2)2
B.y=x2+1
C.y=(x+2)2﹣5
D.y=x2+5
解:将抛物线y=(x+1)2+3向右平移1个单位,再向下平移2个单位后,所得抛物线的解析式为:y=(x+1﹣1)2+3﹣2,即y=x2+1.
故选:B.
5.已知抛物线y=x2﹣x﹣1与x轴的一个交点为(m,0),则代数式m2﹣m+2021的值为( )
A.2020
B.2021
C.2022
D.2023
解:∵抛物线y=x2﹣x﹣2与x轴的一个交点为(m,0),
∴m2﹣m﹣1=0,
∴m2﹣m=1,
∴m2﹣m+2021=1+2021=2022.
故选:C.
6.如图,AB是⊙O的直径,PA切⊙O于点A,连接PO并延长交⊙O于点C,连接AC,AB=10,∠P=30°,则AC的长度是( )
A.
B.
C.5
D.
解:
方法1、过点O作OD⊥AC于点D,
∵AB是⊙O的直径,PA切⊙O于点A,
∴AB⊥AP,
∴∠BAP=90°,
∵∠P=30°,
∴∠AOP=60°,
∴∠AOC=120°,
∵OA=OC,
∴∠OAD=30°,
∵AB=10,
∴OA=5,
∴OD=AO=2.5,
∴AD==,
∴AC=2AD=5,
故选A,
方法2、如图,
连接BC,∵AP是⊙O的切线,
∴∠BAP=90°,
∵∠P=30°,
∴∠AOP=60°,
∴∠BOC=60°,
∴∠ACP=∠BAC=∠BOC=30°=∠P,
∴AP=AC,
∵AB是⊙O直径,
∴∠ACB=90°,
在Rt△ABC中,∠BAC=30°,AB=10,
∴AC=5,
故选:A.
7.某种品牌运动服经过两次降价,每件零售价由560元降为315元,已知两次降价的百分率相同,求每次降价的百分率.设每次降价的百分率为x,下面所列的方程中正确的是( )
A.560(1+x)2=315
B.560(1﹣x)2=315
C.560(1﹣2x)2=315
D.560(1﹣x2)=315
解:设每次降价的百分率为x,由题意得:
560(1﹣x)2=315,
故选:B.
8.如图,在同一平面内,将△ABC绕点A逆时针旋转40°到△AED的位置,恰好使得DC∥AB,则∠CAB的大小为( )
A.40°
B.50°
C.60°
D.70°
解:∵△ABC绕点A逆时针旋转40°到△AED的位置,
∴AC=AD,∠CAD=40°,
∴∠ACD=∠ADC=70°,
∵DC∥AB,
∴∠CAB=∠ACD=70°,
故选:D.
9.如图是二次函数y=ax2+bx+c图象的一部分,它与x轴的一个交点A在点(2,0)和点(3,0)之间,图象的对称轴是直线x=1,在下列说法中:①ab<0;②2a+b=0;③3a+c>0;④当﹣1<x<3时,y>0.其中正确的说法有( )
A.①②
B.①③
C.②③
D.①②④
解:由图象可知a<0,b>0,c>0,
故ab<0,则①正确;
∵对称轴直线为x==1,
∴b=﹣2a,
∴2a+b=0,则②正确;
由图象可得图象与x轴的另一个交点在(﹣1,0)和(0,0)之间,
则当x=﹣1时,y=a﹣b+c<0,
又a﹣b+c=a﹣(﹣2a)+c=3a+c<0,
则③错误;
观察图象可知,当﹣1<x<3时,y不只是大于0,
则④错误.
综上,只有①②正确.
故选:A.
10.如图,在扇形纸片OAB中,OA=10,∠AOB=36°,OB在桌面内的直线l上.现将此扇形在直线l上按顺时针方向旋转(旋转过程中无滑动),当OA落在l上时,停止旋转,则点O所经过的路线长为( )
A.13π
B.12π
C.11π
D.10π
解:点O经过的路径长为:
l总路线长=
=
=12π.
故选:B.
二、填空题(本题共4小题,每小题5分,满分20分)
11.关于x的方程(a﹣5)x2﹣4x﹣1=0有实数根,则a满足 a≥1 .
解:(1)当a﹣5=0即a=5时,方程变为﹣4x﹣1=0,此时方程一定有实数根;
(2)当a﹣5≠0即a≠5时,
∵关于x的方程(a﹣5)x2﹣4x﹣1=0有实数根
∴16+4(a﹣5)≥0,
∴a≥1.
所以a的取值范围为a≥1.
故答案为:a≥1.
12.如图,A、B、C、D均在⊙O上,E为BC延长线上的一点,若∠A=102°,则∠DCE= 102° .
解:连接OB,OD,
∵∠DOB与∠A都对,∠DOB(大于平角的角)与∠BCD都对,
∴∠DOB=2∠A,∠DOB(大于平角的角)=2∠BCD,
∵∠DOB+∠DOB(大于平角的角)=360°,
∴∠A+∠BCD=180°,
∵∠DCE+∠BCD=180°,
∴∠DCE=∠A=102°,
故答案为:102°
13.已知抛物线y1=a(x﹣m)2+k与y2=﹣a(x+m)2﹣k(m≠0)关于原点对称,我们称y1与y2互为“和谐抛物线”.请写出抛物线y=﹣4x2+6x+7的“和谐抛物线” y=4x2+6x﹣7 .
解:抛物线y=﹣4x2+6x+7的“和谐抛物线”是y=﹣4(﹣x)2﹣6(﹣x)﹣7,
化简,得y=4x2+6x﹣7,
故答案为:y=4x2+6x﹣7.
14.如图,点A、B、C、D分别在正方形网格的格点上,其中A点的坐标为(﹣1,5),B点的坐标为(3,3),小明发现,线段AB与线段CD存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,则这个旋转中心的坐标是 (1,1)或(4,4). .
解:如图所示,分两种情形,旋转中心分别为(1,1)或(4,4);
故答案为(1,1)或(4,4).
三、(本题共2小题,每小题8分,满分16分)
15.解方程:﹣4x(3x+1)=3(3x+1).
解:∵﹣4x(3x+1)=3(3x+1),
∴3(3x+1)+4x(3x+1)=0,
则(3x+1)(3+4x)=0,
∴3x+1=0或3+4x=0,
解得,.
16.如图,在⊙O中,直径AB⊥弦CD于点M,AM=18,BM=8,求CD的长.
解:连接OC,
∵AM=18,BM=8,
∴半径OC=OA=OB=13,
∴OM=5,
∵直径AB⊥弦CD于点M,
∴CD=2CM=2DM,
在Rt△OCM中,由勾股定理得:CM==12,
∴CD=24.
四、(本题共2小题,每小题8分,满分16分)
17.已知二次函数y=ax2﹣2x+c的图象经过点A(﹣2,0)、B(3,0).
(1)求二次函数的解析式;
(2)求此抛物线的对称轴和顶点坐标.
解:(1)∵二次函数y=ax2﹣2x+c的图象经过点A(﹣2,0)、B(3,0).
∴,
∴,
∴二次函数的解析式为:y=2x2﹣2x﹣12;
(2)∵,
∴抛物线的对称轴为直线,顶点坐标为.
18.如图,已知在⊙O中,AB=4,AC是⊙O的直径,AC⊥BD于F,∠A=30°.
(1)求图中阴影部分的面积;
(2)若用阴影扇形OBD围成一个圆锥侧面,请求出这个圆锥的底面圆的半径.
解:(1)法一:过O作OE⊥AB于E,则
BF=AB=2.
在Rt△AEO中,∠BAC=30°,cos30°=.
∴OA===4.
又∵OA=OB,
∴∠ABO=30度.
∴∠BOC=60度.
∵AC⊥BD,∴.
∴∠COD=∠BOC=60度.
∴∠BOD=120度.
∴S阴影==.
法二:连接AD.
∵AC⊥BD,AC是直径,
∴AC垂直平分BD.
∴AB=AD,BF=FD,.
∴∠BAD=2∠BAC=60°,
∴∠BOD=120度.
∵BF=AB=2,sin60°=,
AF=AB?sin60°=4×=6.
∴OB2=BF2+OF2.即.
∴OB=4.
∴S阴影=S圆=.
法三:连接BC.
∵AC为⊙O的直径,
∴∠ABC=90度.
∵AB=4,
∴.
∵∠A=30°,AC⊥BD,
∴∠BOC=60°,∴∠BOD=120度.
∴S阴影=π?OA2=×42?π=.
以下同法一;
(2)设圆锥的底面圆的半径为r,则周长为2πr,
∴.
∴.
五、(本题共2小题,每小题10分,满分20分)
19.在下列网格图中,每个小正方形的边长均为1个单位,在Rt△ABC中,∠C=90°,AC=3,BC=4.
(1)在图中画出△ABC以A为旋转中心,沿顺时针方向旋转90°后的图形△AB1C1;
(2)若点B的坐标为(﹣3,5),点C的坐标为(﹣3,1),在图中建立直角坐标系,并画出△ABC关于原点对称的图形△A2B2C2.
解:如图,
(1)△AB1C1即为所求;
(2)直角坐标系及△A2B2C2即为所求.
20.某学校为了美化校园环境,向园林公司购买一批树苗.公司规定:若购买树苗不超过60棵,则每棵树苗售价120元;若购买树苗超过60棵,则每增加1棵,每棵树苗售价均降低0.5元,且每棵树苗的售价降到100元后,不管购买多少棵树苗,每棵树苗售价均为100元.如果该学校向园林公司支付树苗款8800元,那么这所学校购买了多少棵树苗?
解:∵60×120=7200(元),(120﹣100)÷0.5+60=100(棵),100×100=10000(元),7200<8800<10000,
∴购买的树苗棵树超过60棵,且不足100棵.
设这所学校购买了x棵树苗(60<x<100),则每棵树苗的售价为120﹣0.5(x﹣60)=(150﹣0.5x)元,
依题意得:x(150﹣0.5x)=8800,
整理得:x2﹣300x+17600=0,
解得:x1=80,x2=220(不合题意,舍去).
答:这所学校购买了80棵树苗.
六、(本题满分12分)
21.在一次数学兴趣小组活动中,李燕和刘凯两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形,并在每个扇形区域内标上数字).游戏规则如下:两人分别同时转动甲、乙转盘,转盘停止后,若指针所指区域内两数和小于12,则李燕获胜;若指针所指区域内两数和等于12,则为平局;若指针所指区域内两数和大于12,则刘凯获胜(若指针停在等分线上,重转一次,直到指针指向某一份内为止).
(1)请用列表或画树状图的方法表示出上述游戏中两数和的所有可能的结果;
(2)分别求出李燕和刘凯获胜的概率.
解:(1)根据题意列表如下:
可见,两数和共有12种等可能结果;
(2)由(1)可知,两数和共有12种等可能的情况,其中和小于12的情况有6种,和大于12的情况有3种,
∴李燕获胜的概率为=;
刘凯获胜的概率为=.
七、(本题满分12分)
22.如图,在平面直角坐标系中,二次函数的图象交坐标轴于A(﹣1,0),B(4,0),C(0,﹣4)三点,点P是直线BC下方抛物线上一动点.
(1)求这个二次函数的解析式;
(2)是否存在点P,使△POC是以OC为底边的等腰三角形?若存在,求出P点坐标;若不存在,请说明理由;
(3)动点P运动到什么位置时,△PBC面积最大,求出此时P点坐标和△PBC的最大面积.
解:
(1)设抛物线解析式为y=ax2+bx+c,
把A、B、C三点坐标代入可得,解得,
∴抛物线解析式为y=x2﹣3x﹣4;
(2)作OC的垂直平分线DP,交OC于点D,交BC下方抛物线于点P,如图1,
∴PO=PC,此时P点即为满足条件的点,
∵C(0,﹣4),
∴D(0,﹣2),
∴P点纵坐标为﹣2,
代入抛物线解析式可得x2﹣3x﹣4=﹣2,解得x=(小于0,舍去)或x=,
∴存在满足条件的P点,其坐标为(,﹣2);
(3)∵点P在抛物线上,
∴可设P(t,t2﹣3t﹣4),
过P作PE⊥x轴于点E,交直线BC于点F,如图2,
∵B(4,0),C(0,﹣4),
∴直线BC解析式为y=x﹣4,
∴F(t,t﹣4),
∴PF=(t﹣4)﹣(t2﹣3t﹣4)=﹣t2+4t,
∴S△PBC=S△PFC+S△PFB=PF?OE+PF?BE=PF?(OE+BE)=PF?OB=(﹣t2+4t)×4=﹣2(t﹣2)2+8,
∴当t=2时,S△PBC最大值为8,此时t2﹣3t﹣4=﹣6,
∴当P点坐标为(2,﹣6)时,△PBC的最大面积为8.
八、(本题满分14分)
23.通过类比联想、引申拓展研究典型题目,可以达到解一题知一类题的目的.下面是一个案例,请补充完整.
原题;如图①,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,试说明理由.
(1)【思路梳理】
∵AB=AD,∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合,∵∠ADG=∠B=90°,∴∠FDG=180°,即:点F、D、G共线,根据“SAS”,易证△AFG≌ △AFE ,得EF=FG=BE+DF;
(2)【类比引申】
如图②,四边形ABCD中,AB=AD,∠BAD=90°,点E、F分别在BC、CD上,∠EAF=45°,若∠B,∠D都不是直角,则当∠B与∠D满足等量关系 ∠B+∠D=180° 时,仍有EF=BE+DF;
(3)【联想拓展】
如图③,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°,猜想BD,DE,EC应满足的等量关系,并写出推理过程.
解:(1)如图1,∵四边形ABCD是正方形,
∴AB=AD,∠B=∠BAD=∠ADC=90°,
把△ABE绕点A逆时针旋转90°到△ADG,则∠DAG=∠BAE,AG=AE,
∵∠ADG=∠B=90°,
∴∠ADC+∠ADG=180°,
∴点F、D、G在同一条直线上;
∵∠EAF=45°,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=90°﹣45°=45°,
∴∠GAF=∠EAF,
∵AF=AF,
∴△AFG≌△AFE(SAS),
∴EF=GF=DG+DF=BE+DF,
故答案为:△AFE.
(2)如图2,由题意得,AB=AD,∠BAD=90°,
把△ABE绕点A逆时针旋转90°到△ADG,则∠DAG=∠BAE,∠ADG=∠B,AG=AE,
当∠B+∠ADC=180°,即∠B+∠D=180°时,则∠ADG+∠ADC=180°,
∴点F、D、G在同一条直线上;
∵∠EAF=45°,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=90°﹣45°=45°,
∴∠GAF=∠EAF,
∵AF=AF,
∴△AFG≌△AFE(SAS),
∴EF=GF=DG+DF=BE+DF,
故答案为:∠B+∠D=180°.
(3)DE2=BD2+EC2,
证明:如图3,由题意得,AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°;
把△ABD绕点A逆时针旋转90°到△ACG,则∠CAG=∠BAD,∠ACG=∠B=45°,AG=AD,CG=BD,
∴∠ECG=∠ACB+∠ACG=90°;
∵∠DAE=45°,
∵∠GAE=∠CAG+∠CAE=∠BAD+∠CAE=90°﹣45°=45°,
∴∠GAE=∠DAE,
∵AE=AE,
∴△AEG≌△AED(SAS),
∴GE=DE,
∵GE2=CG2+EC2,
∴DE2=BD2+EC2.
同课章节目录
