湖南省长沙市长沙县2020-2021学年高二下学期期末考试数学试题 (Word版含答案)
文档属性
| 名称 | 湖南省长沙市长沙县2020-2021学年高二下学期期末考试数学试题 (Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 235.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-22 11:12:43 | ||
图片预览


文档简介
长沙县2020-2021学年高二下学期期末考试
数
学
本试题卷共4页,分第Ⅰ卷与第Ⅱ卷两部分,全卷满分150分,考试用时120分钟.
第Ⅰ卷(选择题共60分)
一、选择题:本大题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知全集U={2,4,6,8,10},集合A={2,4},则(
)
A.{2,4}
B.{6,8,10}
C.{2,4,6,8}
D.{2,4,6,8,10}
2.截一个几何体,所得各截面都是圆面,则这个几何体一定是(
)
A.圆柱
B.圆锥
C.球
D.圆台
3.函数与关于(
)对称.
A.x轴
B.y轴
C.
D.原点
4.从某超市抽取13袋袋装食用盐,对其质量(单位:g)进行统计,得到如图所示的茎叶图.若从这13袋食用盐中随机选取1袋,则该袋食用盐的质量在[499,501]内的概率为(
)
A.
B.
C.
D.
5.△ABC中,若a=1,c=2,B=30°,则△ABC的面积为(
)
A.
B.
C.1
D.
6.某校一个课外学习小组为研究某作物种子的发芽率y和温度x(单位:℃)的关系,在20个不同的温度条件下进行种子发芽实验,由实验数据(xi,yi)(i=1,2,…,20)得到下面的散点图:
由此散点图,在10℃至40℃之间,下面四个回归方程类型中最适宜作为发芽率y和温度x的回归方程类型的是(
)
A.
B.
C.
D.
7.设l1,l2,l3是三条不同的直线,α,β,γ是三个不同的平面,则下列命题是真命题的是(
)
A.若l1∥α,α∥l2,则l1∥l2
B.若l1⊥α,l2⊥α,则l1⊥l2
C.若l1∥l2,,,,则l1∥l3
D.若α⊥β,,,则l1∥l2
8.已知从甲袋内摸出1个红球的概率是,从乙袋内摸出1个红球的概率是,从两袋内各摸出1个球,则等于(
)
A.2个球不都是红球的概率
B.2个球都是红球的概率
C.2个球中至少有1个红球的概率
D.2个球中恰好有1个红球的概率
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.
9.已知,,且,则(
)
A.
B.
C.
D.
10.已知离散型随机变量X的分布列如下表,则(
)
X
0
1
P
A.
B.
C.
D.
11.如图所示,四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD,则下列结论中正确的是(
)
A.AC
⊥
SB
B.AB∥平面SCD
C.SA与平面SBD所成的角等于SC与平面SBD所成的角
D.AB与SC所成的角等于DC与SA所成的角
12.已知函数,下列命题正确的是(
)
A.的最小正周期为
B.在区间(0,)上为增函数
C.直线是函数图象的一条对称轴;
D.函数的图象可由函数的图象向右平移个单位长度得到
第Ⅱ卷(非选择题共90分)
三、填空题:本大题共4小题,每小题5分,共20分。
13.函数(,且)恒过一个定点,则该点的坐标为________.
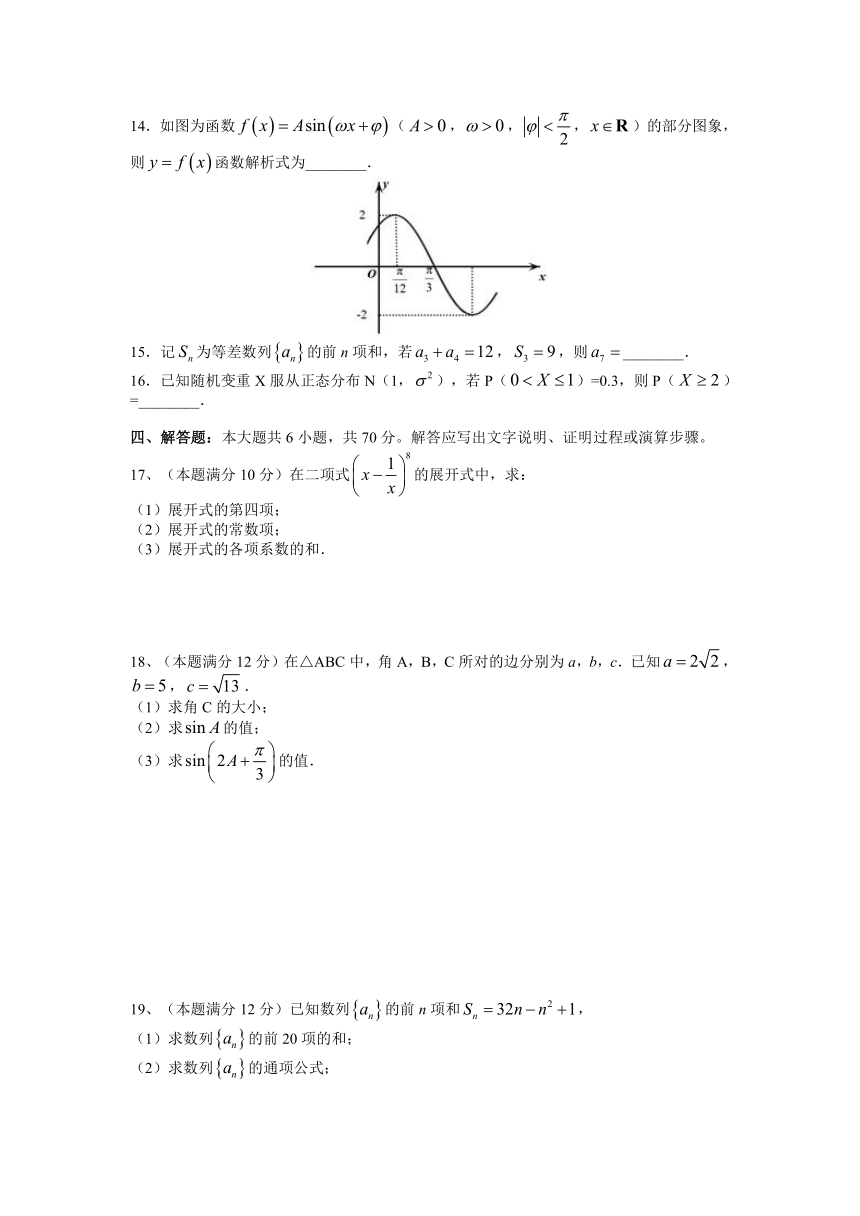
14.如图为函数(,,,)的部分图象,则函数解析式为________.
15.记为等差数列的前n项和,若,,则________.
16.已知随机变重X服从正态分布N(1,),若P()=0.3,则P()=________.
四、解答题:本大题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17、(本题满分10分)在二项式的展开式中,求:
(1)展开式的第四项;
(2)展开式的常数项;
(3)展开式的各项系数的和.
18、(本题满分12分)在△ABC中,角A,B,C所对的边分别为a,b,c.已知,
,.
(1)求角C的大小;
(2)求的值;
(3)求的值.
19、(本题满分12分)已知数列的前n项和,
(1)求数列的前20项的和;
(2)求数列的通项公式;
(3)求数列的前多少项和最大.
20、(本题满分12分)已知圆C:(,)与x轴,y轴分
别相切于A,B两点.
(1)求圆C的方程;
(2)若直线l:与线段AB没有公共点,求实数k的取值范围;
(3)试讨论直线l:与圆C:(,)的位置关系.
21、(本题满分12分)设a是实数,.
(1)试证明对于任意a,为增函数;
(2)试确定a值,使为奇函数.
22、(本题满分12分)微信是现代生活信息交流的重要工具,随机对使用微信的100人进行统计,得到如下数据统计表,每天使用微信时间在两小时以上的人被定义为“微信依赖”,不超过两小时的人被定义为“非微信依赖”,已知“非微信依赖”与“微信依赖”人数比恰为3:2.
使用微信时间(单位:小时)
(0,0.5]
(0.5,1]
(1,1.5]
(1.5,2]
(2,2.5]
(2.5,3]
合计
频数
5
15
15
x
30
y
100
频率
0.05
0.15
0.15
p
0.30
q
1.00
(1)确定x,y,p,q的值;
(2)为进一步了解使用微信对自己的日常工作和生活是否有影响,从“微信依赖”和“非微信依赖”的100人中用分层随机抽样的方法确定10人,若需从这10人中随机选取3人进行问卷调查,设选取的3人中“微信依赖”的人数为X,求X的分布列;
(3)求(2)中选取的3人中“微信依赖”至少2人的概率.
2021年高中二年二期期末检测试卷
数
学
参考答案
一、选择题:本大题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
题号
1
2
3
4
5
6
7
8
答案
B
C
B
B
A
D
C
C
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得3分.
题号
9
10
11
12
答案
ABD
ABC
ABC
BC
三、填空题:本大题共4小题,每小题5分,共20分。
13、(1,3)
14、
15、13
16、0.2
四、解答题:本大题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.(本小题满分10分)(1)展开式的第四项为;
(2)展开式的常数项为70;
(3)展开式的各项系数的和0.
18、(本小题满分12分)(1)
(2)
(3)
19、(本小题满分12分)(1)数列的前20项的和为241;
(2)数列的通项公式为;
(3)数列的前16项和最大,最大为257.
20、(本小题满分12分)(1)圆C的方程为:
(2)实数k的取值范围为(,1)
(3)由C(2,2)到直线的距离,解得
由图可知,当(,)时,直线l与圆C相离;
当时时,直线l与圆C相切;
当(,)时,直线l与圆C相交.
21、(本小题满分12分)解:(1)证明:设x1、x2∈R且x1<x2,
,
又由在R上为增函数,则>0,>0,
由x1<x2,可得<0,则<0,
故为增函数,与a的值无关,
即对于任意a,在R为增函数;
(2)若f(x)为奇函数,且其定义域为R,必有,
即,变形可得
解可得,a=1,
即当a=1时,为奇函数.
22、(本小题满分12分)(1)x=25,y=10,p=0.25,q=0.10.
(2)用分层抽样的方法确定的10人中,“非微信依赖”有10×=6人,“微信依赖”有4人.
随机变量X的取值为0,1,2,3,
P(X=0)=,
P(X=1)=,
P(X=2)=,
P(X=3)=,
∴X的分布列为
X
0
1
2
3
P
(3)选取的3人中“微信依赖”至少2人分2种情况:选取的3人中“微信依赖”有2人和3人,分别对应(2)中的P(X=2),P(X=3),
故所求事件的概率为P=P(X=2)+P(X=3)=+=.
数
学
本试题卷共4页,分第Ⅰ卷与第Ⅱ卷两部分,全卷满分150分,考试用时120分钟.
第Ⅰ卷(选择题共60分)
一、选择题:本大题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知全集U={2,4,6,8,10},集合A={2,4},则(
)
A.{2,4}
B.{6,8,10}
C.{2,4,6,8}
D.{2,4,6,8,10}
2.截一个几何体,所得各截面都是圆面,则这个几何体一定是(
)
A.圆柱
B.圆锥
C.球
D.圆台
3.函数与关于(
)对称.
A.x轴
B.y轴
C.
D.原点
4.从某超市抽取13袋袋装食用盐,对其质量(单位:g)进行统计,得到如图所示的茎叶图.若从这13袋食用盐中随机选取1袋,则该袋食用盐的质量在[499,501]内的概率为(
)
A.
B.
C.
D.
5.△ABC中,若a=1,c=2,B=30°,则△ABC的面积为(
)
A.
B.
C.1
D.
6.某校一个课外学习小组为研究某作物种子的发芽率y和温度x(单位:℃)的关系,在20个不同的温度条件下进行种子发芽实验,由实验数据(xi,yi)(i=1,2,…,20)得到下面的散点图:
由此散点图,在10℃至40℃之间,下面四个回归方程类型中最适宜作为发芽率y和温度x的回归方程类型的是(
)
A.
B.
C.
D.
7.设l1,l2,l3是三条不同的直线,α,β,γ是三个不同的平面,则下列命题是真命题的是(
)
A.若l1∥α,α∥l2,则l1∥l2
B.若l1⊥α,l2⊥α,则l1⊥l2
C.若l1∥l2,,,,则l1∥l3
D.若α⊥β,,,则l1∥l2
8.已知从甲袋内摸出1个红球的概率是,从乙袋内摸出1个红球的概率是,从两袋内各摸出1个球,则等于(
)
A.2个球不都是红球的概率
B.2个球都是红球的概率
C.2个球中至少有1个红球的概率
D.2个球中恰好有1个红球的概率
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.
9.已知,,且,则(
)
A.
B.
C.
D.
10.已知离散型随机变量X的分布列如下表,则(
)
X
0
1
P
A.
B.
C.
D.
11.如图所示,四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD,则下列结论中正确的是(
)
A.AC
⊥
SB
B.AB∥平面SCD
C.SA与平面SBD所成的角等于SC与平面SBD所成的角
D.AB与SC所成的角等于DC与SA所成的角
12.已知函数,下列命题正确的是(
)
A.的最小正周期为
B.在区间(0,)上为增函数
C.直线是函数图象的一条对称轴;
D.函数的图象可由函数的图象向右平移个单位长度得到
第Ⅱ卷(非选择题共90分)
三、填空题:本大题共4小题,每小题5分,共20分。
13.函数(,且)恒过一个定点,则该点的坐标为________.
14.如图为函数(,,,)的部分图象,则函数解析式为________.
15.记为等差数列的前n项和,若,,则________.
16.已知随机变重X服从正态分布N(1,),若P()=0.3,则P()=________.
四、解答题:本大题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17、(本题满分10分)在二项式的展开式中,求:
(1)展开式的第四项;
(2)展开式的常数项;
(3)展开式的各项系数的和.
18、(本题满分12分)在△ABC中,角A,B,C所对的边分别为a,b,c.已知,
,.
(1)求角C的大小;
(2)求的值;
(3)求的值.
19、(本题满分12分)已知数列的前n项和,
(1)求数列的前20项的和;
(2)求数列的通项公式;
(3)求数列的前多少项和最大.
20、(本题满分12分)已知圆C:(,)与x轴,y轴分
别相切于A,B两点.
(1)求圆C的方程;
(2)若直线l:与线段AB没有公共点,求实数k的取值范围;
(3)试讨论直线l:与圆C:(,)的位置关系.
21、(本题满分12分)设a是实数,.
(1)试证明对于任意a,为增函数;
(2)试确定a值,使为奇函数.
22、(本题满分12分)微信是现代生活信息交流的重要工具,随机对使用微信的100人进行统计,得到如下数据统计表,每天使用微信时间在两小时以上的人被定义为“微信依赖”,不超过两小时的人被定义为“非微信依赖”,已知“非微信依赖”与“微信依赖”人数比恰为3:2.
使用微信时间(单位:小时)
(0,0.5]
(0.5,1]
(1,1.5]
(1.5,2]
(2,2.5]
(2.5,3]
合计
频数
5
15
15
x
30
y
100
频率
0.05
0.15
0.15
p
0.30
q
1.00
(1)确定x,y,p,q的值;
(2)为进一步了解使用微信对自己的日常工作和生活是否有影响,从“微信依赖”和“非微信依赖”的100人中用分层随机抽样的方法确定10人,若需从这10人中随机选取3人进行问卷调查,设选取的3人中“微信依赖”的人数为X,求X的分布列;
(3)求(2)中选取的3人中“微信依赖”至少2人的概率.
2021年高中二年二期期末检测试卷
数
学
参考答案
一、选择题:本大题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
题号
1
2
3
4
5
6
7
8
答案
B
C
B
B
A
D
C
C
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得3分.
题号
9
10
11
12
答案
ABD
ABC
ABC
BC
三、填空题:本大题共4小题,每小题5分,共20分。
13、(1,3)
14、
15、13
16、0.2
四、解答题:本大题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.(本小题满分10分)(1)展开式的第四项为;
(2)展开式的常数项为70;
(3)展开式的各项系数的和0.
18、(本小题满分12分)(1)
(2)
(3)
19、(本小题满分12分)(1)数列的前20项的和为241;
(2)数列的通项公式为;
(3)数列的前16项和最大,最大为257.
20、(本小题满分12分)(1)圆C的方程为:
(2)实数k的取值范围为(,1)
(3)由C(2,2)到直线的距离,解得
由图可知,当(,)时,直线l与圆C相离;
当时时,直线l与圆C相切;
当(,)时,直线l与圆C相交.
21、(本小题满分12分)解:(1)证明:设x1、x2∈R且x1<x2,
,
又由在R上为增函数,则>0,>0,
由x1<x2,可得<0,则<0,
故为增函数,与a的值无关,
即对于任意a,在R为增函数;
(2)若f(x)为奇函数,且其定义域为R,必有,
即,变形可得
解可得,a=1,
即当a=1时,为奇函数.
22、(本小题满分12分)(1)x=25,y=10,p=0.25,q=0.10.
(2)用分层抽样的方法确定的10人中,“非微信依赖”有10×=6人,“微信依赖”有4人.
随机变量X的取值为0,1,2,3,
P(X=0)=,
P(X=1)=,
P(X=2)=,
P(X=3)=,
∴X的分布列为
X
0
1
2
3
P
(3)选取的3人中“微信依赖”至少2人分2种情况:选取的3人中“微信依赖”有2人和3人,分别对应(2)中的P(X=2),P(X=3),
故所求事件的概率为P=P(X=2)+P(X=3)=+=.
同课章节目录
