湖南省长沙市长沙县2020-2021学年高一下学期期末考试数学试题 (Word版含答案)
文档属性
| 名称 | 湖南省长沙市长沙县2020-2021学年高一下学期期末考试数学试题 (Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 237.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-22 11:13:32 | ||
图片预览


文档简介
长沙县2020-2021学年高一下学期期末考试
数
学
本试题卷共4页,分第Ⅰ卷与第Ⅱ卷两部分,全卷满分150分,考试用时120分钟.
第Ⅰ卷(选择题共60分)
一、选择题:本大题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.的虚部是(
)
A.
B.
C.
D.2
2.设,是两个平面向量,则“”是“”的(
)
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
3.水平放置的ABC的直观图如图,其中B'O'=C'O'=1,A'O'=,那么原△
ABC
是一个
三角形.(
)
A.等边
B.三边互不相等的
C.三边中只有两边相等的等腰
D.直角
4.从1,2,3,…,10这10个数中,任取3个数,那么“这3个数的和不大于8”这一事件包含的样本点的个数是(
)
A.4
B.5
C.6
D.7
5.我国古代数学名若《九章算术》有一抽样问题:“今有北乡若千人,西乡七千四百八十八人,南乡六千九百一十二人,凡三乡,发役三百人,而北乡需遣一百零八人,问北乡人数几何?”其意思为:“今有某地北面若千人,西面有7488人,南面有6912人,这三面要征调300人,而北面共征调108人(用样本量比例分配的分层随机抽样方法),则北面共有多少人(
)
A.8000
B.8100
C.8200
D.8300
6.已知,是单位向量,且,则(
)
A.
B.
C.
D.与的夹角为
7.袋内有红、白、黑球各为3,2,1个,从中任取2个,则互斥而不对立的两个事件是(
)A.至少有一个白球;都是白球
B.至少有一个白球;至少有一个红球
C.恰有一个白球;一个白球一个黑球
D.至少有一个白球;红、黑球各一个
8.设m,n为两条不同的直线,α为平面,则下列结论正确的是(
)
A.m⊥n,m∥α?n⊥α
B.m⊥n,m⊥α?n∥α
C.m∥n,m⊥α?n⊥α
D.m∥n,m∥α=n∥α
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.
9.已知D,E,F分别为△ABC的边BC,CA,AB的中点,且,,给出下列结论,其中正确的有(
)
A.
B.
C.
D.
10.下列说法正确的有(
)
A.对任意的事件A,都有P(A)>0
B.随机事件A发生的概率是频率的稳定值,频率是概率的近似值
C.必然事件的概率为1,不可能事件的概率为0
D.若事件事件B,则
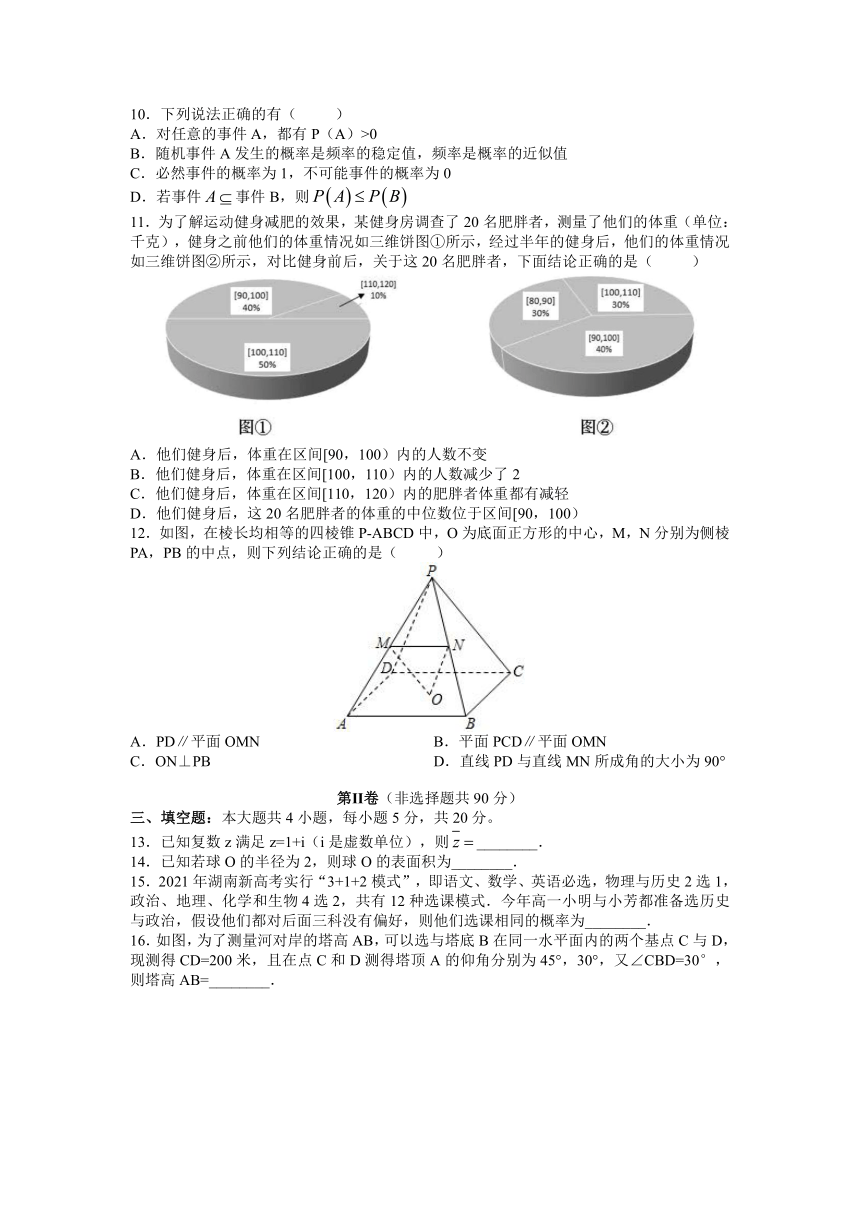
11.为了解运动健身减肥的效果,某健身房调查了20名肥胖者,测量了他们的体重(单位:千克),健身之前他们的体重情况如三维饼图①所示,经过半年的健身后,他们的体重情况如三维饼图②所示,对比健身前后,关于这20名肥胖者,下面结论正确的是(
)
A.他们健身后,体重在区间[90,100)内的人数不变
B.他们健身后,体重在区间[100,110)内的人数减少了2
C.他们健身后,体重在区间[110,120)内的肥胖者体重都有减轻
D.他们健身后,这20名肥胖者的体重的中位数位于区间[90,100)
12.如图,在棱长均相等的四棱锥P-ABCD中,O为底面正方形的中心,M,N分别为侧棱PA,PB的中点,则下列结论正确的是(
)
A.PD∥平面OMN
B.平面PCD∥平面OMN
C.ON⊥PB
D.直线PD与直线MN所成角的大小为90°
第Ⅱ卷(非选择题共90分)
三、填空题:本大题共4小题,每小题5分,共20分。
13.已知复数z满足z=1+i(i是虚数单位),则________.
14.已知若球O的半径为2,则球O的表面积为________.
15.2021年湖南新高考实行“3+1+2模式”,即语文、数学、英语必选,物理与历史2选1,政治、地理、化学和生物4选2,共有12种选课模式.今年高一小明与小芳都准备选历史与政治,假设他们都对后面三科没有偏好,则他们选课相同的概率为________.
16.如图,为了测量河对岸的塔高AB,可以选与塔底B在同一水平面内的两个基点C与D,
现测得CD=200米,且在点C和D测得塔顶A的仰角分别为45°,30°,又∠CBD=30°,则塔高AB=________.
四、解答题:本大题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17、(本题满分10分)若复数(),复数.
(1)求;
(2)若,求实数a的值;
(3)若a=2,求.
18、(本题满分12分)已知向量=(,1),=(1,),,.
(1)求;
(2)若,求k的值;
(3)当k=1时,求与夹角的余弦值.
19、(本题满分12分)在△ABC中,角A,B,C所对的边分别为a,b,c.已知,
,.
(1)求角C的大小;
(2)求的值;
(3)求的值.
20、(本题满分12分)某城市交通部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照[50,60),[60,70),….[90,100]分成5组,制成如图所示频率分直方图.
(1)求图中x的值;
(2)求这组数据的平均数和中位数;
(3)已知满意度评分值在[50,60)内的男生数与女生数的比为3:2,若在满意度评分值为[50,60)的人中随机抽取2人进行座谈,求2人均为男生的概率.
21、(本题满分12分)甲、乙两人各射击一次,击中目标的概率分别是,.假设两人
射击是否击中目标相互之间没有影响,每人每次射击是否击中目标相互之间也没有影响.
(1)若甲、乙两人各射击一次,求均没有击中目标的概率;
(2)若甲连续射击,命中为止,求甲恰好射击3次结束射击的概率;
(3)若乙连续射击,直至命中2次为止,求乙恰好射击3次结束射击的概率.
22、(本题满分12分)如图,在三棱柱ABC-A1B1C1中,△ABC与△A1B1C1都为正三角形,且AA1⊥面ABC,F,F1分别是AC,A1C1的中点、求证:
(1)
AF1∥FC1;
(2)平面AB1F1∥平面C1BF;
(3)平面AB1F1⊥平面ACC1A1.
2021年高中一年二期期末检测试卷
数
学
参考答案
一、选择题:本大题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
题号
1
2
3
4
5
6
7
8
答案
B
A
A
A
B
B
D
C
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得3分.
题号
9
10
11
12
答案
AC
BCD
ACD
ABC
三、填空题:本大题共4小题,每小题5分,共20分。
13、
14、
15、
16、200
m
四、解答题:本大题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.(本小题满分10分)(1)
(2)∵z1+z2=1+ai+3-4i=4+(a-4)i
又∵
∴a-4=0,即a=4
(3)
18、(本小题满分12分)(1)=(,)
(2)
(3)当k=1时,求与夹角的余弦值为
19、(本小题满分12分)(1)
(2)
(3)
20、(本小题满分12分)解:(1)由0.005+0.01+0.035+0.030+x)×10=1,
解得x=0.02.
(2)这组数据的平均数为55×0.05+65×0.2+75×0.35+85×0.3+95×0.1=77.
中位数设为m,则0.05+0.2+(m-70)×0.035=0.5,
解得m=
(3)满意度评分值在[50,60)内有100×0.005×10=5人,
其中男生3人,女生2人.记为A1,A2,A3,B1,B2,记“满意度评分值为[50,60)的人中随机抽取2人进行座谈,2人均为男生”为事件A
总基本事件个数为n==10个,
A包含的基本事件个数为3个,分别为:(A1,A2),(A1,A3),(A2,A3),
利用古典概型概率公式可知2人均为男生的概率P(A)=
21、(本小题满分12分)(1)若甲、乙两人各射击一次,求均没有击中目标的概率为P(甲)=,P(乙)=;
(2)若甲连续射击,命中为止,求甲恰好射击3次结束射击的概率为;
(3)若乙连续射击,直至命中2次为止,求乙恰好射击3次结束射击的概率为
.
22、(本小题满分12分)(1)在正三棱柱ABC-A1B1C1中,
∵F、F1分别是AC、A1C1的中点,
∴B1F1∥BF,AF1∥C1F.
(2)由(1)可知B1F1∥BF,AF1∥C1F
又∵B1F1∩AF1=F1,C1F∩BF=F,
∴平面AB1F1∥平面C1BF.
(3)在三棱柱ABC-A1B1C1中,AA1⊥平面A1B1C1,∴B1F1⊥AA1.
又B1F1⊥A1C1,A1C1∩AA1=A1,
∴B1F1⊥平面ACC1A1,而B1F1?平面AB1F1,
∴平面AB1F1⊥平面ACC1A1.
数
学
本试题卷共4页,分第Ⅰ卷与第Ⅱ卷两部分,全卷满分150分,考试用时120分钟.
第Ⅰ卷(选择题共60分)
一、选择题:本大题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.的虚部是(
)
A.
B.
C.
D.2
2.设,是两个平面向量,则“”是“”的(
)
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
3.水平放置的ABC的直观图如图,其中B'O'=C'O'=1,A'O'=,那么原△
ABC
是一个
三角形.(
)
A.等边
B.三边互不相等的
C.三边中只有两边相等的等腰
D.直角
4.从1,2,3,…,10这10个数中,任取3个数,那么“这3个数的和不大于8”这一事件包含的样本点的个数是(
)
A.4
B.5
C.6
D.7
5.我国古代数学名若《九章算术》有一抽样问题:“今有北乡若千人,西乡七千四百八十八人,南乡六千九百一十二人,凡三乡,发役三百人,而北乡需遣一百零八人,问北乡人数几何?”其意思为:“今有某地北面若千人,西面有7488人,南面有6912人,这三面要征调300人,而北面共征调108人(用样本量比例分配的分层随机抽样方法),则北面共有多少人(
)
A.8000
B.8100
C.8200
D.8300
6.已知,是单位向量,且,则(
)
A.
B.
C.
D.与的夹角为
7.袋内有红、白、黑球各为3,2,1个,从中任取2个,则互斥而不对立的两个事件是(
)A.至少有一个白球;都是白球
B.至少有一个白球;至少有一个红球
C.恰有一个白球;一个白球一个黑球
D.至少有一个白球;红、黑球各一个
8.设m,n为两条不同的直线,α为平面,则下列结论正确的是(
)
A.m⊥n,m∥α?n⊥α
B.m⊥n,m⊥α?n∥α
C.m∥n,m⊥α?n⊥α
D.m∥n,m∥α=n∥α
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得2分.
9.已知D,E,F分别为△ABC的边BC,CA,AB的中点,且,,给出下列结论,其中正确的有(
)
A.
B.
C.
D.
10.下列说法正确的有(
)
A.对任意的事件A,都有P(A)>0
B.随机事件A发生的概率是频率的稳定值,频率是概率的近似值
C.必然事件的概率为1,不可能事件的概率为0
D.若事件事件B,则
11.为了解运动健身减肥的效果,某健身房调查了20名肥胖者,测量了他们的体重(单位:千克),健身之前他们的体重情况如三维饼图①所示,经过半年的健身后,他们的体重情况如三维饼图②所示,对比健身前后,关于这20名肥胖者,下面结论正确的是(
)
A.他们健身后,体重在区间[90,100)内的人数不变
B.他们健身后,体重在区间[100,110)内的人数减少了2
C.他们健身后,体重在区间[110,120)内的肥胖者体重都有减轻
D.他们健身后,这20名肥胖者的体重的中位数位于区间[90,100)
12.如图,在棱长均相等的四棱锥P-ABCD中,O为底面正方形的中心,M,N分别为侧棱PA,PB的中点,则下列结论正确的是(
)
A.PD∥平面OMN
B.平面PCD∥平面OMN
C.ON⊥PB
D.直线PD与直线MN所成角的大小为90°
第Ⅱ卷(非选择题共90分)
三、填空题:本大题共4小题,每小题5分,共20分。
13.已知复数z满足z=1+i(i是虚数单位),则________.
14.已知若球O的半径为2,则球O的表面积为________.
15.2021年湖南新高考实行“3+1+2模式”,即语文、数学、英语必选,物理与历史2选1,政治、地理、化学和生物4选2,共有12种选课模式.今年高一小明与小芳都准备选历史与政治,假设他们都对后面三科没有偏好,则他们选课相同的概率为________.
16.如图,为了测量河对岸的塔高AB,可以选与塔底B在同一水平面内的两个基点C与D,
现测得CD=200米,且在点C和D测得塔顶A的仰角分别为45°,30°,又∠CBD=30°,则塔高AB=________.
四、解答题:本大题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17、(本题满分10分)若复数(),复数.
(1)求;
(2)若,求实数a的值;
(3)若a=2,求.
18、(本题满分12分)已知向量=(,1),=(1,),,.
(1)求;
(2)若,求k的值;
(3)当k=1时,求与夹角的余弦值.
19、(本题满分12分)在△ABC中,角A,B,C所对的边分别为a,b,c.已知,
,.
(1)求角C的大小;
(2)求的值;
(3)求的值.
20、(本题满分12分)某城市交通部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照[50,60),[60,70),….[90,100]分成5组,制成如图所示频率分直方图.
(1)求图中x的值;
(2)求这组数据的平均数和中位数;
(3)已知满意度评分值在[50,60)内的男生数与女生数的比为3:2,若在满意度评分值为[50,60)的人中随机抽取2人进行座谈,求2人均为男生的概率.
21、(本题满分12分)甲、乙两人各射击一次,击中目标的概率分别是,.假设两人
射击是否击中目标相互之间没有影响,每人每次射击是否击中目标相互之间也没有影响.
(1)若甲、乙两人各射击一次,求均没有击中目标的概率;
(2)若甲连续射击,命中为止,求甲恰好射击3次结束射击的概率;
(3)若乙连续射击,直至命中2次为止,求乙恰好射击3次结束射击的概率.
22、(本题满分12分)如图,在三棱柱ABC-A1B1C1中,△ABC与△A1B1C1都为正三角形,且AA1⊥面ABC,F,F1分别是AC,A1C1的中点、求证:
(1)
AF1∥FC1;
(2)平面AB1F1∥平面C1BF;
(3)平面AB1F1⊥平面ACC1A1.
2021年高中一年二期期末检测试卷
数
学
参考答案
一、选择题:本大题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
题号
1
2
3
4
5
6
7
8
答案
B
A
A
A
B
B
D
C
二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得3分.
题号
9
10
11
12
答案
AC
BCD
ACD
ABC
三、填空题:本大题共4小题,每小题5分,共20分。
13、
14、
15、
16、200
m
四、解答题:本大题共6小题,共70分。解答应写出文字说明、证明过程或演算步骤。
17.(本小题满分10分)(1)
(2)∵z1+z2=1+ai+3-4i=4+(a-4)i
又∵
∴a-4=0,即a=4
(3)
18、(本小题满分12分)(1)=(,)
(2)
(3)当k=1时,求与夹角的余弦值为
19、(本小题满分12分)(1)
(2)
(3)
20、(本小题满分12分)解:(1)由0.005+0.01+0.035+0.030+x)×10=1,
解得x=0.02.
(2)这组数据的平均数为55×0.05+65×0.2+75×0.35+85×0.3+95×0.1=77.
中位数设为m,则0.05+0.2+(m-70)×0.035=0.5,
解得m=
(3)满意度评分值在[50,60)内有100×0.005×10=5人,
其中男生3人,女生2人.记为A1,A2,A3,B1,B2,记“满意度评分值为[50,60)的人中随机抽取2人进行座谈,2人均为男生”为事件A
总基本事件个数为n==10个,
A包含的基本事件个数为3个,分别为:(A1,A2),(A1,A3),(A2,A3),
利用古典概型概率公式可知2人均为男生的概率P(A)=
21、(本小题满分12分)(1)若甲、乙两人各射击一次,求均没有击中目标的概率为P(甲)=,P(乙)=;
(2)若甲连续射击,命中为止,求甲恰好射击3次结束射击的概率为;
(3)若乙连续射击,直至命中2次为止,求乙恰好射击3次结束射击的概率为
.
22、(本小题满分12分)(1)在正三棱柱ABC-A1B1C1中,
∵F、F1分别是AC、A1C1的中点,
∴B1F1∥BF,AF1∥C1F.
(2)由(1)可知B1F1∥BF,AF1∥C1F
又∵B1F1∩AF1=F1,C1F∩BF=F,
∴平面AB1F1∥平面C1BF.
(3)在三棱柱ABC-A1B1C1中,AA1⊥平面A1B1C1,∴B1F1⊥AA1.
又B1F1⊥A1C1,A1C1∩AA1=A1,
∴B1F1⊥平面ACC1A1,而B1F1?平面AB1F1,
∴平面AB1F1⊥平面ACC1A1.
同课章节目录
