2021-2022学年人教版七年级上 册4.3.3余角与补角课件(共17张PPT)
文档属性
| 名称 | 2021-2022学年人教版七年级上 册4.3.3余角与补角课件(共17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 266.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-23 16:40:06 | ||
图片预览






文档简介
(共17张PPT)
观赏意大利名胜比萨斜塔
1
2
1
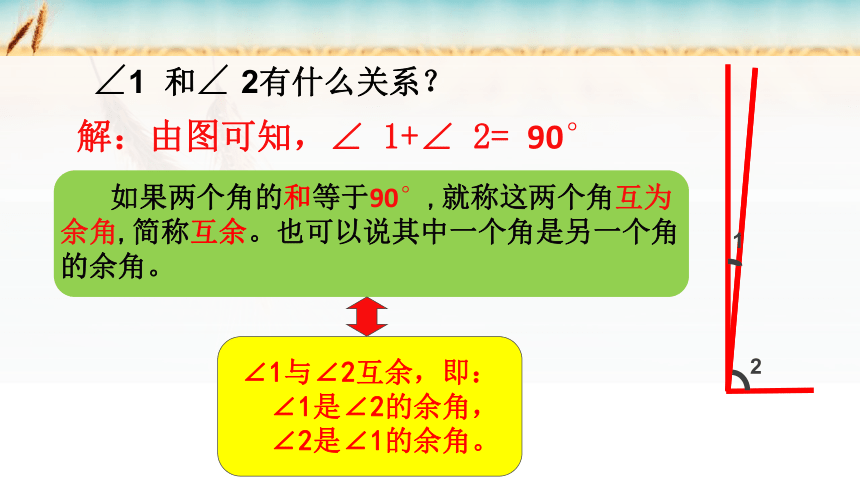
和
2有什么关系?
3
4
3和
4有什么关系?
老师寄语:
学好数学关键在于思考。看似枯燥无味的数学公式,细心品味其内涵与外延,也能触摸到深刻的美丽。
4.3.3
余角和补角
1.理解余角和补角的定义和性质。
2.会运用互余、互补的关系进行运算。
3.掌握方位角的辨别与应用。
学习目标
请同学们认真看P137-138的内容,思考:
1.在课本中划出余角与补角的概念,结合图形理解这两个概念.
2.思考如何求一个角的余角与补角.
3.重点看例3的解题步骤,理解余角和补角的性质
(在课本划出这两个性质)
4.例4的方位角怎么定义的?
自学指导(5分钟)
2
1
1
和
2有什么关系?
如果两个角的和等于90°,就称这两个角互为余角,简称互余。也可以说其中一个角是另一个角的余角。
解:由图可知,∠
1+∠
2=
90°
∠1与∠2互余,即:
∠1是∠2的余角,
∠2是∠1的余角。
4
3
3和
4有什么关系?
解:由图可知,∠
3+∠
4
=
180°
如果两个角的和等于180°,就称这两个角互为补角,简称互补。也可以说其中一个角是另一个角的补角。
∠1与∠2互补,即:
∠1是∠2的补角,
∠2是∠1的补角。
1、图中给出的各角,哪些互为余角?(连一连)
10o
30o
60o
80o
50o
40o
检测练习一
(抢答)
30o
60o
80o
100o
120o
150o
2、图中给出的各角,哪些互为补角?(连一连)
检测练习一
(抢答)
3.已知∠1+∠2=
,∠1+∠3=
,
如果∠2=
,则∠3=
。
检测练习一
60
同角的余角相等
想一想:已知∠1+∠2=
,∠3+∠4=
,
如果∠1=∠3,∠2=
,则∠4=
。
30°
30°
60°
等角的余角相等
余角的性质:同角(等角)的余角相等
4.已知∠1+∠2=
,∠1+∠3=
,
如果∠2=
,则∠3=
。
检测练习一
70°
同角的补角相等
80°
等角的补角相等
补角的性质:同角(等角)的补角相等
想一想:已知∠1+∠2=
,∠3+∠4=
,
如果∠1=∠3,∠2=
,则∠4=
。
80°
70°
检测练习二
(抢答)
1、求出
的余角与补角。
30°
60°
150°
想一想:同一个角的余角与它的补角之间有怎样的数量关系?
一个角的补角比它的余角
大
。
90°
45°
135°
10°
100°
90°—α
180°—α
α
2、如图,OA表示北偏东32°方向线,
OB表示南偏东43°方向
线,则∠AOB等于————。
105°
检测练习二
方位角
方位角是表示方向的角,通常以正北、正南方向为角的始边,以对象所处的射线为终边,描述方位角时,先描述北或南,再叙述偏东或偏西。
必做题
1.20°+
=90°,20°+
=180°
已知∠1=20°,则∠1的余角=
,∠1的补角=
。
当堂作业
70°
160°
70°
160°
2、A看B的方向是北偏东30°,那么B看A的方向是(
)
A、南偏东60°
B、南偏西60°
C、南偏东30°
D、南偏西30°
D
A
东
北
东
北
1
2
B
3.一个角是30°20′
,求它的余角和补角。
解:90°-
30°20′=
59°40′
180°-
30°20′=
149°40′
答:
它的余角和补角分别是59°40′,149°40′。
4、已知一个角的补角是它的3倍,这个角是多少度?
解:设这个角是
x°
,则它的补角是3
x°,依题意得
3x
=180°
—
x
解得:x
=
45°
答:这个角是
45°.
5、如图,已知AOB是一直线,OC是∠
AOB的平分线,
∠
DOE是直角,图中哪些角互余?哪些角互补?哪些角相等?
思考题:
A
O
B
E
C
D
1
2
3
4
观赏意大利名胜比萨斜塔
1
2
1
和
2有什么关系?
3
4
3和
4有什么关系?
老师寄语:
学好数学关键在于思考。看似枯燥无味的数学公式,细心品味其内涵与外延,也能触摸到深刻的美丽。
4.3.3
余角和补角
1.理解余角和补角的定义和性质。
2.会运用互余、互补的关系进行运算。
3.掌握方位角的辨别与应用。
学习目标
请同学们认真看P137-138的内容,思考:
1.在课本中划出余角与补角的概念,结合图形理解这两个概念.
2.思考如何求一个角的余角与补角.
3.重点看例3的解题步骤,理解余角和补角的性质
(在课本划出这两个性质)
4.例4的方位角怎么定义的?
自学指导(5分钟)
2
1
1
和
2有什么关系?
如果两个角的和等于90°,就称这两个角互为余角,简称互余。也可以说其中一个角是另一个角的余角。
解:由图可知,∠
1+∠
2=
90°
∠1与∠2互余,即:
∠1是∠2的余角,
∠2是∠1的余角。
4
3
3和
4有什么关系?
解:由图可知,∠
3+∠
4
=
180°
如果两个角的和等于180°,就称这两个角互为补角,简称互补。也可以说其中一个角是另一个角的补角。
∠1与∠2互补,即:
∠1是∠2的补角,
∠2是∠1的补角。
1、图中给出的各角,哪些互为余角?(连一连)
10o
30o
60o
80o
50o
40o
检测练习一
(抢答)
30o
60o
80o
100o
120o
150o
2、图中给出的各角,哪些互为补角?(连一连)
检测练习一
(抢答)
3.已知∠1+∠2=
,∠1+∠3=
,
如果∠2=
,则∠3=
。
检测练习一
60
同角的余角相等
想一想:已知∠1+∠2=
,∠3+∠4=
,
如果∠1=∠3,∠2=
,则∠4=
。
30°
30°
60°
等角的余角相等
余角的性质:同角(等角)的余角相等
4.已知∠1+∠2=
,∠1+∠3=
,
如果∠2=
,则∠3=
。
检测练习一
70°
同角的补角相等
80°
等角的补角相等
补角的性质:同角(等角)的补角相等
想一想:已知∠1+∠2=
,∠3+∠4=
,
如果∠1=∠3,∠2=
,则∠4=
。
80°
70°
检测练习二
(抢答)
1、求出
的余角与补角。
30°
60°
150°
想一想:同一个角的余角与它的补角之间有怎样的数量关系?
一个角的补角比它的余角
大
。
90°
45°
135°
10°
100°
90°—α
180°—α
α
2、如图,OA表示北偏东32°方向线,
OB表示南偏东43°方向
线,则∠AOB等于————。
105°
检测练习二
方位角
方位角是表示方向的角,通常以正北、正南方向为角的始边,以对象所处的射线为终边,描述方位角时,先描述北或南,再叙述偏东或偏西。
必做题
1.20°+
=90°,20°+
=180°
已知∠1=20°,则∠1的余角=
,∠1的补角=
。
当堂作业
70°
160°
70°
160°
2、A看B的方向是北偏东30°,那么B看A的方向是(
)
A、南偏东60°
B、南偏西60°
C、南偏东30°
D、南偏西30°
D
A
东
北
东
北
1
2
B
3.一个角是30°20′
,求它的余角和补角。
解:90°-
30°20′=
59°40′
180°-
30°20′=
149°40′
答:
它的余角和补角分别是59°40′,149°40′。
4、已知一个角的补角是它的3倍,这个角是多少度?
解:设这个角是
x°
,则它的补角是3
x°,依题意得
3x
=180°
—
x
解得:x
=
45°
答:这个角是
45°.
5、如图,已知AOB是一直线,OC是∠
AOB的平分线,
∠
DOE是直角,图中哪些角互余?哪些角互补?哪些角相等?
思考题:
A
O
B
E
C
D
1
2
3
4
