5.2 平面直角坐标系 课件(共33张PPT)
文档属性
| 名称 | 5.2 平面直角坐标系 课件(共33张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-22 19:30:39 | ||
图片预览







文档简介
(共33张PPT)
第五章
位置与坐标
2
平面直角三角形
知识点一
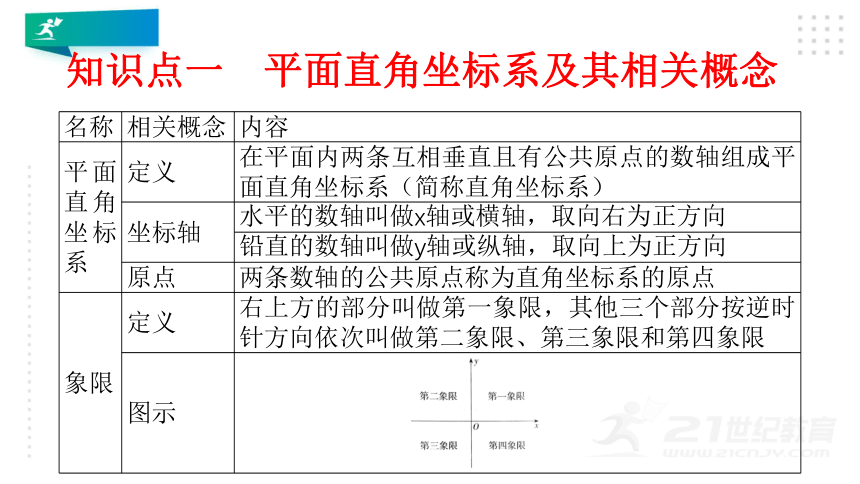
平面直角坐标系及其相关概念
名称
相关概念
内容
平面直角坐标系
定义
在平面内两条互相垂直且有公共原点的数轴组成平面直角坐标系(简称直角坐标系)
坐标轴
水平的数轴叫做x轴或横轴,取向右为正方向
铅直的数轴叫做y轴或纵轴,取向上为正方向
原点
两条数轴的公共原点称为直角坐标系的原点
象限
定义
右上方的部分叫做第一象限,其他三个部分按逆时针方向依次叫做第二象限、第三象限和第四象限
图示
?
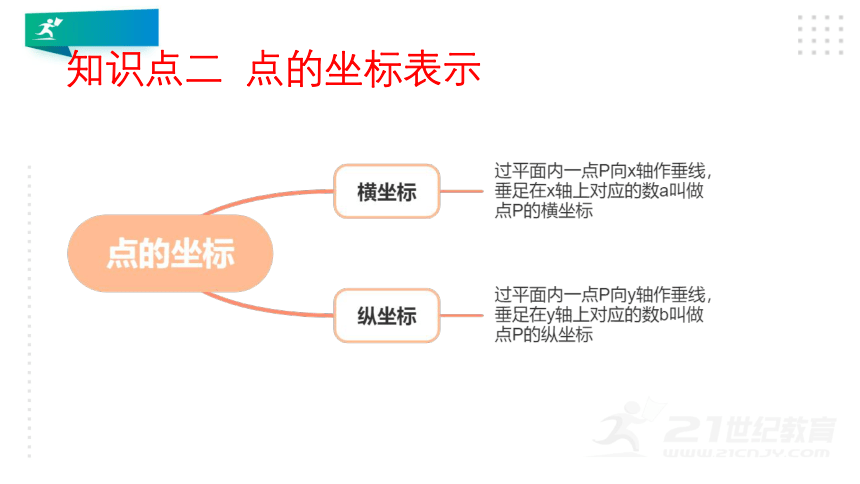
知识点二
点的坐标表示
温馨提示
(1)点的坐标(a,b)中a,b的顺序不能颠倒,先横坐标后纵坐标,(b,a)与(a,b)表示不同的两个点的坐标(此时a≠b).
(2)在直角坐标系中,对于平面上的任意一点,都有唯一的一对有序实数对(即点的坐标)与它对应;反过来,对于任意一对有序实数对,都有平面上唯一的一点与它对应.
例1
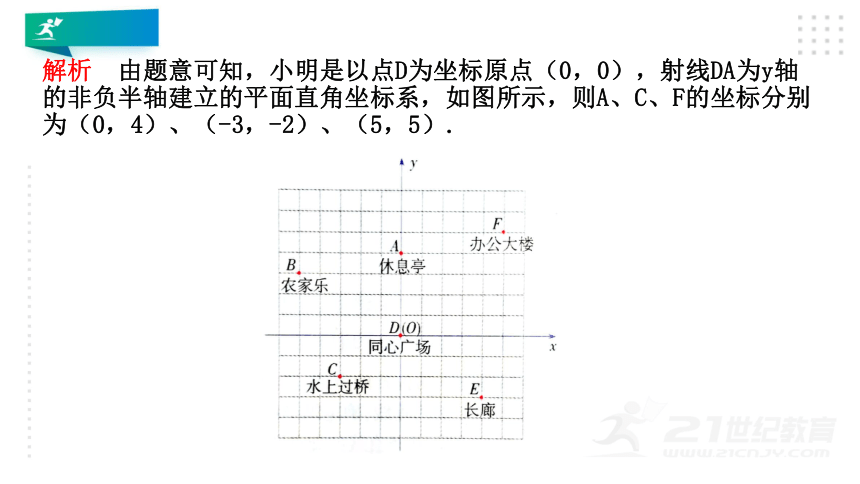
小明和爸爸、妈妈到白银水川湿地公园游玩,回到家后,他利用平面直角坐标系画出了公园的景区地图,如图所示.可是他忘记了在图中标出原点、x轴及y轴只知道长廊E的坐标为(4,-3)和农家乐B的坐标为(-5,3),请你帮他画出平面直角坐标系,并写出其他各点的坐标.
解析
由题意可知,小明是以点D为坐标原点(0,0),射线DA为y轴的非负半轴建立的平面直角坐标系,如图所示,则A、C、F的坐标分别为(0,4)、(-3,-2)、(5,5).
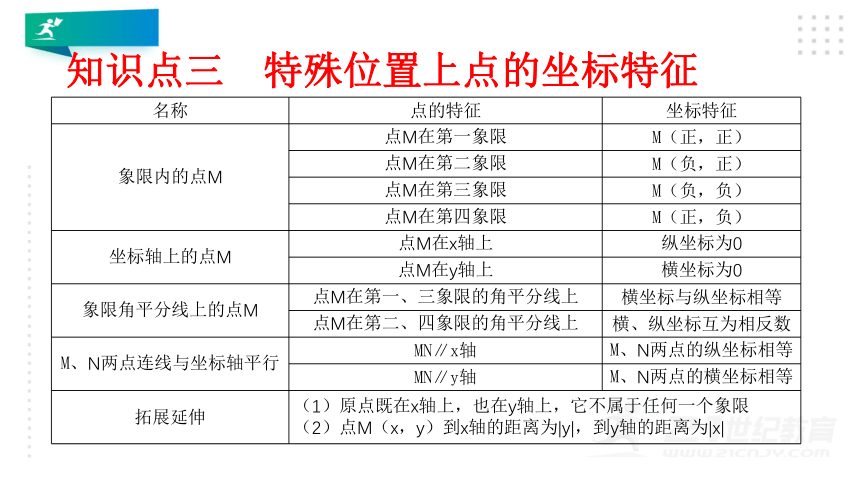
知识点三
特殊位置上点的坐标特征
名称
点的特征
坐标特征
象限内的点M
点M在第一象限
M(正,正)
点M在第二象限
M(负,正)
点M在第三象限
M(负,负)
点M在第四象限
M(正,负)
坐标轴上的点M
点M在x轴上
纵坐标为0
点M在y轴上
横坐标为0
象限角平分线上的点M
点M在第一、三象限的角平分线上
横坐标与纵坐标相等
点M在第二、四象限的角平分线上
横、纵坐标互为相反数
M、N两点连线与坐标轴平行
MN∥x轴
M、N两点的纵坐标相等
MN∥y轴
M、N两点的横坐标相等
拓展延伸
(1)原点既在x轴上,也在y轴上,它不属于任何一个象限
(2)点M(x,y)到x轴的距离为|y|,到y轴的距离为|x|
例2
若点P(a,b)满足a2b>0,则点P所在的象限为(
)
A.第一象限或第二象限
B.第一象限或第四象限
C.第二象限或第三象限
D.第三象限或第四象限
例2
若点P(a,b)满足a2b>0,则点P所在的象限为(
)
A.第一象限或第二象限
B.第一象限或第四象限
C.第二象限或第三象限
D.第三象限或第四象限
解析
因为a2b>0,所以b>0,a>0或a<0,
当a>0,b>0时,点P所在的象限为第一象限;
当a<0,b>0时,点P所在的象限为第二象限,
故选A.
例2
若点P(a,b)满足a2b>0,则点P所在的象限为(
A
)
A.第一象限或第二象限
B.第一象限或第四象限
C.第二象限或第三象限
D.第三象限或第四象限
解析
因为a2b>0,所以b>0,a>0或a<0,
当a>0,b>0时,点P所在的象限为第一象限;
当a<0,b>0时,点P所在的象限为第二象限,
故选A.
知识点四
由点的坐标确定点的位置继而确定图形的形状
已知点的坐标确定点的位置的方法:确定横坐标在x轴上的位置,过该点作x轴的垂线;确定纵坐标在y轴上的位置,过该点作y轴的垂线,两条直线的交点即为所求.
例3
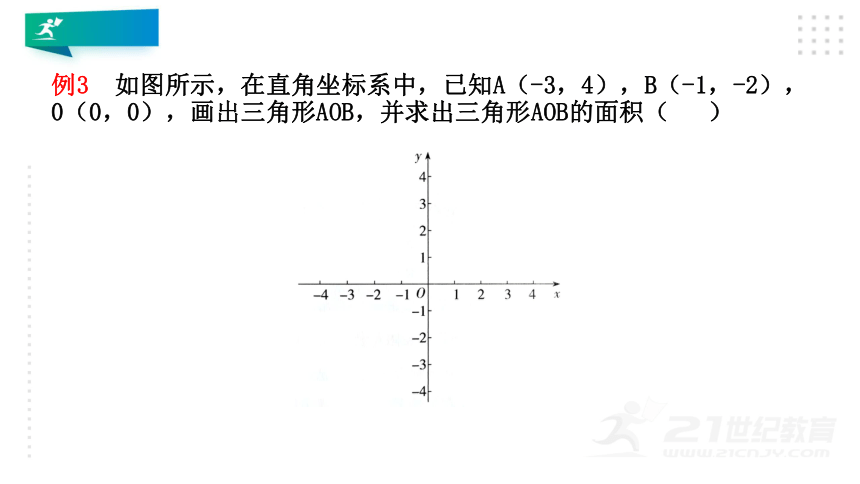
如图所示,在直角坐标系中,已知A(-3,4),B(-1,-2),0(0,0),画出三角形AOB,并求出三角形AOB的面积(
)
知识点五
建立平面直角坐标系,确定点的坐标
建立直角坐标系
步骤
技巧
知识点五
建立平面直角坐标系,确定点的坐标
建立直角坐标系
步骤
分析条件,选择适当的一点作为坐标原点
过原点找或作两个互相垂直的直线,分别作为x轴和y轴
确定正方向和单位长度
技巧
知识点五
建立平面直角坐标系,确定点的坐标
建立直角坐标系
步骤
分析条件,选择适当的一点作为坐标原点
过原点找或作两个互相垂直的直线,分别作为x轴和y轴
确定正方向和单位长度
技巧
使图形中尽量多的点在坐标轴上;以某些特殊线段所在的直线为x轴或y轴;以轴对称图形的对称轴为x轴或y轴;以某已知点为原点
例4
如图所示,△ABC是边长为2的等边三角形,建立适当的直角坐标系写出各个顶点的坐标.
分析
以边BC的中点为坐标原点,以边BC所在的直线为x轴,以边BC的垂直平分线为y轴,建立平面直角坐标系,这样各顶点的坐标表示较简单.
点拨
根据已知条件建立适当的坐标系是确定点的位置的必经过程,只有建立适当的坐标系,点的位置才能得以确定,才能使数与形有机地结合起来.
经典例题
题型一
根据点的位置确定点的坐标
例1
在平面直角坐标系xOy中,点P(x,y)在第二象限,且点P到横轴的距离等于3,到纵轴的距离等于4,则点P坐标是(
)
A.(-3,4)
B.(3,-4)
C.(-4,3)
D.(4,-3)
题型一
根据点的位置确定点的坐标
解析
∵点P在第二象限,且第二象限内的点横坐标小于0,纵坐标大于0,
∴点P的横坐标小于0,纵坐标大于0.
∵点P到x轴的距离等于3,到y轴的距离等于4,
∴点P的坐标是(-4,3).
、
题型一
根据点的位置确定点的坐标
解析
∵点P在第二象限,且第二象限内的点横坐标小于0,纵坐标大于0,
∴点P的横坐标小于0,纵坐标大于0.
∵点P到x轴的距离等于3,到y轴的距离等于4,
∴点P的坐标是(-4,3).
故选C.
题型一
根据点的位置确定点的坐标
点拨
掌握点的坐标的几何意义是解题关键,点到x轴的距离为点的纵坐标的绝对值,到y轴的距离为点的横坐标的绝对值,再结合第二象限内点的坐标特征即可确定P点坐标.
题型二
根据已知点的位置求字母的值(或范围)
题型二
根据已知点的位置求字母的值(或范围)
题型二
根据已知点的位置求字母的值(或范围)
例3
若点M(a+3,2a-1)在y轴上,则a的值是__________.
例3
若点M(a+3,2a-1)在y轴上,则a的值是__________.
解析
∵点M(a+3,2a-1)在y轴上,∴a+3=0,解得a=-3.
故答案为-3.
例3
若点M(a+3,2a-1)在y轴上,则a的值是__________.
解析
∵点M(a+3,2a-1)在y轴上,∴a+3=0,解得a=-3.
故答案为-3.
点拨
掌握点的坐标与点到坐标轴的距离的关系是解题的关键.
第五章
位置与坐标
2
平面直角三角形
知识点一
平面直角坐标系及其相关概念
名称
相关概念
内容
平面直角坐标系
定义
在平面内两条互相垂直且有公共原点的数轴组成平面直角坐标系(简称直角坐标系)
坐标轴
水平的数轴叫做x轴或横轴,取向右为正方向
铅直的数轴叫做y轴或纵轴,取向上为正方向
原点
两条数轴的公共原点称为直角坐标系的原点
象限
定义
右上方的部分叫做第一象限,其他三个部分按逆时针方向依次叫做第二象限、第三象限和第四象限
图示
?
知识点二
点的坐标表示
温馨提示
(1)点的坐标(a,b)中a,b的顺序不能颠倒,先横坐标后纵坐标,(b,a)与(a,b)表示不同的两个点的坐标(此时a≠b).
(2)在直角坐标系中,对于平面上的任意一点,都有唯一的一对有序实数对(即点的坐标)与它对应;反过来,对于任意一对有序实数对,都有平面上唯一的一点与它对应.
例1
小明和爸爸、妈妈到白银水川湿地公园游玩,回到家后,他利用平面直角坐标系画出了公园的景区地图,如图所示.可是他忘记了在图中标出原点、x轴及y轴只知道长廊E的坐标为(4,-3)和农家乐B的坐标为(-5,3),请你帮他画出平面直角坐标系,并写出其他各点的坐标.
解析
由题意可知,小明是以点D为坐标原点(0,0),射线DA为y轴的非负半轴建立的平面直角坐标系,如图所示,则A、C、F的坐标分别为(0,4)、(-3,-2)、(5,5).
知识点三
特殊位置上点的坐标特征
名称
点的特征
坐标特征
象限内的点M
点M在第一象限
M(正,正)
点M在第二象限
M(负,正)
点M在第三象限
M(负,负)
点M在第四象限
M(正,负)
坐标轴上的点M
点M在x轴上
纵坐标为0
点M在y轴上
横坐标为0
象限角平分线上的点M
点M在第一、三象限的角平分线上
横坐标与纵坐标相等
点M在第二、四象限的角平分线上
横、纵坐标互为相反数
M、N两点连线与坐标轴平行
MN∥x轴
M、N两点的纵坐标相等
MN∥y轴
M、N两点的横坐标相等
拓展延伸
(1)原点既在x轴上,也在y轴上,它不属于任何一个象限
(2)点M(x,y)到x轴的距离为|y|,到y轴的距离为|x|
例2
若点P(a,b)满足a2b>0,则点P所在的象限为(
)
A.第一象限或第二象限
B.第一象限或第四象限
C.第二象限或第三象限
D.第三象限或第四象限
例2
若点P(a,b)满足a2b>0,则点P所在的象限为(
)
A.第一象限或第二象限
B.第一象限或第四象限
C.第二象限或第三象限
D.第三象限或第四象限
解析
因为a2b>0,所以b>0,a>0或a<0,
当a>0,b>0时,点P所在的象限为第一象限;
当a<0,b>0时,点P所在的象限为第二象限,
故选A.
例2
若点P(a,b)满足a2b>0,则点P所在的象限为(
A
)
A.第一象限或第二象限
B.第一象限或第四象限
C.第二象限或第三象限
D.第三象限或第四象限
解析
因为a2b>0,所以b>0,a>0或a<0,
当a>0,b>0时,点P所在的象限为第一象限;
当a<0,b>0时,点P所在的象限为第二象限,
故选A.
知识点四
由点的坐标确定点的位置继而确定图形的形状
已知点的坐标确定点的位置的方法:确定横坐标在x轴上的位置,过该点作x轴的垂线;确定纵坐标在y轴上的位置,过该点作y轴的垂线,两条直线的交点即为所求.
例3
如图所示,在直角坐标系中,已知A(-3,4),B(-1,-2),0(0,0),画出三角形AOB,并求出三角形AOB的面积(
)
知识点五
建立平面直角坐标系,确定点的坐标
建立直角坐标系
步骤
技巧
知识点五
建立平面直角坐标系,确定点的坐标
建立直角坐标系
步骤
分析条件,选择适当的一点作为坐标原点
过原点找或作两个互相垂直的直线,分别作为x轴和y轴
确定正方向和单位长度
技巧
知识点五
建立平面直角坐标系,确定点的坐标
建立直角坐标系
步骤
分析条件,选择适当的一点作为坐标原点
过原点找或作两个互相垂直的直线,分别作为x轴和y轴
确定正方向和单位长度
技巧
使图形中尽量多的点在坐标轴上;以某些特殊线段所在的直线为x轴或y轴;以轴对称图形的对称轴为x轴或y轴;以某已知点为原点
例4
如图所示,△ABC是边长为2的等边三角形,建立适当的直角坐标系写出各个顶点的坐标.
分析
以边BC的中点为坐标原点,以边BC所在的直线为x轴,以边BC的垂直平分线为y轴,建立平面直角坐标系,这样各顶点的坐标表示较简单.
点拨
根据已知条件建立适当的坐标系是确定点的位置的必经过程,只有建立适当的坐标系,点的位置才能得以确定,才能使数与形有机地结合起来.
经典例题
题型一
根据点的位置确定点的坐标
例1
在平面直角坐标系xOy中,点P(x,y)在第二象限,且点P到横轴的距离等于3,到纵轴的距离等于4,则点P坐标是(
)
A.(-3,4)
B.(3,-4)
C.(-4,3)
D.(4,-3)
题型一
根据点的位置确定点的坐标
解析
∵点P在第二象限,且第二象限内的点横坐标小于0,纵坐标大于0,
∴点P的横坐标小于0,纵坐标大于0.
∵点P到x轴的距离等于3,到y轴的距离等于4,
∴点P的坐标是(-4,3).
、
题型一
根据点的位置确定点的坐标
解析
∵点P在第二象限,且第二象限内的点横坐标小于0,纵坐标大于0,
∴点P的横坐标小于0,纵坐标大于0.
∵点P到x轴的距离等于3,到y轴的距离等于4,
∴点P的坐标是(-4,3).
故选C.
题型一
根据点的位置确定点的坐标
点拨
掌握点的坐标的几何意义是解题关键,点到x轴的距离为点的纵坐标的绝对值,到y轴的距离为点的横坐标的绝对值,再结合第二象限内点的坐标特征即可确定P点坐标.
题型二
根据已知点的位置求字母的值(或范围)
题型二
根据已知点的位置求字母的值(或范围)
题型二
根据已知点的位置求字母的值(或范围)
例3
若点M(a+3,2a-1)在y轴上,则a的值是__________.
例3
若点M(a+3,2a-1)在y轴上,则a的值是__________.
解析
∵点M(a+3,2a-1)在y轴上,∴a+3=0,解得a=-3.
故答案为-3.
例3
若点M(a+3,2a-1)在y轴上,则a的值是__________.
解析
∵点M(a+3,2a-1)在y轴上,∴a+3=0,解得a=-3.
故答案为-3.
点拨
掌握点的坐标与点到坐标轴的距离的关系是解题的关键.
