2021-2022学年粤教版(2019)选择性必修第三册 2.1气体实验定律(Ⅰ)同步作业(word解析版)
文档属性
| 名称 | 2021-2022学年粤教版(2019)选择性必修第三册 2.1气体实验定律(Ⅰ)同步作业(word解析版) |

|
|
| 格式 | doc | ||
| 文件大小 | 621.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-08-22 00:00:00 | ||
图片预览



文档简介
2021-2022学年粤教版(2019)选择性必修第三册
2.1气体实验定律(Ⅰ)同步作业(解析版)
1.如图所示,在光滑水平面上,一质量为m的导热活塞将一定质量的理想气体封闭在内壁光滑的圆柱形气缸中,开始时活塞和气缸静止,此时气柱长度为l,现使气缸底部绕一竖直轴由静止开始转动,缓慢增大转动的角速度,当气缸转动的角速度为1时,气柱长度为2l,当气缸转动的角速度为2时,气柱长度为3l,若外界大气压不变,则1与2的比值为( )
A.
B.
C.2:3
D.3:2
2.如图所示,竖直放置的粗细相同的玻璃管A、B底部由橡皮软管连接,橡皮管内充满水银。一定质量的空气被水银柱封闭在A管内。B管上方与大气相通。初始时两管水银面向平。A管固定不动,环境温度不变的情况下,为使A管内水银面上升,则应缓慢( )
A.上移B管
B.下移B管
C.右移B管
D.左移B管
3.容积V=10L的钢瓶充满氧后,压强p=20atm,打开钢瓶盖阀门,让氧气分别装到容积为V0=5L的小瓶子中去,若小瓶子已抽成真空,分装到小瓶子中的氧气压强均为p0=2atm。在分装过程中无漏气现象,且温度保持不变,那么最多可装的瓶数是( )
A.2瓶
B.18瓶
C.0.10瓶
D.20瓶
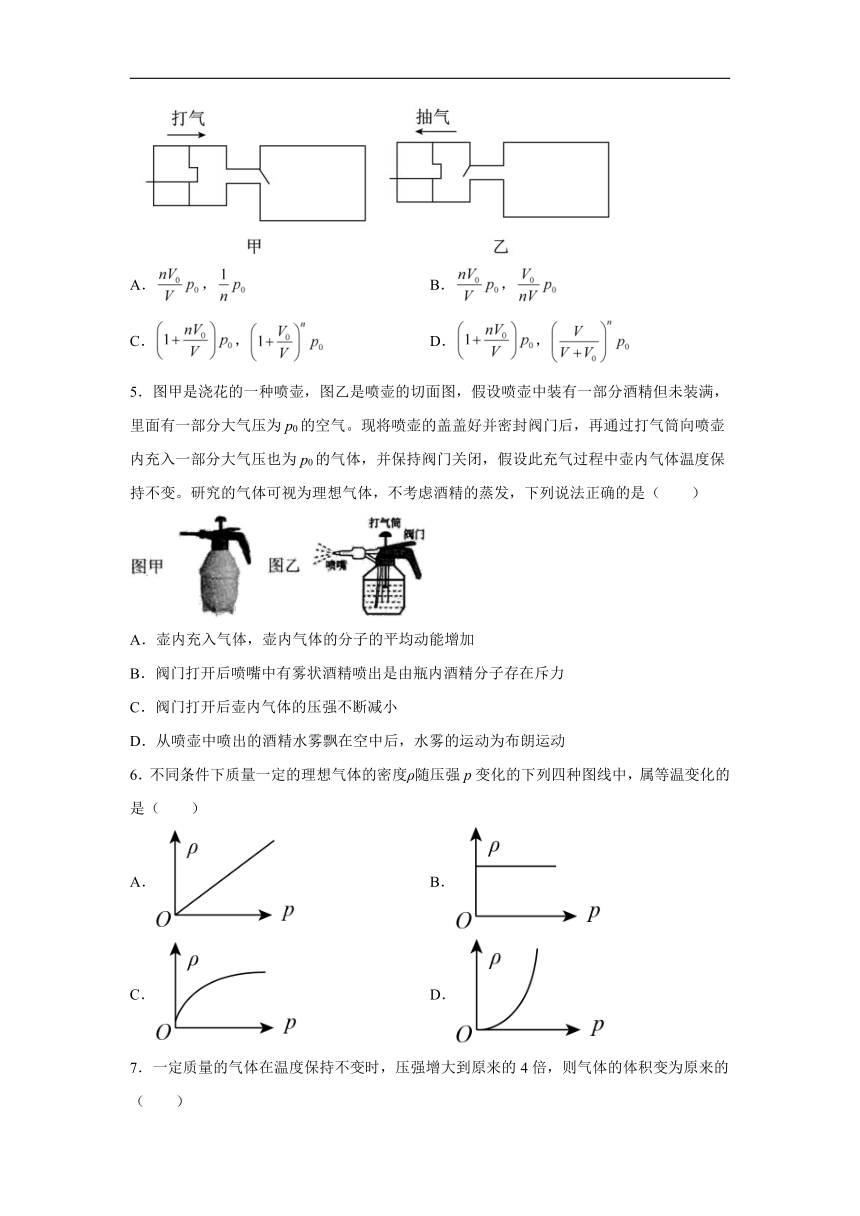
4.只两用活塞气筒的原理如图所示(打气时如图甲,抽气时如图乙),其筒内体积为V0,现将它与另一只容积为V的容器相连接,气筒和容器内的空气压强为p0,已知气筒和容器导热性能良好,当分别作为打气筒和抽气筒时,活塞工作n次后,在上述两种情况下,容器内的气体压强分别为( )
A.,
B.,
C.,
D.,
5.图甲是浇花的一种喷壶,图乙是喷壶的切面图,假设喷壶中装有一部分酒精但未装满,里面有一部分大气压为p0的空气。现将喷壶的盖盖好并密封阀门后,再通过打气筒向喷壶内充入一部分大气压也为p0的气体,并保持阀门关闭,假设此充气过程中壶内气体温度保持不变。研究的气体可视为理想气体,不考虑酒精的蒸发,下列说法正确的是( )
A.壶内充入气体,壶内气体的分子的平均动能增加
B.阀门打开后喷嘴中有雾状酒精喷出是由瓶内酒精分子存在斥力
C.阀门打开后壶内气体的压强不断减小
D.从喷壶中喷出的酒精水雾飘在空中后,水雾的运动为布朗运动
6.不同条件下质量一定的理想气体的密度ρ随压强p变化的下列四种图线中,属等温变化的是( )
A.
B.
C.
D.
7.一定质量的气体在温度保持不变时,压强增大到原来的4倍,则气体的体积变为原来的( )
A.4
B.2
C.
D.
8.现从一体积不变的容器中抽气,假设温度保持不变,每一次抽气后,容器内气体的压强均减小到原来的,要使容器内剩余气体的压强减为原来的,抽气次数应为( )
A.2次
B.3次
C.4次
D.5次
9.如图所示,两端封闭的形管中,初始时连接处有一段水银将气体分为、两部分,现打开阀门一段时间后关闭,期间无水银漏出,则关闭阀门后气体的体积相比初始时( )
A.增大
B.减小
C.不变
D.无法判断
10.有一段12cm长水银柱,在均匀玻璃管中封住一定质量的气体。若将玻璃管管口向上放置在一个倾角为30°的斜面上(如图所示),先用外力使玻璃管静止在斜面上,后由静止释放,玻璃管沿斜面下滑。已知玻璃管与斜面间的动摩擦因数为,大气压强p0相当于76cm汞柱,气体温度不变。则下列说法正确的是( )
A.释放后气体体积变大
B.释放后气体体积变小
C.下滑稳定时密闭气体的压强为80cm汞柱
D.下滑稳定时密闭气体的压强为79cm汞柱
11.如图所示,有一重力可以忽略的薄壁小试管开口向下竖直地浮在很大的水银槽内,试管中有一长为h1的水银柱封住两段气体A、B,A、B气柱长分别为l1、l2,管内外水银面高度差为h2,在保持温度不变的情况下,下列说法正确的是( )
A.开始时h2一定等于h1
B.若外界大气压缓慢增加少许,则h2不变,l1变小,l2变小
C.若外界大气压缓慢增加少许,则h2变小,l1变大,l2变大
D.若用手轻按试管,使试管竖直向下移少许,则h2变大,l1变小,l2变小
12.如图所示,图线1和2分别表示一定质量的气体在不同温度下的等温线。下列说法正确的是( )
A.气体由状态A沿图线1变化到状态B的过程中,分子间平均距离减小
B.图线1对应的温度低于图线2
C.图线1对应的温度高于图线2
D.气体由状态A沿图线1变化到状态B的过程中,气体分子的平均速率不变
13.如图所示,1m左右的玻璃管内,水银柱上面封闭一段气体,管内外水银面的高度差为h=72cm,大气压强为76cmHg,下列说法正确的是( )
A.将管稍微上提,h不变
B.将管稍微上提,h变大
C.将管下插至管顶与管外水银面高度差为70cm时,管内外水银面高度差也是70cm
D.将管下插至管顶与管外水银面高度差为70cm时,管内外水银面高度差小于70cm
14.如图所示,D→A→B→C表示一定质量的某种气体状态变化的一个过程。则下列说法正确的是( )
A.D→A是一个等温过程
B.A→B是一个等温过程
C.A与B的各状态参量均相同
D.B→C体积增大,压强减小,温度不变
15.如图所示的装置,气缸分上、下两部分,下部分的横截面积大于上部分的横截面积,大小活塞分别在上、下气缸内用一根硬杆相连,两活塞可在气缸内一起上下移动。缸内封有一定质量的气体,活塞与缸壁无摩擦且不漏气。初始时,活塞处于静止态,小活塞上的杯子里放有大量钢球。在列哪些情况下,两活塞将相对气缸向下移动( )
A.给气缸内气体援慢加热
B.大气压变小
C.减少几个钢球
D.让整个装置自由落体
16.在如图所示的机械式取水装置中,活塞从阀门处开始往上移动时,阀门开启,活塞向下移动时,阀门关闭,空气从活塞处溢出,地下水就通过直管被抽上来,地下水位线距离阀门的高度H=40m,用力向上拉活塞到某位置,使直管中水缓慢上升h=5m,然后活塞关闭。已知水的密度ρ=1.0×103kg/m3,外界大气压强p0=1.0×105Pa,重力加速度g=10m/s?,直管中的气体可视为理想气体,抽水过程直管中的空气温度不变。求:
(1)直管中水上升后管内气体压强p的大小;
(2)阀门关闭后,求阀门下方直管中剩余空气质量△m与直管中原空气质量m0的比值。
17.如图所示,粗细均匀的等高U形玻璃管竖直放置,左管封闭,右端开口,用水银柱封闭长为的一段空气柱,右侧水银柱比左侧高出,已知大气压为。现用一质量不计的薄活塞封住右端开口,缓慢向下压活塞使两边液面相平,此过程中环境温度始终不变,当两边液面相平时,求:
(1)左侧空气柱的压强。
(2)右侧空气柱的长度多少厘米?(计算结果保留两位小数)
18.如图,开口向上的气缸内盛有一定深度的水银,一粗细均匀,长为l=24cm且下端开口的细玻管竖直漂浮在水银中。平衡时,玻管露出水银面的高度和进入玻管中的水银柱长度均为h1=6cm,轻质活塞到水银面的高度为h0=12cm,水银面上方的气体压强为p0=76
cm
Hg。现施外力使活塞缓慢向下移动,当玻管上端恰好与水银面齐平时,进入玻管中的水银柱长度为h2=12cm。活塞与气缸壁间的摩擦不计且密封性良好,玻管的横截面积远小于气缸的横截面积,整个过程中各部分气体的温度保持不变,求:
(1)玻管上端恰好与水银面齐平时,玻管内气体的压强;
(2)整个过程中活塞向下移动的距离。
19.如图所示,竖直圆简是固定不动的,粗筒横截面积是细筒的2倍,细筒足够长粗筒中A、B两轻质活塞间封有一定质量的空气(可视为理想气体),气柱长。活塞A上方的水银深,两活塞的重力及与筒壁间的摩擦不计,用外力向上托住活塞B使之处于平衡状态,水银面与粗筒上端相平现使活塞B缓慢上移,直至水银的三分之二被推入细筒中,求活塞B上移的距离。(设在整个过程中气柱的温度不变,大气压强当于的水银柱产生的压强)
20.如图所示是小明学习完热学内容后设计的一个测量小车加速度的简易装置。在车上水平固定内壁光滑且导热的气缸,缸内有一定质量的空气(可视为理想气体〕,被质量为m且厚度不计的活塞分隔成Ⅰ、Ⅱ两部分。小车静止时活塞刚好位于气缸中间,此时左右两边气体压强均为大气压,假设外界温度不变,已知活塞面积为S,气缸长度为,求:
(1)现小车以一定的加速度向右运动时,发现左侧部分Ⅰ气体的体积正好是静止时的一半,请帮助小明计算出此时小车的加速度a;
(2)当小车以加速度向左匀减速运动时,求右侧部分Ⅱ气体的体积。
参考答案
1.A
【详解】
当气缸转动的角速度为1时,根据向心力方程
当气缸转动的角速度为2时,
根据等温方程
解得1与2的比值为。
故选A。
2.A
【详解】
为了使A管内水银面上升,即使封闭空气的体积减小,根据玻意耳定律可知应使封闭空气的压强增大,所以应缓慢上移B管,使B中水银面比A中水银面高,故A正确。
故选A。
3.B
【详解】
由玻意耳定律得
pV=p1V1
即
20atm×10L=2atm×V1
解得
V1=100L
最多可装的瓶数是
瓶
故选B。
4.D
【详解】
打气时,活塞每推动一次,把体积为V0压强为p0的气体推入容器内,若活塞工作n次,就是把压强为p0体积为nV0的气体压入容器内,容器内原来有压强为p0体积为V的气体,现在全部充入容器中,根据玻意耳定律得
所以
抽气时,每拉动一次,把容器中气体的体积从V膨胀为V+V0,而容器内气体的压强就要减小,活塞推动时将抽气筒中的V0气体排除,而再次拉动活塞时,将容器中剩余的气体从V又膨胀到V+V0容器内的压强继续减小,根据玻意耳定律得,第一次抽气
得
第二次抽气
得
第三次抽气
得
第n次抽气完毕后,气体压强为
故选D。
5.C
【详解】
A.充气过程中壶内气体温度保持不变,分子的平均动能不变,故选项A错误;
B.阀门打开后喷嘴中有雾状酒精喷出是因为瓶内的气体压强大于外界压强,故选项B错误;
C.将阀门打开后壶内气体膨胀,气体从壶中逸出,壶内气体分子数减小,故压强减小,因此选项C正确;
D.从喷壶中喷出的酒精水雾不属于布朗运动,布朗运动人眼看不到,选项D错误。
故选C。
6.A
【详解】
理想气体做等温变化时,由玻意耳定律
可判断出
根据
得到
故
故A正确,BCD错误。
故选A。
7.D
【详解】
根据玻意耳定律得温度一定时,气体的压强与体积成反比,所以体积变为原来的。
故选D。
8.D
【详解】
设容器的容积是V,抽气机的容积是V0,气体发生等温变化,根据玻意耳定律可得
其中
由玻意耳定律可得抽一次时
pV=p1(V+V0)
抽两次时
P1V=p2(V+V0)
……
抽n次时
其中
联立解得
n=5
故选D。
9.D
【详解】
由于无法判断初始时A部分的气体压强和管外大气压强的关系,因此打开阀门一段时间后关闭,气体A的压强可能变大、可能减小也可能不变,所以气体B的体积可能不变、可能减小或增大。
故选D。
10.AD
【详解】
CD.整体分析,由牛顿第二定律有
解得
对水银汞柱分析,由牛顿第二定律有
代入数据解得
根据液体的压强公式有
则
所以C错误;D正确;
AB.静止时,气体的压强为
根据玻意耳定律有
则温度不变时,气体的压强与体积成反比,加速下滑时,气体的压强减小,所以释放后气体体积变大,则A正确;B错误;
故选AD。
11.ABD
【详解】
A.根据玻意耳定律,有
解得
故A正确;
BC.B中气体压强为
所以A中气体压强为大气压强,若外界大气压缓慢增加少许,AB中的气体压强增加,根据玻意耳定律,可知体积减小,l1变小,l2变小。故B正确;C错误;
D.若用手轻按试管,相当于施加一向下的力,AB中的气体压强增加,l1变小,l2变小,B中气体压强
变大,故h2变大。故D正确。
故选ABD。
12.CD
【详解】
A.气体由状态A沿图线1变化到状态B的过程中,压强减小,质量和温度不变,故气体体积增大,所以分子间平均距离增大,A错误;
BC.p-V图像中,图线1在图线2外侧,则图线1对应的温度较高,B错误,C正确;
D.气体由状态A沿图线1变化到状态B的过程中,温度不变,故平均动能不变,所以气体分子的平均速率不变,D正确。
故选CD。
13.BD
【详解】
AB.在实验中,水银柱产生的压强加上封闭空气柱产生的压强等于外界大气压。如果将玻璃管向上提,则管内水银柱上方空气的体积增大,因为温度保持不变,所以压强减小,而此时外界的大气压不变,根据上述等量关系,管内水银柱的压强须增大才能重新平衡,故管内水银柱的高度增大,故A错误,B正确;
CD.将管下插时,体积变小,由pV=C知,压强变大,故内外液面差变小,故C错误,D正确。
故选BD。
14.AD
【详解】
A.图线D→A的斜率不变,由数学知识可知图线的斜率等于pV,斜率不变,则pV不变由气态方程
分析可知温度不变,所以D→A是一个等温过程,故选项A正确;
BC.由图可知A→B过程中,压强变大,体积变大,根据
可知,气体的温度升高,A与B的各状态参量均不相同,故选项BC错误;
D.同理,B→C过程气体的温度不变,而压强减小,根据玻意耳定律
可知体积增大,故选项D正确。
故选AD。
15.AB
【详解】
开始时两活塞处于静止状态,设上、下活塞的面积为S1、S2,气体压强为p,整体由平衡条件可得
解得缸气体压强为
A.给气缸内气体缓慢加热,假设活塞不移动,气体发生等容变化,则温度升高,缸内气体压强增大,由于
故活塞相对气缸向下移动,A正确;
B.大气压变小时,气体压强减小,由玻意耳定律可知气体体积要增大,故活塞要向下移动,B正确;
C.减少几个钢球,整体重力减小,气体压强增大,由玻意耳定律可知气体体积要减小,故活塞要向上移动,C错误;
D.让整个装置自由落体,刚内气体压强等于大气压,原来压强小于大气压,故体积要减小,活塞要向上移动,D错误。
故选AB。
16.(1)5.0×104Pa;(2)
【详解】
(1)根据液体压强关系得
p=p0-ρgh=5.0×104Pa
(2)对管内气体分析初态:p1=p0
V1=SH
末态:p2=p0-ρgh
V2=Sl
由等温变化得
解得
由质量与气体长度成正比关系得
即
带入数据可知
17.(1);(2)8.69cm
【详解】
(1)设刚开始左侧空气柱的压强为,右侧水银柱高出部分的压强为,则
当两边液面相平时设左侧空气柱的压强为,则根据玻意耳定律
即
联立解得
(2)
当两边液面相平时设右侧空气柱的压强为,则
则根据玻意耳定律
解得
18.(1);(2)
【详解】
(1)设玻管的横截面积为,活塞的横截面积为,对玻管中的气体,初态体积和压强分别为
末态体积为
由玻意耳定律有
代入数据解得
(2)设玻管上端恰好与水银面齐平时,活塞到水银面的高度为,对水银面上方的气体,初态体积和压强分别为
,
末态体积和压强分别为
,
由玻意耳定律有
代入数据解得
活塞向下移动的距离为
19.11.5cm
【详解】
初态封闭气体压强
体积
水银上升到细筒中,设粗筒横截面积为s,则
此时封闭气体压强
体积
由玻意耳定律得
解得
活塞B上移的距离
20.(1),方向向右;(2)
【详解】
(1)左右两部分气体温度不变,发生等温变化,根据波意耳定律可知,对左侧气体Ⅰ有
解得
对右侧气体Ⅱ有
解得
对活塞由牛顿第二定律可得
解得此时小车的加速度大小为
方向水平向右。
(2)当小车向左匀减速运动时,活塞所受合力向右,故左侧气体压强较大、体积较小,设活塞偏向左侧距离为x,由波意耳定律对左侧气体Ⅰ得
对右侧气体Ⅱ得
对活塞由牛顿第二定律可得
联立解得
故右侧部分Ⅱ气体的体积为
2.1气体实验定律(Ⅰ)同步作业(解析版)
1.如图所示,在光滑水平面上,一质量为m的导热活塞将一定质量的理想气体封闭在内壁光滑的圆柱形气缸中,开始时活塞和气缸静止,此时气柱长度为l,现使气缸底部绕一竖直轴由静止开始转动,缓慢增大转动的角速度,当气缸转动的角速度为1时,气柱长度为2l,当气缸转动的角速度为2时,气柱长度为3l,若外界大气压不变,则1与2的比值为( )
A.
B.
C.2:3
D.3:2
2.如图所示,竖直放置的粗细相同的玻璃管A、B底部由橡皮软管连接,橡皮管内充满水银。一定质量的空气被水银柱封闭在A管内。B管上方与大气相通。初始时两管水银面向平。A管固定不动,环境温度不变的情况下,为使A管内水银面上升,则应缓慢( )
A.上移B管
B.下移B管
C.右移B管
D.左移B管
3.容积V=10L的钢瓶充满氧后,压强p=20atm,打开钢瓶盖阀门,让氧气分别装到容积为V0=5L的小瓶子中去,若小瓶子已抽成真空,分装到小瓶子中的氧气压强均为p0=2atm。在分装过程中无漏气现象,且温度保持不变,那么最多可装的瓶数是( )
A.2瓶
B.18瓶
C.0.10瓶
D.20瓶
4.只两用活塞气筒的原理如图所示(打气时如图甲,抽气时如图乙),其筒内体积为V0,现将它与另一只容积为V的容器相连接,气筒和容器内的空气压强为p0,已知气筒和容器导热性能良好,当分别作为打气筒和抽气筒时,活塞工作n次后,在上述两种情况下,容器内的气体压强分别为( )
A.,
B.,
C.,
D.,
5.图甲是浇花的一种喷壶,图乙是喷壶的切面图,假设喷壶中装有一部分酒精但未装满,里面有一部分大气压为p0的空气。现将喷壶的盖盖好并密封阀门后,再通过打气筒向喷壶内充入一部分大气压也为p0的气体,并保持阀门关闭,假设此充气过程中壶内气体温度保持不变。研究的气体可视为理想气体,不考虑酒精的蒸发,下列说法正确的是( )
A.壶内充入气体,壶内气体的分子的平均动能增加
B.阀门打开后喷嘴中有雾状酒精喷出是由瓶内酒精分子存在斥力
C.阀门打开后壶内气体的压强不断减小
D.从喷壶中喷出的酒精水雾飘在空中后,水雾的运动为布朗运动
6.不同条件下质量一定的理想气体的密度ρ随压强p变化的下列四种图线中,属等温变化的是( )
A.
B.
C.
D.
7.一定质量的气体在温度保持不变时,压强增大到原来的4倍,则气体的体积变为原来的( )
A.4
B.2
C.
D.
8.现从一体积不变的容器中抽气,假设温度保持不变,每一次抽气后,容器内气体的压强均减小到原来的,要使容器内剩余气体的压强减为原来的,抽气次数应为( )
A.2次
B.3次
C.4次
D.5次
9.如图所示,两端封闭的形管中,初始时连接处有一段水银将气体分为、两部分,现打开阀门一段时间后关闭,期间无水银漏出,则关闭阀门后气体的体积相比初始时( )
A.增大
B.减小
C.不变
D.无法判断
10.有一段12cm长水银柱,在均匀玻璃管中封住一定质量的气体。若将玻璃管管口向上放置在一个倾角为30°的斜面上(如图所示),先用外力使玻璃管静止在斜面上,后由静止释放,玻璃管沿斜面下滑。已知玻璃管与斜面间的动摩擦因数为,大气压强p0相当于76cm汞柱,气体温度不变。则下列说法正确的是( )
A.释放后气体体积变大
B.释放后气体体积变小
C.下滑稳定时密闭气体的压强为80cm汞柱
D.下滑稳定时密闭气体的压强为79cm汞柱
11.如图所示,有一重力可以忽略的薄壁小试管开口向下竖直地浮在很大的水银槽内,试管中有一长为h1的水银柱封住两段气体A、B,A、B气柱长分别为l1、l2,管内外水银面高度差为h2,在保持温度不变的情况下,下列说法正确的是( )
A.开始时h2一定等于h1
B.若外界大气压缓慢增加少许,则h2不变,l1变小,l2变小
C.若外界大气压缓慢增加少许,则h2变小,l1变大,l2变大
D.若用手轻按试管,使试管竖直向下移少许,则h2变大,l1变小,l2变小
12.如图所示,图线1和2分别表示一定质量的气体在不同温度下的等温线。下列说法正确的是( )
A.气体由状态A沿图线1变化到状态B的过程中,分子间平均距离减小
B.图线1对应的温度低于图线2
C.图线1对应的温度高于图线2
D.气体由状态A沿图线1变化到状态B的过程中,气体分子的平均速率不变
13.如图所示,1m左右的玻璃管内,水银柱上面封闭一段气体,管内外水银面的高度差为h=72cm,大气压强为76cmHg,下列说法正确的是( )
A.将管稍微上提,h不变
B.将管稍微上提,h变大
C.将管下插至管顶与管外水银面高度差为70cm时,管内外水银面高度差也是70cm
D.将管下插至管顶与管外水银面高度差为70cm时,管内外水银面高度差小于70cm
14.如图所示,D→A→B→C表示一定质量的某种气体状态变化的一个过程。则下列说法正确的是( )
A.D→A是一个等温过程
B.A→B是一个等温过程
C.A与B的各状态参量均相同
D.B→C体积增大,压强减小,温度不变
15.如图所示的装置,气缸分上、下两部分,下部分的横截面积大于上部分的横截面积,大小活塞分别在上、下气缸内用一根硬杆相连,两活塞可在气缸内一起上下移动。缸内封有一定质量的气体,活塞与缸壁无摩擦且不漏气。初始时,活塞处于静止态,小活塞上的杯子里放有大量钢球。在列哪些情况下,两活塞将相对气缸向下移动( )
A.给气缸内气体援慢加热
B.大气压变小
C.减少几个钢球
D.让整个装置自由落体
16.在如图所示的机械式取水装置中,活塞从阀门处开始往上移动时,阀门开启,活塞向下移动时,阀门关闭,空气从活塞处溢出,地下水就通过直管被抽上来,地下水位线距离阀门的高度H=40m,用力向上拉活塞到某位置,使直管中水缓慢上升h=5m,然后活塞关闭。已知水的密度ρ=1.0×103kg/m3,外界大气压强p0=1.0×105Pa,重力加速度g=10m/s?,直管中的气体可视为理想气体,抽水过程直管中的空气温度不变。求:
(1)直管中水上升后管内气体压强p的大小;
(2)阀门关闭后,求阀门下方直管中剩余空气质量△m与直管中原空气质量m0的比值。
17.如图所示,粗细均匀的等高U形玻璃管竖直放置,左管封闭,右端开口,用水银柱封闭长为的一段空气柱,右侧水银柱比左侧高出,已知大气压为。现用一质量不计的薄活塞封住右端开口,缓慢向下压活塞使两边液面相平,此过程中环境温度始终不变,当两边液面相平时,求:
(1)左侧空气柱的压强。
(2)右侧空气柱的长度多少厘米?(计算结果保留两位小数)
18.如图,开口向上的气缸内盛有一定深度的水银,一粗细均匀,长为l=24cm且下端开口的细玻管竖直漂浮在水银中。平衡时,玻管露出水银面的高度和进入玻管中的水银柱长度均为h1=6cm,轻质活塞到水银面的高度为h0=12cm,水银面上方的气体压强为p0=76
cm
Hg。现施外力使活塞缓慢向下移动,当玻管上端恰好与水银面齐平时,进入玻管中的水银柱长度为h2=12cm。活塞与气缸壁间的摩擦不计且密封性良好,玻管的横截面积远小于气缸的横截面积,整个过程中各部分气体的温度保持不变,求:
(1)玻管上端恰好与水银面齐平时,玻管内气体的压强;
(2)整个过程中活塞向下移动的距离。
19.如图所示,竖直圆简是固定不动的,粗筒横截面积是细筒的2倍,细筒足够长粗筒中A、B两轻质活塞间封有一定质量的空气(可视为理想气体),气柱长。活塞A上方的水银深,两活塞的重力及与筒壁间的摩擦不计,用外力向上托住活塞B使之处于平衡状态,水银面与粗筒上端相平现使活塞B缓慢上移,直至水银的三分之二被推入细筒中,求活塞B上移的距离。(设在整个过程中气柱的温度不变,大气压强当于的水银柱产生的压强)
20.如图所示是小明学习完热学内容后设计的一个测量小车加速度的简易装置。在车上水平固定内壁光滑且导热的气缸,缸内有一定质量的空气(可视为理想气体〕,被质量为m且厚度不计的活塞分隔成Ⅰ、Ⅱ两部分。小车静止时活塞刚好位于气缸中间,此时左右两边气体压强均为大气压,假设外界温度不变,已知活塞面积为S,气缸长度为,求:
(1)现小车以一定的加速度向右运动时,发现左侧部分Ⅰ气体的体积正好是静止时的一半,请帮助小明计算出此时小车的加速度a;
(2)当小车以加速度向左匀减速运动时,求右侧部分Ⅱ气体的体积。
参考答案
1.A
【详解】
当气缸转动的角速度为1时,根据向心力方程
当气缸转动的角速度为2时,
根据等温方程
解得1与2的比值为。
故选A。
2.A
【详解】
为了使A管内水银面上升,即使封闭空气的体积减小,根据玻意耳定律可知应使封闭空气的压强增大,所以应缓慢上移B管,使B中水银面比A中水银面高,故A正确。
故选A。
3.B
【详解】
由玻意耳定律得
pV=p1V1
即
20atm×10L=2atm×V1
解得
V1=100L
最多可装的瓶数是
瓶
故选B。
4.D
【详解】
打气时,活塞每推动一次,把体积为V0压强为p0的气体推入容器内,若活塞工作n次,就是把压强为p0体积为nV0的气体压入容器内,容器内原来有压强为p0体积为V的气体,现在全部充入容器中,根据玻意耳定律得
所以
抽气时,每拉动一次,把容器中气体的体积从V膨胀为V+V0,而容器内气体的压强就要减小,活塞推动时将抽气筒中的V0气体排除,而再次拉动活塞时,将容器中剩余的气体从V又膨胀到V+V0容器内的压强继续减小,根据玻意耳定律得,第一次抽气
得
第二次抽气
得
第三次抽气
得
第n次抽气完毕后,气体压强为
故选D。
5.C
【详解】
A.充气过程中壶内气体温度保持不变,分子的平均动能不变,故选项A错误;
B.阀门打开后喷嘴中有雾状酒精喷出是因为瓶内的气体压强大于外界压强,故选项B错误;
C.将阀门打开后壶内气体膨胀,气体从壶中逸出,壶内气体分子数减小,故压强减小,因此选项C正确;
D.从喷壶中喷出的酒精水雾不属于布朗运动,布朗运动人眼看不到,选项D错误。
故选C。
6.A
【详解】
理想气体做等温变化时,由玻意耳定律
可判断出
根据
得到
故
故A正确,BCD错误。
故选A。
7.D
【详解】
根据玻意耳定律得温度一定时,气体的压强与体积成反比,所以体积变为原来的。
故选D。
8.D
【详解】
设容器的容积是V,抽气机的容积是V0,气体发生等温变化,根据玻意耳定律可得
其中
由玻意耳定律可得抽一次时
pV=p1(V+V0)
抽两次时
P1V=p2(V+V0)
……
抽n次时
其中
联立解得
n=5
故选D。
9.D
【详解】
由于无法判断初始时A部分的气体压强和管外大气压强的关系,因此打开阀门一段时间后关闭,气体A的压强可能变大、可能减小也可能不变,所以气体B的体积可能不变、可能减小或增大。
故选D。
10.AD
【详解】
CD.整体分析,由牛顿第二定律有
解得
对水银汞柱分析,由牛顿第二定律有
代入数据解得
根据液体的压强公式有
则
所以C错误;D正确;
AB.静止时,气体的压强为
根据玻意耳定律有
则温度不变时,气体的压强与体积成反比,加速下滑时,气体的压强减小,所以释放后气体体积变大,则A正确;B错误;
故选AD。
11.ABD
【详解】
A.根据玻意耳定律,有
解得
故A正确;
BC.B中气体压强为
所以A中气体压强为大气压强,若外界大气压缓慢增加少许,AB中的气体压强增加,根据玻意耳定律,可知体积减小,l1变小,l2变小。故B正确;C错误;
D.若用手轻按试管,相当于施加一向下的力,AB中的气体压强增加,l1变小,l2变小,B中气体压强
变大,故h2变大。故D正确。
故选ABD。
12.CD
【详解】
A.气体由状态A沿图线1变化到状态B的过程中,压强减小,质量和温度不变,故气体体积增大,所以分子间平均距离增大,A错误;
BC.p-V图像中,图线1在图线2外侧,则图线1对应的温度较高,B错误,C正确;
D.气体由状态A沿图线1变化到状态B的过程中,温度不变,故平均动能不变,所以气体分子的平均速率不变,D正确。
故选CD。
13.BD
【详解】
AB.在实验中,水银柱产生的压强加上封闭空气柱产生的压强等于外界大气压。如果将玻璃管向上提,则管内水银柱上方空气的体积增大,因为温度保持不变,所以压强减小,而此时外界的大气压不变,根据上述等量关系,管内水银柱的压强须增大才能重新平衡,故管内水银柱的高度增大,故A错误,B正确;
CD.将管下插时,体积变小,由pV=C知,压强变大,故内外液面差变小,故C错误,D正确。
故选BD。
14.AD
【详解】
A.图线D→A的斜率不变,由数学知识可知图线的斜率等于pV,斜率不变,则pV不变由气态方程
分析可知温度不变,所以D→A是一个等温过程,故选项A正确;
BC.由图可知A→B过程中,压强变大,体积变大,根据
可知,气体的温度升高,A与B的各状态参量均不相同,故选项BC错误;
D.同理,B→C过程气体的温度不变,而压强减小,根据玻意耳定律
可知体积增大,故选项D正确。
故选AD。
15.AB
【详解】
开始时两活塞处于静止状态,设上、下活塞的面积为S1、S2,气体压强为p,整体由平衡条件可得
解得缸气体压强为
A.给气缸内气体缓慢加热,假设活塞不移动,气体发生等容变化,则温度升高,缸内气体压强增大,由于
故活塞相对气缸向下移动,A正确;
B.大气压变小时,气体压强减小,由玻意耳定律可知气体体积要增大,故活塞要向下移动,B正确;
C.减少几个钢球,整体重力减小,气体压强增大,由玻意耳定律可知气体体积要减小,故活塞要向上移动,C错误;
D.让整个装置自由落体,刚内气体压强等于大气压,原来压强小于大气压,故体积要减小,活塞要向上移动,D错误。
故选AB。
16.(1)5.0×104Pa;(2)
【详解】
(1)根据液体压强关系得
p=p0-ρgh=5.0×104Pa
(2)对管内气体分析初态:p1=p0
V1=SH
末态:p2=p0-ρgh
V2=Sl
由等温变化得
解得
由质量与气体长度成正比关系得
即
带入数据可知
17.(1);(2)8.69cm
【详解】
(1)设刚开始左侧空气柱的压强为,右侧水银柱高出部分的压强为,则
当两边液面相平时设左侧空气柱的压强为,则根据玻意耳定律
即
联立解得
(2)
当两边液面相平时设右侧空气柱的压强为,则
则根据玻意耳定律
解得
18.(1);(2)
【详解】
(1)设玻管的横截面积为,活塞的横截面积为,对玻管中的气体,初态体积和压强分别为
末态体积为
由玻意耳定律有
代入数据解得
(2)设玻管上端恰好与水银面齐平时,活塞到水银面的高度为,对水银面上方的气体,初态体积和压强分别为
,
末态体积和压强分别为
,
由玻意耳定律有
代入数据解得
活塞向下移动的距离为
19.11.5cm
【详解】
初态封闭气体压强
体积
水银上升到细筒中,设粗筒横截面积为s,则
此时封闭气体压强
体积
由玻意耳定律得
解得
活塞B上移的距离
20.(1),方向向右;(2)
【详解】
(1)左右两部分气体温度不变,发生等温变化,根据波意耳定律可知,对左侧气体Ⅰ有
解得
对右侧气体Ⅱ有
解得
对活塞由牛顿第二定律可得
解得此时小车的加速度大小为
方向水平向右。
(2)当小车向左匀减速运动时,活塞所受合力向右,故左侧气体压强较大、体积较小,设活塞偏向左侧距离为x,由波意耳定律对左侧气体Ⅰ得
对右侧气体Ⅱ得
对活塞由牛顿第二定律可得
联立解得
故右侧部分Ⅱ气体的体积为
同课章节目录
- 第一章 分子动理论
- 第一节 物质是由大量分子组成的
- 第二节 分子热运动与分子力
- 第三节 气体分子运动的统计规律
- 第二章 气体、液体和固态
- 第一节 气体实验定律(Ⅰ)
- 第二节 气体实验定律(Ⅱ)
- 第三节 气体实验定律的微观解释
- 第四节 液体的表面张力
- 第五节 晶体
- 第六节 新材料
- 第三章 热力学定律
- 第一节 热力学第一定律
- 第二节 能量守恒定律及其应用
- 第三节 热力学第二定律
- 第四章 波粒二象性
- 第一节 光电效应
- 第二节 光电效应方程及其意义
- 第三节 光的波粒二象性
- 第四节 德布罗意波
- 第五节 不确定性关系
- 第五章 原子与原子核
- 第一节 原子的结构
- 第二节 放射性元素的衰变
- 第三节 核力与核反应方程
- 第四节 放射性同位素
- 第五节 裂变和聚变
