湘教版数学八年级上册期末测试卷及答案(word版含答案)
文档属性
| 名称 | 湘教版数学八年级上册期末测试卷及答案(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 247.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-23 19:51:46 | ||
图片预览


文档简介
湘教版数学八年级上册期末测试卷
(时间:120分
分值:120分)
一、选择题(每小题3分,共10小题,满分30分)
1.(3分)一个等腰三角形的两个内角和为100°,则它的顶角度数为(
)
A.50°
B.80°
C.50°或80°
D.20°或80°
2.(3分)已知△ABC的六个元素,下面甲、乙、丙三个三角形中标出了某些元素,则与△ABC全等的三角形是(
)
A.只有乙
B.只有丙
C.甲和乙
D.乙和丙
3.(3分)下列运算正确的是(
)
A.2﹣3=﹣6
B.(﹣2)3=﹣6
C.()﹣2=
D.2﹣3=
4.(3分)已知一粒大米的质量约为0.000021千克,这个数用科学记数法表示为(
)
A.0.21×10﹣4
B.2.1×10﹣4
C.2.1×10﹣5
D.21×10﹣6
5.(3分)若3x=4,9y=7,则3x﹣2y=(
)
A.
B.
C.
D.
6.(3分)下列代数式①,②,③,④中,分式有(
)
A.1个
B.2个
C.3个
D.4个
7.(3分)根据分式的基本性质填空:=,括号内应填(
)
A.x2﹣3x
B.x3﹣3
C.x2﹣3
D.x4﹣3x
8.(3分)下列计算正确的是(
)
A.30=0
B.3﹣2=﹣6
C.3﹣2=﹣
D.3﹣2=
9.(3分)若代数式有意义,则x必须满足条件(
)
A.x≥﹣1
B.x≠﹣1
C.x≥1
D.x≤﹣1
10.(3分)已知一个等腰三角形的两边长分别是5cm与6cm,则这个等腰三角形的周长为(
)
A.16cm
B.17cm
C.16cm或17cm
D.无法确定
二、填空题(每小题3分,共8小题,满分24分)
11.(3分)当x=时,分式无意义.
12.(3分)计算:2x2y3÷xy2=.
13.(3分)如图,△ABC≌△BAD,A与B,C与D是对应点,若AB=4cm,BD=4.5cm,AD=1.5cm,则BC=cm.
14.(3分)如图,在△ABC中,AB=AD=DC,∠BAD=20°,则∠C=.
15.(3分)如图,已知AD=BC,则再添加一个条件(只填一种),可证出△ABC≌△BAD.
16.(3分)计算:()2015()2016=.
17.(3分)巳知等腰三角形一底角为30°,则这个等腰三角形顶角的大小是度.
18.(3分)如图,已知在△ABC中,BC=10cm,AB的垂直平分线EF交BC与点F,AC的垂直平分线MN交BC于点N,则△AFN的周长为cm.
三、解答题(19题每小题8分,20题6分,满分14分)
19.(8分)①化简:
②计算:.
20.(6分)求当x取何值时,代数式﹣的值不小于1?
四、分析与说理(每小题8分,共2小题,满分16分)
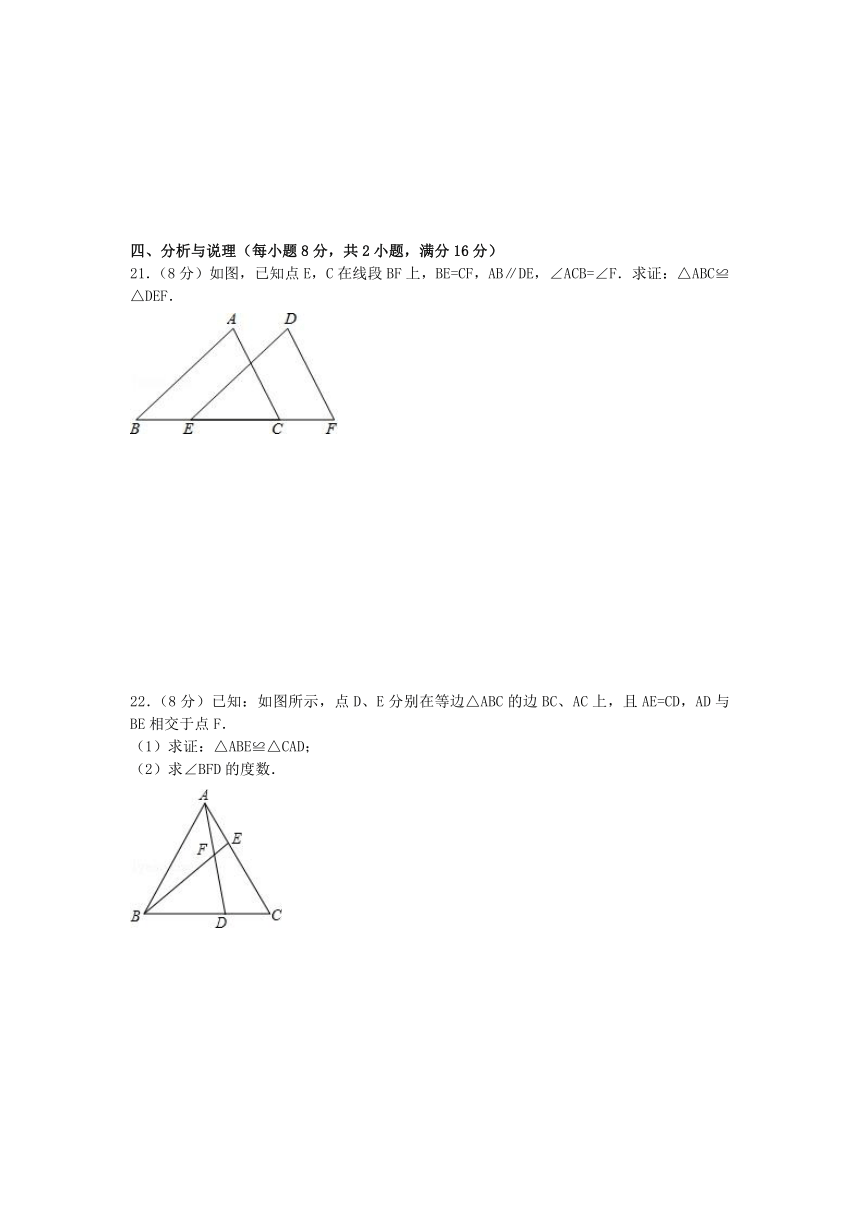
21.(8分)如图,已知点E,C在线段BF上,BE=CF,AB∥DE,∠ACB=∠F.求证:△ABC≌△DEF.
22.(8分)已知:如图所示,点D、E分别在等边△ABC的边BC、AC上,且AE=CD,AD与BE相交于点F.
(1)求证:△ABE≌△CAD;
(2)求∠BFD的度数.
五、实践与应用(每小题8分,共2小题,满分16分)
23.(8分)娄底到长沙的距离约为120km,小刘开着小轿车,小张开着大货车,都从娄底去长沙,小刘比小张晚出发15分钟,最后两车同时到达长沙,已知小轿车的速度是大货车速度的1.2倍,求小轿车和大货车的速度各是多少?(列方程解答)
24.(8分)某校组织开展了“娄底是我家,建设娄底靠大家”的环保知识竞赛,共25道竞赛题,选对一题得4分,不选或选错每题扣2分,大赛组委会规定总得分不低于80分获奖,那么至少应选对多少道题才能获奖?(列不等式解答)
六、阅读与探究(每小题10分,共2小题,满分20分)
25.(10分)阅读下列材料,并解决问题:
①已知方程x2+3x+2=0的两根分别为x1=﹣1,x2=﹣2,计算:x1+x2=,x1?x2=
②已知方程x2﹣3x﹣4=0的两根分别为x1=4,x2=﹣1,计算:x1+x2=,x1?x2=
③已知关于x的方程x2+px+q=0有两根分别记作x1,x2,且x1=,x2=,请通过计算x1+x2及x1?x2,探究出它们与p、q的关系.
26.(10分)在长方形ABCD中,AD=2AB,E是AD的中点,一块三角板的直角顶点与点E重合,将三角板绕点E按顺时针方向旋转,当三角板的两直角边分别与AB、BC分别相交于点M,N时,观察或测量BM与CN的长度,你能得到什么结论?并证明你的结论.
参考答案:
一、选择题。
1.D.
2.D.
3.D.
4.C.
5.B.
6.B.
7.C.
8.D.
9.A.
10.C.
二、填空题。
11.﹣3.
12.2xy.
13.1.5.
14.40°.
15.AC=BD.
16.2﹣.
17.120.
18.10.
三、解答题。
19.解:①原式=+
=
=;
②原式=2++﹣3
=2﹣.
20.解:根据题意得:﹣≥1,
3(3x﹣5)﹣7(x+4)≥21,
9x﹣15﹣7x﹣28≥21,
9x﹣7x≥21+28+15,
2x≥64,
x≥32.
故当x≥32时,代数式﹣的值不小于1.
四、分析与说理。
21.证明:∵AB∥DE,
∴∠B=∠DEF.
∵BE=CF,
∴BC=EF.
∵∠ACB=∠F,
∴,
∴△ABC≌△DEF(ASA).
22.
解:(1)∵△ABC为等边三角形,
∴AB=AC,AE=CD,∠BAE=∠C=60°,
在△ABE和△ACD中,
,
∴△ABE≌△CAD(SAS),
∴AD=BE.
(2)∵△ABE≌△CAD,
∴∠ABE=∠CAD,
∴∠BFD=∠ABE+∠BAD=∠CAD+∠BAD=∠BAC=60°.
五、实践与应用。
23.解:设大货车的速度为xkm/时,由题意得:
﹣=,
解得:x=80,
经检验:x=80是分式方程的解,
1.2x=1.2×80=96,
答:大货车的速度为80km/时,小轿车的速度为96km/时.
24.解:设做对x道.根据题意列出不等式:
4x﹣2×(25﹣x)≥80,
解得:x≥,
∵=21,
∴x最小取22.
答:至少应选对22道题才能获奖.
六、阅读与探究。
25.解:①∵x1=﹣1,x2=﹣2,
∴x1+x2=﹣3,x1?x2=2;
②∵x1=4,x2=﹣1,
∴x1+x2=3,x1?x2=﹣4;
③∵x1=,x2=,
∴x1+x2=+=﹣p,
x1x2=?=q,
即x1+x2=﹣p,x1x2=q.
故答案为:﹣3,2;3,﹣4.
26.
解:BM与与CN的长度相等.
证明:在矩形ABCD中,AD=2AB,E是AD的中点,
如图,作EF⊥BC于点F,则有AB=AE=EF=FC,
∵∠AEM+∠DEN=90°,∠FEN+∠DEN=90°,
∴∠AEM=∠FEN,
在Rt△AME和Rt△FNE中,
,
∴Rt△AME≌Rt△FNE,
∴AM=FN,
∴MB=CN.
(时间:120分
分值:120分)
一、选择题(每小题3分,共10小题,满分30分)
1.(3分)一个等腰三角形的两个内角和为100°,则它的顶角度数为(
)
A.50°
B.80°
C.50°或80°
D.20°或80°
2.(3分)已知△ABC的六个元素,下面甲、乙、丙三个三角形中标出了某些元素,则与△ABC全等的三角形是(
)
A.只有乙
B.只有丙
C.甲和乙
D.乙和丙
3.(3分)下列运算正确的是(
)
A.2﹣3=﹣6
B.(﹣2)3=﹣6
C.()﹣2=
D.2﹣3=
4.(3分)已知一粒大米的质量约为0.000021千克,这个数用科学记数法表示为(
)
A.0.21×10﹣4
B.2.1×10﹣4
C.2.1×10﹣5
D.21×10﹣6
5.(3分)若3x=4,9y=7,则3x﹣2y=(
)
A.
B.
C.
D.
6.(3分)下列代数式①,②,③,④中,分式有(
)
A.1个
B.2个
C.3个
D.4个
7.(3分)根据分式的基本性质填空:=,括号内应填(
)
A.x2﹣3x
B.x3﹣3
C.x2﹣3
D.x4﹣3x
8.(3分)下列计算正确的是(
)
A.30=0
B.3﹣2=﹣6
C.3﹣2=﹣
D.3﹣2=
9.(3分)若代数式有意义,则x必须满足条件(
)
A.x≥﹣1
B.x≠﹣1
C.x≥1
D.x≤﹣1
10.(3分)已知一个等腰三角形的两边长分别是5cm与6cm,则这个等腰三角形的周长为(
)
A.16cm
B.17cm
C.16cm或17cm
D.无法确定
二、填空题(每小题3分,共8小题,满分24分)
11.(3分)当x=时,分式无意义.
12.(3分)计算:2x2y3÷xy2=.
13.(3分)如图,△ABC≌△BAD,A与B,C与D是对应点,若AB=4cm,BD=4.5cm,AD=1.5cm,则BC=cm.
14.(3分)如图,在△ABC中,AB=AD=DC,∠BAD=20°,则∠C=.
15.(3分)如图,已知AD=BC,则再添加一个条件(只填一种),可证出△ABC≌△BAD.
16.(3分)计算:()2015()2016=.
17.(3分)巳知等腰三角形一底角为30°,则这个等腰三角形顶角的大小是度.
18.(3分)如图,已知在△ABC中,BC=10cm,AB的垂直平分线EF交BC与点F,AC的垂直平分线MN交BC于点N,则△AFN的周长为cm.
三、解答题(19题每小题8分,20题6分,满分14分)
19.(8分)①化简:
②计算:.
20.(6分)求当x取何值时,代数式﹣的值不小于1?
四、分析与说理(每小题8分,共2小题,满分16分)
21.(8分)如图,已知点E,C在线段BF上,BE=CF,AB∥DE,∠ACB=∠F.求证:△ABC≌△DEF.
22.(8分)已知:如图所示,点D、E分别在等边△ABC的边BC、AC上,且AE=CD,AD与BE相交于点F.
(1)求证:△ABE≌△CAD;
(2)求∠BFD的度数.
五、实践与应用(每小题8分,共2小题,满分16分)
23.(8分)娄底到长沙的距离约为120km,小刘开着小轿车,小张开着大货车,都从娄底去长沙,小刘比小张晚出发15分钟,最后两车同时到达长沙,已知小轿车的速度是大货车速度的1.2倍,求小轿车和大货车的速度各是多少?(列方程解答)
24.(8分)某校组织开展了“娄底是我家,建设娄底靠大家”的环保知识竞赛,共25道竞赛题,选对一题得4分,不选或选错每题扣2分,大赛组委会规定总得分不低于80分获奖,那么至少应选对多少道题才能获奖?(列不等式解答)
六、阅读与探究(每小题10分,共2小题,满分20分)
25.(10分)阅读下列材料,并解决问题:
①已知方程x2+3x+2=0的两根分别为x1=﹣1,x2=﹣2,计算:x1+x2=,x1?x2=
②已知方程x2﹣3x﹣4=0的两根分别为x1=4,x2=﹣1,计算:x1+x2=,x1?x2=
③已知关于x的方程x2+px+q=0有两根分别记作x1,x2,且x1=,x2=,请通过计算x1+x2及x1?x2,探究出它们与p、q的关系.
26.(10分)在长方形ABCD中,AD=2AB,E是AD的中点,一块三角板的直角顶点与点E重合,将三角板绕点E按顺时针方向旋转,当三角板的两直角边分别与AB、BC分别相交于点M,N时,观察或测量BM与CN的长度,你能得到什么结论?并证明你的结论.
参考答案:
一、选择题。
1.D.
2.D.
3.D.
4.C.
5.B.
6.B.
7.C.
8.D.
9.A.
10.C.
二、填空题。
11.﹣3.
12.2xy.
13.1.5.
14.40°.
15.AC=BD.
16.2﹣.
17.120.
18.10.
三、解答题。
19.解:①原式=+
=
=;
②原式=2++﹣3
=2﹣.
20.解:根据题意得:﹣≥1,
3(3x﹣5)﹣7(x+4)≥21,
9x﹣15﹣7x﹣28≥21,
9x﹣7x≥21+28+15,
2x≥64,
x≥32.
故当x≥32时,代数式﹣的值不小于1.
四、分析与说理。
21.证明:∵AB∥DE,
∴∠B=∠DEF.
∵BE=CF,
∴BC=EF.
∵∠ACB=∠F,
∴,
∴△ABC≌△DEF(ASA).
22.
解:(1)∵△ABC为等边三角形,
∴AB=AC,AE=CD,∠BAE=∠C=60°,
在△ABE和△ACD中,
,
∴△ABE≌△CAD(SAS),
∴AD=BE.
(2)∵△ABE≌△CAD,
∴∠ABE=∠CAD,
∴∠BFD=∠ABE+∠BAD=∠CAD+∠BAD=∠BAC=60°.
五、实践与应用。
23.解:设大货车的速度为xkm/时,由题意得:
﹣=,
解得:x=80,
经检验:x=80是分式方程的解,
1.2x=1.2×80=96,
答:大货车的速度为80km/时,小轿车的速度为96km/时.
24.解:设做对x道.根据题意列出不等式:
4x﹣2×(25﹣x)≥80,
解得:x≥,
∵=21,
∴x最小取22.
答:至少应选对22道题才能获奖.
六、阅读与探究。
25.解:①∵x1=﹣1,x2=﹣2,
∴x1+x2=﹣3,x1?x2=2;
②∵x1=4,x2=﹣1,
∴x1+x2=3,x1?x2=﹣4;
③∵x1=,x2=,
∴x1+x2=+=﹣p,
x1x2=?=q,
即x1+x2=﹣p,x1x2=q.
故答案为:﹣3,2;3,﹣4.
26.
解:BM与与CN的长度相等.
证明:在矩形ABCD中,AD=2AB,E是AD的中点,
如图,作EF⊥BC于点F,则有AB=AE=EF=FC,
∵∠AEM+∠DEN=90°,∠FEN+∠DEN=90°,
∴∠AEM=∠FEN,
在Rt△AME和Rt△FNE中,
,
∴Rt△AME≌Rt△FNE,
∴AM=FN,
∴MB=CN.
同课章节目录
