24.4弧长和扇形面积(第1课时) 课件(共34张PPT)
文档属性
| 名称 | 24.4弧长和扇形面积(第1课时) 课件(共34张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-09-11 14:47:00 | ||
图片预览




文档简介
(共34张PPT)
24.4
弧长和扇形面积
---第1课时
人教版
九年级上
教学目标
1.掌握弧长和扇形面积公式的探求过程.(难点)
2.会利用弧长和扇形面积的计算公式进行计算.(重点)
情境导入
问题1
如图,在运动会的4×100米比赛中,为什么每个运动员他们的起跑线不在同一处?
问题2
怎样来计算弯道的“展直长度”?
因为要保证这些弯道的“展直长度”是一样的.
合作探究
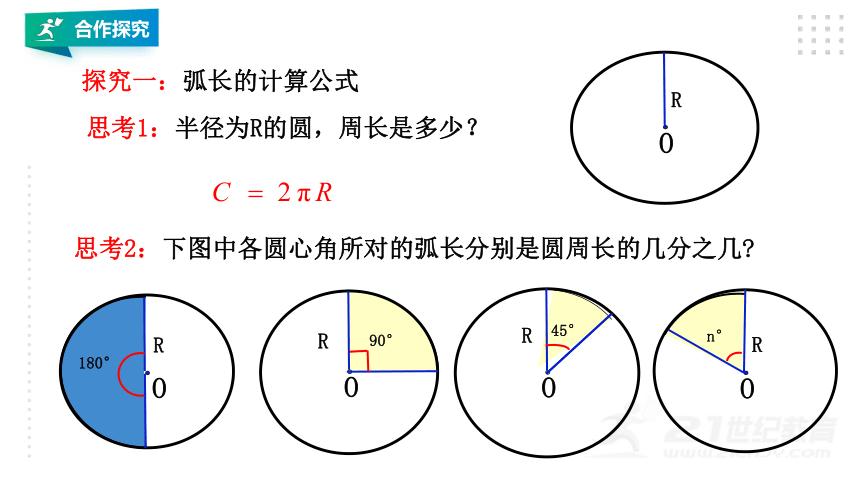
思考1:半径为R的圆,周长是多少?
O
R
思考2:下图中各圆心角所对的弧长分别是圆周长的几分之几?
O
R
180°
O
R
90°
O
R
45°
O
R
n°
探究一:弧长的计算公式
合作探究
(1)
圆心角是180°,占整个周角的
,因此它所对的弧长是圆周长的______.
(2)
圆心角是90°,占整个周角的
,因此它所对的弧长是圆周长的______.
(3)
圆心角是45°,占整个周角的
,因此它所对的弧长是圆周长的_______.
(4)
圆心角是n°,占整个周角的
,因此它所对的弧长是圆周长的_______.
合作探究
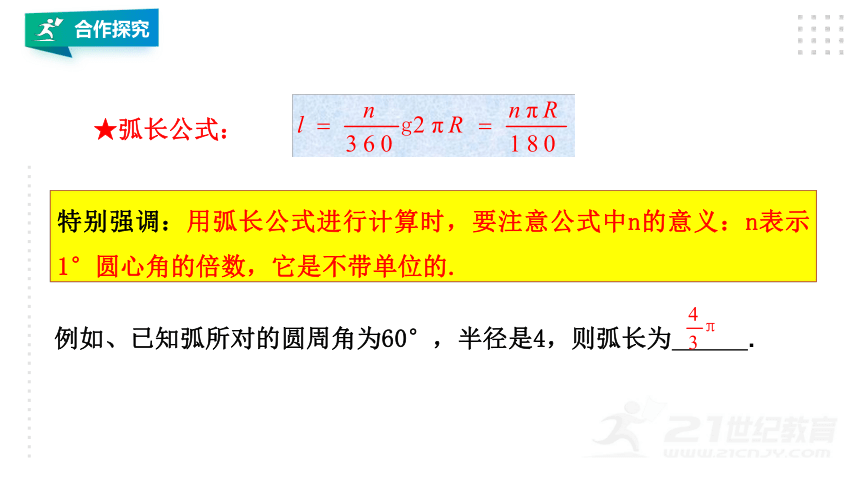
特别强调:用弧长公式进行计算时,要注意公式中n的意义:n表示1°圆心角的倍数,它是不带单位的.
★弧长公式:
例如、已知弧所对的圆周角为60°,半径是4,则弧长为
.
合作探究
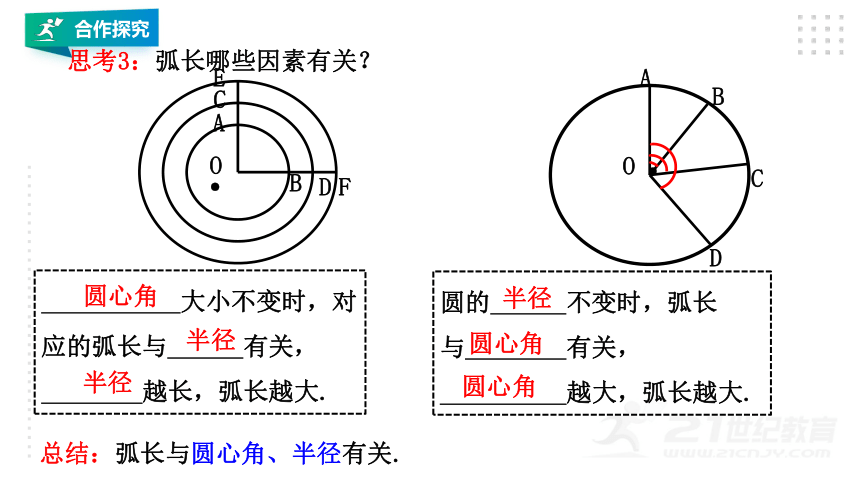
大小不变时,对应的弧长与
有关,
越长,弧长越大.
圆心角
半径
半径
圆的
不变时,弧长
与
有关,
越大,弧长越大.
圆心角
半径
圆心角
总结:弧长与圆心角、半径有关.
O
●
A
B
D
C
E
F
O
●
A
B
C
D
思考3:弧长哪些因素有关?
典例精析
例1
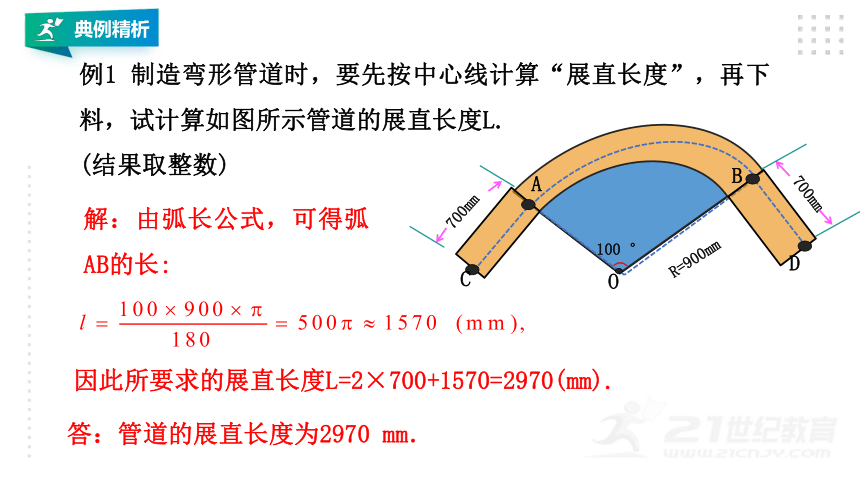
制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算如图所示管道的展直长度L.
(结果取整数)
解:由弧长公式,可得弧AB的长:
因此所要求的展直长度L=2×700+1570=2970(mm).
答:管道的展直长度为2970
mm.
700mm
700mm
R=900mm
(
100
°
A
C
B
D
O
趁热打铁
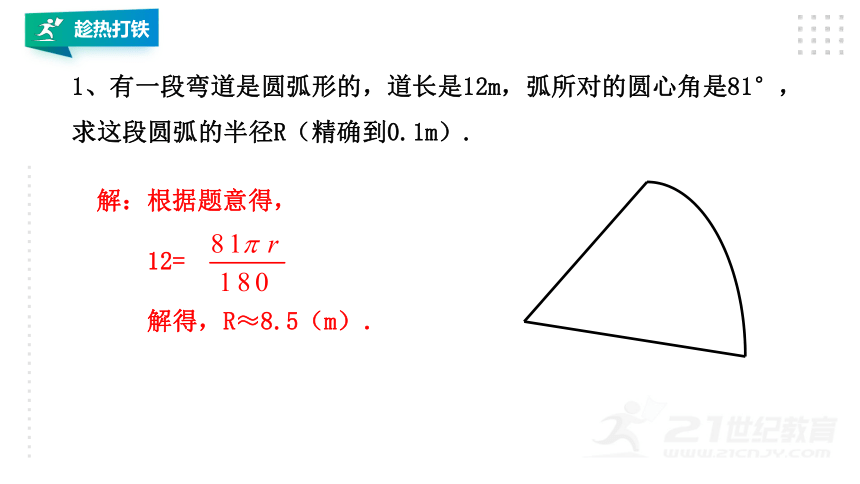
1、有一段弯道是圆弧形的,道长是12m,弧所对的圆心角是81°,求这段圆弧的半径R(精确到0.1m).
解:根据题意得,
12=
解得,R≈8.5(m).
合作探究
探究二:扇形面积的计算公式
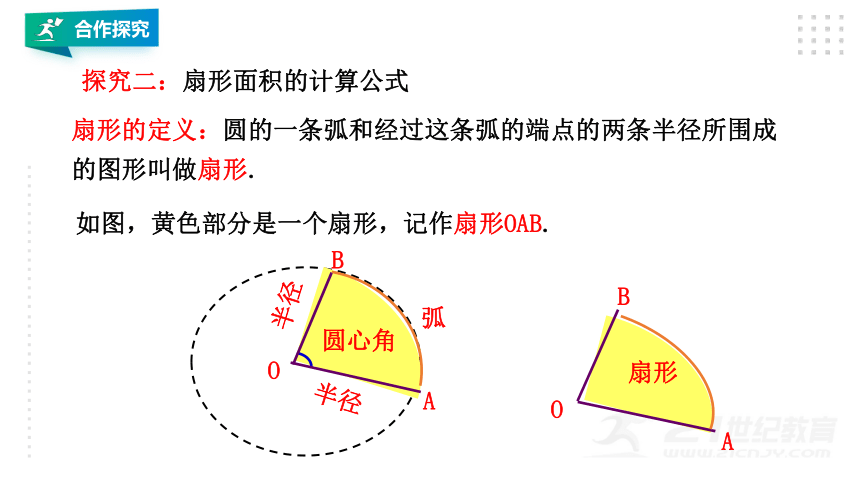
扇形的定义:圆的一条弧和经过这条弧的端点的两条半径所围成的图形叫做扇形.
半径
半径
O
B
A
圆心角
弧
O
B
A
扇形
如图,黄色部分是一个扇形,记作扇形OAB.
趁热打铁
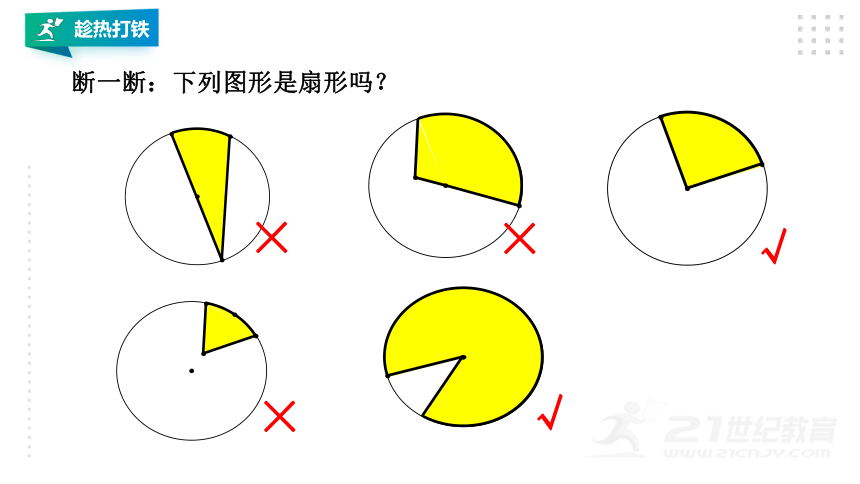
断一断:下列图形是扇形吗?
√
×
×
×
√
合作探究
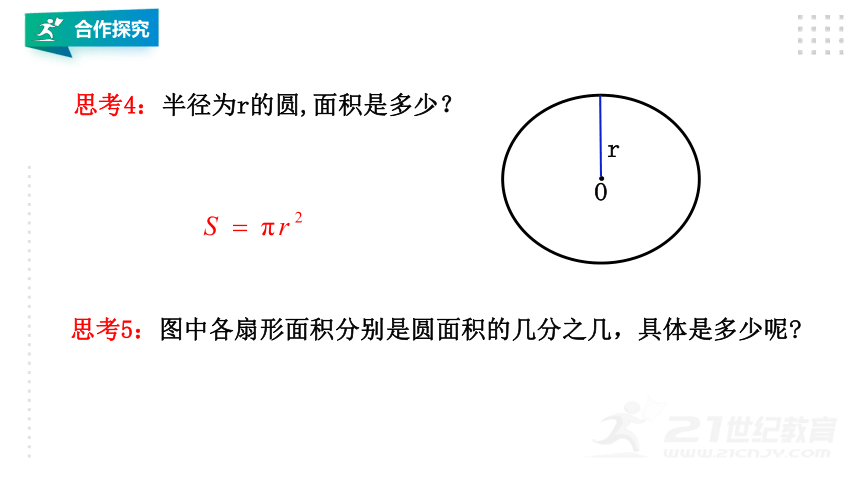
思考4:半径为r的圆,面积是多少?
O
r
思考5:图中各扇形面积分别是圆面积的几分之几,具体是多少呢?
合作探究
O
R
180°
O
R
90°
O
R
45°
O
R
n°
圆心角占
周角的比例
扇形面积占
圆面积的比例
扇形的
面积
=
=
=
=
合作探究
★扇形面积公式:
半径为r的圆中,圆心角为n°的扇形的面积
特别强调:
①公式中n的意义:n表示1°圆心角的倍数,
它是不带单位的;
②公式要理解记忆(即按照上面推导过程记忆).
合作探究
大小不变时,对应的扇形面积与
有关,
越长,面积越大.
圆心角
半径
半径
圆的
不变时,扇形面积
与
有关,
越大,面积越大.
圆心角
半径
圆心角
总结:扇形的面积与圆心角、半径有关.
O
●
A
B
D
C
E
F
O
●
A
B
C
D
思考6:扇形的面积与哪些因素有关?
合作探究
思考7:扇形的面积公式与弧长公式有联系吗?
A
B
O
O
趁热打铁
2.已知半径为2
cm的扇形,其弧长为
cm,则这个扇形的面积
S扇形=
.
1.已知扇形的圆心角为150°,半径为3,则这个扇形的面积
S扇形=
.
典例精析
例3
如图,水平放置的圆柱形排水管道的截面半径是0.6
m,其中水面高0.3
m,求截面上有水部分的面积.(结果保留小数点后两位)
(1)
O
.
B
A
C
思考1:截面上有水部分的面积是指图上哪一部分?
解:阴影部分.
典例精析
O.
B
A
C
D
(2)
O.
B
A
C
D
(3)
思考2:水面高0.3
m是指哪一条线段的长?这条线段应该怎样画出来?
水面高0.3
m是指线段DC的长.
作法:过点O作OD⊥AB于D,并延长OD交圆O于C.
思考3:要求图中阴影部分的面积,应该怎么办?
S阴影=S扇形OAB-
S△OAB
典例精析
∵
OC=0.6
m,
DC=0.3
m,
∴
OD=OC-
DC=0.3
m.
∴
OD=DC.
又
AD
⊥DC,
∴AD是线段OC的垂直平分线.
∴AC=AO=OC.
∴
∠AOD=60?,∠AOB=120?.
O.
B
A
C
D
解:如图,连接OA,OB,过点O作弦AB的垂线,垂足为D,交
于点C,连接AC.
典例精析
有水部分的面积:
S=S扇形OAB
-
SΔOAB
在Rt△AOD中,OA=0.6
m,OD=0.3
m,
∴AD=
m.∴AB=2AD=
m.
O.
B
A
C
D
趁热打铁
1、如图、水平放置的圆柱形排水管道的截面半径是0.6
m,其中水面高0.9
m,求截面上有水部分的面积.
O
A
B
D
C
E
解:
S=S扇形OAB
+
SΔOAB
合作探究
O
O
弓形的面积=扇形的面积±三角形的面积
S弓形=S扇形-S三角形
S弓形=S扇形+S三角形
★弓形的面积公式:
综合演练
1.某扇形的圆心角为72°,面积为5π,则此扇形的弧长为( )
A.π
B.2π
C.3π
D.4π
B
2.如图,∠ACB是⊙O的圆周角,若⊙O的半径为6,∠ACB=45°,则扇形AOB的面积为( )
A.6π
B.9π
C.24π
D.36π
B
综合演练
3.如图,☉A、☉B、
☉C、
☉D两两不相交,且半径都是4
cm,则图中阴影部分的面积是(
)
A.8π
cm2
B.12π
cm2
C.24π
cm2
D.48π
cm2
A
B
C
D
D
4.如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC,若∠ABC=120°,OC=3,则弧BC的长为_______.
2π
综合演练
·
O
A
解:设半径OA绕轴心O逆时针
方向旋转的度数为n°.
解得
n≈90°.
因此,滑轮旋转的角度约为90°.
5、一滑轮起重机装置(如图),滑轮的半径R=10
cm,当重物上升15.7
cm时,滑轮的一条半径OA绕轴心O逆时针方向旋转多少度(假设绳索与滑轮之间没有滑动,π取3.14)?
综合演练
6、如图,圆心角为60°的扇形的半径为10
cm.求这个扇形的面积和周长.(分别精确到0.01
cm2和0.01
cm)
O
R
60°
解:∵n=60,r=10
cm,
扇形的周长为:
∴扇形的面积为:
综合演练
7.如图,正方形ABCD内接于⊙O,M为弧AD中点,连接BM,CM.
(1)求证:BM=CM;
(2)当⊙O的半径为2时,求弧BM的长.
综合演练
解:(1)∵四边形ABCD是正方形,
∴AB=CD,∴AB=CD,
∵M为AD中点,∴AM=DM,
∴AB+AM=CD+DM,即BM=CM,
∴BM=CM
(
(
(
(
(
(
(
(
(
(
(
提能训练
8.
如图,一个边长为10
cm的等边三角形模板ABC在水平桌面上绕顶点C按顺时针方向旋转到△A'B'C的位置,求顶点A从开始到结束所经过的路程为多少.
A
B
A'
B'
C
解:由图可知,顶点A经过的路程长等于
的长,
∠ACA'
=180°-∠A'CB'=120°.
∵等边三角形ABC的边长为10
cm,
∴
所在圆的半径为10
cm.
答:顶点A从开始到结束时所经过的路程为
∴
课堂总结
说一说:
1、弧长公式、扇形面积公式以及二者之间的联系是什么?
2、弓形的面积公式如何计算?
本节课你有哪些收获?
作业布置
练习:
P113页:1、3
习题24.4
P115页:1、2
https://www.21cnjy.com/help/help_extract.php
24.4
弧长和扇形面积
---第1课时
人教版
九年级上
教学目标
1.掌握弧长和扇形面积公式的探求过程.(难点)
2.会利用弧长和扇形面积的计算公式进行计算.(重点)
情境导入
问题1
如图,在运动会的4×100米比赛中,为什么每个运动员他们的起跑线不在同一处?
问题2
怎样来计算弯道的“展直长度”?
因为要保证这些弯道的“展直长度”是一样的.
合作探究
思考1:半径为R的圆,周长是多少?
O
R
思考2:下图中各圆心角所对的弧长分别是圆周长的几分之几?
O
R
180°
O
R
90°
O
R
45°
O
R
n°
探究一:弧长的计算公式
合作探究
(1)
圆心角是180°,占整个周角的
,因此它所对的弧长是圆周长的______.
(2)
圆心角是90°,占整个周角的
,因此它所对的弧长是圆周长的______.
(3)
圆心角是45°,占整个周角的
,因此它所对的弧长是圆周长的_______.
(4)
圆心角是n°,占整个周角的
,因此它所对的弧长是圆周长的_______.
合作探究
特别强调:用弧长公式进行计算时,要注意公式中n的意义:n表示1°圆心角的倍数,它是不带单位的.
★弧长公式:
例如、已知弧所对的圆周角为60°,半径是4,则弧长为
.
合作探究
大小不变时,对应的弧长与
有关,
越长,弧长越大.
圆心角
半径
半径
圆的
不变时,弧长
与
有关,
越大,弧长越大.
圆心角
半径
圆心角
总结:弧长与圆心角、半径有关.
O
●
A
B
D
C
E
F
O
●
A
B
C
D
思考3:弧长哪些因素有关?
典例精析
例1
制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算如图所示管道的展直长度L.
(结果取整数)
解:由弧长公式,可得弧AB的长:
因此所要求的展直长度L=2×700+1570=2970(mm).
答:管道的展直长度为2970
mm.
700mm
700mm
R=900mm
(
100
°
A
C
B
D
O
趁热打铁
1、有一段弯道是圆弧形的,道长是12m,弧所对的圆心角是81°,求这段圆弧的半径R(精确到0.1m).
解:根据题意得,
12=
解得,R≈8.5(m).
合作探究
探究二:扇形面积的计算公式
扇形的定义:圆的一条弧和经过这条弧的端点的两条半径所围成的图形叫做扇形.
半径
半径
O
B
A
圆心角
弧
O
B
A
扇形
如图,黄色部分是一个扇形,记作扇形OAB.
趁热打铁
断一断:下列图形是扇形吗?
√
×
×
×
√
合作探究
思考4:半径为r的圆,面积是多少?
O
r
思考5:图中各扇形面积分别是圆面积的几分之几,具体是多少呢?
合作探究
O
R
180°
O
R
90°
O
R
45°
O
R
n°
圆心角占
周角的比例
扇形面积占
圆面积的比例
扇形的
面积
=
=
=
=
合作探究
★扇形面积公式:
半径为r的圆中,圆心角为n°的扇形的面积
特别强调:
①公式中n的意义:n表示1°圆心角的倍数,
它是不带单位的;
②公式要理解记忆(即按照上面推导过程记忆).
合作探究
大小不变时,对应的扇形面积与
有关,
越长,面积越大.
圆心角
半径
半径
圆的
不变时,扇形面积
与
有关,
越大,面积越大.
圆心角
半径
圆心角
总结:扇形的面积与圆心角、半径有关.
O
●
A
B
D
C
E
F
O
●
A
B
C
D
思考6:扇形的面积与哪些因素有关?
合作探究
思考7:扇形的面积公式与弧长公式有联系吗?
A
B
O
O
趁热打铁
2.已知半径为2
cm的扇形,其弧长为
cm,则这个扇形的面积
S扇形=
.
1.已知扇形的圆心角为150°,半径为3,则这个扇形的面积
S扇形=
.
典例精析
例3
如图,水平放置的圆柱形排水管道的截面半径是0.6
m,其中水面高0.3
m,求截面上有水部分的面积.(结果保留小数点后两位)
(1)
O
.
B
A
C
思考1:截面上有水部分的面积是指图上哪一部分?
解:阴影部分.
典例精析
O.
B
A
C
D
(2)
O.
B
A
C
D
(3)
思考2:水面高0.3
m是指哪一条线段的长?这条线段应该怎样画出来?
水面高0.3
m是指线段DC的长.
作法:过点O作OD⊥AB于D,并延长OD交圆O于C.
思考3:要求图中阴影部分的面积,应该怎么办?
S阴影=S扇形OAB-
S△OAB
典例精析
∵
OC=0.6
m,
DC=0.3
m,
∴
OD=OC-
DC=0.3
m.
∴
OD=DC.
又
AD
⊥DC,
∴AD是线段OC的垂直平分线.
∴AC=AO=OC.
∴
∠AOD=60?,∠AOB=120?.
O.
B
A
C
D
解:如图,连接OA,OB,过点O作弦AB的垂线,垂足为D,交
于点C,连接AC.
典例精析
有水部分的面积:
S=S扇形OAB
-
SΔOAB
在Rt△AOD中,OA=0.6
m,OD=0.3
m,
∴AD=
m.∴AB=2AD=
m.
O.
B
A
C
D
趁热打铁
1、如图、水平放置的圆柱形排水管道的截面半径是0.6
m,其中水面高0.9
m,求截面上有水部分的面积.
O
A
B
D
C
E
解:
S=S扇形OAB
+
SΔOAB
合作探究
O
O
弓形的面积=扇形的面积±三角形的面积
S弓形=S扇形-S三角形
S弓形=S扇形+S三角形
★弓形的面积公式:
综合演练
1.某扇形的圆心角为72°,面积为5π,则此扇形的弧长为( )
A.π
B.2π
C.3π
D.4π
B
2.如图,∠ACB是⊙O的圆周角,若⊙O的半径为6,∠ACB=45°,则扇形AOB的面积为( )
A.6π
B.9π
C.24π
D.36π
B
综合演练
3.如图,☉A、☉B、
☉C、
☉D两两不相交,且半径都是4
cm,则图中阴影部分的面积是(
)
A.8π
cm2
B.12π
cm2
C.24π
cm2
D.48π
cm2
A
B
C
D
D
4.如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC,若∠ABC=120°,OC=3,则弧BC的长为_______.
2π
综合演练
·
O
A
解:设半径OA绕轴心O逆时针
方向旋转的度数为n°.
解得
n≈90°.
因此,滑轮旋转的角度约为90°.
5、一滑轮起重机装置(如图),滑轮的半径R=10
cm,当重物上升15.7
cm时,滑轮的一条半径OA绕轴心O逆时针方向旋转多少度(假设绳索与滑轮之间没有滑动,π取3.14)?
综合演练
6、如图,圆心角为60°的扇形的半径为10
cm.求这个扇形的面积和周长.(分别精确到0.01
cm2和0.01
cm)
O
R
60°
解:∵n=60,r=10
cm,
扇形的周长为:
∴扇形的面积为:
综合演练
7.如图,正方形ABCD内接于⊙O,M为弧AD中点,连接BM,CM.
(1)求证:BM=CM;
(2)当⊙O的半径为2时,求弧BM的长.
综合演练
解:(1)∵四边形ABCD是正方形,
∴AB=CD,∴AB=CD,
∵M为AD中点,∴AM=DM,
∴AB+AM=CD+DM,即BM=CM,
∴BM=CM
(
(
(
(
(
(
(
(
(
(
(
提能训练
8.
如图,一个边长为10
cm的等边三角形模板ABC在水平桌面上绕顶点C按顺时针方向旋转到△A'B'C的位置,求顶点A从开始到结束所经过的路程为多少.
A
B
A'
B'
C
解:由图可知,顶点A经过的路程长等于
的长,
∠ACA'
=180°-∠A'CB'=120°.
∵等边三角形ABC的边长为10
cm,
∴
所在圆的半径为10
cm.
答:顶点A从开始到结束时所经过的路程为
∴
课堂总结
说一说:
1、弧长公式、扇形面积公式以及二者之间的联系是什么?
2、弓形的面积公式如何计算?
本节课你有哪些收获?
作业布置
练习:
P113页:1、3
习题24.4
P115页:1、2
https://www.21cnjy.com/help/help_extract.php
同课章节目录
