第7章三角函数单元 综合测试-【新教材】人教B版(2019)高中数学必修第三册(word含答案解析)
文档属性
| 名称 | 第7章三角函数单元 综合测试-【新教材】人教B版(2019)高中数学必修第三册(word含答案解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-25 12:49:13 | ||
图片预览

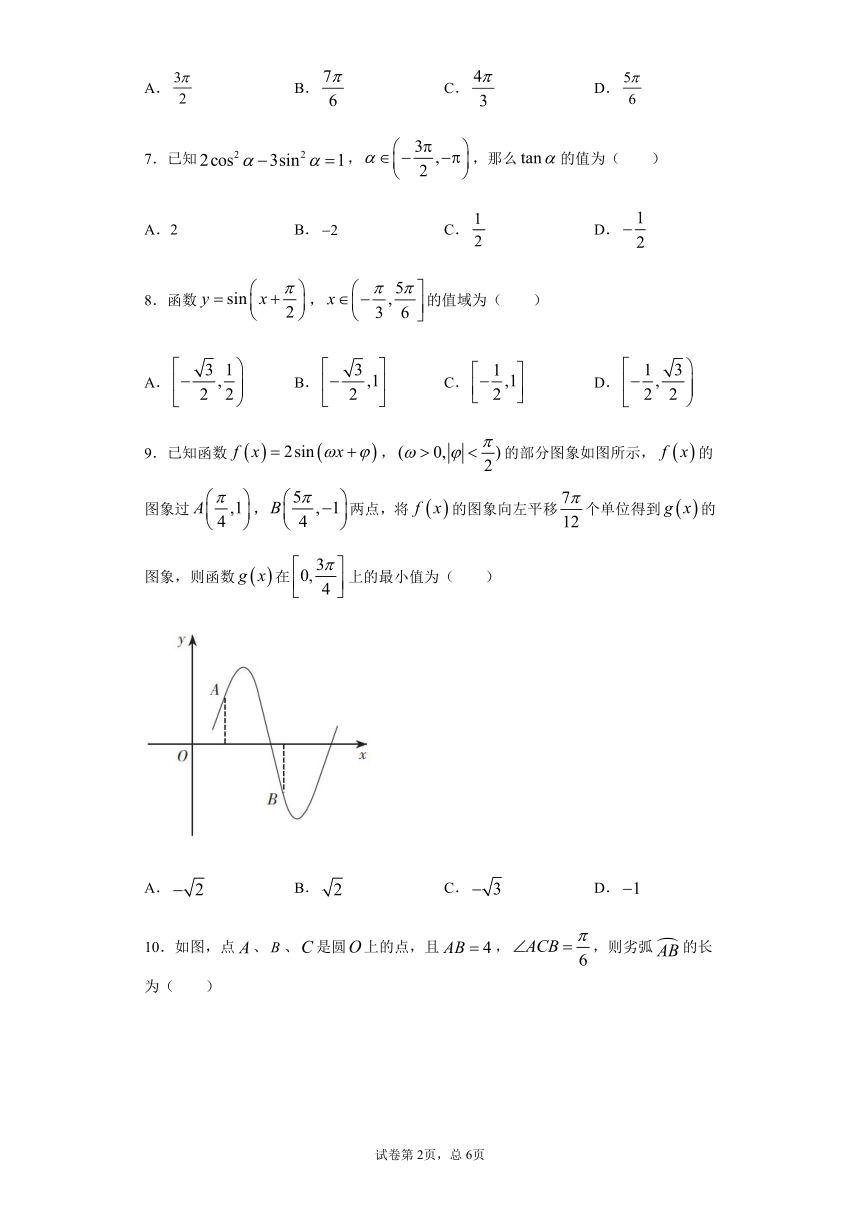


文档简介
人教B版(2019)第七章三角函数单元综合测试题
一、单选题
1.已知角的顶点与平面直角坐标系的原点重合,始边与x轴的非负半轴重合,终边经过点,则的值是
A.
B.
C.
D.
2.若为第二象限角,下列结论错误的是(
)
A.
B.
C.
D.
3.要得到函数的图象,只需将函数的图象(
)
A.向左平移个单位长度
B.向右平移个单位长度
C.向左平移个单位长度
D.向右平移个单位长度
4.若,则角是(
)
A.第一象限角
B.第二象限角
C.第三象限角
D.第四象限角
5.已知函数,,且,则的值为(
)
A.3
B.4
C.5
D.6
6.已知函数的定义域为,值域为,则的值不可能是(
)
A.
B.
C.
D.
7.已知,,那么的值为(
)
A.2
B.
C.
D.
8.函数,的值域为(
)
A.
B.
C.
D.
9.已知函数,的部分图象如图所示,的图象过,两点,将的图象向左平移个单位得到的图象,则函数在上的最小值为(
)
A.
B.
C.
D.
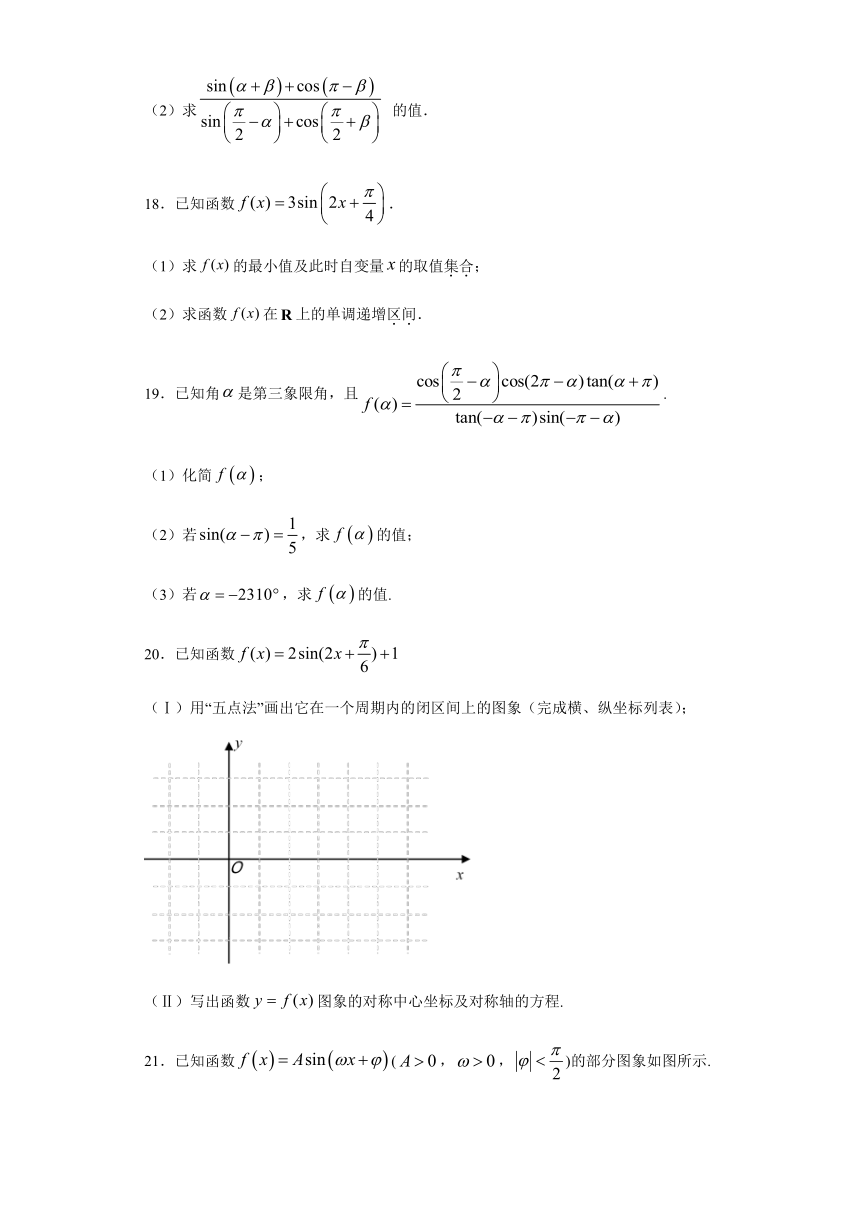
10.如图,点、、是圆上的点,且,,则劣弧的长为(
)
A.
B.
C.
D.
11.已知,则(
)
A.
B.
C.
D.
12.已知函数,则下列结论正确的个数是(
)
①的最小值为;
②点是的图象的一个对称中心;
③的最小正周期为;
④在上单调递增.
A.
B.
C.
D.
二、填空题
13.已知,则________.
14.函数在一个周期内的图象如图所示,则此函数的解析式______.
15.设函数的最大值为,最小值为,则_________.
16.若将函数的图象向左平移个单位长度,得到函数的图象,则下列说法正确的是_________.
①的最小正周期为
②在区间上单调递减
③不是函数图象的对称轴
④在上的最小值为
三、解答题
17.在平面直角坐标系中,角,β
的顶点与坐标原点重合,始边为
的非负半轴,终边分别与单位圆交于两点,两点的纵坐标分别为
(1)求的值;
(2)求
的值.
18.已知函数.
(1)求的最小值及此时自变量的取值集合;
(2)求函数在上的单调递增区间.
19.已知角是第三象限角,且.
(1)化简;
(2)若,求的值;
(3)若,求的值.
20.已知函数
(Ⅰ)用“五点法”画出它在一个周期内的闭区间上的图象(完成横、纵坐标列表);
(Ⅱ)写出函数图象的对称中心坐标及对称轴的方程.
21.已知函数(,,)的部分图象如图所示.
(1)求函数的解析式;
(2)将函数的图象向右平移个单位长度,再将得到的图象上各点的横坐标缩短为原来的,纵坐标不变,得到函数的图象,若函数在上单调递增,当实数取最大值时,求函数在上的最大值.
22.已知函数只能满足下列三个条件中的两个:①函数的最大值为;②函数的图象可由的图象平移得到;③函数图象的相邻两条对称轴之间的距离为
(1)请写出满足的这两个条件序号,并说明理由;
(2)求出的解析式;
(3)求方程在区间上所有解的和.
参考答案
1.D
【分析】
根据三角函数的基本定义,求得结果.
【详解】
由题意可知:
本题正确选项:
【点睛】
本题考查三角函数的定义,属于基础题.
2.D
【分析】
根据角所在象限,判断三角函数符号,即可判断选项.
【详解】
因为为第二象限角,
所以,,
A,B,C对,D不一定正确.
故选:D
【点睛】
本题考查了三角函数在第二象限的符号,属于基础题.
3.B
【分析】
用诱导公式把两个函数的名称化为相同,再凑配成图形变换的形式.
【详解】
由,
,
则,解得,
则只需将函数的图象向右平移个单位长度可得到函数的图象.
故选:B.
【点睛】
本题考查三角函数图象平移变换,解题时要注意两函数名称必须化为相同,才便于求解.
4.A
【分析】
根据余弦函数、正切函数的正负性的性质进行求解即可.
【详解】
因为,所以角的终边可能位于第一或第四象限,也可能与横轴的正半轴重合;
又因为,所以角的终边可能位于第一或第三象限.
因为同时成立,所以角的终边只能位于第一象限.
于是角是第一象限角.
故选:A
【点睛】
本题考查了余弦函数和正切函数的正负性的性质,属于基础题.
5.C
【分析】
由已知求得,即可得,
【详解】
由,
得
,
即,
则
.
故选:C
【点睛】
本题主要考查诱导公式化简求值,意在考查学生对这些知识的理解掌握水平.
6.A
【分析】
由题可得,观察函数图象得出的最大值和最小值即可判断.
【详解】
的定义域为,值域为,
则,则观察函数图象可得,
的最大值为,的最小值为,
,故不可能是.
故选:A.
7.D
【分析】
利用同角三角函数的基本关系即可求解.
【详解】
,
解得,所以,
即,
又,所以,
所以.
故选:D
8.B
【分析】
由诱导公式化简函数后,结合余弦函数性质求解.
【详解】
由已知,又,∴.
故选:B
9.A
【分析】
根据的图象过,两点,求得周期,进而求得,然后将点的坐标代入求得,再
将的图象向左平移个单位得到函数,利用余弦函数的单调性求解.
【详解】
由图象知,,
∴,则,
∴,
将点的坐标代入得,,即,
又,∴,
则,
将的图象向左平移个单位得到函数,
∴在上的最小值为,
故选:A
10.A
【分析】
求出以及圆的半径,利用扇形的弧长公式可求得劣弧的长.
【详解】
连接、,如下图所示:
由圆的几何性质可得,又,所以,为等边三角形,
所以圆的半径为,因此,劣弧的长为.
故选:A.
11.C
【分析】
将等式两边平方可求得的值,利用切化弦可求得的值.
【详解】
由,可得,得,
因此,.
故选:C.
【点睛】
方法点睛:应用公式时注意方程思想的应用,对于、、这三个式子,利用可以知一求二.
12.C
【分析】
求出可判断①的正误;利用正弦型函数的对称性可判断②的正误;求出的最小正周期可判断③的正误;利用正弦型函数的单调性可判断④的正误.
【详解】
对于①,,,①正确;
对于②,,
所以,点不是的图象的一个对称中心,②错误;
对于③,函数的最小正周期为,③正确;
对于④,当时,,所以,函数在上单调递增.
④正确.
因此,正确命题的序号为①③④.
故选:C.
【点睛】
关键点点睛:对于正弦型函数基本性质的判断问题,一般将函数解析式化为或,将视为一个整体,利用正弦函数或余弦函数的基本性质来求解.
13.
【分析】
根据诱导公式化简式子,再代入,求值.
【详解】
原式.
故答案为:
14.
【分析】
由五点法求得周期,由振幅可求A,再由最低点可求得φ.
【详解】
由振幅得:
由图象可得:,
∴2,
∴y=sin(2x+φ),
当时,y=,
∴,
∴解析式为:
【点睛】
本题关键点是利用五点法确定周期与φ.
15.2
【分析】
可考虑向左平移2个单位对函数解析式进行化简,根据左右平移值域不变求解.
【详解】
,
令,则定义域为R,且,
故是奇函数,故其最大值与最小值的和为零,
所以函数的最大值与最小值的和为2,
故在函数中,.
16.①③④
【分析】
由函数图像的变换可得,结合余弦函数的周期性、单调性、对称轴等即可判断选项,得出答案.
【详解】
.
的最小正周期为,选项A正确;
当
时,
时,故在上有增有减,选项B错误;,故不是图象的一条对称轴,选项C正确;
当时,,且当,即时,取最小值,D正确.
故答案为:①③④.
【点睛】
本题考查了三角函数图像的变换、余弦函数的周期性、单调性和对称轴等基本知识,考查了运算求解能力和逻辑推理能力,属于一般题目.
17.(1);(2)
【分析】
(1)利用三角函数的定义求出和,即可求出的值.
(2)分别求出、、、,再根据三角函数诱导公式、和差公式,即可求
的值.
【详解】
解:(1)因为在平面直角坐标系中,角,β
的顶点与坐标原点重合,
终边分别与单位圆交于两点,两点的纵坐标分别为.
所以,,,,
所以.
(2)由题知,,,,
所以
,
所以
【点睛】
本题考查三角函数的定义,诱导公式与和差公式,属于基础题.
18.(1),;(2)单调递增区间为,.
【分析】
(1)根据正弦函数的性质解答即可;(2)令,,
即可解得在上的单调递增区间.
【详解】
(1),此时,,
即.
(2)显然是增函数,故令,,
得在上的单调递增区间为,.
19.(1);(2);(3).
【分析】
(1)利用三角函数诱导公式化简即可.
(2)首先根据得到,从而得到,即可得到的值.
(3)首先计算,从而得到的值.
【详解】
(1)
.
(2)∵,∴,
∵是第三象限角,
∴,
∴.
(3)∵,
∴,
∴.
20.(Ⅰ)答案见解析;(Ⅱ):,,对称轴方程为:,.
【分析】
(Ⅰ)先列表求出五点,即可画出图象;
(Ⅱ)直接观察图象即可得出.
【详解】
解:(Ⅰ)
0
x
y
1
3
1
1
图象如下:
(II)观察图象可得出,
对称中心的坐标为:,,
对称轴方程为:,.
21.(1)
;(2)
【分析】
(1)根据函数的部分图象可得及周期,再根据周期公式可求出,由五点法作图的第三个点可求出的值,从而可得函数的解析式;
(2)根据平移变换和伸缩变换的规律,可求出的解析式,再根据函数在上单调递增,可求出的最大值,再根据正弦函数的图象与性质,即可求出函数在上的最大值.
【详解】
(1)由已知可得,,所以,
所以,根据五点法作图可得,所以,
所以
(2)
将函数的图象向右平移个单位长度,可得的图象,
再将得到的图象上各点的横坐标缩短为原来的,纵坐标不变,得到函数的图象,
因为函数在上单调递增,所以,所以,的最大值为,
由,可得,所以当时,取得最大值.
故函数在上的最大值为.
【点睛】
方法点睛:确定的解析式的步骤:
(1)求,,确定函数的最大值和最小值,则,;
(2)求,确定函数的周期,则;
(3)求,常用方法有以下2种方法:
①代入法:把图象上的一个已知点代入(此时要注意该点在上升区间上还是在下降区间上)或把图象的最高点或最低点代入;
②五点法:确定值时,往往以寻找“五点法”中的特殊点作为突破口.
22.(1)满足①③,理由见解析;(2);(3).
【分析】
(1)根据条件②得出函数的最大值以及该函数图象的相邻对称轴之间的距离,进而可得出结论;
(2)根据条件①求得的值,根据条件②可求得的值,由此可确定函数的解析式;
(3)由,可得,再由可得出,可解得该方程在区间上的所有解,由此可得出结果.
【详解】
(1)若满足条件②,则函数的最大值为,①不满足,
函数图象的相邻两条对称轴之间的距离为,②不满足.
因此,函数满足条件的序号为①③;
(2)由(1)可知,,函数的最小正周期为,,
所以,;
(3)由,可得.
,则,
所以,或或或,
解得或或或,
因此,方程在区间上所有解的和为.
【点睛】
方法点睛:通过求所求角的某种三角函数值来求角,关键点在选取函数,常遵照以下原则:
①已知正切函数值,选正切函数;
②已知正、余弦函数值,选正弦或余弦函数;若角的范围是,选正、余弦皆可;若角的范围是,选余弦较好;若角的范围为,选正弦较好.
试卷第1页,总3页
一、单选题
1.已知角的顶点与平面直角坐标系的原点重合,始边与x轴的非负半轴重合,终边经过点,则的值是
A.
B.
C.
D.
2.若为第二象限角,下列结论错误的是(
)
A.
B.
C.
D.
3.要得到函数的图象,只需将函数的图象(
)
A.向左平移个单位长度
B.向右平移个单位长度
C.向左平移个单位长度
D.向右平移个单位长度
4.若,则角是(
)
A.第一象限角
B.第二象限角
C.第三象限角
D.第四象限角
5.已知函数,,且,则的值为(
)
A.3
B.4
C.5
D.6
6.已知函数的定义域为,值域为,则的值不可能是(
)
A.
B.
C.
D.
7.已知,,那么的值为(
)
A.2
B.
C.
D.
8.函数,的值域为(
)
A.
B.
C.
D.
9.已知函数,的部分图象如图所示,的图象过,两点,将的图象向左平移个单位得到的图象,则函数在上的最小值为(
)
A.
B.
C.
D.
10.如图,点、、是圆上的点,且,,则劣弧的长为(
)
A.
B.
C.
D.
11.已知,则(
)
A.
B.
C.
D.
12.已知函数,则下列结论正确的个数是(
)
①的最小值为;
②点是的图象的一个对称中心;
③的最小正周期为;
④在上单调递增.
A.
B.
C.
D.
二、填空题
13.已知,则________.
14.函数在一个周期内的图象如图所示,则此函数的解析式______.
15.设函数的最大值为,最小值为,则_________.
16.若将函数的图象向左平移个单位长度,得到函数的图象,则下列说法正确的是_________.
①的最小正周期为
②在区间上单调递减
③不是函数图象的对称轴
④在上的最小值为
三、解答题
17.在平面直角坐标系中,角,β
的顶点与坐标原点重合,始边为
的非负半轴,终边分别与单位圆交于两点,两点的纵坐标分别为
(1)求的值;
(2)求
的值.
18.已知函数.
(1)求的最小值及此时自变量的取值集合;
(2)求函数在上的单调递增区间.
19.已知角是第三象限角,且.
(1)化简;
(2)若,求的值;
(3)若,求的值.
20.已知函数
(Ⅰ)用“五点法”画出它在一个周期内的闭区间上的图象(完成横、纵坐标列表);
(Ⅱ)写出函数图象的对称中心坐标及对称轴的方程.
21.已知函数(,,)的部分图象如图所示.
(1)求函数的解析式;
(2)将函数的图象向右平移个单位长度,再将得到的图象上各点的横坐标缩短为原来的,纵坐标不变,得到函数的图象,若函数在上单调递增,当实数取最大值时,求函数在上的最大值.
22.已知函数只能满足下列三个条件中的两个:①函数的最大值为;②函数的图象可由的图象平移得到;③函数图象的相邻两条对称轴之间的距离为
(1)请写出满足的这两个条件序号,并说明理由;
(2)求出的解析式;
(3)求方程在区间上所有解的和.
参考答案
1.D
【分析】
根据三角函数的基本定义,求得结果.
【详解】
由题意可知:
本题正确选项:
【点睛】
本题考查三角函数的定义,属于基础题.
2.D
【分析】
根据角所在象限,判断三角函数符号,即可判断选项.
【详解】
因为为第二象限角,
所以,,
A,B,C对,D不一定正确.
故选:D
【点睛】
本题考查了三角函数在第二象限的符号,属于基础题.
3.B
【分析】
用诱导公式把两个函数的名称化为相同,再凑配成图形变换的形式.
【详解】
由,
,
则,解得,
则只需将函数的图象向右平移个单位长度可得到函数的图象.
故选:B.
【点睛】
本题考查三角函数图象平移变换,解题时要注意两函数名称必须化为相同,才便于求解.
4.A
【分析】
根据余弦函数、正切函数的正负性的性质进行求解即可.
【详解】
因为,所以角的终边可能位于第一或第四象限,也可能与横轴的正半轴重合;
又因为,所以角的终边可能位于第一或第三象限.
因为同时成立,所以角的终边只能位于第一象限.
于是角是第一象限角.
故选:A
【点睛】
本题考查了余弦函数和正切函数的正负性的性质,属于基础题.
5.C
【分析】
由已知求得,即可得,
【详解】
由,
得
,
即,
则
.
故选:C
【点睛】
本题主要考查诱导公式化简求值,意在考查学生对这些知识的理解掌握水平.
6.A
【分析】
由题可得,观察函数图象得出的最大值和最小值即可判断.
【详解】
的定义域为,值域为,
则,则观察函数图象可得,
的最大值为,的最小值为,
,故不可能是.
故选:A.
7.D
【分析】
利用同角三角函数的基本关系即可求解.
【详解】
,
解得,所以,
即,
又,所以,
所以.
故选:D
8.B
【分析】
由诱导公式化简函数后,结合余弦函数性质求解.
【详解】
由已知,又,∴.
故选:B
9.A
【分析】
根据的图象过,两点,求得周期,进而求得,然后将点的坐标代入求得,再
将的图象向左平移个单位得到函数,利用余弦函数的单调性求解.
【详解】
由图象知,,
∴,则,
∴,
将点的坐标代入得,,即,
又,∴,
则,
将的图象向左平移个单位得到函数,
∴在上的最小值为,
故选:A
10.A
【分析】
求出以及圆的半径,利用扇形的弧长公式可求得劣弧的长.
【详解】
连接、,如下图所示:
由圆的几何性质可得,又,所以,为等边三角形,
所以圆的半径为,因此,劣弧的长为.
故选:A.
11.C
【分析】
将等式两边平方可求得的值,利用切化弦可求得的值.
【详解】
由,可得,得,
因此,.
故选:C.
【点睛】
方法点睛:应用公式时注意方程思想的应用,对于、、这三个式子,利用可以知一求二.
12.C
【分析】
求出可判断①的正误;利用正弦型函数的对称性可判断②的正误;求出的最小正周期可判断③的正误;利用正弦型函数的单调性可判断④的正误.
【详解】
对于①,,,①正确;
对于②,,
所以,点不是的图象的一个对称中心,②错误;
对于③,函数的最小正周期为,③正确;
对于④,当时,,所以,函数在上单调递增.
④正确.
因此,正确命题的序号为①③④.
故选:C.
【点睛】
关键点点睛:对于正弦型函数基本性质的判断问题,一般将函数解析式化为或,将视为一个整体,利用正弦函数或余弦函数的基本性质来求解.
13.
【分析】
根据诱导公式化简式子,再代入,求值.
【详解】
原式.
故答案为:
14.
【分析】
由五点法求得周期,由振幅可求A,再由最低点可求得φ.
【详解】
由振幅得:
由图象可得:,
∴2,
∴y=sin(2x+φ),
当时,y=,
∴,
∴解析式为:
【点睛】
本题关键点是利用五点法确定周期与φ.
15.2
【分析】
可考虑向左平移2个单位对函数解析式进行化简,根据左右平移值域不变求解.
【详解】
,
令,则定义域为R,且,
故是奇函数,故其最大值与最小值的和为零,
所以函数的最大值与最小值的和为2,
故在函数中,.
16.①③④
【分析】
由函数图像的变换可得,结合余弦函数的周期性、单调性、对称轴等即可判断选项,得出答案.
【详解】
.
的最小正周期为,选项A正确;
当
时,
时,故在上有增有减,选项B错误;,故不是图象的一条对称轴,选项C正确;
当时,,且当,即时,取最小值,D正确.
故答案为:①③④.
【点睛】
本题考查了三角函数图像的变换、余弦函数的周期性、单调性和对称轴等基本知识,考查了运算求解能力和逻辑推理能力,属于一般题目.
17.(1);(2)
【分析】
(1)利用三角函数的定义求出和,即可求出的值.
(2)分别求出、、、,再根据三角函数诱导公式、和差公式,即可求
的值.
【详解】
解:(1)因为在平面直角坐标系中,角,β
的顶点与坐标原点重合,
终边分别与单位圆交于两点,两点的纵坐标分别为.
所以,,,,
所以.
(2)由题知,,,,
所以
,
所以
【点睛】
本题考查三角函数的定义,诱导公式与和差公式,属于基础题.
18.(1),;(2)单调递增区间为,.
【分析】
(1)根据正弦函数的性质解答即可;(2)令,,
即可解得在上的单调递增区间.
【详解】
(1),此时,,
即.
(2)显然是增函数,故令,,
得在上的单调递增区间为,.
19.(1);(2);(3).
【分析】
(1)利用三角函数诱导公式化简即可.
(2)首先根据得到,从而得到,即可得到的值.
(3)首先计算,从而得到的值.
【详解】
(1)
.
(2)∵,∴,
∵是第三象限角,
∴,
∴.
(3)∵,
∴,
∴.
20.(Ⅰ)答案见解析;(Ⅱ):,,对称轴方程为:,.
【分析】
(Ⅰ)先列表求出五点,即可画出图象;
(Ⅱ)直接观察图象即可得出.
【详解】
解:(Ⅰ)
0
x
y
1
3
1
1
图象如下:
(II)观察图象可得出,
对称中心的坐标为:,,
对称轴方程为:,.
21.(1)
;(2)
【分析】
(1)根据函数的部分图象可得及周期,再根据周期公式可求出,由五点法作图的第三个点可求出的值,从而可得函数的解析式;
(2)根据平移变换和伸缩变换的规律,可求出的解析式,再根据函数在上单调递增,可求出的最大值,再根据正弦函数的图象与性质,即可求出函数在上的最大值.
【详解】
(1)由已知可得,,所以,
所以,根据五点法作图可得,所以,
所以
(2)
将函数的图象向右平移个单位长度,可得的图象,
再将得到的图象上各点的横坐标缩短为原来的,纵坐标不变,得到函数的图象,
因为函数在上单调递增,所以,所以,的最大值为,
由,可得,所以当时,取得最大值.
故函数在上的最大值为.
【点睛】
方法点睛:确定的解析式的步骤:
(1)求,,确定函数的最大值和最小值,则,;
(2)求,确定函数的周期,则;
(3)求,常用方法有以下2种方法:
①代入法:把图象上的一个已知点代入(此时要注意该点在上升区间上还是在下降区间上)或把图象的最高点或最低点代入;
②五点法:确定值时,往往以寻找“五点法”中的特殊点作为突破口.
22.(1)满足①③,理由见解析;(2);(3).
【分析】
(1)根据条件②得出函数的最大值以及该函数图象的相邻对称轴之间的距离,进而可得出结论;
(2)根据条件①求得的值,根据条件②可求得的值,由此可确定函数的解析式;
(3)由,可得,再由可得出,可解得该方程在区间上的所有解,由此可得出结果.
【详解】
(1)若满足条件②,则函数的最大值为,①不满足,
函数图象的相邻两条对称轴之间的距离为,②不满足.
因此,函数满足条件的序号为①③;
(2)由(1)可知,,函数的最小正周期为,,
所以,;
(3)由,可得.
,则,
所以,或或或,
解得或或或,
因此,方程在区间上所有解的和为.
【点睛】
方法点睛:通过求所求角的某种三角函数值来求角,关键点在选取函数,常遵照以下原则:
①已知正切函数值,选正切函数;
②已知正、余弦函数值,选正弦或余弦函数;若角的范围是,选正、余弦皆可;若角的范围是,选余弦较好;若角的范围为,选正弦较好.
试卷第1页,总3页
