5.4统计与概率的应用知识基础练 2020-2021学年高一上学期数学人教B版(2019)必修第二册第五章(Word版,含解析)
文档属性
| 名称 | 5.4统计与概率的应用知识基础练 2020-2021学年高一上学期数学人教B版(2019)必修第二册第五章(Word版,含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 304.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-25 00:00:00 | ||
图片预览



文档简介
5.4 统计与概率的应用
必备知识基础练
1.2019年4月20日,辽宁省人民政府公布了“3+1+2”新高考方案,方案中“2”指的是在思想政治、地理、化学、生物4门中选择2门.“2”中记入高考总分的单科成绩是由原始分转化得到的等级分,学科高考原始分在全省的排名越靠前,等级分越高.小明同学是2018级的学生.已确定了必选地理且不选政治,为确定另选一科,小明收集并整理了生物与化学近10大联考的成绩百分比排名数据x(如x=19的含义是指在该次考试中,成绩高于小明的考生占参加该次考试的考生数的19%)绘制茎叶图如下.
则由图中数据生物学科联考百分比排名的25%分位数为________.从平均数的角度来看你认为小明更应该选择________.(填生物或化学)
2.甲、乙两位同学参加数学文化知识竞赛培训.现分别从他们在培训期间参加的若干次测试成绩中随机抽取8次,记录如下:
甲:82 81 79 78 95 88 93 84
乙:92 95 80 75 83 80 90 85
现要从中选派一人参加正式比赛,从所抽取的两组数据分析,你认为选派哪位同学参加较为合适?并说明理由.
3.已知高二某班学生语文与数学的学业水平测试成绩抽样统计如表:
语文成绩x人数数学成绩y
A
B
C
A
7
20
5
B
9
18
6
C
a
4
b
若抽取学生n人,成绩分为A(优秀),B(良好),C(及格)三个等级,设x,y分别表示语文成绩与数学成绩,例如:表中语文成绩为B等级的共有20+18+4=42(人).设该样本中,x与y均为B等级的概率是18%,语文成绩优秀率是30%,则a+b=________,a=________,b=________.
4.如图所示,有两个可以自由转动的均匀转盘A,B.转盘A被平均分成三份,分别标上1,2,3三个数字;转盘B被平均分成四份,分别标上3,4,5,6四个数字.有人为甲、乙两人设计了一个游戏规则:自由转动转盘A与B,转盘停止后,指针各指向一个数字,将指针所指的两个数字相加,如果和是6,那么甲获胜;否则乙获胜.你认为这个游戏规则公平吗?如果公平,请说明理由;如果不公平,怎样修改规则才能使游戏对双方都公平?
5.设有外形完全相同的两个箱子,甲箱中有99个白球1个黑球,乙箱中有1个白球99个黑球.随机地抽取一箱,再从取出的一箱中抽取一球,结果取得白球,我们可以认为这球是从________箱中取出的.
6.为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行分层抽样调查,测得身高情况的统计图如下:
(1)求该校男生的人数;
(2)估计该校学生身高在170~185
cm之间的概率;
(3)从样本中身高在180~190
cm之间的男生中任选2人,求至少有1人身高在185~190
cm之间的概率.
关键能力综合练
一、选择题
1.某省在校中学生近视率约为37.4%,某配镜商要到一中学给学生配镜,若已知该校学生总数为600人,则该眼镜商应带眼镜的数目为( )
A.374副
B.224副
C.不少于225副
D.不多于225副
2.某公司员工对户外运动分别持“喜欢”“不喜欢”和“一般”三种态度,其中持“一般”态度的比持“不喜欢”态度的多12人,按分层抽样方法从该公司全体员工中选出部分员工座谈户外运动,如果选出的人有6位对户外运动持“喜欢”态度,有1位对户外运动持“不喜欢”态度,有3位对户外运动持“一般”态度,那么这个公司全体员工中对户外运动持“喜欢”态度的有( )
A.36人
B.30人
C.24人
D.18人
3.在如图所示的一组数据的茎叶图中,有一个数字被污染后模糊不清,但曾计算得该组数据的极差与25%分位数之和为56,则被污染的数字为( )
A.2
B.3
C.4
D.5
4.甲在微信群中发布6元“拼手气”红包一个,被乙、丙、丁三人抢完.若三人均领到整数元,且每人至少领到1元,则乙获得“手气最佳”(即乙领取的钱数不少于其他任何人)的概率是( )
A.
B.
C.
D.
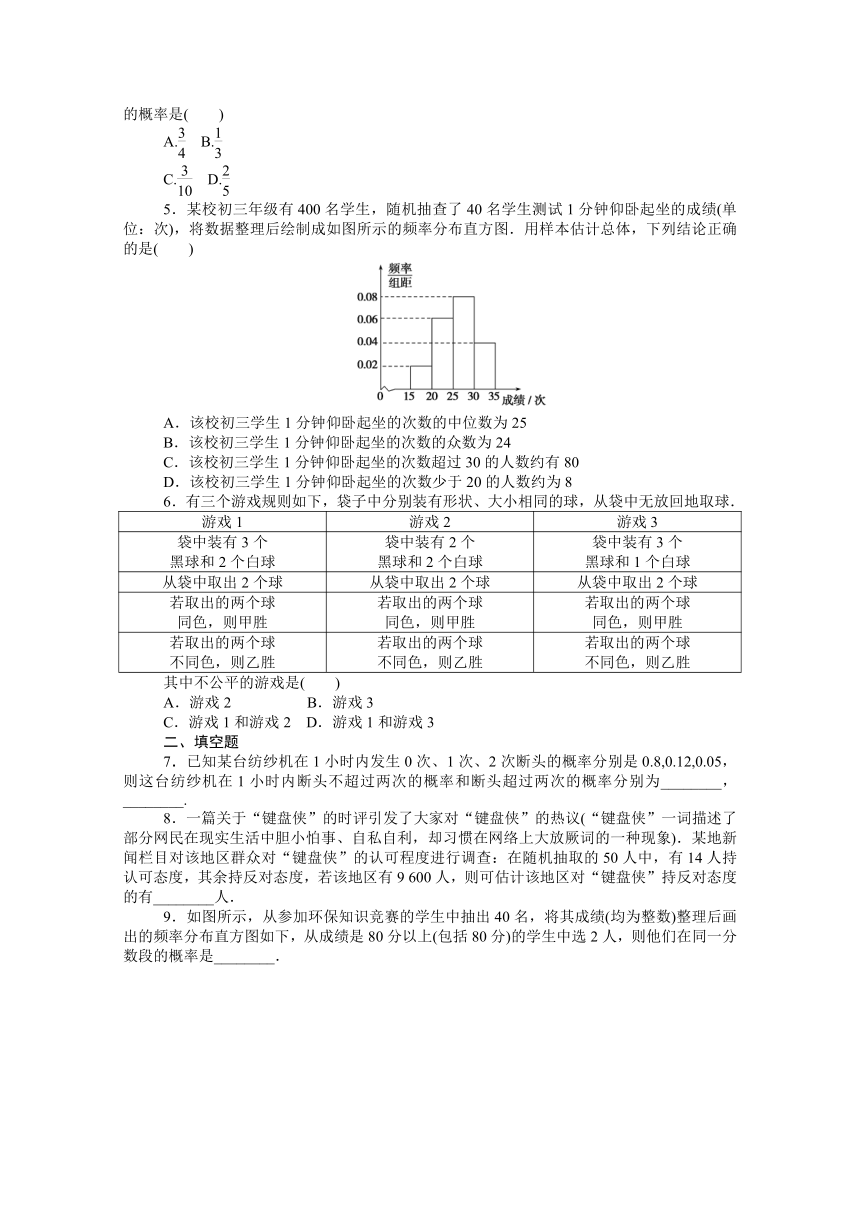
5.某校初三年级有400名学生,随机抽查了40名学生测试1分钟仰卧起坐的成绩(单位:次),将数据整理后绘制成如图所示的频率分布直方图.用样本估计总体,下列结论正确的是( )
A.该校初三学生1分钟仰卧起坐的次数的中位数为25
B.该校初三学生1分钟仰卧起坐的次数的众数为24
C.该校初三学生1分钟仰卧起坐的次数超过30的人数约有80
D.该校初三学生1分钟仰卧起坐的次数少于20的人数约为8
6.有三个游戏规则如下,袋子中分别装有形状、大小相同的球,从袋中无放回地取球.
游戏1
游戏2
游戏3
袋中装有3个黑球和2个白球
袋中装有2个黑球和2个白球
袋中装有3个黑球和1个白球
从袋中取出2个球
从袋中取出2个球
从袋中取出2个球
若取出的两个球同色,则甲胜
若取出的两个球同色,则甲胜
若取出的两个球同色,则甲胜
若取出的两个球不同色,则乙胜
若取出的两个球不同色,则乙胜
若取出的两个球不同色,则乙胜
其中不公平的游戏是( )
A.游戏2
B.游戏3
C.游戏1和游戏2
D.游戏1和游戏3
二、填空题
7.已知某台纺纱机在1小时内发生0次、1次、2次断头的概率分别是0.8,0.12,0.05,则这台纺纱机在1小时内断头不超过两次的概率和断头超过两次的概率分别为________,________.
8.一篇关于“键盘侠”的时评引发了大家对“键盘侠”的热议(“键盘侠”一词描述了部分网民在现实生活中胆小怕事、自私自利,却习惯在网络上大放厥词的一种现象).某地新闻栏目对该地区群众对“键盘侠”的认可程度进行调查:在随机抽取的50人中,有14人持认可态度,其余持反对态度,若该地区有9
600人,则可估计该地区对“键盘侠”持反对态度的有________人.
9.如图所示,从参加环保知识竞赛的学生中抽出40名,将其成绩(均为整数)整理后画出的频率分布直方图如下,从成绩是80分以上(包括80分)的学生中选2人,则他们在同一分数段的概率是________.
三、解答题
10.(探究题)甲、乙两人在相同条件下各射击10次,每次中靶环数情况如图所示.
(1)请填写下表(写出计算过程):
平均数
方差
命中9环及9环以上的次数
甲
乙
(2)从下列三个不同的角度对这次测试结果进行分析:
①从平均数和方差相结合看(分析谁的成绩更稳定);
②从平均数和命中9环及9环以上的次数相结合看(分析谁的成绩好些);
③从折线图上两人射击命中环数的走势看(分析谁更有潜力).
学科素养升级练
1.(多选题)设集合M={2,3,4},N={1,2,3,4},分别从集合M和N中随机取一个元素m与n.记“点P(m,n)落在直线x+y=k上”为事件Ak(3≤k≤8,k∈N
),若事件Ak的概率最大,则k的取值可能是( )
A.4
B.5
C.6
D.7
2.从装有4粒相同的玻璃球的瓶中,随意倒出若干粒玻璃球(至少1粒),记倒出奇数粒玻璃球的概率为P1,倒出偶数粒玻璃球的概率为P2,则( )
A.P1<P2
B.P1>P2
C.P1=P2
D.P1,P2大小不能确定
3.(学科素养—数据分析)在调查运动员服用兴奋剂的时候,给出两个问题作答,无关紧要的问题是:“你的身份证号码的尾数是奇数吗?”敏感的问题是:“你服用过兴奋剂吗?”然后要求被调查的运动员掷一枚硬币,如果出现正面向上,就回答第一个问题,否则回答第二个问题.
由于回答哪一个问题只有被测试者自己知道,所以应答者一般乐意如实地回答问题.
如我们把这种方法用于300个被调查的运动员,得到80个“是”的回答,试估计这群人中服用过兴奋剂的百分率.
5.4 统计与概率的应用
必备知识基础练
1.解析:由图可知,将生物学科联考百分比排名数据按照从小到大进行排序,可得,
12,16,21,23,25,27,34,42,43,59,设25%分位数为x.
因为10×25%=2.5,所以x=21.
生物学科联考百分比排名的平均数:
=30.2;
化学学科联考百分比排名的平均数:
=29.6,
所以从平均数的角度来看,小明更应该选择化学.
故答案为:21;化学.
答案:21 化学
2.解析:派甲参赛比较合适.理由如下:
甲=×(82+81+79+78+95+88+93+84)=85,
乙=×(92+95+80+75+83+80+90+85)=85,
s=×[(78-85)2+(79-85)2+(81-85)2+(82-85)2+(84-85)2+(88-85)2+(93-85)2+(95-85)2]=35.5,
s=×[(75-85)2+(80-85)2+(80-85)2+(83-85)2+(85-85)2+(90-85)2+(92-85)2+(95-85)2]=41.
因为甲=乙,s(或派乙参赛比较合适.理由如下:从统计的角度看,甲获得85分以上(含85分)的频率为f1=,乙获得85分以上(含85分)的频率为f2==.因为f2>f1,所以派乙参赛比较合适.)
3.解析:由题意得:经,
解得n=100,a=14,a+b=31,b=17.
故答案为:31,14,17.
答案:31 14 17
4.解析:列表如下:
B
A
3
4
5
6
1
4
5
6
7
2
5
6
7
8
3
6
7
8
9
由表可知,等可能的结果有12种,和为6的结果只有3种.
因为P(和为6)==,即甲、乙获胜的概率不相等,
所以这个游戏规则不公平.
规则改为:自由转动转盘A与B,转盘停止后,指针各指向一个数字,将指针所指的两个数字相加,如果和小于等于6,那么甲获胜;否则乙获胜.此时游戏对双方都公平.
5.解析:甲箱中有99个白球1个黑球,故随机地取出一球,
得到白球的可能性是,乙箱中有1个白球99个黑球,从中任取一球,得到白球的可能性是.
由此可知,这一白球从甲箱中取出的概率比从乙箱中取出的概率大得多,
既然在一次抽样中抽到白球,当然可以认为是由概率大的箱子中取出的,
所以我们可以认为该球是从甲箱中取出的.
答案:甲
6.解析:(1)样本中男生人数为2+5+14+13+4+2=40,由分层抽样比例为10%知全校男生人数为=400.
(2)由统计图知,样本中身高在170~185
cm之间的学生有14+13+4+3+1=35(人),样本容量为70,
所以样本中学生身高在170~185
cm之间的频率f==0.5.
故由f估计该校学生身高在170~185
cm之间的概率是0.5.
(3)样本中身高在180~185
cm之间的男生有4人,设其编号为①②③④;样本中身高在185~190
cm之间的男生有2人,设其编号为⑤⑥.
从上述6人中任选2人的树状图如图所示.
故从样本中身高在180~190
cm之间的男生中任选2人的所有可能结果数为15,且每种可能性相等,至少有1人身高在185~190
cm之间的可能结果数为9,因此所求的概率是=.
关键能力综合练
1.解析:根据概率,该校近视生人数应为
37.4%×600=224.4,
结合实际情况,眼镜商应带眼镜数不少于225副.
答案:C
2.解析:设持“喜欢”“不喜欢”“一般”态度的人数分别为6x,x,3x,由题意得3x-x=12,x=6,所以持“喜欢”态度的有6x=36人.
答案:A
3.解析:由图可知,该组数据的极差为48-20=28,则该组数据的25%分位数为56-28=28,该组数据有12个,12×25%=3,设被污染的数字为x,则=28,得x=5.故选D.
答案:D
4.解析:用(x,y,z)表示乙、丙、丁抢到的红包分别为x元、y元、z元.
乙、丙、丁三人抢完6元钱的所有不同的可能结果有10种,分别为(1,1,4),(1,4,1),(4,1,1),(1,2,3),(1,3,2),(2,1,3),(2,3,1),(3,1,2),(3,2,1),(2,2,2).
乙获得“手气最佳”的所有不同的可能结果有4种,分别为(4,1,1),(3,1,2),(3,2,1),(2,2,2).
根据古典概型的概率计算公式,得乙获得“手气最佳”的概率P==.
答案:D
5.解析:第一组数据的频率为0.02×5=0.1,第二组数据的频率为0.06×5=0.3,第三组数据的频率为0.08×5=0.4,∴中位数在第三组内,设中位数为25+x,则x×0.08=0.5-0.1-0.3=0.1,∴x=1.25,∴中位数为26.25,故A错误;第三组数据所在的矩形最高,第三组数据的中间值为27.5.∴众数为27.5,B错误;1分钟仰卧起坐的次数超过30的频率为0.2,∴超过30次的人数为400×0.2=80,故C正确;1分钟仰卧起坐的次数少于20的频率为0.1,∴1分钟仰卧起坐的次数少于20的人数为400×0.1=40,故D错误.故选C.
答案:C
6.解析:对于游戏1,取出两球同色的概率为,取出两球不同色的概率为,不公平;对于游戏2,取出两球同色的概率为,取出两球不同色的概率为,不公平;对于游戏3,取出两球同色即全是黑球,概率为,取出两球不同色的概率为,公平.故选C.
答案:C
7.解析:断头不超过两次的概率P1=0.8+0.12+0.05=0.97.于是,断头超过两次的概率P2=1-P1=1-0.97=0.03.
答案:0.97 0.03
8.解析:在随机抽取的50人中,持反对态度的频率为1-=,所以可估计该地区对“键盘侠”持反对态度的有9
600×=6912(人).
答案:6
912
9.解析:记“选出的2人在同一分数段”为事件E,80~90分之间有40×0.1=4人,设为a,b,c,d;90~100分之间有40×0.05=2人,设为A,B.从这6人中选出2人,有(a,b),(a,c),(a,d),(a,A),(a,B),(b,c),(b,d),(b,A),(b,B),(c,d),(c,A),(c,B),(d,A),(d,B),(A,B),共15个基本事件,且这15个基本事件发生的可能性是相等的,其中事件E包括(a,b),(a,c),(a,d)(b,c),(b,d),(c,d),(A,B),共7个基本事件,则P(E)=.
答案:
10.解析:由题图,知
甲射击10次中靶环数分别为9,5,7,8,7,6,8,6,7,7.
将它们由小到大排列为5,6,6,7,7,7,7,8,8,9.
乙射击10次中靶环数分别为2,4,6,8,7,7,8,9,9,10.
将它们由小到大排列为2,4,6,7,7,8,8,9,9,10.
(1)甲=×(5+6×2+7×4+8×2+9)=7,
乙=×(2+4+6+7×2+8×2+9×2+10)=7,
s=×[(5-7)2+(6-7)2×2+(7-7)2×4+(8-7)2×2+(9-7)2]=×(4+2+0+2+4)=1.2,
s=×[(2-7)2+(4-7)2+(6-7)2+(7-7)2×2+(8-7)2×2+(9-7)2×2+(10-7)2]
=×(25+9+1+0+2+8+9)=5.4.
填表如下:
平均数
方差
命中9环及9环以上的次数
甲
7
1.2
1
乙
7
5.4
3
(2)①∵平均数相同,s∴甲成绩比乙稳定.
②∵平均数相同,命中9环及9环以上的次数甲比乙少,
∴乙成绩比甲好些.
③∵甲成绩在平均数上下波动,而乙处于上升势头,从第三次以后就没有比甲少的情况发生,
∴乙更有潜力.
学科素养升级练
1.解析:由题意,点P(m,n)的所有可能情况为(2,1)、(2,2)、(2,3)、(2,4)、(3,1)、(3,2)、(3,3)、(3,4)、(4,1)、(4,2)、(4,3)、(4,4),共12个基本事件,则事件A3:点P(m,n)落在直线x+y=3包含其中(2,1)共1个基本事件,所以P(A3)=;事件A4:点P(m,n)落在直线x+y=4包含其中(2,2)、(3,1)共2个基本事件,所以P(A4)=;事件A5:点P(m,n)落在直线x+y=5包含其中(2,3)、(3,2)、(4,1)共3个基本事件,所以P(A5)=;事件A6:点P(m,n)落在直线x+y=6包含其中(2,4)、(3,3)、(4,2)共3个基本事件,所以P(A6)=;事件A7:点P(m,n)落在直线x+y=7包含其中(3,4)、(4,3)共2个基本事件,所以P(A7)=;事件A8:点P(m,n)落在直线x+y=8包含其中(4,4)共1个基本事件,所以P(A8)=.综上可得,当k=5或6时,P(Ak)max=P(A5)=P(A6)=.故选BC.
答案:BC
2.解析:我们将4粒玻璃球编号为1,2,3,4号,倒出1粒有4种情况,倒出2粒有6种情况,倒出3粒有4种情况,倒出4粒有1种情况,
我们可认为基本事件总数为4+6+4+1=15,
则倒出奇数粒玻璃球的概率P1=,
倒出偶数粒玻璃球的概率P2=.
答案:B
3.解析:因为掷硬币出现正面向上的概率为,我们期望大约有150人回答第一个问题,又身份证号码的尾数是奇数或偶数是等可能的.在回答第一个问题的150人中大约有一半人,即75人回答了“是”,其中5个回答“是”的人服用过兴奋剂,因此我们估计这群人中大约有3.33%的人服用过兴奋剂.
PAGE
必备知识基础练
1.2019年4月20日,辽宁省人民政府公布了“3+1+2”新高考方案,方案中“2”指的是在思想政治、地理、化学、生物4门中选择2门.“2”中记入高考总分的单科成绩是由原始分转化得到的等级分,学科高考原始分在全省的排名越靠前,等级分越高.小明同学是2018级的学生.已确定了必选地理且不选政治,为确定另选一科,小明收集并整理了生物与化学近10大联考的成绩百分比排名数据x(如x=19的含义是指在该次考试中,成绩高于小明的考生占参加该次考试的考生数的19%)绘制茎叶图如下.
则由图中数据生物学科联考百分比排名的25%分位数为________.从平均数的角度来看你认为小明更应该选择________.(填生物或化学)
2.甲、乙两位同学参加数学文化知识竞赛培训.现分别从他们在培训期间参加的若干次测试成绩中随机抽取8次,记录如下:
甲:82 81 79 78 95 88 93 84
乙:92 95 80 75 83 80 90 85
现要从中选派一人参加正式比赛,从所抽取的两组数据分析,你认为选派哪位同学参加较为合适?并说明理由.
3.已知高二某班学生语文与数学的学业水平测试成绩抽样统计如表:
语文成绩x人数数学成绩y
A
B
C
A
7
20
5
B
9
18
6
C
a
4
b
若抽取学生n人,成绩分为A(优秀),B(良好),C(及格)三个等级,设x,y分别表示语文成绩与数学成绩,例如:表中语文成绩为B等级的共有20+18+4=42(人).设该样本中,x与y均为B等级的概率是18%,语文成绩优秀率是30%,则a+b=________,a=________,b=________.
4.如图所示,有两个可以自由转动的均匀转盘A,B.转盘A被平均分成三份,分别标上1,2,3三个数字;转盘B被平均分成四份,分别标上3,4,5,6四个数字.有人为甲、乙两人设计了一个游戏规则:自由转动转盘A与B,转盘停止后,指针各指向一个数字,将指针所指的两个数字相加,如果和是6,那么甲获胜;否则乙获胜.你认为这个游戏规则公平吗?如果公平,请说明理由;如果不公平,怎样修改规则才能使游戏对双方都公平?
5.设有外形完全相同的两个箱子,甲箱中有99个白球1个黑球,乙箱中有1个白球99个黑球.随机地抽取一箱,再从取出的一箱中抽取一球,结果取得白球,我们可以认为这球是从________箱中取出的.
6.为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行分层抽样调查,测得身高情况的统计图如下:
(1)求该校男生的人数;
(2)估计该校学生身高在170~185
cm之间的概率;
(3)从样本中身高在180~190
cm之间的男生中任选2人,求至少有1人身高在185~190
cm之间的概率.
关键能力综合练
一、选择题
1.某省在校中学生近视率约为37.4%,某配镜商要到一中学给学生配镜,若已知该校学生总数为600人,则该眼镜商应带眼镜的数目为( )
A.374副
B.224副
C.不少于225副
D.不多于225副
2.某公司员工对户外运动分别持“喜欢”“不喜欢”和“一般”三种态度,其中持“一般”态度的比持“不喜欢”态度的多12人,按分层抽样方法从该公司全体员工中选出部分员工座谈户外运动,如果选出的人有6位对户外运动持“喜欢”态度,有1位对户外运动持“不喜欢”态度,有3位对户外运动持“一般”态度,那么这个公司全体员工中对户外运动持“喜欢”态度的有( )
A.36人
B.30人
C.24人
D.18人
3.在如图所示的一组数据的茎叶图中,有一个数字被污染后模糊不清,但曾计算得该组数据的极差与25%分位数之和为56,则被污染的数字为( )
A.2
B.3
C.4
D.5
4.甲在微信群中发布6元“拼手气”红包一个,被乙、丙、丁三人抢完.若三人均领到整数元,且每人至少领到1元,则乙获得“手气最佳”(即乙领取的钱数不少于其他任何人)的概率是( )
A.
B.
C.
D.
5.某校初三年级有400名学生,随机抽查了40名学生测试1分钟仰卧起坐的成绩(单位:次),将数据整理后绘制成如图所示的频率分布直方图.用样本估计总体,下列结论正确的是( )
A.该校初三学生1分钟仰卧起坐的次数的中位数为25
B.该校初三学生1分钟仰卧起坐的次数的众数为24
C.该校初三学生1分钟仰卧起坐的次数超过30的人数约有80
D.该校初三学生1分钟仰卧起坐的次数少于20的人数约为8
6.有三个游戏规则如下,袋子中分别装有形状、大小相同的球,从袋中无放回地取球.
游戏1
游戏2
游戏3
袋中装有3个黑球和2个白球
袋中装有2个黑球和2个白球
袋中装有3个黑球和1个白球
从袋中取出2个球
从袋中取出2个球
从袋中取出2个球
若取出的两个球同色,则甲胜
若取出的两个球同色,则甲胜
若取出的两个球同色,则甲胜
若取出的两个球不同色,则乙胜
若取出的两个球不同色,则乙胜
若取出的两个球不同色,则乙胜
其中不公平的游戏是( )
A.游戏2
B.游戏3
C.游戏1和游戏2
D.游戏1和游戏3
二、填空题
7.已知某台纺纱机在1小时内发生0次、1次、2次断头的概率分别是0.8,0.12,0.05,则这台纺纱机在1小时内断头不超过两次的概率和断头超过两次的概率分别为________,________.
8.一篇关于“键盘侠”的时评引发了大家对“键盘侠”的热议(“键盘侠”一词描述了部分网民在现实生活中胆小怕事、自私自利,却习惯在网络上大放厥词的一种现象).某地新闻栏目对该地区群众对“键盘侠”的认可程度进行调查:在随机抽取的50人中,有14人持认可态度,其余持反对态度,若该地区有9
600人,则可估计该地区对“键盘侠”持反对态度的有________人.
9.如图所示,从参加环保知识竞赛的学生中抽出40名,将其成绩(均为整数)整理后画出的频率分布直方图如下,从成绩是80分以上(包括80分)的学生中选2人,则他们在同一分数段的概率是________.
三、解答题
10.(探究题)甲、乙两人在相同条件下各射击10次,每次中靶环数情况如图所示.
(1)请填写下表(写出计算过程):
平均数
方差
命中9环及9环以上的次数
甲
乙
(2)从下列三个不同的角度对这次测试结果进行分析:
①从平均数和方差相结合看(分析谁的成绩更稳定);
②从平均数和命中9环及9环以上的次数相结合看(分析谁的成绩好些);
③从折线图上两人射击命中环数的走势看(分析谁更有潜力).
学科素养升级练
1.(多选题)设集合M={2,3,4},N={1,2,3,4},分别从集合M和N中随机取一个元素m与n.记“点P(m,n)落在直线x+y=k上”为事件Ak(3≤k≤8,k∈N
),若事件Ak的概率最大,则k的取值可能是( )
A.4
B.5
C.6
D.7
2.从装有4粒相同的玻璃球的瓶中,随意倒出若干粒玻璃球(至少1粒),记倒出奇数粒玻璃球的概率为P1,倒出偶数粒玻璃球的概率为P2,则( )
A.P1<P2
B.P1>P2
C.P1=P2
D.P1,P2大小不能确定
3.(学科素养—数据分析)在调查运动员服用兴奋剂的时候,给出两个问题作答,无关紧要的问题是:“你的身份证号码的尾数是奇数吗?”敏感的问题是:“你服用过兴奋剂吗?”然后要求被调查的运动员掷一枚硬币,如果出现正面向上,就回答第一个问题,否则回答第二个问题.
由于回答哪一个问题只有被测试者自己知道,所以应答者一般乐意如实地回答问题.
如我们把这种方法用于300个被调查的运动员,得到80个“是”的回答,试估计这群人中服用过兴奋剂的百分率.
5.4 统计与概率的应用
必备知识基础练
1.解析:由图可知,将生物学科联考百分比排名数据按照从小到大进行排序,可得,
12,16,21,23,25,27,34,42,43,59,设25%分位数为x.
因为10×25%=2.5,所以x=21.
生物学科联考百分比排名的平均数:
=30.2;
化学学科联考百分比排名的平均数:
=29.6,
所以从平均数的角度来看,小明更应该选择化学.
故答案为:21;化学.
答案:21 化学
2.解析:派甲参赛比较合适.理由如下:
甲=×(82+81+79+78+95+88+93+84)=85,
乙=×(92+95+80+75+83+80+90+85)=85,
s=×[(78-85)2+(79-85)2+(81-85)2+(82-85)2+(84-85)2+(88-85)2+(93-85)2+(95-85)2]=35.5,
s=×[(75-85)2+(80-85)2+(80-85)2+(83-85)2+(85-85)2+(90-85)2+(92-85)2+(95-85)2]=41.
因为甲=乙,s
3.解析:由题意得:经,
解得n=100,a=14,a+b=31,b=17.
故答案为:31,14,17.
答案:31 14 17
4.解析:列表如下:
B
A
3
4
5
6
1
4
5
6
7
2
5
6
7
8
3
6
7
8
9
由表可知,等可能的结果有12种,和为6的结果只有3种.
因为P(和为6)==,即甲、乙获胜的概率不相等,
所以这个游戏规则不公平.
规则改为:自由转动转盘A与B,转盘停止后,指针各指向一个数字,将指针所指的两个数字相加,如果和小于等于6,那么甲获胜;否则乙获胜.此时游戏对双方都公平.
5.解析:甲箱中有99个白球1个黑球,故随机地取出一球,
得到白球的可能性是,乙箱中有1个白球99个黑球,从中任取一球,得到白球的可能性是.
由此可知,这一白球从甲箱中取出的概率比从乙箱中取出的概率大得多,
既然在一次抽样中抽到白球,当然可以认为是由概率大的箱子中取出的,
所以我们可以认为该球是从甲箱中取出的.
答案:甲
6.解析:(1)样本中男生人数为2+5+14+13+4+2=40,由分层抽样比例为10%知全校男生人数为=400.
(2)由统计图知,样本中身高在170~185
cm之间的学生有14+13+4+3+1=35(人),样本容量为70,
所以样本中学生身高在170~185
cm之间的频率f==0.5.
故由f估计该校学生身高在170~185
cm之间的概率是0.5.
(3)样本中身高在180~185
cm之间的男生有4人,设其编号为①②③④;样本中身高在185~190
cm之间的男生有2人,设其编号为⑤⑥.
从上述6人中任选2人的树状图如图所示.
故从样本中身高在180~190
cm之间的男生中任选2人的所有可能结果数为15,且每种可能性相等,至少有1人身高在185~190
cm之间的可能结果数为9,因此所求的概率是=.
关键能力综合练
1.解析:根据概率,该校近视生人数应为
37.4%×600=224.4,
结合实际情况,眼镜商应带眼镜数不少于225副.
答案:C
2.解析:设持“喜欢”“不喜欢”“一般”态度的人数分别为6x,x,3x,由题意得3x-x=12,x=6,所以持“喜欢”态度的有6x=36人.
答案:A
3.解析:由图可知,该组数据的极差为48-20=28,则该组数据的25%分位数为56-28=28,该组数据有12个,12×25%=3,设被污染的数字为x,则=28,得x=5.故选D.
答案:D
4.解析:用(x,y,z)表示乙、丙、丁抢到的红包分别为x元、y元、z元.
乙、丙、丁三人抢完6元钱的所有不同的可能结果有10种,分别为(1,1,4),(1,4,1),(4,1,1),(1,2,3),(1,3,2),(2,1,3),(2,3,1),(3,1,2),(3,2,1),(2,2,2).
乙获得“手气最佳”的所有不同的可能结果有4种,分别为(4,1,1),(3,1,2),(3,2,1),(2,2,2).
根据古典概型的概率计算公式,得乙获得“手气最佳”的概率P==.
答案:D
5.解析:第一组数据的频率为0.02×5=0.1,第二组数据的频率为0.06×5=0.3,第三组数据的频率为0.08×5=0.4,∴中位数在第三组内,设中位数为25+x,则x×0.08=0.5-0.1-0.3=0.1,∴x=1.25,∴中位数为26.25,故A错误;第三组数据所在的矩形最高,第三组数据的中间值为27.5.∴众数为27.5,B错误;1分钟仰卧起坐的次数超过30的频率为0.2,∴超过30次的人数为400×0.2=80,故C正确;1分钟仰卧起坐的次数少于20的频率为0.1,∴1分钟仰卧起坐的次数少于20的人数为400×0.1=40,故D错误.故选C.
答案:C
6.解析:对于游戏1,取出两球同色的概率为,取出两球不同色的概率为,不公平;对于游戏2,取出两球同色的概率为,取出两球不同色的概率为,不公平;对于游戏3,取出两球同色即全是黑球,概率为,取出两球不同色的概率为,公平.故选C.
答案:C
7.解析:断头不超过两次的概率P1=0.8+0.12+0.05=0.97.于是,断头超过两次的概率P2=1-P1=1-0.97=0.03.
答案:0.97 0.03
8.解析:在随机抽取的50人中,持反对态度的频率为1-=,所以可估计该地区对“键盘侠”持反对态度的有9
600×=6912(人).
答案:6
912
9.解析:记“选出的2人在同一分数段”为事件E,80~90分之间有40×0.1=4人,设为a,b,c,d;90~100分之间有40×0.05=2人,设为A,B.从这6人中选出2人,有(a,b),(a,c),(a,d),(a,A),(a,B),(b,c),(b,d),(b,A),(b,B),(c,d),(c,A),(c,B),(d,A),(d,B),(A,B),共15个基本事件,且这15个基本事件发生的可能性是相等的,其中事件E包括(a,b),(a,c),(a,d)(b,c),(b,d),(c,d),(A,B),共7个基本事件,则P(E)=.
答案:
10.解析:由题图,知
甲射击10次中靶环数分别为9,5,7,8,7,6,8,6,7,7.
将它们由小到大排列为5,6,6,7,7,7,7,8,8,9.
乙射击10次中靶环数分别为2,4,6,8,7,7,8,9,9,10.
将它们由小到大排列为2,4,6,7,7,8,8,9,9,10.
(1)甲=×(5+6×2+7×4+8×2+9)=7,
乙=×(2+4+6+7×2+8×2+9×2+10)=7,
s=×[(5-7)2+(6-7)2×2+(7-7)2×4+(8-7)2×2+(9-7)2]=×(4+2+0+2+4)=1.2,
s=×[(2-7)2+(4-7)2+(6-7)2+(7-7)2×2+(8-7)2×2+(9-7)2×2+(10-7)2]
=×(25+9+1+0+2+8+9)=5.4.
填表如下:
平均数
方差
命中9环及9环以上的次数
甲
7
1.2
1
乙
7
5.4
3
(2)①∵平均数相同,s
②∵平均数相同,命中9环及9环以上的次数甲比乙少,
∴乙成绩比甲好些.
③∵甲成绩在平均数上下波动,而乙处于上升势头,从第三次以后就没有比甲少的情况发生,
∴乙更有潜力.
学科素养升级练
1.解析:由题意,点P(m,n)的所有可能情况为(2,1)、(2,2)、(2,3)、(2,4)、(3,1)、(3,2)、(3,3)、(3,4)、(4,1)、(4,2)、(4,3)、(4,4),共12个基本事件,则事件A3:点P(m,n)落在直线x+y=3包含其中(2,1)共1个基本事件,所以P(A3)=;事件A4:点P(m,n)落在直线x+y=4包含其中(2,2)、(3,1)共2个基本事件,所以P(A4)=;事件A5:点P(m,n)落在直线x+y=5包含其中(2,3)、(3,2)、(4,1)共3个基本事件,所以P(A5)=;事件A6:点P(m,n)落在直线x+y=6包含其中(2,4)、(3,3)、(4,2)共3个基本事件,所以P(A6)=;事件A7:点P(m,n)落在直线x+y=7包含其中(3,4)、(4,3)共2个基本事件,所以P(A7)=;事件A8:点P(m,n)落在直线x+y=8包含其中(4,4)共1个基本事件,所以P(A8)=.综上可得,当k=5或6时,P(Ak)max=P(A5)=P(A6)=.故选BC.
答案:BC
2.解析:我们将4粒玻璃球编号为1,2,3,4号,倒出1粒有4种情况,倒出2粒有6种情况,倒出3粒有4种情况,倒出4粒有1种情况,
我们可认为基本事件总数为4+6+4+1=15,
则倒出奇数粒玻璃球的概率P1=,
倒出偶数粒玻璃球的概率P2=.
答案:B
3.解析:因为掷硬币出现正面向上的概率为,我们期望大约有150人回答第一个问题,又身份证号码的尾数是奇数或偶数是等可能的.在回答第一个问题的150人中大约有一半人,即75人回答了“是”,其中5个回答“是”的人服用过兴奋剂,因此我们估计这群人中大约有3.33%的人服用过兴奋剂.
PAGE
