6.1.3向量的减法知识基础练2020-2021学年高一上学期数学人教B版(2019)必修第二册第6章平面向量初步(Word版,含解析)
文档属性
| 名称 | 6.1.3向量的减法知识基础练2020-2021学年高一上学期数学人教B版(2019)必修第二册第6章平面向量初步(Word版,含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 289.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-25 09:18:36 | ||
图片预览


文档简介
6.1.3 向量的减法
必备知识基础练
1.下列各式中不能化简为的是( )
A.(-)-
B.
-(+)
C.-(+)-(+)
D.-
-+
2.在平行四边形ABCD中,--等于( )
A.
B.
C.
D.
3.如图所示,在?ABCD中,=a,=b,则用a,b表示向量和分别是( )
A.a+b和a-b
B.a+b和b-a
C.a-b和b-a
D.b-a和b+a
4.若平行四边形ABCD的对角线AC和BD相交于点O,且=a,
=b,用a,b表示向量为( )
A.a+b
B.-a-b
C.-a+b
D.a-b
5.如图,已知正方形ABCD的边长等于1,
=a,
=b,
=c,试作向量并分别求模:
(1)a+b+c;
(2)a-b+c.
6.已知||=6,||=9,求|-|的取值范围.
关键能力综合练
一、选择题
1.化简-+所得的结果是( )
A.
B.
C.0
D.
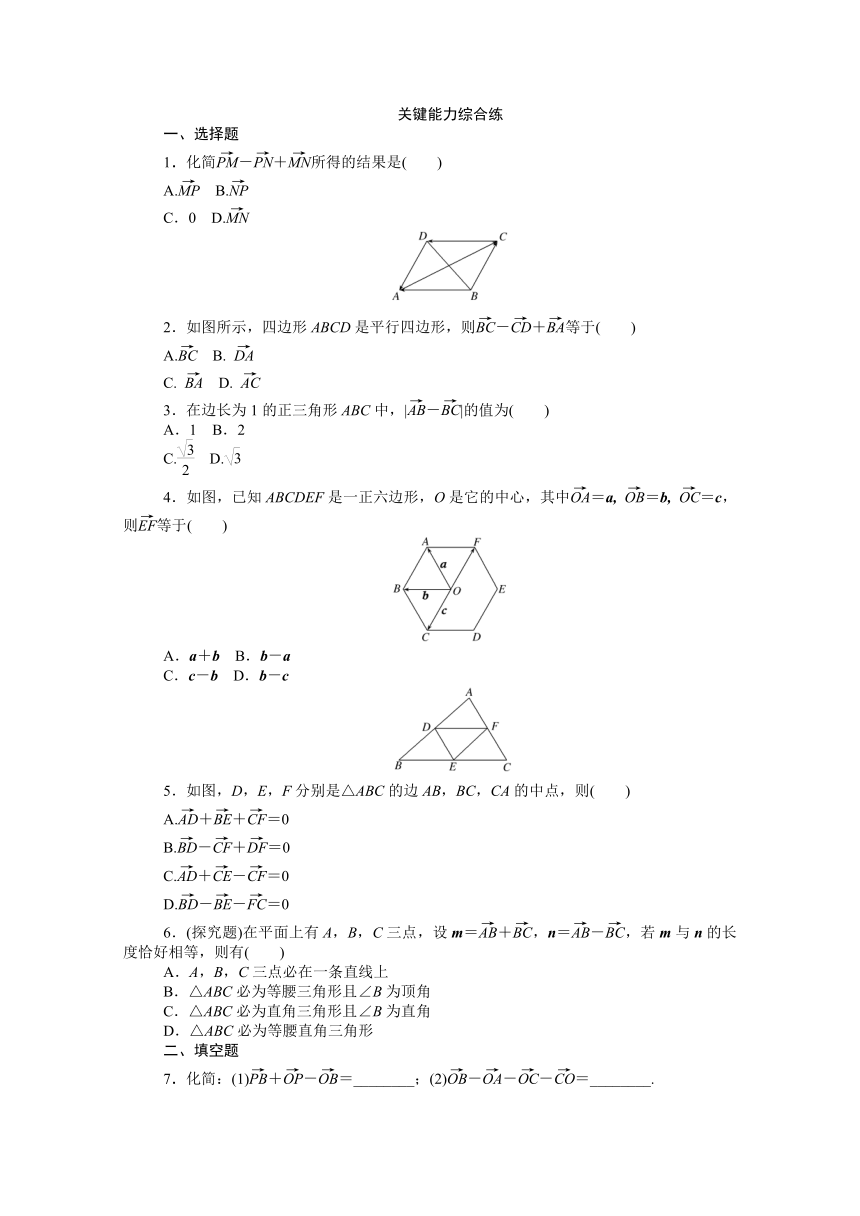
2.如图所示,四边形ABCD是平行四边形,则-+等于( )
A.
B.
C.
D.
3.在边长为1的正三角形ABC中,|-|的值为( )
A.1
B.2
C.
D.
4.如图,已知ABCDEF是一正六边形,O是它的中心,其中=a,
=b,
=c,则等于( )
A.a+b
B.b-a
C.c-b
D.b-c
5.如图,D,E,F分别是△ABC的边AB,BC,CA的中点,则( )
A.++=0
B.-+=0
C.+-=0
D.--=0
6.(探究题)在平面上有A,B,C三点,设m=+,n=-,若m与n的长度恰好相等,则有( )
A.A,B,C三点必在一条直线上
B.△ABC必为等腰三角形且∠B为顶角
C.△ABC必为直角三角形且∠B为直角
D.△ABC必为等腰直角三角形
二、填空题
7.化简:(1)+-=________;(2)---=________.
8.已知=a,=b,若||=12,||=5,且∠AOB=90°,则|a-b|的值为________.
9.(易错题)已知非零向量a,b满足|a|=|b|=|a-b|,则=________.
三、解答题
10.如图所示,已知=a,=b,=c,=e,=d,=f,试用a,b,c,d,e,f表示,,-,+,-.
学科素养升级练
1.(多选题)设a=(+)+(+),b是任一非零向量,则在下列结论中,正确的为( )
A.a∥b
B.a+b=b
C.a-b=b
D.|a-b|<|a|+|b|
2.已知菱形ABCD的边长为2,则向量-+的模为________;||的范围是________.
3.(学科素养—逻辑推理)已知△ABC是等腰直角三角形,∠ACB=90°,M是斜边AB的中点,=a,=b,求证:
(1)|a-b|=|a|;
(2)|a+(a-b)|=|b|.
6.1.3 向量的减法
必备知识基础练
1.解析:因为(-)-=++=+=;-(+)=-0=;-(+)-(+)=-(-)-(+)=---=+-=;--+=++=+2.故选D.
答案:D
2.解析:--=-=+=,又因为=,所以--=.
答案:D
3.解析:由向量的加法、减法法则,得
=+=a+b,
=-=b-a.
答案:B
4.解析:由平行四边形对角线互相平分的性质知=-,即=-a,=-=-a-b.
答案:B
5.解析:(1)如图,由已知得,a+b=+=,
又=c,∴延长AC到E,
使|
|=||.
则a+b+c=,且|
|=2.
(2)如图,作=,
则+=,
而=-=a-=a-b,
∴a-b+c=+=且||=2.
6.解析:∵|||-|||≤|-|≤||+||,且||=9,||=6,∴3≤|-|≤15.
当与同向时,|-|=3;
当与反向时,|-|=15.
∴|-|的取值范围为[3,15].
关键能力综合练
1.解析:-+=+=0.
答案:C
2.解析:-+=++=+0=.
答案:A
3.解析:
如图,作菱形ABCD,
则|-|=|-|
=||=.
答案:D
4.解析:===-=b-c.
答案:D
5.解析:++=++
=(++)=0.
答案:A
6.解析:以,为邻边作平行四边形ABCD,则m=+=,n=-=-=.由m,n的长度相等,可知两对角线相等,因此平行四边形是矩形.故选C.
答案:C
7.解析:(1)+-=+=0;
(2)---=(-)-(+)
=-0=.
答案:(1)0 (2)
8.解析:a,b,a-b构成了一个直角三角形,
则|a-b|===13.
答案:13
9.解析:如图,设=a,=b,=a+b,则=-=a-b,
∵|a|=|b|=|a-b|,
∴BA=OA=OB.
∴△OAB为正三角形,设其边长为1,
则|a-b|=||=1,|a+b|=2×=.
∴==.
答案:
10.解析:=-=c-a,
=-=d-a,
-==-=d-b,
+=-+-=b-a+f-c,
-==-=f-d.
学科素养升级练
1.解析:由题a=+++=0,又因为b为非零向量,故a∥b,a+b=b,故AB正确,又因为a-b=-b
,|a-b|=|a|+|b|,CD错误,故选AB.
答案:AB
2.解析:因为-+=++=,又||=2,所以|-+|=
||=2.又因为=+,且在菱形ABCD中||=2,所以|||-|||<
||=|+|<||+||,即0<||<4.
答案:2 (0,4)
3.证明:
如图,在等腰Rt△ABC中,由M是斜边AB的中点,
得||=||,||=||.
(1)在△ACM中,=-=a-b.
于是由||=||,
得|a-b|=|a|.
(2)在△MCB中,==a-b,
所以=-=a-b+a=a+(a-b).
从而由||=||,
得|a+(a-b)|=|b|.
PAGE
必备知识基础练
1.下列各式中不能化简为的是( )
A.(-)-
B.
-(+)
C.-(+)-(+)
D.-
-+
2.在平行四边形ABCD中,--等于( )
A.
B.
C.
D.
3.如图所示,在?ABCD中,=a,=b,则用a,b表示向量和分别是( )
A.a+b和a-b
B.a+b和b-a
C.a-b和b-a
D.b-a和b+a
4.若平行四边形ABCD的对角线AC和BD相交于点O,且=a,
=b,用a,b表示向量为( )
A.a+b
B.-a-b
C.-a+b
D.a-b
5.如图,已知正方形ABCD的边长等于1,
=a,
=b,
=c,试作向量并分别求模:
(1)a+b+c;
(2)a-b+c.
6.已知||=6,||=9,求|-|的取值范围.
关键能力综合练
一、选择题
1.化简-+所得的结果是( )
A.
B.
C.0
D.
2.如图所示,四边形ABCD是平行四边形,则-+等于( )
A.
B.
C.
D.
3.在边长为1的正三角形ABC中,|-|的值为( )
A.1
B.2
C.
D.
4.如图,已知ABCDEF是一正六边形,O是它的中心,其中=a,
=b,
=c,则等于( )
A.a+b
B.b-a
C.c-b
D.b-c
5.如图,D,E,F分别是△ABC的边AB,BC,CA的中点,则( )
A.++=0
B.-+=0
C.+-=0
D.--=0
6.(探究题)在平面上有A,B,C三点,设m=+,n=-,若m与n的长度恰好相等,则有( )
A.A,B,C三点必在一条直线上
B.△ABC必为等腰三角形且∠B为顶角
C.△ABC必为直角三角形且∠B为直角
D.△ABC必为等腰直角三角形
二、填空题
7.化简:(1)+-=________;(2)---=________.
8.已知=a,=b,若||=12,||=5,且∠AOB=90°,则|a-b|的值为________.
9.(易错题)已知非零向量a,b满足|a|=|b|=|a-b|,则=________.
三、解答题
10.如图所示,已知=a,=b,=c,=e,=d,=f,试用a,b,c,d,e,f表示,,-,+,-.
学科素养升级练
1.(多选题)设a=(+)+(+),b是任一非零向量,则在下列结论中,正确的为( )
A.a∥b
B.a+b=b
C.a-b=b
D.|a-b|<|a|+|b|
2.已知菱形ABCD的边长为2,则向量-+的模为________;||的范围是________.
3.(学科素养—逻辑推理)已知△ABC是等腰直角三角形,∠ACB=90°,M是斜边AB的中点,=a,=b,求证:
(1)|a-b|=|a|;
(2)|a+(a-b)|=|b|.
6.1.3 向量的减法
必备知识基础练
1.解析:因为(-)-=++=+=;-(+)=-0=;-(+)-(+)=-(-)-(+)=---=+-=;--+=++=+2.故选D.
答案:D
2.解析:--=-=+=,又因为=,所以--=.
答案:D
3.解析:由向量的加法、减法法则,得
=+=a+b,
=-=b-a.
答案:B
4.解析:由平行四边形对角线互相平分的性质知=-,即=-a,=-=-a-b.
答案:B
5.解析:(1)如图,由已知得,a+b=+=,
又=c,∴延长AC到E,
使|
|=||.
则a+b+c=,且|
|=2.
(2)如图,作=,
则+=,
而=-=a-=a-b,
∴a-b+c=+=且||=2.
6.解析:∵|||-|||≤|-|≤||+||,且||=9,||=6,∴3≤|-|≤15.
当与同向时,|-|=3;
当与反向时,|-|=15.
∴|-|的取值范围为[3,15].
关键能力综合练
1.解析:-+=+=0.
答案:C
2.解析:-+=++=+0=.
答案:A
3.解析:
如图,作菱形ABCD,
则|-|=|-|
=||=.
答案:D
4.解析:===-=b-c.
答案:D
5.解析:++=++
=(++)=0.
答案:A
6.解析:以,为邻边作平行四边形ABCD,则m=+=,n=-=-=.由m,n的长度相等,可知两对角线相等,因此平行四边形是矩形.故选C.
答案:C
7.解析:(1)+-=+=0;
(2)---=(-)-(+)
=-0=.
答案:(1)0 (2)
8.解析:a,b,a-b构成了一个直角三角形,
则|a-b|===13.
答案:13
9.解析:如图,设=a,=b,=a+b,则=-=a-b,
∵|a|=|b|=|a-b|,
∴BA=OA=OB.
∴△OAB为正三角形,设其边长为1,
则|a-b|=||=1,|a+b|=2×=.
∴==.
答案:
10.解析:=-=c-a,
=-=d-a,
-==-=d-b,
+=-+-=b-a+f-c,
-==-=f-d.
学科素养升级练
1.解析:由题a=+++=0,又因为b为非零向量,故a∥b,a+b=b,故AB正确,又因为a-b=-b
,|a-b|=|a|+|b|,CD错误,故选AB.
答案:AB
2.解析:因为-+=++=,又||=2,所以|-+|=
||=2.又因为=+,且在菱形ABCD中||=2,所以|||-|||<
||=|+|<||+||,即0<||<4.
答案:2 (0,4)
3.证明:
如图,在等腰Rt△ABC中,由M是斜边AB的中点,
得||=||,||=||.
(1)在△ACM中,=-=a-b.
于是由||=||,
得|a-b|=|a|.
(2)在△MCB中,==a-b,
所以=-=a-b+a=a+(a-b).
从而由||=||,
得|a+(a-b)|=|b|.
PAGE
