第6章 单元质量测评 同步习题2020-2021学年高一数学人教B版(2019)必修第二册 第6章平面向量初步(Word含答案解析)
文档属性
| 名称 | 第6章 单元质量测评 同步习题2020-2021学年高一数学人教B版(2019)必修第二册 第6章平面向量初步(Word含答案解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 433.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-25 13:05:48 | ||
图片预览




文档简介
第六章 单元质量测评
时间:120分钟 满分:150分
一、单项选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知点A(0,1),B(3,2),向量=(-4,-3),则向量=( )
A.(-7,-4)
B.(7,4)
C.(-1,4)
D.(1,4)
2.如图所示,已知=3,=3,则向量与的关系为( )
A.共线
B.同向
C.共线且同向
D.共线、同向,且的长度是的3倍
3.已知向量a=(1,1),b=(2,x),若a+b与4b-2a平行,则实数x的值是( )
A.-2
B.0
C.1
D.2
4.已知三个力f1=(-2,-1),f2=(-3,2),f3=(4,-3)同时作用于某物体上一点,为使物体保持平衡,现加上一个力f4,则f4=( )
A.(-1,-2)
B.(1,-2)
C.(-1,2)
D.(1,2)
5.已知平面内M,N,P三点满足-+=0,则下列说法正确的是( )
A.M,N,P是一个三角形的三个顶点
B.M,N,P是一条直线上的三个点
C.M,N,P是平面内的任意三个点
D.以上都不对
6.已知△ABC中,点D在BC边上,且=2,=r+s,则r+s的值是( )
A.
B.
C.-3
D.0
7.在梯形ABCD中,AB∥CD,且DC=2AB,三个顶点A(1,2),B(2,1),C(4,2),则点D的坐标为( )
A.(2,4)
B.(2,2)
C.(4,1)
D.(4,4)
8.在△ABC中,=,DE∥BC,且DE与AC相交于点E,M是BC的中点,AM与DE相交于点N.若=x+y(x,y∈R),则x+y=( )
A.1
B.
C.
D.
二、多项选择题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分)
9.
如图,在梯形ABDC中,AB∥CD,||=2||,AD与BC相交于点O,则下列结论正确的是( )
A.-=
B.+++=0
C.|+2|=0
D.=+
10.如图2,“六芒星”是由两个全等正三角形组成,中心重合于点O且三组对边分别平行,点F,B是“六芒星”(如图1)的两个顶点,动点P在“六芒星”上(内部以及边界),若=x+y,则x+y的取值可能是( )
A.-6
B.1
C.5
D.9
11.已知图中∠AOC+2∠BOC=180°,||=||,BC∥OA,P为图中的阴影中(含边界)任意点,并且=x+y,下列命题正确的是( )
A.0≤x+y≤1
B.|x|+|y|≤x2+y2
C.x2+y2≤2
D.存在无数个点P,使得y=1
12.定义平面向量之间的一种运算“⊙”如下:对任意的a=(m,n),b=(p,q),令a⊙b=mq-np,则下列说法正确的是( )
A.若a与b共线,则a⊙b=0
B.a⊙b=b⊙a
C.对任意的λ∈R,有(λa)⊙b=λ(a⊙b)
D.(a⊙b)2+(b⊙a)2=|a|2|b|2
三、填空题(本题共4小题,每小题5分,共20分.把答案填在题中的横线上)
13.△ABC所在的平面内有一点P,满足+2+=2,则△PBC与△ABC的面积之比是________.
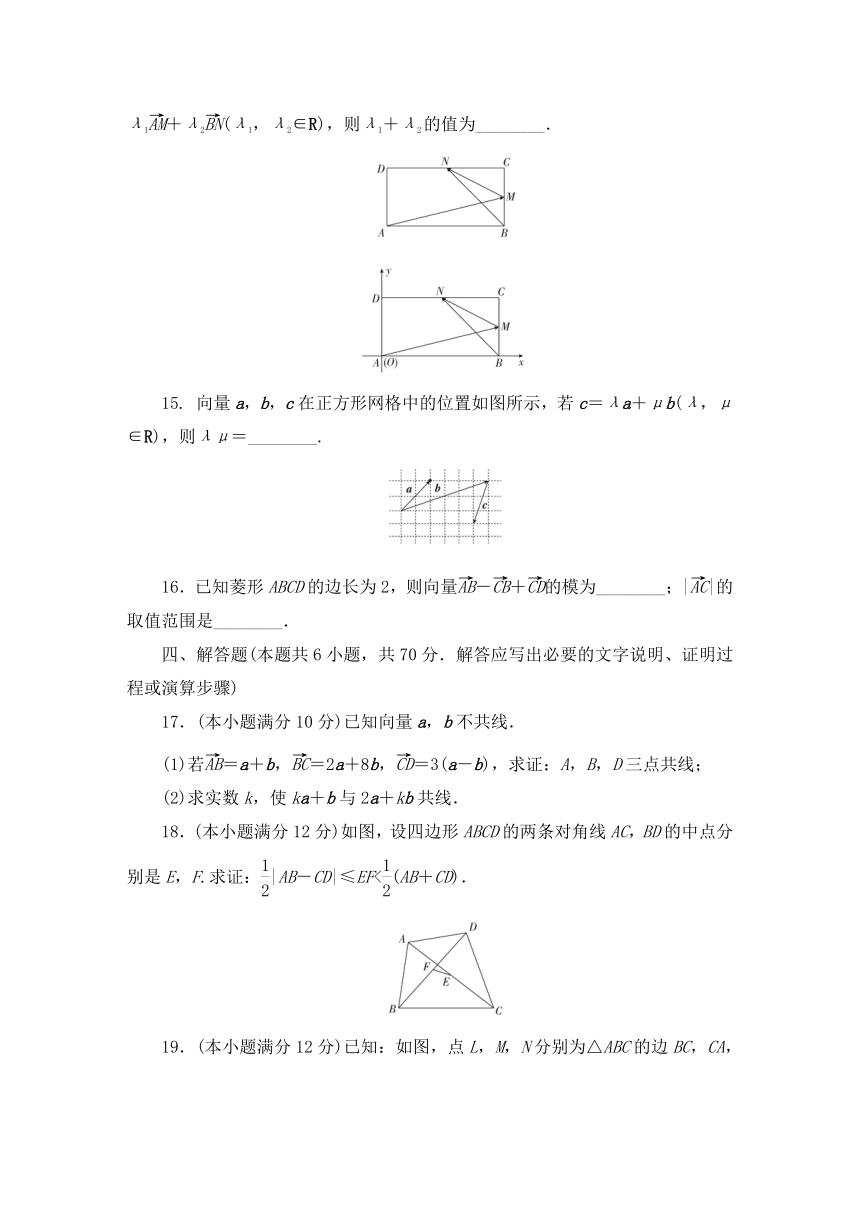
14.如图所示,在长方形ABCD中,M,N分别为线段BC,CD的中点,若=λ1+λ2(λ1,λ2∈R),则λ1+λ2的值为________.
15.
向量a,b,c在正方形网格中的位置如图所示,若c=λa+μb(λ,μ∈R),则λμ=________.
16.已知菱形ABCD的边长为2,则向量-+的模为________;||的取值范围是________.
四、解答题(本题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤)
17.(本小题满分10分)已知向量a,b不共线.
(1)若=a+b,=2a+8b,=3(a-b),求证:A,B,D三点共线;
(2)求实数k,使ka+b与2a+kb共线.
18.(本小题满分12分)如图,设四边形ABCD的两条对角线AC,BD的中点分别是E,F.求证:|AB-CD|≤EF<(AB+CD).
19.(本小题满分12分)已知:如图,点L,M,N分别为△ABC的边BC,CA,AB上的点,且=l,=m,=n,若++=0.
求证:l=m=n.
20.(本小题满分12分)已知四边形ABCD的顶点坐标为A(4,-1),B(3,4),D(1,-2),且=λ(λ>0).
(1)若点C在第一象限,求实数λ的取值范围;
(2)若点M为直线AC外一点,且=+,问实数λ为何值时,点P恰为四边形ABCD对角线的交点.
21.(本小题满分12分)已知点A(x,0),B(2x,1),C(2,x),D(6,2x).
(1)求实数x的值,使向量与共线;
(2)当向量与共线时,点A,B,C,D是否在一条直线上?
22.(本小题满分12分)如图所示,已知△ABC中,D,E,F分别是AC,AB,BC的中点,AF与CE相交于点O.
(1)求AO∶OF与CO∶OE的值;
(2)证明AF,BD,CE交于一点O.
第六章 单元质量测评
时间:120分钟 满分:150分
一、单项选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知点A(0,1),B(3,2),向量=(-4,-3),则向量=( )
A.(-7,-4)
B.(7,4)
C.(-1,4)
D.(1,4)
答案 A
解析 =-,=(-4,-3),=(3,1),故=(-7,-4).
2.如图所示,已知=3,=3,则向量与的关系为( )
A.共线
B.同向
C.共线且同向
D.共线、同向,且的长度是的3倍
答案 D
解析 由题意,知=+,=+=3+3=3,故选D.
3.已知向量a=(1,1),b=(2,x),若a+b与4b-2a平行,则实数x的值是( )
A.-2
B.0
C.1
D.2
答案 D
解析 因为a=(1,1),b=(2,x),所以a+b=(3,x+1),4b-2a=(6,4x-2),由于a+b与4b-2a平行,则6(x+1)-3(4x-2)=0,解得x=2.
4.已知三个力f1=(-2,-1),f2=(-3,2),f3=(4,-3)同时作用于某物体上一点,为使物体保持平衡,现加上一个力f4,则f4=( )
A.(-1,-2)
B.(1,-2)
C.(-1,2)
D.(1,2)
答案 D
解析 由题意知f4=-(f1+f2+f3)=-[(-2,-1)+(-3,2)+(4,-3)]=-(-1,-2)=(1,2).
5.已知平面内M,N,P三点满足-+=0,则下列说法正确的是( )
A.M,N,P是一个三角形的三个顶点
B.M,N,P是一条直线上的三个点
C.M,N,P是平面内的任意三个点
D.以上都不对
答案 C
解析 因为-+=++=+=0,所以-+=0对任意情况是恒成立的.故M,N,P是平面内的任意三个点.故选C.
6.已知△ABC中,点D在BC边上,且=2,=r+s,则r+s的值是( )
A.
B.
C.-3
D.0
答案 D
解析 如图,连接AD,∵=2,
∴=,又=-,∴=-,
∴=-,又=r+s,
∴r=,s=-,∴r+s=0.故选D.
7.在梯形ABCD中,AB∥CD,且DC=2AB,三个顶点A(1,2),B(2,1),C(4,2),则点D的坐标为( )
A.(2,4)
B.(2,2)
C.(4,1)
D.(4,4)
答案 A
解析 ∵在梯形ABCD中,DC=2AB,∴=2.
设点D的坐标为(x,y).∵=(4,2)-(x,y)=(4-x,2-y),=(2,1)-(1,2)=(1,-1),∴(4-x,2-y)=2(1,-1),即(4-x,2-y)=(2,-2),
∴解得故点D的坐标为(2,4).
8.在△ABC中,=,DE∥BC,且DE与AC相交于点E,M是BC的中点,AM与DE相交于点N.若=x+y(x,y∈R),则x+y=( )
A.1
B.
C.
D.
答案 C
解析 ∵=,∴AD=AB.∵DE∥BC,∴AE=AC.又M为BC的中点,∴N为DE的中点.∴=(+)==+,∴x=y=,∴x+y=+=.
二、多项选择题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分)
9.
如图,在梯形ABDC中,AB∥CD,||=2||,AD与BC相交于点O,则下列结论正确的是( )
A.-=
B.+++=0
C.|+2|=0
D.=+
答案 ABC
解析 对于A,-==,A正确;对于B,利用向量的线性运算可知,B正确;对于C,由于==,所以+2=0,故|+2|=0,C正确;对于D,==(+)=(+++)=(+2)=+,D错误.故选ABC.
10.如图2,“六芒星”是由两个全等正三角形组成,中心重合于点O且三组对边分别平行,点F,B是“六芒星”(如图1)的两个顶点,动点P在“六芒星”上(内部以及边界),若=x+y,则x+y的取值可能是( )
A.-6
B.1
C.5
D.9
答案 BC
解析 设=a,=b,求x+y的最大值,只需考虑如图中6个顶点的向量即可,讨论如下:
(1)∵=a,∴(x,y)=(1,0);
(2)∵=+=b+3a,∴(x,y)=(3,1);
(3)∵=+=b+2a,
∴(x,y)=(2,1);
(4)∵=++=b+a+(b+2a)=3a+2b,
∴(x,y)=(3,2);
(5)∵=+=b+a,∴(x,y)=(1,1);
(6)∵=b,∴(x,y)=(0,1),
∴x+y的最大值为3+2=5.
根据其对称性,可知x+y的最小值为-5.
故x+y的取值范围是[-5,5],
观察选项,B,C均符合题意.故选BC.
11.已知图中∠AOC+2∠BOC=180°,||=||,BC∥OA,P为图中的阴影中(含边界)任意点,并且=x+y,下列命题正确的是( )
A.0≤x+y≤1
B.|x|+|y|≤x2+y2
C.x2+y2≤2
D.存在无数个点P,使得y=1
答案 ACD
解析 当点P在OB上时,|x|=|y|,x+y=0,当点P在△OBC内时,|x|<|y|,x<0,0x2+y2,故B错误,对于D,如图,点P可以是线段BC上任意一点,都使y=1,故D正确.故选ACD.
12.定义平面向量之间的一种运算“⊙”如下:对任意的a=(m,n),b=(p,q),令a⊙b=mq-np,则下列说法正确的是( )
A.若a与b共线,则a⊙b=0
B.a⊙b=b⊙a
C.对任意的λ∈R,有(λa)⊙b=λ(a⊙b)
D.(a⊙b)2+(b⊙a)2=|a|2|b|2
答案 AC
解析 对于A,若a与b共线,则有a⊙b=mq-np=0,故A正确;对于B,因为b⊙a=pn-qm,而a⊙b=mq-np,所以有a⊙b≠b⊙a,故B错误;对于C,(λa)⊙b=λqm-λpn,而λ(a⊙b)=λ(qm-pn)=λqm-λpn,故C正确;对于D,(a⊙b)2+(b⊙a)2=(qm-pn)2+(pn-qm)2≠(m2+n2)(p2+q2)=|a|2|b|2,D错误.故选AC.
三、填空题(本题共4小题,每小题5分,共20分.把答案填在题中的横线上)
13.△ABC所在的平面内有一点P,满足+2+=2,则△PBC与△ABC的面积之比是________.
答案
解析 因为+2+=2,所以+2+=2-2,所以=-3=3,即P是AC边的一个四等分点,且PC=AC,由三角形的面积公式知,==.
14.如图所示,在长方形ABCD中,M,N分别为线段BC,CD的中点,若=λ1+λ2(λ1,λ2∈R),则λ1+λ2的值为________.
答案
解析 设AB=a,AD=b(a≠0,b≠0),以A为坐标原点,AB所在直线为x轴,AD所在直线为y轴,建立如图所示的平面直角坐标系,则A(0,0),B(a,0),C(a,b),D(0,b),M,N,则=,=,=,又=λ1+λ2(λ1,λ2∈R),即=λ1+λ2,则即解得所以λ1+λ2=.
15.
向量a,b,c在正方形网格中的位置如图所示,若c=λa+μb(λ,μ∈R),则λμ=________.
答案 -1
解析 以a,b的公共起点为原点建立平面直角坐标系如图,
则a=(2,2),b=(6,2),
c=(-1,-3).
∵c=λa+μb(λ,μ∈R),
即(-1,-3)=λ(2,2)+μ(6,2)=(2λ+6μ,2λ+2μ),
∴解得∴λμ=-1.
16.已知菱形ABCD的边长为2,则向量-+的模为________;||的取值范围是________.
答案 2 (0,4)
解析 因为-+=++=,
又||=2,所以|-+|=||=2.
又因为=+,且在菱形ABCD中,||=2,
所以|||-|||<||=|+|<||+|A|,即0<||<4.
四、解答题(本题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤)
17.(本小题满分10分)已知向量a,b不共线.
(1)若=a+b,=2a+8b,=3(a-b),求证:A,B,D三点共线;
(2)求实数k,使ka+b与2a+kb共线.
解 (1)证明:=a+b,=++=6a+6b,显然=.
故∥,又与有公共点A,
故A,B,D三点共线.
(2)若ka+b∥2a+kb,必存在实数λ,使得ka+b=λ(2a+kb),整理得ka+b=2λa+λkb,
又a与b不共线,故得=即k=±.
当k=时,ka+b=a+b,2a+kb=2a+b,
此时ka+b∥2a+kb,
同理可验证k=-时亦符合题意.
故k=±.
18.(本小题满分12分)如图,设四边形ABCD的两条对角线AC,BD的中点分别是E,F.求证:|AB-CD|≤EF<(AB+CD).
证明 ∵=++,=++,
∴2=(+)+(+)+(+).
∵E,F分别是AC,BD的中点,
∴+=0,+=0,∴=(+).
∵|||-|||≤|+|<||+||,
∴|||-|||≤||<(||+||),
即|AB-CD|≤EF<(AB+CD).
19.(本小题满分12分)已知:如图,点L,M,N分别为△ABC的边BC,CA,AB上的点,且=l,=m,=n,若++=0.
求证:l=m=n.
证明 设=a,=b为基底.
由已知得=la,=mb,
∵=+=-a-b,
∴=n=-na-nb,
∴=+=(l-1)a-b,①
=+=a+mb,②
=+=-na+(1-n)b,③
将①②③代入++=0,得(l-n)a+(m-n)b=0,∵a,b不共线,∴l-n=0,m-n=0,即l=m=n.
20.(本小题满分12分)已知四边形ABCD的顶点坐标为A(4,-1),B(3,4),D(1,-2),且=λ(λ>0).
(1)若点C在第一象限,求实数λ的取值范围;
(2)若点M为直线AC外一点,且=+,问实数λ为何值时,点P恰为四边形ABCD对角线的交点.
解 (1)因为A(4,-1),B(3,4),所以=(-1,5),
设点C的坐标为(x,y),则=(x-1,y+2),
而=λ(λ>0),所以
解得
因为点C在第一象限,所以1<λ<.
(2)由=+得
2(-)=3(-),
即2=3,若点P恰为四边形ABCD对角线的交点且=λ(λ>0),则=λ,所以λ=.
21.(本小题满分12分)已知点A(x,0),B(2x,1),C(2,x),D(6,2x).
(1)求实数x的值,使向量与共线;
(2)当向量与共线时,点A,B,C,D是否在一条直线上?
解 (1)=(2x,1)-(x,0)=(x,1),
=(6,2x)-(2,x)=(4,x).
若向量与共线,则x2-4×1=0,故x=±2.
∴当x=±2时,向量与共线.
(2)当x=2时,A(2,0),B(4,1),C(2,2),=(4,1)-(2,0)=(2,1),=(2,2)-(2,0)=(0,2).
∵2×2-0×1≠0,∴向量与不共线,
∴点A,B,C不在一条直线上,
∴点A,B,C,D不在一条直线上.
当x=-2时,A(-2,0),B(-4,1),C(2,-2),
=(-4,1)-(-2,0)=(-2,1),
=(2,-2)-(-2,0)=(4,-2).
∵(-2)×(-2)-4×1=0,
∴向量与共线,
∵AB与AC有公共点A,
∴点A,B,C在一条直线上.
又向量与共线,∴AB与CD平行或重合.
又A,B,C在一条直线上,
∴点A,B,C,D在一条直线上.
综上,当x=2时,向量与共线,但点A,B,C,D不在一条直线上.
当x=-2时,向量与共线,且点A,B,C,D在一条直线上.
22.(本小题满分12分)如图所示,已知△ABC中,D,E,F分别是AC,AB,BC的中点,AF与CE相交于点O.
(1)求AO∶OF与CO∶OE的值;
(2)证明AF,BD,CE交于一点O.
解 (1)因为=+=+,又因为E,F都是中点,所以+=+=2+2=2.
另外,=+,所以+=2+2.
设=s,=t,
则有s-t=2+2,
即(s-2)=(t-2).
从而由共线向量基本定理可知s=t=2,
因此AO∶OF=CO∶OE=2∶1.
(2)证明:要证明AF,BD,CE交于一点O,只需证明B,O,D三点共线即可.
由(1)可知,=+,
=+=+=-
=-=(+),
又=(+),所以∥,又与有公共点B,
所以B,O,D三点共线,故AF,BD,CE交于一点.
时间:120分钟 满分:150分
一、单项选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知点A(0,1),B(3,2),向量=(-4,-3),则向量=( )
A.(-7,-4)
B.(7,4)
C.(-1,4)
D.(1,4)
2.如图所示,已知=3,=3,则向量与的关系为( )
A.共线
B.同向
C.共线且同向
D.共线、同向,且的长度是的3倍
3.已知向量a=(1,1),b=(2,x),若a+b与4b-2a平行,则实数x的值是( )
A.-2
B.0
C.1
D.2
4.已知三个力f1=(-2,-1),f2=(-3,2),f3=(4,-3)同时作用于某物体上一点,为使物体保持平衡,现加上一个力f4,则f4=( )
A.(-1,-2)
B.(1,-2)
C.(-1,2)
D.(1,2)
5.已知平面内M,N,P三点满足-+=0,则下列说法正确的是( )
A.M,N,P是一个三角形的三个顶点
B.M,N,P是一条直线上的三个点
C.M,N,P是平面内的任意三个点
D.以上都不对
6.已知△ABC中,点D在BC边上,且=2,=r+s,则r+s的值是( )
A.
B.
C.-3
D.0
7.在梯形ABCD中,AB∥CD,且DC=2AB,三个顶点A(1,2),B(2,1),C(4,2),则点D的坐标为( )
A.(2,4)
B.(2,2)
C.(4,1)
D.(4,4)
8.在△ABC中,=,DE∥BC,且DE与AC相交于点E,M是BC的中点,AM与DE相交于点N.若=x+y(x,y∈R),则x+y=( )
A.1
B.
C.
D.
二、多项选择题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分)
9.
如图,在梯形ABDC中,AB∥CD,||=2||,AD与BC相交于点O,则下列结论正确的是( )
A.-=
B.+++=0
C.|+2|=0
D.=+
10.如图2,“六芒星”是由两个全等正三角形组成,中心重合于点O且三组对边分别平行,点F,B是“六芒星”(如图1)的两个顶点,动点P在“六芒星”上(内部以及边界),若=x+y,则x+y的取值可能是( )
A.-6
B.1
C.5
D.9
11.已知图中∠AOC+2∠BOC=180°,||=||,BC∥OA,P为图中的阴影中(含边界)任意点,并且=x+y,下列命题正确的是( )
A.0≤x+y≤1
B.|x|+|y|≤x2+y2
C.x2+y2≤2
D.存在无数个点P,使得y=1
12.定义平面向量之间的一种运算“⊙”如下:对任意的a=(m,n),b=(p,q),令a⊙b=mq-np,则下列说法正确的是( )
A.若a与b共线,则a⊙b=0
B.a⊙b=b⊙a
C.对任意的λ∈R,有(λa)⊙b=λ(a⊙b)
D.(a⊙b)2+(b⊙a)2=|a|2|b|2
三、填空题(本题共4小题,每小题5分,共20分.把答案填在题中的横线上)
13.△ABC所在的平面内有一点P,满足+2+=2,则△PBC与△ABC的面积之比是________.
14.如图所示,在长方形ABCD中,M,N分别为线段BC,CD的中点,若=λ1+λ2(λ1,λ2∈R),则λ1+λ2的值为________.
15.
向量a,b,c在正方形网格中的位置如图所示,若c=λa+μb(λ,μ∈R),则λμ=________.
16.已知菱形ABCD的边长为2,则向量-+的模为________;||的取值范围是________.
四、解答题(本题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤)
17.(本小题满分10分)已知向量a,b不共线.
(1)若=a+b,=2a+8b,=3(a-b),求证:A,B,D三点共线;
(2)求实数k,使ka+b与2a+kb共线.
18.(本小题满分12分)如图,设四边形ABCD的两条对角线AC,BD的中点分别是E,F.求证:|AB-CD|≤EF<(AB+CD).
19.(本小题满分12分)已知:如图,点L,M,N分别为△ABC的边BC,CA,AB上的点,且=l,=m,=n,若++=0.
求证:l=m=n.
20.(本小题满分12分)已知四边形ABCD的顶点坐标为A(4,-1),B(3,4),D(1,-2),且=λ(λ>0).
(1)若点C在第一象限,求实数λ的取值范围;
(2)若点M为直线AC外一点,且=+,问实数λ为何值时,点P恰为四边形ABCD对角线的交点.
21.(本小题满分12分)已知点A(x,0),B(2x,1),C(2,x),D(6,2x).
(1)求实数x的值,使向量与共线;
(2)当向量与共线时,点A,B,C,D是否在一条直线上?
22.(本小题满分12分)如图所示,已知△ABC中,D,E,F分别是AC,AB,BC的中点,AF与CE相交于点O.
(1)求AO∶OF与CO∶OE的值;
(2)证明AF,BD,CE交于一点O.
第六章 单元质量测评
时间:120分钟 满分:150分
一、单项选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知点A(0,1),B(3,2),向量=(-4,-3),则向量=( )
A.(-7,-4)
B.(7,4)
C.(-1,4)
D.(1,4)
答案 A
解析 =-,=(-4,-3),=(3,1),故=(-7,-4).
2.如图所示,已知=3,=3,则向量与的关系为( )
A.共线
B.同向
C.共线且同向
D.共线、同向,且的长度是的3倍
答案 D
解析 由题意,知=+,=+=3+3=3,故选D.
3.已知向量a=(1,1),b=(2,x),若a+b与4b-2a平行,则实数x的值是( )
A.-2
B.0
C.1
D.2
答案 D
解析 因为a=(1,1),b=(2,x),所以a+b=(3,x+1),4b-2a=(6,4x-2),由于a+b与4b-2a平行,则6(x+1)-3(4x-2)=0,解得x=2.
4.已知三个力f1=(-2,-1),f2=(-3,2),f3=(4,-3)同时作用于某物体上一点,为使物体保持平衡,现加上一个力f4,则f4=( )
A.(-1,-2)
B.(1,-2)
C.(-1,2)
D.(1,2)
答案 D
解析 由题意知f4=-(f1+f2+f3)=-[(-2,-1)+(-3,2)+(4,-3)]=-(-1,-2)=(1,2).
5.已知平面内M,N,P三点满足-+=0,则下列说法正确的是( )
A.M,N,P是一个三角形的三个顶点
B.M,N,P是一条直线上的三个点
C.M,N,P是平面内的任意三个点
D.以上都不对
答案 C
解析 因为-+=++=+=0,所以-+=0对任意情况是恒成立的.故M,N,P是平面内的任意三个点.故选C.
6.已知△ABC中,点D在BC边上,且=2,=r+s,则r+s的值是( )
A.
B.
C.-3
D.0
答案 D
解析 如图,连接AD,∵=2,
∴=,又=-,∴=-,
∴=-,又=r+s,
∴r=,s=-,∴r+s=0.故选D.
7.在梯形ABCD中,AB∥CD,且DC=2AB,三个顶点A(1,2),B(2,1),C(4,2),则点D的坐标为( )
A.(2,4)
B.(2,2)
C.(4,1)
D.(4,4)
答案 A
解析 ∵在梯形ABCD中,DC=2AB,∴=2.
设点D的坐标为(x,y).∵=(4,2)-(x,y)=(4-x,2-y),=(2,1)-(1,2)=(1,-1),∴(4-x,2-y)=2(1,-1),即(4-x,2-y)=(2,-2),
∴解得故点D的坐标为(2,4).
8.在△ABC中,=,DE∥BC,且DE与AC相交于点E,M是BC的中点,AM与DE相交于点N.若=x+y(x,y∈R),则x+y=( )
A.1
B.
C.
D.
答案 C
解析 ∵=,∴AD=AB.∵DE∥BC,∴AE=AC.又M为BC的中点,∴N为DE的中点.∴=(+)==+,∴x=y=,∴x+y=+=.
二、多项选择题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得3分,有选错的得0分)
9.
如图,在梯形ABDC中,AB∥CD,||=2||,AD与BC相交于点O,则下列结论正确的是( )
A.-=
B.+++=0
C.|+2|=0
D.=+
答案 ABC
解析 对于A,-==,A正确;对于B,利用向量的线性运算可知,B正确;对于C,由于==,所以+2=0,故|+2|=0,C正确;对于D,==(+)=(+++)=(+2)=+,D错误.故选ABC.
10.如图2,“六芒星”是由两个全等正三角形组成,中心重合于点O且三组对边分别平行,点F,B是“六芒星”(如图1)的两个顶点,动点P在“六芒星”上(内部以及边界),若=x+y,则x+y的取值可能是( )
A.-6
B.1
C.5
D.9
答案 BC
解析 设=a,=b,求x+y的最大值,只需考虑如图中6个顶点的向量即可,讨论如下:
(1)∵=a,∴(x,y)=(1,0);
(2)∵=+=b+3a,∴(x,y)=(3,1);
(3)∵=+=b+2a,
∴(x,y)=(2,1);
(4)∵=++=b+a+(b+2a)=3a+2b,
∴(x,y)=(3,2);
(5)∵=+=b+a,∴(x,y)=(1,1);
(6)∵=b,∴(x,y)=(0,1),
∴x+y的最大值为3+2=5.
根据其对称性,可知x+y的最小值为-5.
故x+y的取值范围是[-5,5],
观察选项,B,C均符合题意.故选BC.
11.已知图中∠AOC+2∠BOC=180°,||=||,BC∥OA,P为图中的阴影中(含边界)任意点,并且=x+y,下列命题正确的是( )
A.0≤x+y≤1
B.|x|+|y|≤x2+y2
C.x2+y2≤2
D.存在无数个点P,使得y=1
答案 ACD
解析 当点P在OB上时,|x|=|y|,x+y=0,当点P在△OBC内时,|x|<|y|,x<0,0
12.定义平面向量之间的一种运算“⊙”如下:对任意的a=(m,n),b=(p,q),令a⊙b=mq-np,则下列说法正确的是( )
A.若a与b共线,则a⊙b=0
B.a⊙b=b⊙a
C.对任意的λ∈R,有(λa)⊙b=λ(a⊙b)
D.(a⊙b)2+(b⊙a)2=|a|2|b|2
答案 AC
解析 对于A,若a与b共线,则有a⊙b=mq-np=0,故A正确;对于B,因为b⊙a=pn-qm,而a⊙b=mq-np,所以有a⊙b≠b⊙a,故B错误;对于C,(λa)⊙b=λqm-λpn,而λ(a⊙b)=λ(qm-pn)=λqm-λpn,故C正确;对于D,(a⊙b)2+(b⊙a)2=(qm-pn)2+(pn-qm)2≠(m2+n2)(p2+q2)=|a|2|b|2,D错误.故选AC.
三、填空题(本题共4小题,每小题5分,共20分.把答案填在题中的横线上)
13.△ABC所在的平面内有一点P,满足+2+=2,则△PBC与△ABC的面积之比是________.
答案
解析 因为+2+=2,所以+2+=2-2,所以=-3=3,即P是AC边的一个四等分点,且PC=AC,由三角形的面积公式知,==.
14.如图所示,在长方形ABCD中,M,N分别为线段BC,CD的中点,若=λ1+λ2(λ1,λ2∈R),则λ1+λ2的值为________.
答案
解析 设AB=a,AD=b(a≠0,b≠0),以A为坐标原点,AB所在直线为x轴,AD所在直线为y轴,建立如图所示的平面直角坐标系,则A(0,0),B(a,0),C(a,b),D(0,b),M,N,则=,=,=,又=λ1+λ2(λ1,λ2∈R),即=λ1+λ2,则即解得所以λ1+λ2=.
15.
向量a,b,c在正方形网格中的位置如图所示,若c=λa+μb(λ,μ∈R),则λμ=________.
答案 -1
解析 以a,b的公共起点为原点建立平面直角坐标系如图,
则a=(2,2),b=(6,2),
c=(-1,-3).
∵c=λa+μb(λ,μ∈R),
即(-1,-3)=λ(2,2)+μ(6,2)=(2λ+6μ,2λ+2μ),
∴解得∴λμ=-1.
16.已知菱形ABCD的边长为2,则向量-+的模为________;||的取值范围是________.
答案 2 (0,4)
解析 因为-+=++=,
又||=2,所以|-+|=||=2.
又因为=+,且在菱形ABCD中,||=2,
所以|||-|||<||=|+|<||+|A|,即0<||<4.
四、解答题(本题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤)
17.(本小题满分10分)已知向量a,b不共线.
(1)若=a+b,=2a+8b,=3(a-b),求证:A,B,D三点共线;
(2)求实数k,使ka+b与2a+kb共线.
解 (1)证明:=a+b,=++=6a+6b,显然=.
故∥,又与有公共点A,
故A,B,D三点共线.
(2)若ka+b∥2a+kb,必存在实数λ,使得ka+b=λ(2a+kb),整理得ka+b=2λa+λkb,
又a与b不共线,故得=即k=±.
当k=时,ka+b=a+b,2a+kb=2a+b,
此时ka+b∥2a+kb,
同理可验证k=-时亦符合题意.
故k=±.
18.(本小题满分12分)如图,设四边形ABCD的两条对角线AC,BD的中点分别是E,F.求证:|AB-CD|≤EF<(AB+CD).
证明 ∵=++,=++,
∴2=(+)+(+)+(+).
∵E,F分别是AC,BD的中点,
∴+=0,+=0,∴=(+).
∵|||-|||≤|+|<||+||,
∴|||-|||≤||<(||+||),
即|AB-CD|≤EF<(AB+CD).
19.(本小题满分12分)已知:如图,点L,M,N分别为△ABC的边BC,CA,AB上的点,且=l,=m,=n,若++=0.
求证:l=m=n.
证明 设=a,=b为基底.
由已知得=la,=mb,
∵=+=-a-b,
∴=n=-na-nb,
∴=+=(l-1)a-b,①
=+=a+mb,②
=+=-na+(1-n)b,③
将①②③代入++=0,得(l-n)a+(m-n)b=0,∵a,b不共线,∴l-n=0,m-n=0,即l=m=n.
20.(本小题满分12分)已知四边形ABCD的顶点坐标为A(4,-1),B(3,4),D(1,-2),且=λ(λ>0).
(1)若点C在第一象限,求实数λ的取值范围;
(2)若点M为直线AC外一点,且=+,问实数λ为何值时,点P恰为四边形ABCD对角线的交点.
解 (1)因为A(4,-1),B(3,4),所以=(-1,5),
设点C的坐标为(x,y),则=(x-1,y+2),
而=λ(λ>0),所以
解得
因为点C在第一象限,所以1<λ<.
(2)由=+得
2(-)=3(-),
即2=3,若点P恰为四边形ABCD对角线的交点且=λ(λ>0),则=λ,所以λ=.
21.(本小题满分12分)已知点A(x,0),B(2x,1),C(2,x),D(6,2x).
(1)求实数x的值,使向量与共线;
(2)当向量与共线时,点A,B,C,D是否在一条直线上?
解 (1)=(2x,1)-(x,0)=(x,1),
=(6,2x)-(2,x)=(4,x).
若向量与共线,则x2-4×1=0,故x=±2.
∴当x=±2时,向量与共线.
(2)当x=2时,A(2,0),B(4,1),C(2,2),=(4,1)-(2,0)=(2,1),=(2,2)-(2,0)=(0,2).
∵2×2-0×1≠0,∴向量与不共线,
∴点A,B,C不在一条直线上,
∴点A,B,C,D不在一条直线上.
当x=-2时,A(-2,0),B(-4,1),C(2,-2),
=(-4,1)-(-2,0)=(-2,1),
=(2,-2)-(-2,0)=(4,-2).
∵(-2)×(-2)-4×1=0,
∴向量与共线,
∵AB与AC有公共点A,
∴点A,B,C在一条直线上.
又向量与共线,∴AB与CD平行或重合.
又A,B,C在一条直线上,
∴点A,B,C,D在一条直线上.
综上,当x=2时,向量与共线,但点A,B,C,D不在一条直线上.
当x=-2时,向量与共线,且点A,B,C,D在一条直线上.
22.(本小题满分12分)如图所示,已知△ABC中,D,E,F分别是AC,AB,BC的中点,AF与CE相交于点O.
(1)求AO∶OF与CO∶OE的值;
(2)证明AF,BD,CE交于一点O.
解 (1)因为=+=+,又因为E,F都是中点,所以+=+=2+2=2.
另外,=+,所以+=2+2.
设=s,=t,
则有s-t=2+2,
即(s-2)=(t-2).
从而由共线向量基本定理可知s=t=2,
因此AO∶OF=CO∶OE=2∶1.
(2)证明:要证明AF,BD,CE交于一点O,只需证明B,O,D三点共线即可.
由(1)可知,=+,
=+=+=-
=-=(+),
又=(+),所以∥,又与有公共点B,
所以B,O,D三点共线,故AF,BD,CE交于一点.
