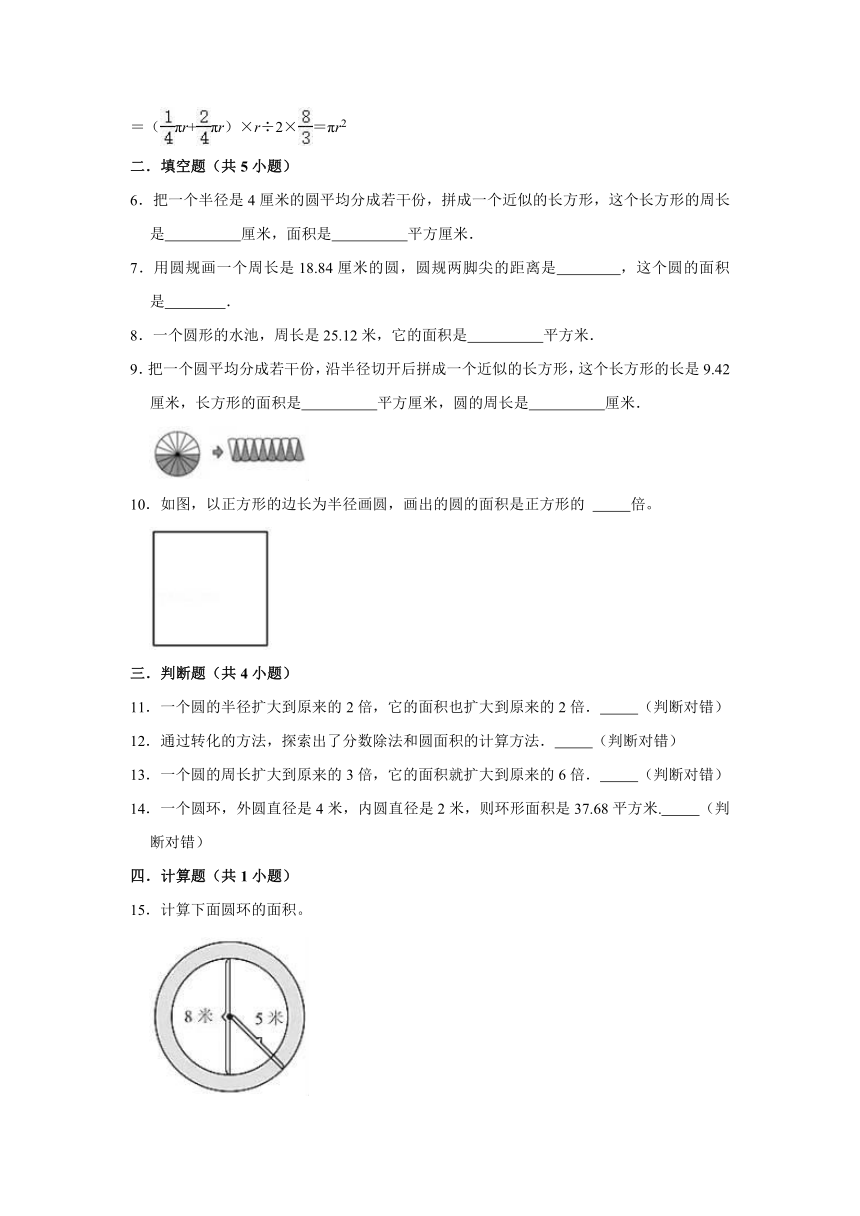
2021-2022学年人教版六年级数学上册《5.3 圆的面积》同步练习(含答案)
文档属性
| 名称 | 2021-2022学年人教版六年级数学上册《5.3 圆的面积》同步练习(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 112.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-23 00:00:00 | ||
图片预览



文档简介
2021-2022学年人教版六年级数学上册《5.3
圆的面积》同步练习
一.选择题(共5小题)
1.钟面上时针的长度1分米,一昼夜时针扫过的面积( )平方分米.
A.2π
B.12π
C.24π
D.48π
2.在解决下面四个问题时,都运用了( )策略。
a.如图①方式,推导三角形面积公式的过程。
b.如图②方式,推导圆面积公式的过程。
c.计算1.2×3.6时,先看成12×36,再在积中添上小数点。
d.计算12÷时,可以这样算12÷=12×。
A.画图
B.替换
C.倒推
D.转化
3.在一张长为8厘米、宽为6厘米的长方形纸片上剪一个尽可能大的圆形,剪出的圆形纸片的面积是( )平方厘米。
A.25.12
B.28.26
C.50.24
D.200.96
4.一个圆的半径扩大为原来的3倍,面积就扩大为原来的( )
A.3倍
B.9倍
C.6倍
D.9.42倍
5.下面是1名同学推导圆面积公式的过程,其中错误的是( )
A.长=πr,宽=rS圆=长×宽=πr×r=πr2
B.底=πr,高=rS圆=底×高=πr×r=πr2
C.底=πr,高=rS圆=底×高÷2×8=πr×r×8=πr2
D.上底+下底=(πr+πr),高=rS圆=(上底+下底)×高÷2×=(πr+πr)×r÷2×=πr2
二.填空题(共5小题)
6.把一个半径是4厘米的圆平均分成若干份,拼成一个近似的长方形,这个长方形的周长是
厘米,面积是
平方厘米.
7.用圆规画一个周长是18.84厘米的圆,圆规两脚尖的距离是
,这个圆的面积是
.
8.一个圆形的水池,周长是25.12米,它的面积是
平方米.
9.把一个圆平均分成若干份,沿半径切开后拼成一个近似的长方形,这个长方形的长是9.42厘米,长方形的面积是
平方厘米,圆的周长是
厘米.
10.如图,以正方形的边长为半径画圆,画出的圆的面积是正方形的
倍。
三.判断题(共4小题)
11.一个圆的半径扩大到原来的2倍,它的面积也扩大到原来的2倍.
(判断对错)
12.通过转化的方法,探索出了分数除法和圆面积的计算方法.
(判断对错)
13.一个圆的周长扩大到原来的3倍,它的面积就扩大到原来的6倍.
(判断对错)
14.一个圆环,外圆直径是4米,内圆直径是2米,则环形面积是37.68平方米.
(判断对错)
四.计算题(共1小题)
15.计算下面圆环的面积。
五.应用题(共6小题)
16.有一个半环形的橡胶垫圈,如图所示(单位:厘米).把它平放在桌子上,所占面积是多少?
17.一个圆形花坛的面积为314平方米.绕这个花坛走一圈,有多少米?
18.实践周期间小亮和小明测量了学校的圆形花坛.
19.一块正方形铁板,在上面画一个最大的圆,已知圆的周长是18.84分米.这块铁板的面积是多少平方分米?
20.在一个直径10米的圆形水池的周围铺上一条3米宽的石子小路,这条小路的面积是多少平方米?
21.将一个圆剪拼成一个近似的平行四边形(如图),周长增加了10cm.原来圆的周长是多少?面积呢?
参考答案与试题解析
一.选择题(共5小题)
1.解:π×12×2=2π(平方分米),
答:一昼夜时针扫过的面积是2π平方分米.
故选:A.
2.解:a.如图①方式,推导三角形面积公式的过程,把三角形面积转化成平行四边形面积;
b.如图②方式,推导圆面积公式的过程,把圆的面积转化成长方形面积;
c.计算1.2×3.6时,先看成12×36,再在积中添上小数点,把小数乘法转化成整数乘法;
d.计算12÷时,可以这样算12÷=12×,把除法转化为乘法;
以上四个问题,都运用了转化的策略。
故选:D。
3.解:6÷2=3(厘米)
3.14×3×3=28.26(平方厘米)
答:剪出的圆形纸片的面积是28.26平方厘米。
故选:B。
4.解:3×3=9
答:一个圆的半径扩大为原来的3倍,面积就扩大为原来的9倍。
故选:B。
5.解:A、B、D这三种方法都是正确的.
C的推导过程是错误的,错误的原因是每个近似三角形的底=2πr,高=r,而不是底=πr。
故选:C。
二.填空题(共5小题)
6.解:(1)3.14×4×2+4×2
=3.14×8+8
=25.12+8
=33.12(厘米)
(2)3.14×42
=3.14×16
=50.24(平方厘米)
答:这个长方形的面积是50.24平方厘米,周长是33.12厘米;
故答案为:33.12;50.24.
7.解:圆的半径:18.84÷(2×3.14)
=18.84÷6.28
=3(厘米);
圆的面积:3.14×32=28.28(平方厘米);
答:圆规两脚尖的距离为3厘米,这个圆的面积是28.26平方厘米.
故答案为:3厘米;28.26平方厘米.
8.解:3.14×(25.12÷3.14÷2)2,
=3.14×42,
=3.14×16,
=50.24(平方米).
答:这个水池的面积是50.24平方米.
故答案为:50.24.
9.解:9.42÷3.14=3(厘米)
9.42×3=28.26(平方厘米)
2×3.14×3=18.84(厘米)
答:长方形的面积是28.26平方厘米,圆的周长是18.84厘米.
故答案为:28.26、18.84.
10.解:设正方形的边长为a,
方形的面积=a2
圆的面积=π×a2
(π×a2)÷a2=π
答:画出的圆的面积是正方形的π倍。
故答案为:π。
三.判断题(共4小题)
11.解:一个圆的半径扩大到原来的2倍,面积扩大到原来的2×2=4倍,
所以题干的说法是错误的.
故答案为:×.
12.解:“转化”是小学阶段研究平面图形面积的计算方法常用的思想方法,如:探索平行四边形面积的计算方法、圆面积的计算方法等都是通过转化得来的;另外,在学习了倒数之后,探索分数除法的计算方法,也是通过转化,除以一个不为0的数,转化为乘这个数的倒数.
因此,通过转化的方法,探索出了分数除法和圆面积的计算方法.此说法是正确的.
故答案为:√.
13.解:根据分析可得,
当一个圆的周长扩大到原来的3倍,圆的半径扩大3倍,面积扩大32=9倍;所以原题说法错误.
故答案为:×.
14.解:3.14×[(4÷2)2﹣(2÷2)2]
=3.14×[4﹣1]
=3.14×3
=9.42(平方米)
答:这个环形的面积是9.42平方米。
9.42≠37.68
故答案为:×。
四.计算题(共1小题)
15.解:8÷2=4(米)
3.14×(52﹣42)
=3.14×(25﹣16)
=3.14×9
=28.26(平方米)
答:圆环的面积是28.26平方米。
五.应用题(共6小题)
16.解:3.14×(6÷2+1)2﹣3.14×(6÷2)2
=3.14×42﹣3.14×32
=3.14×(16﹣9)
=3.14×7
=21.98(平方厘米)
21.98÷2=10.99(平方厘米)
答:把它平放在桌子上,所占面积是10.99平方厘米.
17.解:314÷3.14=100(平方米)
因为10×10=100
所以圆的半径是10米,
3.14×10×2
=31.4×2
=62.8(米)
答:绕这个花坛走一圈,有62.8米.
18.解:25.12÷3.14÷2
=8÷2
=4(米);
3.14×42
=3.14×16
=50.24(平方米)
答:它的面积是50.24平方米.
19.解:18.84÷3.14=6(分米)
6×6=36(平方分米)
答:这块铁板的面积是36平方分米.
20.解:3.14×(10÷2+3)2﹣3.14×(10÷2)2
=3.14×64﹣3.14×25
=3.14×(64﹣25)
=122.46(平方米).
答:这条小路的面积是122.46平方米.
21.解:10÷2=5(厘米)
3.14×5×2=31.4(厘米)
3.14×52
=3.14×25
=78.5(平方厘米)
答:这个圆的周长是31.4厘米,面积是78.5平方厘米.
圆的面积》同步练习
一.选择题(共5小题)
1.钟面上时针的长度1分米,一昼夜时针扫过的面积( )平方分米.
A.2π
B.12π
C.24π
D.48π
2.在解决下面四个问题时,都运用了( )策略。
a.如图①方式,推导三角形面积公式的过程。
b.如图②方式,推导圆面积公式的过程。
c.计算1.2×3.6时,先看成12×36,再在积中添上小数点。
d.计算12÷时,可以这样算12÷=12×。
A.画图
B.替换
C.倒推
D.转化
3.在一张长为8厘米、宽为6厘米的长方形纸片上剪一个尽可能大的圆形,剪出的圆形纸片的面积是( )平方厘米。
A.25.12
B.28.26
C.50.24
D.200.96
4.一个圆的半径扩大为原来的3倍,面积就扩大为原来的( )
A.3倍
B.9倍
C.6倍
D.9.42倍
5.下面是1名同学推导圆面积公式的过程,其中错误的是( )
A.长=πr,宽=rS圆=长×宽=πr×r=πr2
B.底=πr,高=rS圆=底×高=πr×r=πr2
C.底=πr,高=rS圆=底×高÷2×8=πr×r×8=πr2
D.上底+下底=(πr+πr),高=rS圆=(上底+下底)×高÷2×=(πr+πr)×r÷2×=πr2
二.填空题(共5小题)
6.把一个半径是4厘米的圆平均分成若干份,拼成一个近似的长方形,这个长方形的周长是
厘米,面积是
平方厘米.
7.用圆规画一个周长是18.84厘米的圆,圆规两脚尖的距离是
,这个圆的面积是
.
8.一个圆形的水池,周长是25.12米,它的面积是
平方米.
9.把一个圆平均分成若干份,沿半径切开后拼成一个近似的长方形,这个长方形的长是9.42厘米,长方形的面积是
平方厘米,圆的周长是
厘米.
10.如图,以正方形的边长为半径画圆,画出的圆的面积是正方形的
倍。
三.判断题(共4小题)
11.一个圆的半径扩大到原来的2倍,它的面积也扩大到原来的2倍.
(判断对错)
12.通过转化的方法,探索出了分数除法和圆面积的计算方法.
(判断对错)
13.一个圆的周长扩大到原来的3倍,它的面积就扩大到原来的6倍.
(判断对错)
14.一个圆环,外圆直径是4米,内圆直径是2米,则环形面积是37.68平方米.
(判断对错)
四.计算题(共1小题)
15.计算下面圆环的面积。
五.应用题(共6小题)
16.有一个半环形的橡胶垫圈,如图所示(单位:厘米).把它平放在桌子上,所占面积是多少?
17.一个圆形花坛的面积为314平方米.绕这个花坛走一圈,有多少米?
18.实践周期间小亮和小明测量了学校的圆形花坛.
19.一块正方形铁板,在上面画一个最大的圆,已知圆的周长是18.84分米.这块铁板的面积是多少平方分米?
20.在一个直径10米的圆形水池的周围铺上一条3米宽的石子小路,这条小路的面积是多少平方米?
21.将一个圆剪拼成一个近似的平行四边形(如图),周长增加了10cm.原来圆的周长是多少?面积呢?
参考答案与试题解析
一.选择题(共5小题)
1.解:π×12×2=2π(平方分米),
答:一昼夜时针扫过的面积是2π平方分米.
故选:A.
2.解:a.如图①方式,推导三角形面积公式的过程,把三角形面积转化成平行四边形面积;
b.如图②方式,推导圆面积公式的过程,把圆的面积转化成长方形面积;
c.计算1.2×3.6时,先看成12×36,再在积中添上小数点,把小数乘法转化成整数乘法;
d.计算12÷时,可以这样算12÷=12×,把除法转化为乘法;
以上四个问题,都运用了转化的策略。
故选:D。
3.解:6÷2=3(厘米)
3.14×3×3=28.26(平方厘米)
答:剪出的圆形纸片的面积是28.26平方厘米。
故选:B。
4.解:3×3=9
答:一个圆的半径扩大为原来的3倍,面积就扩大为原来的9倍。
故选:B。
5.解:A、B、D这三种方法都是正确的.
C的推导过程是错误的,错误的原因是每个近似三角形的底=2πr,高=r,而不是底=πr。
故选:C。
二.填空题(共5小题)
6.解:(1)3.14×4×2+4×2
=3.14×8+8
=25.12+8
=33.12(厘米)
(2)3.14×42
=3.14×16
=50.24(平方厘米)
答:这个长方形的面积是50.24平方厘米,周长是33.12厘米;
故答案为:33.12;50.24.
7.解:圆的半径:18.84÷(2×3.14)
=18.84÷6.28
=3(厘米);
圆的面积:3.14×32=28.28(平方厘米);
答:圆规两脚尖的距离为3厘米,这个圆的面积是28.26平方厘米.
故答案为:3厘米;28.26平方厘米.
8.解:3.14×(25.12÷3.14÷2)2,
=3.14×42,
=3.14×16,
=50.24(平方米).
答:这个水池的面积是50.24平方米.
故答案为:50.24.
9.解:9.42÷3.14=3(厘米)
9.42×3=28.26(平方厘米)
2×3.14×3=18.84(厘米)
答:长方形的面积是28.26平方厘米,圆的周长是18.84厘米.
故答案为:28.26、18.84.
10.解:设正方形的边长为a,
方形的面积=a2
圆的面积=π×a2
(π×a2)÷a2=π
答:画出的圆的面积是正方形的π倍。
故答案为:π。
三.判断题(共4小题)
11.解:一个圆的半径扩大到原来的2倍,面积扩大到原来的2×2=4倍,
所以题干的说法是错误的.
故答案为:×.
12.解:“转化”是小学阶段研究平面图形面积的计算方法常用的思想方法,如:探索平行四边形面积的计算方法、圆面积的计算方法等都是通过转化得来的;另外,在学习了倒数之后,探索分数除法的计算方法,也是通过转化,除以一个不为0的数,转化为乘这个数的倒数.
因此,通过转化的方法,探索出了分数除法和圆面积的计算方法.此说法是正确的.
故答案为:√.
13.解:根据分析可得,
当一个圆的周长扩大到原来的3倍,圆的半径扩大3倍,面积扩大32=9倍;所以原题说法错误.
故答案为:×.
14.解:3.14×[(4÷2)2﹣(2÷2)2]
=3.14×[4﹣1]
=3.14×3
=9.42(平方米)
答:这个环形的面积是9.42平方米。
9.42≠37.68
故答案为:×。
四.计算题(共1小题)
15.解:8÷2=4(米)
3.14×(52﹣42)
=3.14×(25﹣16)
=3.14×9
=28.26(平方米)
答:圆环的面积是28.26平方米。
五.应用题(共6小题)
16.解:3.14×(6÷2+1)2﹣3.14×(6÷2)2
=3.14×42﹣3.14×32
=3.14×(16﹣9)
=3.14×7
=21.98(平方厘米)
21.98÷2=10.99(平方厘米)
答:把它平放在桌子上,所占面积是10.99平方厘米.
17.解:314÷3.14=100(平方米)
因为10×10=100
所以圆的半径是10米,
3.14×10×2
=31.4×2
=62.8(米)
答:绕这个花坛走一圈,有62.8米.
18.解:25.12÷3.14÷2
=8÷2
=4(米);
3.14×42
=3.14×16
=50.24(平方米)
答:它的面积是50.24平方米.
19.解:18.84÷3.14=6(分米)
6×6=36(平方分米)
答:这块铁板的面积是36平方分米.
20.解:3.14×(10÷2+3)2﹣3.14×(10÷2)2
=3.14×64﹣3.14×25
=3.14×(64﹣25)
=122.46(平方米).
答:这条小路的面积是122.46平方米.
21.解:10÷2=5(厘米)
3.14×5×2=31.4(厘米)
3.14×52
=3.14×25
=78.5(平方厘米)
答:这个圆的周长是31.4厘米,面积是78.5平方厘米.
