2021-2022学年人教版八年级数学上册11.1..2 三角形的高、中线与角平分线同步练习题(word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学上册11.1..2 三角形的高、中线与角平分线同步练习题(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 203.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-24 08:18:02 | ||
图片预览

文档简介
11.1.2 三角形的高、中线与角平分线同步练习题
2021-2022学年人教版八年级数学上册
基础题
知识点1 三角形的高
1.如图,AD是△ABC的边BC上的高,则AD与BC的位置关系是_____,∠ADB=_____=_____.
2.如图,用三角板作△ABC的边AB上的高线,下列三角板的摆放位置正确的是(
)
3.锐角三角形的三条高都在三角形内部,钝角三角形有2条高在三角形外,直角三角形有两条高恰是它的_____.
4.如图,在△ABC中,∠C=90°.
(1)指出图中BC,AC边上的高;
(2)画出AB边上的高CD;
(3)在(2)的条件下,图中有几个直角三角形?分别表示出来;
(4)若BC=3,AC=4,AB=5,求AB边上的高CD的长.
知识点2 三角形的中线
5.如图,AD是△ABC的中线,则点D是线段_____的中点,BD=CD=_____,S△ABD=_____=_____.
6.三角形的三条中线相交于一点,这个点一定在三角形的内部,这个点叫做三角形的_____.
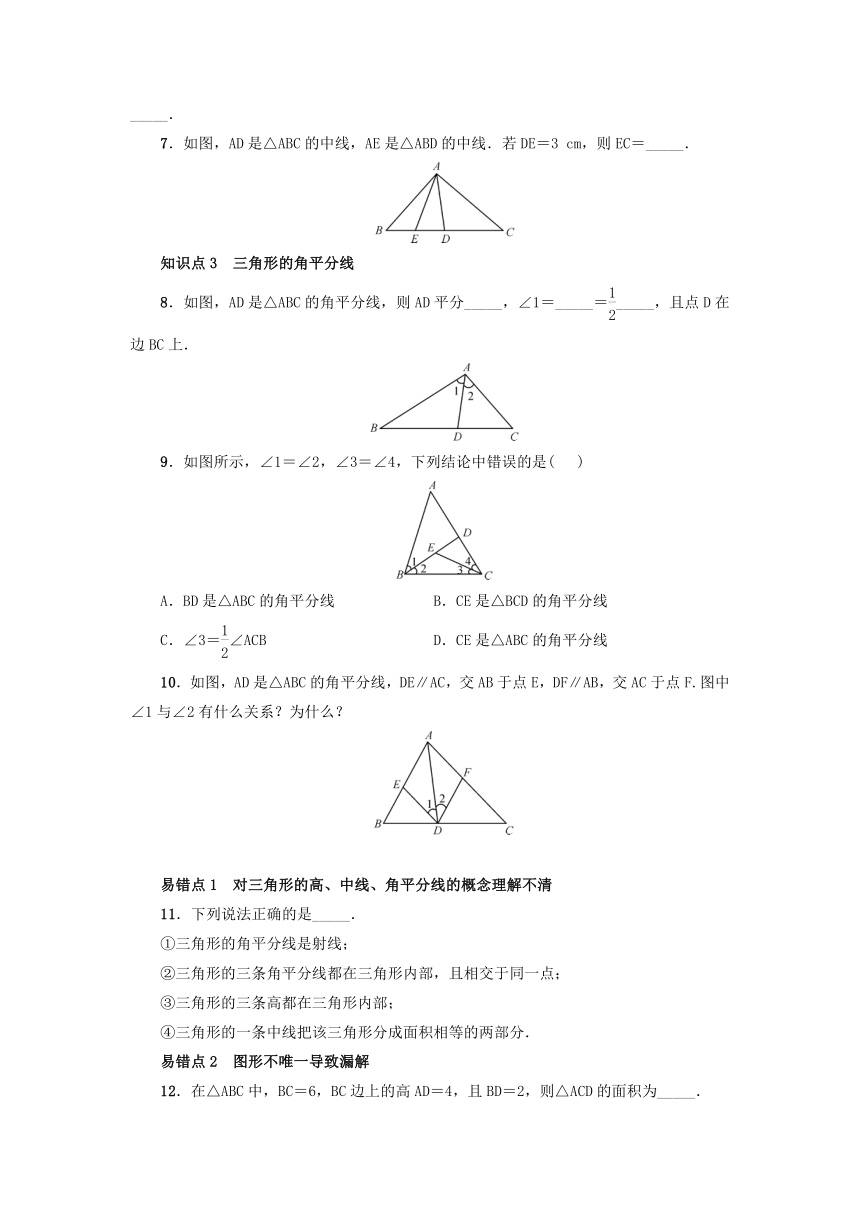
7.如图,AD是△ABC的中线,AE是△ABD的中线.若DE=3
cm,则EC=_____.
知识点3 三角形的角平分线
8.如图,AD是△ABC的角平分线,则AD平分_____,∠1=_____=_____,且点D在边BC上.
9.如图所示,∠1=∠2,∠3=∠4,下列结论中错误的是(
)
A.BD是△ABC的角平分线
B.CE是△BCD的角平分线
C.∠3=∠ACB
D.CE是△ABC的角平分线
10.如图,AD是△ABC的角平分线,DE∥AC,交AB于点E,DF∥AB,交AC于点F.图中∠1与∠2有什么关系?为什么?
易错点1 对三角形的高、中线、角平分线的概念理解不清
11.下列说法正确的是_____.
①三角形的角平分线是射线;
②三角形的三条角平分线都在三角形内部,且相交于同一点;
③三角形的三条高都在三角形内部;
④三角形的一条中线把该三角形分成面积相等的两部分.
易错点2 图形不唯一导致漏解
12.在△ABC中,BC=6,BC边上的高AD=4,且BD=2,则△ACD的面积为_____.
中档题
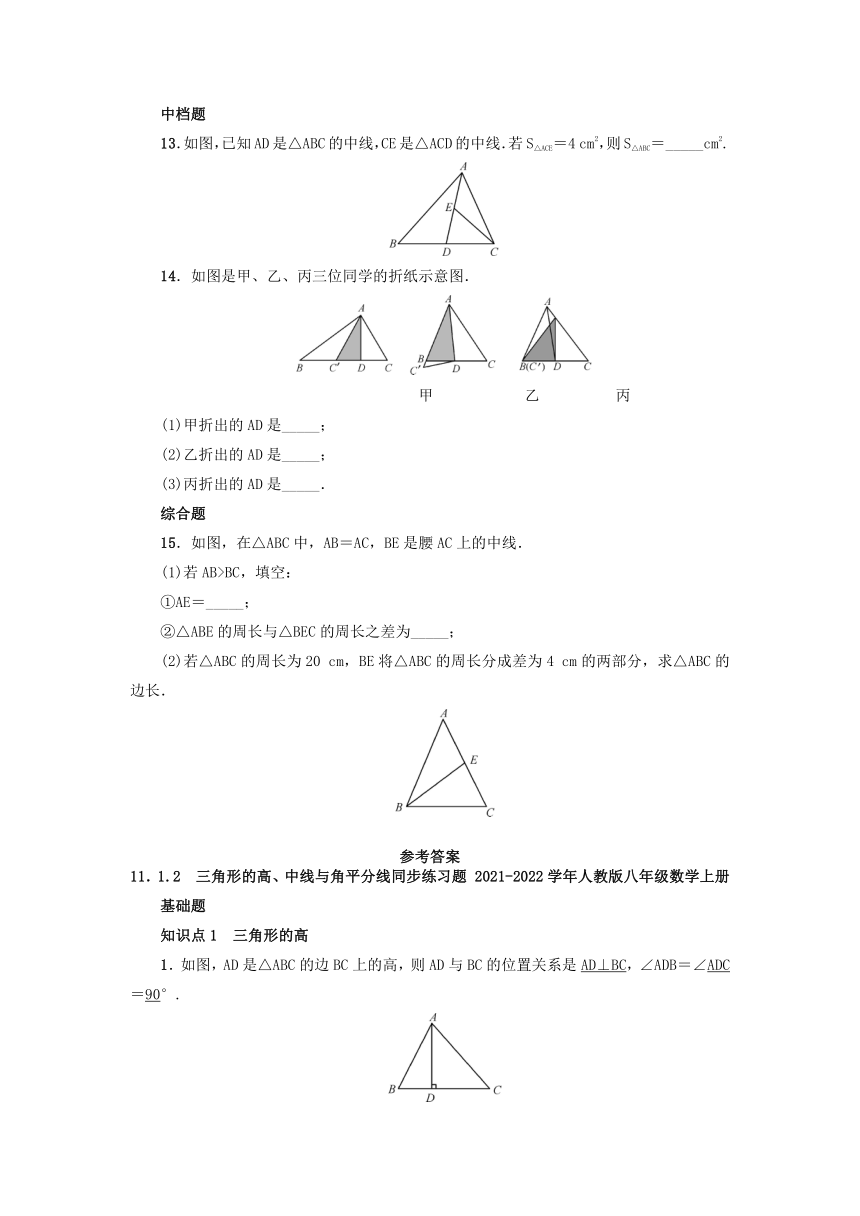
13.如图,已知AD是△ABC的中线,CE是△ACD的中线.若S△ACE=4
cm2,则S△ABC=_____cm2.
14.如图是甲、乙、丙三位同学的折纸示意图.
甲 乙 丙
(1)甲折出的AD是_____;
(2)乙折出的AD是_____;
(3)丙折出的AD是_____.
综合题
15.如图,在△ABC中,AB=AC,BE是腰AC上的中线.
(1)若AB>BC,填空:
①AE=_____;
②△ABE的周长与△BEC的周长之差为_____;
(2)若△ABC的周长为20
cm,BE将△ABC的周长分成差为4
cm的两部分,求△ABC的边长.
参考答案
11.1.2 三角形的高、中线与角平分线同步练习题
2021-2022学年人教版八年级数学上册
基础题
知识点1 三角形的高
1.如图,AD是△ABC的边BC上的高,则AD与BC的位置关系是AD⊥BC,∠ADB=∠ADC=90°.
2.如图,用三角板作△ABC的边AB上的高线,下列三角板的摆放位置正确的是(B)
3.锐角三角形的三条高都在三角形内部,钝角三角形有2条高在三角形外,直角三角形有两条高恰是它的直角边.
4.如图,在△ABC中,∠C=90°.
(1)指出图中BC,AC边上的高;
(2)画出AB边上的高CD;
(3)在(2)的条件下,图中有几个直角三角形?分别表示出来;
(4)若BC=3,AC=4,AB=5,求AB边上的高CD的长.
解:(1)BC边上的高是AC,AC边上的高是BC.
(2)如图所示.
(3)图中有3个直角三角形,分别是直角三角形ABC,直角三角形ACD,直角三角形BCD.
(4)∵S△ABC=AC·BC=AB·CD,
∴CD===2.4.
知识点2 三角形的中线
5.如图,AD是△ABC的中线,则点D是线段BC的中点,BD=CD=BC,S△ABD=S△ACD=S△ABC.
6.三角形的三条中线相交于一点,这个点一定在三角形的内部,这个点叫做三角形的重心.
7.如图,AD是△ABC的中线,AE是△ABD的中线.若DE=3
cm,则EC=9_cm.
知识点3 三角形的角平分线
8.如图,AD是△ABC的角平分线,则AD平分∠BAC,∠1=∠2=∠BAC,且点D在边BC上.
9.如图所示,∠1=∠2,∠3=∠4,下列结论中错误的是(D)
A.BD是△ABC的角平分线
B.CE是△BCD的角平分线
C.∠3=∠ACB
D.CE是△ABC的角平分线
10.如图,AD是△ABC的角平分线,DE∥AC,交AB于点E,DF∥AB,交AC于点F.图中∠1与∠2有什么关系?为什么?
解:∠1=∠2.理由:
∵DE∥AC,
∴∠1=∠DAC.
∵DF∥AB,
∴∠2=∠BAD.
∵AD是△ABC的角平分线,
∴∠BAD=∠DAC.
∴∠1=∠2.
易错点1 对三角形的高、中线、角平分线的概念理解不清
11.下列说法正确的是②④.
①三角形的角平分线是射线;
②三角形的三条角平分线都在三角形内部,且相交于同一点;
③三角形的三条高都在三角形内部;
④三角形的一条中线把该三角形分成面积相等的两部分.
易错点2 图形不唯一导致漏解
12.在△ABC中,BC=6,BC边上的高AD=4,且BD=2,则△ACD的面积为8或16.
中档题
13.如图,已知AD是△ABC的中线,CE是△ACD的中线.若S△ACE=4
cm2,则S△ABC=16cm2.
14.如图是甲、乙、丙三位同学的折纸示意图.
甲 乙 丙
(1)甲折出的AD是BC边上的高;
(2)乙折出的AD是∠BAC的平分线;
(3)丙折出的AD是BC边上的中线.
综合题
15.如图,在△ABC中,AB=AC,BE是腰AC上的中线.
(1)若AB>BC,填空:
①AE=EC;
②△ABE的周长与△BEC的周长之差为AB-BC;
(2)若△ABC的周长为20
cm,BE将△ABC的周长分成差为4
cm的两部分,求△ABC的边长.
解:设AB=x
cm,BC=y
cm,
当x>y时,
解得
即三边长分别为8
cm,8
cm,4
cm;
当x即三边长分别为
cm,
cm,
cm.
2021-2022学年人教版八年级数学上册
基础题
知识点1 三角形的高
1.如图,AD是△ABC的边BC上的高,则AD与BC的位置关系是_____,∠ADB=_____=_____.
2.如图,用三角板作△ABC的边AB上的高线,下列三角板的摆放位置正确的是(
)
3.锐角三角形的三条高都在三角形内部,钝角三角形有2条高在三角形外,直角三角形有两条高恰是它的_____.
4.如图,在△ABC中,∠C=90°.
(1)指出图中BC,AC边上的高;
(2)画出AB边上的高CD;
(3)在(2)的条件下,图中有几个直角三角形?分别表示出来;
(4)若BC=3,AC=4,AB=5,求AB边上的高CD的长.
知识点2 三角形的中线
5.如图,AD是△ABC的中线,则点D是线段_____的中点,BD=CD=_____,S△ABD=_____=_____.
6.三角形的三条中线相交于一点,这个点一定在三角形的内部,这个点叫做三角形的_____.
7.如图,AD是△ABC的中线,AE是△ABD的中线.若DE=3
cm,则EC=_____.
知识点3 三角形的角平分线
8.如图,AD是△ABC的角平分线,则AD平分_____,∠1=_____=_____,且点D在边BC上.
9.如图所示,∠1=∠2,∠3=∠4,下列结论中错误的是(
)
A.BD是△ABC的角平分线
B.CE是△BCD的角平分线
C.∠3=∠ACB
D.CE是△ABC的角平分线
10.如图,AD是△ABC的角平分线,DE∥AC,交AB于点E,DF∥AB,交AC于点F.图中∠1与∠2有什么关系?为什么?
易错点1 对三角形的高、中线、角平分线的概念理解不清
11.下列说法正确的是_____.
①三角形的角平分线是射线;
②三角形的三条角平分线都在三角形内部,且相交于同一点;
③三角形的三条高都在三角形内部;
④三角形的一条中线把该三角形分成面积相等的两部分.
易错点2 图形不唯一导致漏解
12.在△ABC中,BC=6,BC边上的高AD=4,且BD=2,则△ACD的面积为_____.
中档题
13.如图,已知AD是△ABC的中线,CE是△ACD的中线.若S△ACE=4
cm2,则S△ABC=_____cm2.
14.如图是甲、乙、丙三位同学的折纸示意图.
甲 乙 丙
(1)甲折出的AD是_____;
(2)乙折出的AD是_____;
(3)丙折出的AD是_____.
综合题
15.如图,在△ABC中,AB=AC,BE是腰AC上的中线.
(1)若AB>BC,填空:
①AE=_____;
②△ABE的周长与△BEC的周长之差为_____;
(2)若△ABC的周长为20
cm,BE将△ABC的周长分成差为4
cm的两部分,求△ABC的边长.
参考答案
11.1.2 三角形的高、中线与角平分线同步练习题
2021-2022学年人教版八年级数学上册
基础题
知识点1 三角形的高
1.如图,AD是△ABC的边BC上的高,则AD与BC的位置关系是AD⊥BC,∠ADB=∠ADC=90°.
2.如图,用三角板作△ABC的边AB上的高线,下列三角板的摆放位置正确的是(B)
3.锐角三角形的三条高都在三角形内部,钝角三角形有2条高在三角形外,直角三角形有两条高恰是它的直角边.
4.如图,在△ABC中,∠C=90°.
(1)指出图中BC,AC边上的高;
(2)画出AB边上的高CD;
(3)在(2)的条件下,图中有几个直角三角形?分别表示出来;
(4)若BC=3,AC=4,AB=5,求AB边上的高CD的长.
解:(1)BC边上的高是AC,AC边上的高是BC.
(2)如图所示.
(3)图中有3个直角三角形,分别是直角三角形ABC,直角三角形ACD,直角三角形BCD.
(4)∵S△ABC=AC·BC=AB·CD,
∴CD===2.4.
知识点2 三角形的中线
5.如图,AD是△ABC的中线,则点D是线段BC的中点,BD=CD=BC,S△ABD=S△ACD=S△ABC.
6.三角形的三条中线相交于一点,这个点一定在三角形的内部,这个点叫做三角形的重心.
7.如图,AD是△ABC的中线,AE是△ABD的中线.若DE=3
cm,则EC=9_cm.
知识点3 三角形的角平分线
8.如图,AD是△ABC的角平分线,则AD平分∠BAC,∠1=∠2=∠BAC,且点D在边BC上.
9.如图所示,∠1=∠2,∠3=∠4,下列结论中错误的是(D)
A.BD是△ABC的角平分线
B.CE是△BCD的角平分线
C.∠3=∠ACB
D.CE是△ABC的角平分线
10.如图,AD是△ABC的角平分线,DE∥AC,交AB于点E,DF∥AB,交AC于点F.图中∠1与∠2有什么关系?为什么?
解:∠1=∠2.理由:
∵DE∥AC,
∴∠1=∠DAC.
∵DF∥AB,
∴∠2=∠BAD.
∵AD是△ABC的角平分线,
∴∠BAD=∠DAC.
∴∠1=∠2.
易错点1 对三角形的高、中线、角平分线的概念理解不清
11.下列说法正确的是②④.
①三角形的角平分线是射线;
②三角形的三条角平分线都在三角形内部,且相交于同一点;
③三角形的三条高都在三角形内部;
④三角形的一条中线把该三角形分成面积相等的两部分.
易错点2 图形不唯一导致漏解
12.在△ABC中,BC=6,BC边上的高AD=4,且BD=2,则△ACD的面积为8或16.
中档题
13.如图,已知AD是△ABC的中线,CE是△ACD的中线.若S△ACE=4
cm2,则S△ABC=16cm2.
14.如图是甲、乙、丙三位同学的折纸示意图.
甲 乙 丙
(1)甲折出的AD是BC边上的高;
(2)乙折出的AD是∠BAC的平分线;
(3)丙折出的AD是BC边上的中线.
综合题
15.如图,在△ABC中,AB=AC,BE是腰AC上的中线.
(1)若AB>BC,填空:
①AE=EC;
②△ABE的周长与△BEC的周长之差为AB-BC;
(2)若△ABC的周长为20
cm,BE将△ABC的周长分成差为4
cm的两部分,求△ABC的边长.
解:设AB=x
cm,BC=y
cm,
当x>y时,
解得
即三边长分别为8
cm,8
cm,4
cm;
当x
cm,
cm,
cm.
