2021-2022学年人教版数学八年级上册11.2.1.1三角形的内角和 同步练习题(word版含答案)
文档属性
| 名称 | 2021-2022学年人教版数学八年级上册11.2.1.1三角形的内角和 同步练习题(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 106.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-24 08:31:53 | ||
图片预览


文档简介
11.2.1.1三角形的内角和
同步练习题
2021-2022学年人教版八年级数学上册
A组
(基础题)
1.如图,在△ABC中,∠A=60°,∠B=40°,则∠C等于(
)
A.100°
B.80°
C.60°
D.40°
2.在△ABC中,∠A,∠B,∠C的度数之比为2∶3∶4,则∠B的度数为(
)
A.120°
B.80°
C.60°
D.40°
3.在△ABC中,∠A=55°,∠B比∠C大25°,则∠B等于(
)
A.50°
B.75°
C.100°
D.125°
4.写出下列图中x的值:
(1)x=________;
(2)x=_______.
5.如图,在△ABC中,AD平分∠BAC,∠B=70°,∠BAD=30°,则∠C的度数为(
)
A.35°
B.40°
C.45°
D.50°
6.如图,在△ABC中,∠C=90°,AD平分∠BAC,且∠B=3∠BAD,求∠B的度数.
7.如图,在△ABC中,∠A=60°,∠B=40°,DE∥BC,则∠AED的度数是(
)
A.50°
B.60°
C.70°
D.80°
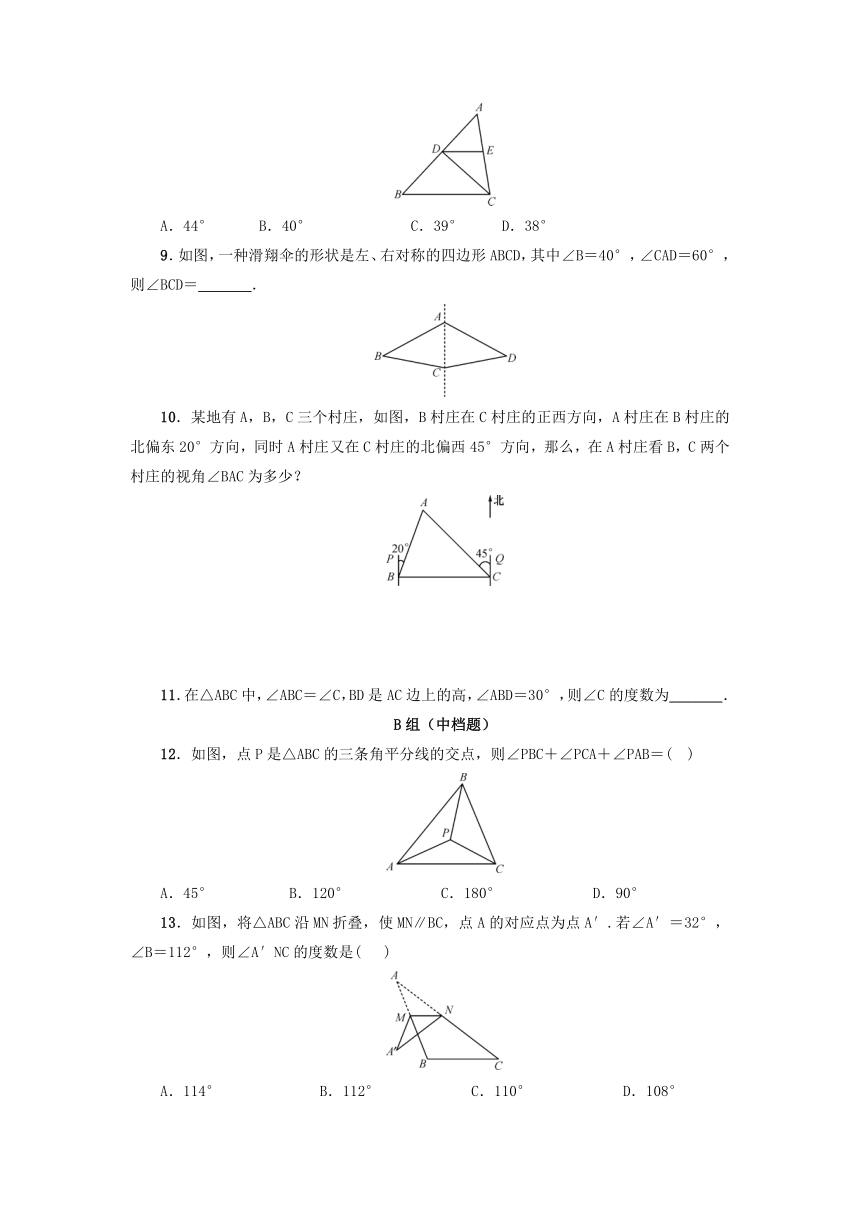
8.如图,在△ABC中,CD平分∠ACB交AB于点D,过点D作DE∥BC交AC于点E.若∠A=54°,∠B=48°,则∠CDE的大小为(
)
A.44°
B.40°
C.39°
D.38°
9.如图,一种滑翔伞的形状是左、右对称的四边形ABCD,其中∠B=40°,∠CAD=60°,则∠BCD=_______.
10.某地有A,B,C三个村庄,如图,B村庄在C村庄的正西方向,A村庄在B村庄的北偏东20°方向,同时A村庄又在C村庄的北偏西45°方向,那么,在A村庄看B,C两个村庄的视角∠BAC为多少?
11.在△ABC中,∠ABC=∠C,BD是AC边上的高,∠ABD=30°,则∠C的度数为_______.
B组(中档题)
12.如图,点P是△ABC的三条角平分线的交点,则∠PBC+∠PCA+∠PAB=(
)
A.45°
B.120°
C.180°
D.90°
13.如图,将△ABC沿MN折叠,使MN∥BC,点A的对应点为点A′.若∠A′=32°,∠B=112°,则∠A′NC的度数是(
)
A.114°
B.112°
C.110°
D.108°
14.(1)如图,在△ABC中,∠ABC,∠ACB的平分线BE,CD相交于点F,∠A=58°,则∠BFC=_______.
(2)如图是A,B,C三岛的平面图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏东30°方向,则从C岛看A,B两岛的视角∠ACB=_______.
15.如图,已知在△ABC中,∠B=∠C,D为边BC上一点(不与B,C重合),点E为边AC上一点,∠ADE=∠AED,∠BAC=44°.
(1)求∠C的度数;
(2)若∠ADE=75°,求∠CDE的度数.
C组(综合题)
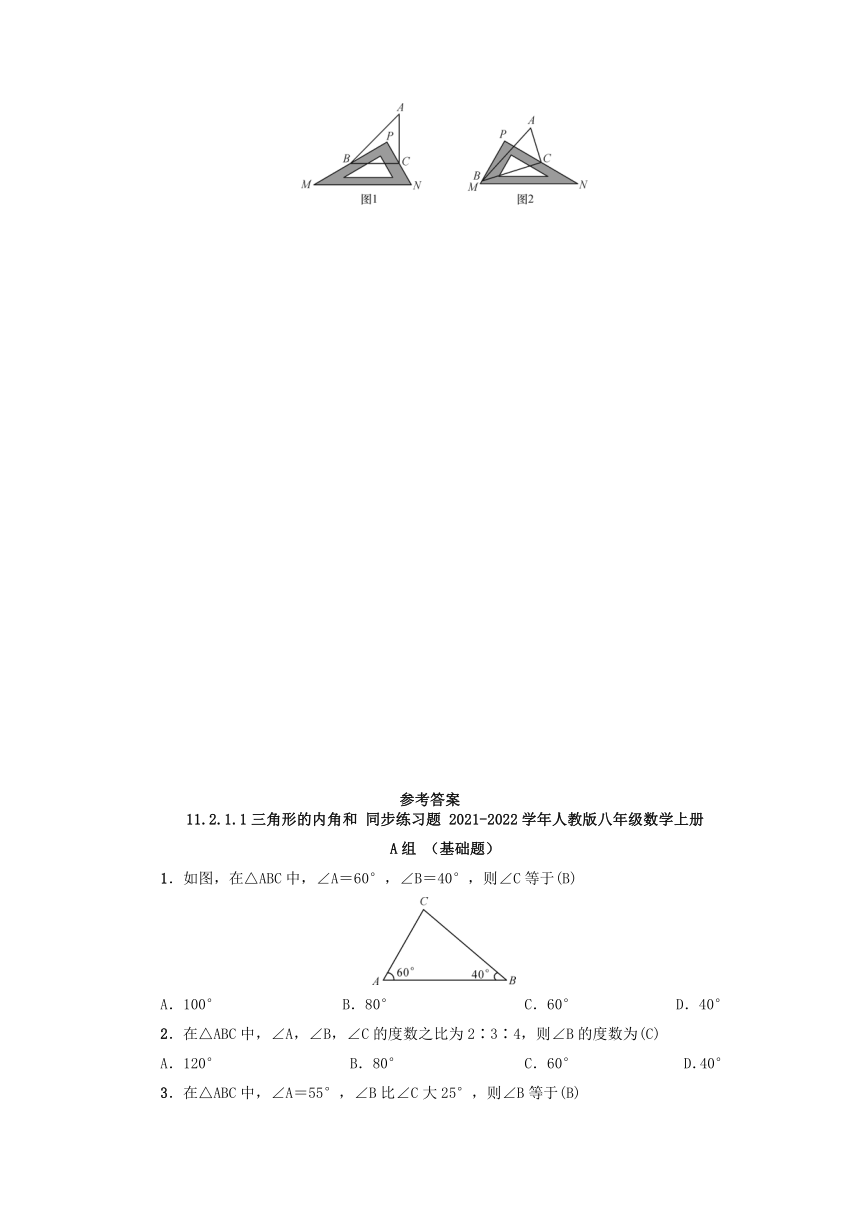
16.问题情景:如图1,将一块直角三角板PMN放置在△ABC上(P点在△ABC内),使三角板PMN的两条直角边PM,PN恰好分别经过点B和点C.试问∠ABP与∠ACP是否存在某种确定的数量关系?
(1)特殊探究:若∠A=50°,则∠ABC+∠ACB=_______,∠PBC+∠PCB=_______,∠ABP+∠ACP=_______;
(2)类比探究:请探究∠ABP+∠ACP与∠A的数量关系;
(3)类比延伸:如图2,改变直角三角板PMN的位置,使P点在△ABC外,直角三角板PMN的两条直角边PM,PN仍然分别经过点B和点C,(2)中的结论是否仍然成立?若不成立,请直接写出你的结论.
参考答案
11.2.1.1三角形的内角和
同步练习题
2021-2022学年人教版八年级数学上册
A组
(基础题)
1.如图,在△ABC中,∠A=60°,∠B=40°,则∠C等于(B)
A.100°
B.80°
C.60°
D.40°
2.在△ABC中,∠A,∠B,∠C的度数之比为2∶3∶4,则∠B的度数为(C)
A.120°
B.80°
C.60°
D.40°
3.在△ABC中,∠A=55°,∠B比∠C大25°,则∠B等于(B)
A.50°
B.75°
C.100°
D.125°
4.写出下列图中x的值:
(1)x=45;
(2)x=75.
5.如图,在△ABC中,AD平分∠BAC,∠B=70°,∠BAD=30°,则∠C的度数为(D)
A.35°
B.40°
C.45°
D.50°
6.如图,在△ABC中,∠C=90°,AD平分∠BAC,且∠B=3∠BAD,求∠B的度数.
解:∵AD平分∠BAC,
∴∠BAD=∠BAC.
∵∠BAC+∠B+∠C=180°,∠B=3∠BAD,
∴2∠BAD+3∠BAD+90°=180°.
∴∠BAD=18°.
∴∠B=3∠BAD=54°.
7.如图,在△ABC中,∠A=60°,∠B=40°,DE∥BC,则∠AED的度数是(D)
A.50°
B.60°
C.70°
D.80°
8.如图,在△ABC中,CD平分∠ACB交AB于点D,过点D作DE∥BC交AC于点E.若∠A=54°,∠B=48°,则∠CDE的大小为(C)
A.44°
B.40°
C.39°
D.38°
9.如图,一种滑翔伞的形状是左、右对称的四边形ABCD,其中∠B=40°,∠CAD=60°,则∠BCD=160°.
10.某地有A,B,C三个村庄,如图,B村庄在C村庄的正西方向,A村庄在B村庄的北偏东20°方向,同时A村庄又在C村庄的北偏西45°方向,那么,在A村庄看B,C两个村庄的视角∠BAC为多少?
解:由A村庄在B村庄的北偏东20°方向,得∠ABC=∠PBC-∠PBA=90°-20°=70°.
由A村庄在C村庄的北偏西45°方向,得∠ACB=∠QCB-∠ACQ=90°-45°=45°.
∴∠BAC=180°-∠ABC-∠ACB=180°-70°-45°=65°.
∴在A村庄看B,C两个村庄的视角∠BAC的大小是65°.
11.在△ABC中,∠ABC=∠C,BD是AC边上的高,∠ABD=30°,则∠C的度数为60°或30°.
B组(中档题)
12.如图,点P是△ABC的三条角平分线的交点,则∠PBC+∠PCA+∠PAB=(D)
A.45°
B.120°
C.180°
D.90°
13.如图,将△ABC沿MN折叠,使MN∥BC,点A的对应点为点A′.若∠A′=32°,∠B=112°,则∠A′NC的度数是(D)
A.114°
B.112°
C.110°
D.108°
14.(1)如图,在△ABC中,∠ABC,∠ACB的平分线BE,CD相交于点F,∠A=58°,则∠BFC=119°.
(2)如图是A,B,C三岛的平面图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏东30°方向,则从C岛看A,B两岛的视角∠ACB=20°.
15.如图,已知在△ABC中,∠B=∠C,D为边BC上一点(不与B,C重合),点E为边AC上一点,∠ADE=∠AED,∠BAC=44°.
(1)求∠C的度数;
(2)若∠ADE=75°,求∠CDE的度数.
解:(1)∵∠BAC=44°,
∴∠B+∠C=180°-∠BAC=180°-44°=136°.
∵∠B=∠C,∴2∠C=136°.
∴∠C=68°.
(2)∵∠ADE=∠AED,∠ADE=75°,
∴∠AED=75°.
∵∠AED+∠CED=180°,
∴∠CED=180°-75°=105°.
∵∠CDE+∠CED+∠C=180°,
∴∠CDE=180°-105°-68°=7°.
C组(综合题)
16.问题情景:如图1,将一块直角三角板PMN放置在△ABC上(P点在△ABC内),使三角板PMN的两条直角边PM,PN恰好分别经过点B和点C.试问∠ABP与∠ACP是否存在某种确定的数量关系?
(1)特殊探究:若∠A=50°,则∠ABC+∠ACB=130°,∠PBC+∠PCB=90°,∠ABP+∠ACP=40°;
(2)类比探究:请探究∠ABP+∠ACP与∠A的数量关系;
(3)类比延伸:如图2,改变直角三角板PMN的位置,使P点在△ABC外,直角三角板PMN的两条直角边PM,PN仍然分别经过点B和点C,(2)中的结论是否仍然成立?若不成立,请直接写出你的结论.
解:(2)∠ABP+∠ACP=90°-∠A.
∵在△ABC中,∠A+∠ABC+∠ACB=180°,即∠A+(∠ABP+∠PBC)+(∠ACP+∠PCB)=180°,
在△PBC中,∠P+∠PBC+∠PCB=180°,即∠PBC+∠PCB=90°,
∴∠A+(∠ABP+∠ACP)+90°=180°.
∴∠ABP+∠ACP+∠A=90°.
∴∠ABP+∠ACP=90°-∠A.
(3)不成立,∠ACP-∠ABP=90°-∠A.
同步练习题
2021-2022学年人教版八年级数学上册
A组
(基础题)
1.如图,在△ABC中,∠A=60°,∠B=40°,则∠C等于(
)
A.100°
B.80°
C.60°
D.40°
2.在△ABC中,∠A,∠B,∠C的度数之比为2∶3∶4,则∠B的度数为(
)
A.120°
B.80°
C.60°
D.40°
3.在△ABC中,∠A=55°,∠B比∠C大25°,则∠B等于(
)
A.50°
B.75°
C.100°
D.125°
4.写出下列图中x的值:
(1)x=________;
(2)x=_______.
5.如图,在△ABC中,AD平分∠BAC,∠B=70°,∠BAD=30°,则∠C的度数为(
)
A.35°
B.40°
C.45°
D.50°
6.如图,在△ABC中,∠C=90°,AD平分∠BAC,且∠B=3∠BAD,求∠B的度数.
7.如图,在△ABC中,∠A=60°,∠B=40°,DE∥BC,则∠AED的度数是(
)
A.50°
B.60°
C.70°
D.80°
8.如图,在△ABC中,CD平分∠ACB交AB于点D,过点D作DE∥BC交AC于点E.若∠A=54°,∠B=48°,则∠CDE的大小为(
)
A.44°
B.40°
C.39°
D.38°
9.如图,一种滑翔伞的形状是左、右对称的四边形ABCD,其中∠B=40°,∠CAD=60°,则∠BCD=_______.
10.某地有A,B,C三个村庄,如图,B村庄在C村庄的正西方向,A村庄在B村庄的北偏东20°方向,同时A村庄又在C村庄的北偏西45°方向,那么,在A村庄看B,C两个村庄的视角∠BAC为多少?
11.在△ABC中,∠ABC=∠C,BD是AC边上的高,∠ABD=30°,则∠C的度数为_______.
B组(中档题)
12.如图,点P是△ABC的三条角平分线的交点,则∠PBC+∠PCA+∠PAB=(
)
A.45°
B.120°
C.180°
D.90°
13.如图,将△ABC沿MN折叠,使MN∥BC,点A的对应点为点A′.若∠A′=32°,∠B=112°,则∠A′NC的度数是(
)
A.114°
B.112°
C.110°
D.108°
14.(1)如图,在△ABC中,∠ABC,∠ACB的平分线BE,CD相交于点F,∠A=58°,则∠BFC=_______.
(2)如图是A,B,C三岛的平面图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏东30°方向,则从C岛看A,B两岛的视角∠ACB=_______.
15.如图,已知在△ABC中,∠B=∠C,D为边BC上一点(不与B,C重合),点E为边AC上一点,∠ADE=∠AED,∠BAC=44°.
(1)求∠C的度数;
(2)若∠ADE=75°,求∠CDE的度数.
C组(综合题)
16.问题情景:如图1,将一块直角三角板PMN放置在△ABC上(P点在△ABC内),使三角板PMN的两条直角边PM,PN恰好分别经过点B和点C.试问∠ABP与∠ACP是否存在某种确定的数量关系?
(1)特殊探究:若∠A=50°,则∠ABC+∠ACB=_______,∠PBC+∠PCB=_______,∠ABP+∠ACP=_______;
(2)类比探究:请探究∠ABP+∠ACP与∠A的数量关系;
(3)类比延伸:如图2,改变直角三角板PMN的位置,使P点在△ABC外,直角三角板PMN的两条直角边PM,PN仍然分别经过点B和点C,(2)中的结论是否仍然成立?若不成立,请直接写出你的结论.
参考答案
11.2.1.1三角形的内角和
同步练习题
2021-2022学年人教版八年级数学上册
A组
(基础题)
1.如图,在△ABC中,∠A=60°,∠B=40°,则∠C等于(B)
A.100°
B.80°
C.60°
D.40°
2.在△ABC中,∠A,∠B,∠C的度数之比为2∶3∶4,则∠B的度数为(C)
A.120°
B.80°
C.60°
D.40°
3.在△ABC中,∠A=55°,∠B比∠C大25°,则∠B等于(B)
A.50°
B.75°
C.100°
D.125°
4.写出下列图中x的值:
(1)x=45;
(2)x=75.
5.如图,在△ABC中,AD平分∠BAC,∠B=70°,∠BAD=30°,则∠C的度数为(D)
A.35°
B.40°
C.45°
D.50°
6.如图,在△ABC中,∠C=90°,AD平分∠BAC,且∠B=3∠BAD,求∠B的度数.
解:∵AD平分∠BAC,
∴∠BAD=∠BAC.
∵∠BAC+∠B+∠C=180°,∠B=3∠BAD,
∴2∠BAD+3∠BAD+90°=180°.
∴∠BAD=18°.
∴∠B=3∠BAD=54°.
7.如图,在△ABC中,∠A=60°,∠B=40°,DE∥BC,则∠AED的度数是(D)
A.50°
B.60°
C.70°
D.80°
8.如图,在△ABC中,CD平分∠ACB交AB于点D,过点D作DE∥BC交AC于点E.若∠A=54°,∠B=48°,则∠CDE的大小为(C)
A.44°
B.40°
C.39°
D.38°
9.如图,一种滑翔伞的形状是左、右对称的四边形ABCD,其中∠B=40°,∠CAD=60°,则∠BCD=160°.
10.某地有A,B,C三个村庄,如图,B村庄在C村庄的正西方向,A村庄在B村庄的北偏东20°方向,同时A村庄又在C村庄的北偏西45°方向,那么,在A村庄看B,C两个村庄的视角∠BAC为多少?
解:由A村庄在B村庄的北偏东20°方向,得∠ABC=∠PBC-∠PBA=90°-20°=70°.
由A村庄在C村庄的北偏西45°方向,得∠ACB=∠QCB-∠ACQ=90°-45°=45°.
∴∠BAC=180°-∠ABC-∠ACB=180°-70°-45°=65°.
∴在A村庄看B,C两个村庄的视角∠BAC的大小是65°.
11.在△ABC中,∠ABC=∠C,BD是AC边上的高,∠ABD=30°,则∠C的度数为60°或30°.
B组(中档题)
12.如图,点P是△ABC的三条角平分线的交点,则∠PBC+∠PCA+∠PAB=(D)
A.45°
B.120°
C.180°
D.90°
13.如图,将△ABC沿MN折叠,使MN∥BC,点A的对应点为点A′.若∠A′=32°,∠B=112°,则∠A′NC的度数是(D)
A.114°
B.112°
C.110°
D.108°
14.(1)如图,在△ABC中,∠ABC,∠ACB的平分线BE,CD相交于点F,∠A=58°,则∠BFC=119°.
(2)如图是A,B,C三岛的平面图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏东30°方向,则从C岛看A,B两岛的视角∠ACB=20°.
15.如图,已知在△ABC中,∠B=∠C,D为边BC上一点(不与B,C重合),点E为边AC上一点,∠ADE=∠AED,∠BAC=44°.
(1)求∠C的度数;
(2)若∠ADE=75°,求∠CDE的度数.
解:(1)∵∠BAC=44°,
∴∠B+∠C=180°-∠BAC=180°-44°=136°.
∵∠B=∠C,∴2∠C=136°.
∴∠C=68°.
(2)∵∠ADE=∠AED,∠ADE=75°,
∴∠AED=75°.
∵∠AED+∠CED=180°,
∴∠CED=180°-75°=105°.
∵∠CDE+∠CED+∠C=180°,
∴∠CDE=180°-105°-68°=7°.
C组(综合题)
16.问题情景:如图1,将一块直角三角板PMN放置在△ABC上(P点在△ABC内),使三角板PMN的两条直角边PM,PN恰好分别经过点B和点C.试问∠ABP与∠ACP是否存在某种确定的数量关系?
(1)特殊探究:若∠A=50°,则∠ABC+∠ACB=130°,∠PBC+∠PCB=90°,∠ABP+∠ACP=40°;
(2)类比探究:请探究∠ABP+∠ACP与∠A的数量关系;
(3)类比延伸:如图2,改变直角三角板PMN的位置,使P点在△ABC外,直角三角板PMN的两条直角边PM,PN仍然分别经过点B和点C,(2)中的结论是否仍然成立?若不成立,请直接写出你的结论.
解:(2)∠ABP+∠ACP=90°-∠A.
∵在△ABC中,∠A+∠ABC+∠ACB=180°,即∠A+(∠ABP+∠PBC)+(∠ACP+∠PCB)=180°,
在△PBC中,∠P+∠PBC+∠PCB=180°,即∠PBC+∠PCB=90°,
∴∠A+(∠ABP+∠ACP)+90°=180°.
∴∠ABP+∠ACP+∠A=90°.
∴∠ABP+∠ACP=90°-∠A.
(3)不成立,∠ACP-∠ABP=90°-∠A.
