2021-2022学年人教版数学八年级上册11.3.2多边形的内角和 同步练习题 (word版含答案)
文档属性
| 名称 | 2021-2022学年人教版数学八年级上册11.3.2多边形的内角和 同步练习题 (word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 118.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-24 00:00:00 | ||
图片预览


文档简介
11.3.2多边形的内角和
同步练习题
2021-2022学年人教版八年级数学上册
A组(基础题)
1.如图,从多边形的一个顶点出发作它的对角线,结合图形完成下表:
多边形的边数
4
5
6
…
n
分成三角形的个数
…
多边形的内角和
…
2.已知一个多边形的内角和是1
080°,则这个多边形是(
)
A.五边形
B.六边形
C.七边形
D.八边形
3.如图,该硬币边缘镌刻的正九边形的每个内角的度数是_________.
4.求如图所示的图形中x的值:
5.(1)正十边形的外角和为______;
(2)已知正多边形的一个外角为36°,则该正多边形的边数为______.
6.如图,五边形ABCDE的外角中,∠1=∠2=∠3=∠4=75°,则∠A的度数是______.
7.一个多边形的内角和是外角和的2倍,这个多边形是几边形?
8.如果一个多边形的每个外角都相等,且比内角小36°,求这个多边形的边数和内角和.
9.把一个多边形割去一个角后,得到的多边形的内角和为1440°,则原多边形的边数为______.
B组(中档题)
10.如图,小明从点A出发沿直线前进10米到达点B,向左转45°后又沿直线前进10米到达点C,再向左转45°后沿直线前进10米到达点D,……,照这样走下去,小明第一次回到出发点A时所走的路程为(
)
A.100米
B.80米
C.60米
D.40米
11.将一个n边形变成(n+1)边形,内角和将(
)
A.减少180°
B.增加90°
C.增加180°
D.增加360°
12.如图,在五边形ABCDE中,若去掉一个30°的角后得到一个六边形BCDEMN,则∠1+∠2的度数为(
)
A.210°
B.110°
C.150°
D.100°
13.如图,∠A+∠B+∠C+∠D+∠E+∠F=______.
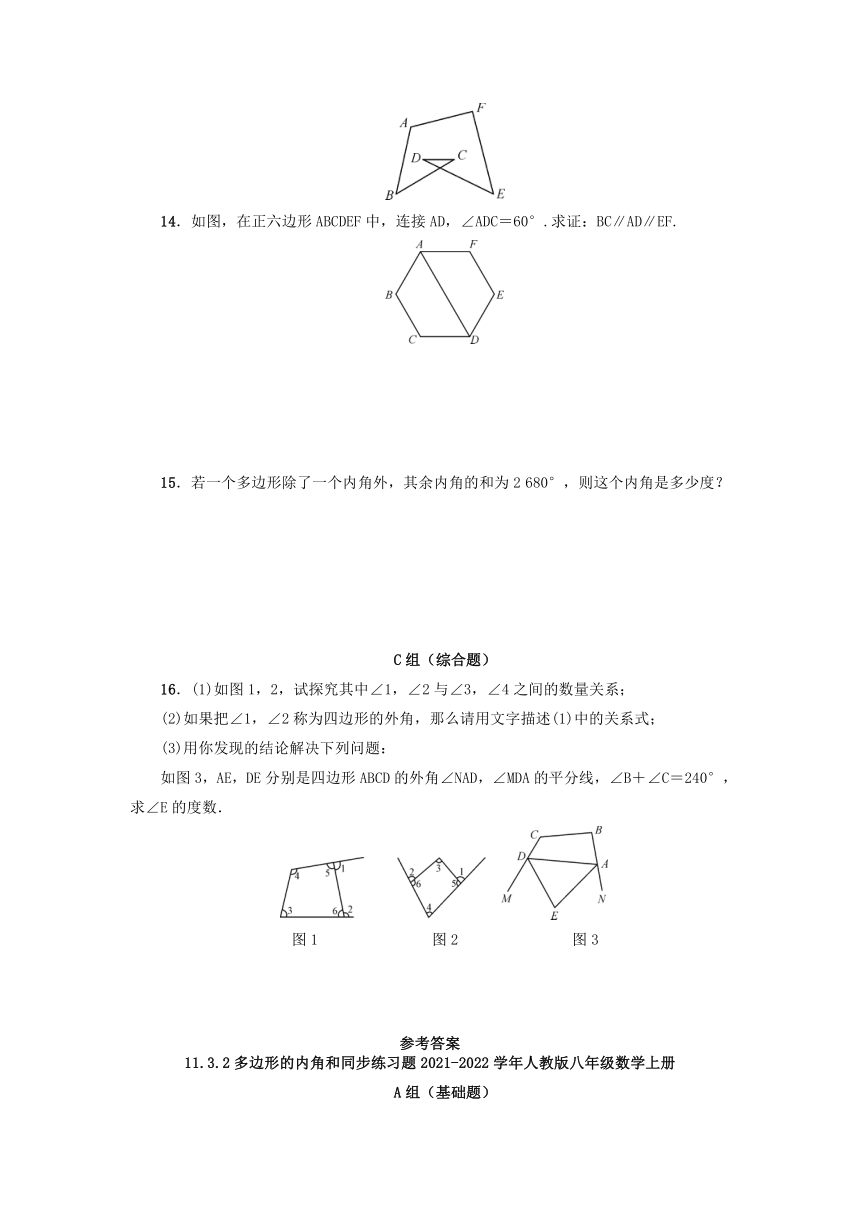
14.如图,在正六边形ABCDEF中,连接AD,∠ADC=60°.求证:BC∥AD∥EF.
15.若一个多边形除了一个内角外,其余内角的和为2
680°,则这个内角是多少度?
C组(综合题)
16.(1)如图1,2,试探究其中∠1,∠2与∠3,∠4之间的数量关系;
(2)如果把∠1,∠2称为四边形的外角,那么请用文字描述(1)中的关系式;
(3)用你发现的结论解决下列问题:
如图3,AE,DE分别是四边形ABCD的外角∠NAD,∠MDA的平分线,∠B+∠C=240°,求∠E的度数.
图1
图2
图3
参考答案
11.3.2多边形的内角和同步练习题2021-2022学年人教版八年级数学上册
A组(基础题)
1.如图,从多边形的一个顶点出发作它的对角线,结合图形完成下表:
多边形的边数
4
5
6
…
n
分成三角形的个数
2
3
4
…
n-2
多边形的内角和
360°
540°
720°
…
(n-2)×180°
2.已知一个多边形的内角和是1
080°,则这个多边形是(D)
A.五边形
B.六边形
C.七边形
D.八边形
3.如图,该硬币边缘镌刻的正九边形的每个内角的度数是140°.
4.求如图所示的图形中x的值:
解:(1)根据图形可知:x=360-150-90-70=50.
(2)根据图形可知:x=180-[360-(90+73+82)]=65.
(3)根据图形可知:x+x+30+60+x+x-10=(5-2)×180.解得x=115.
5.(1)正十边形的外角和为360°;
(2)已知正多边形的一个外角为36°,则该正多边形的边数为10.
6.如图,五边形ABCDE的外角中,∠1=∠2=∠3=∠4=75°,则∠A的度数是120°.
7.一个多边形的内角和是外角和的2倍,这个多边形是几边形?
解:设这个多边形的边数为n,由题意,得
(n-2)·180°=360°×2.
解得n=6.
答:这个多边形是六边形.
8.如果一个多边形的每个外角都相等,且比内角小36°,求这个多边形的边数和内角和.
解:设多边形的一个外角为x°,则一个内角为(x+36)°,依题意,得
x+x+36=180,
解得x=72.
360°÷72°=5,
(5-2)×180°=540°.
故这个多边形的边数为5,内角和是540°.
9.把一个多边形割去一个角后,得到的多边形的内角和为1
440°,则原多边形的边数为9或10或11.
B组(中档题)
10.如图,小明从点A出发沿直线前进10米到达点B,向左转45°后又沿直线前进10米到达点C,再向左转45°后沿直线前进10米到达点D,……,照这样走下去,小明第一次回到出发点A时所走的路程为(B)
A.100米
B.80米
C.60米
D.40米
11.将一个n边形变成(n+1)边形,内角和将(C)
A.减少180°
B.增加90°
C.增加180°
D.增加360°
12.如图,在五边形ABCDE中,若去掉一个30°的角后得到一个六边形BCDEMN,则∠1+∠2的度数为(A)
A.210°
B.110°
C.150°
D.100°
13.如图,∠A+∠B+∠C+∠D+∠E+∠F=360°.
14.如图,在正六边形ABCDEF中,连接AD,∠ADC=60°.求证:BC∥AD∥EF.
证明:正六边形的每个内角的度数为=120°,
∵∠ADC=60°,∠CDE=120°,
∴∠ADE=60°.
又∵∠C=∠E=120°,
∴∠C+∠ADC=180°,∠E+∠ADE=180°.
∴BC∥AD,AD∥EF.
∴BC∥AD∥EF.
15.若一个多边形除了一个内角外,其余内角的和为2
680°,则这个内角是多少度?
解:设这个内角度数为x°,边数为n,
则(n-2)×180-x=2
680,
∴n=.
∵n为正整数,0<x<180,
∴n=17.
∴这个内角度数为180°×(17-2)-2
680°=20°.
故这个内角的度数是20°.
C组(综合题)
16.(1)如图1,2,试探究其中∠1,∠2与∠3,∠4之间的数量关系;
(2)如果把∠1,∠2称为四边形的外角,那么请用文字描述(1)中的关系式;
(3)用你发现的结论解决下列问题:
如图3,AE,DE分别是四边形ABCD的外角∠NAD,∠MDA的平分线,∠B+∠C=240°,求∠E的度数.
图1
图2
图3
解:(1)∵∠3,∠4,∠5,∠6是四边形的四个内角,
∴∠3+∠4+∠5+∠6=360°.
∴∠3+∠4=360°-(∠5+∠6).
∵∠1+∠5=180°,∠2+∠6=180°,
∴∠1+∠2=360°-(∠5+∠6).
∴∠1+∠2=∠3+∠4.
(2)四边形的任意两个外角的和等于与它们不相邻的两个内角的和.
(3)∵∠B+∠C=240°,
∴∠MDA+∠NAD=240°.
∵AE,DE分别是∠NAD,∠MDA的平分线,
∴∠ADE=∠MDA,∠DAE=∠NAD.
∴∠ADE+∠DAE=(∠MDA+∠NAD)=120°.
∴∠E=180°-(∠ADE+∠DAE)=60°.
同步练习题
2021-2022学年人教版八年级数学上册
A组(基础题)
1.如图,从多边形的一个顶点出发作它的对角线,结合图形完成下表:
多边形的边数
4
5
6
…
n
分成三角形的个数
…
多边形的内角和
…
2.已知一个多边形的内角和是1
080°,则这个多边形是(
)
A.五边形
B.六边形
C.七边形
D.八边形
3.如图,该硬币边缘镌刻的正九边形的每个内角的度数是_________.
4.求如图所示的图形中x的值:
5.(1)正十边形的外角和为______;
(2)已知正多边形的一个外角为36°,则该正多边形的边数为______.
6.如图,五边形ABCDE的外角中,∠1=∠2=∠3=∠4=75°,则∠A的度数是______.
7.一个多边形的内角和是外角和的2倍,这个多边形是几边形?
8.如果一个多边形的每个外角都相等,且比内角小36°,求这个多边形的边数和内角和.
9.把一个多边形割去一个角后,得到的多边形的内角和为1440°,则原多边形的边数为______.
B组(中档题)
10.如图,小明从点A出发沿直线前进10米到达点B,向左转45°后又沿直线前进10米到达点C,再向左转45°后沿直线前进10米到达点D,……,照这样走下去,小明第一次回到出发点A时所走的路程为(
)
A.100米
B.80米
C.60米
D.40米
11.将一个n边形变成(n+1)边形,内角和将(
)
A.减少180°
B.增加90°
C.增加180°
D.增加360°
12.如图,在五边形ABCDE中,若去掉一个30°的角后得到一个六边形BCDEMN,则∠1+∠2的度数为(
)
A.210°
B.110°
C.150°
D.100°
13.如图,∠A+∠B+∠C+∠D+∠E+∠F=______.
14.如图,在正六边形ABCDEF中,连接AD,∠ADC=60°.求证:BC∥AD∥EF.
15.若一个多边形除了一个内角外,其余内角的和为2
680°,则这个内角是多少度?
C组(综合题)
16.(1)如图1,2,试探究其中∠1,∠2与∠3,∠4之间的数量关系;
(2)如果把∠1,∠2称为四边形的外角,那么请用文字描述(1)中的关系式;
(3)用你发现的结论解决下列问题:
如图3,AE,DE分别是四边形ABCD的外角∠NAD,∠MDA的平分线,∠B+∠C=240°,求∠E的度数.
图1
图2
图3
参考答案
11.3.2多边形的内角和同步练习题2021-2022学年人教版八年级数学上册
A组(基础题)
1.如图,从多边形的一个顶点出发作它的对角线,结合图形完成下表:
多边形的边数
4
5
6
…
n
分成三角形的个数
2
3
4
…
n-2
多边形的内角和
360°
540°
720°
…
(n-2)×180°
2.已知一个多边形的内角和是1
080°,则这个多边形是(D)
A.五边形
B.六边形
C.七边形
D.八边形
3.如图,该硬币边缘镌刻的正九边形的每个内角的度数是140°.
4.求如图所示的图形中x的值:
解:(1)根据图形可知:x=360-150-90-70=50.
(2)根据图形可知:x=180-[360-(90+73+82)]=65.
(3)根据图形可知:x+x+30+60+x+x-10=(5-2)×180.解得x=115.
5.(1)正十边形的外角和为360°;
(2)已知正多边形的一个外角为36°,则该正多边形的边数为10.
6.如图,五边形ABCDE的外角中,∠1=∠2=∠3=∠4=75°,则∠A的度数是120°.
7.一个多边形的内角和是外角和的2倍,这个多边形是几边形?
解:设这个多边形的边数为n,由题意,得
(n-2)·180°=360°×2.
解得n=6.
答:这个多边形是六边形.
8.如果一个多边形的每个外角都相等,且比内角小36°,求这个多边形的边数和内角和.
解:设多边形的一个外角为x°,则一个内角为(x+36)°,依题意,得
x+x+36=180,
解得x=72.
360°÷72°=5,
(5-2)×180°=540°.
故这个多边形的边数为5,内角和是540°.
9.把一个多边形割去一个角后,得到的多边形的内角和为1
440°,则原多边形的边数为9或10或11.
B组(中档题)
10.如图,小明从点A出发沿直线前进10米到达点B,向左转45°后又沿直线前进10米到达点C,再向左转45°后沿直线前进10米到达点D,……,照这样走下去,小明第一次回到出发点A时所走的路程为(B)
A.100米
B.80米
C.60米
D.40米
11.将一个n边形变成(n+1)边形,内角和将(C)
A.减少180°
B.增加90°
C.增加180°
D.增加360°
12.如图,在五边形ABCDE中,若去掉一个30°的角后得到一个六边形BCDEMN,则∠1+∠2的度数为(A)
A.210°
B.110°
C.150°
D.100°
13.如图,∠A+∠B+∠C+∠D+∠E+∠F=360°.
14.如图,在正六边形ABCDEF中,连接AD,∠ADC=60°.求证:BC∥AD∥EF.
证明:正六边形的每个内角的度数为=120°,
∵∠ADC=60°,∠CDE=120°,
∴∠ADE=60°.
又∵∠C=∠E=120°,
∴∠C+∠ADC=180°,∠E+∠ADE=180°.
∴BC∥AD,AD∥EF.
∴BC∥AD∥EF.
15.若一个多边形除了一个内角外,其余内角的和为2
680°,则这个内角是多少度?
解:设这个内角度数为x°,边数为n,
则(n-2)×180-x=2
680,
∴n=.
∵n为正整数,0<x<180,
∴n=17.
∴这个内角度数为180°×(17-2)-2
680°=20°.
故这个内角的度数是20°.
C组(综合题)
16.(1)如图1,2,试探究其中∠1,∠2与∠3,∠4之间的数量关系;
(2)如果把∠1,∠2称为四边形的外角,那么请用文字描述(1)中的关系式;
(3)用你发现的结论解决下列问题:
如图3,AE,DE分别是四边形ABCD的外角∠NAD,∠MDA的平分线,∠B+∠C=240°,求∠E的度数.
图1
图2
图3
解:(1)∵∠3,∠4,∠5,∠6是四边形的四个内角,
∴∠3+∠4+∠5+∠6=360°.
∴∠3+∠4=360°-(∠5+∠6).
∵∠1+∠5=180°,∠2+∠6=180°,
∴∠1+∠2=360°-(∠5+∠6).
∴∠1+∠2=∠3+∠4.
(2)四边形的任意两个外角的和等于与它们不相邻的两个内角的和.
(3)∵∠B+∠C=240°,
∴∠MDA+∠NAD=240°.
∵AE,DE分别是∠NAD,∠MDA的平分线,
∴∠ADE=∠MDA,∠DAE=∠NAD.
∴∠ADE+∠DAE=(∠MDA+∠NAD)=120°.
∴∠E=180°-(∠ADE+∠DAE)=60°.
