2020-2021学年黑龙江省绥化市海伦市七年级(下)期末数学试卷(五四学制)(Word版含解析)
文档属性
| 名称 | 2020-2021学年黑龙江省绥化市海伦市七年级(下)期末数学试卷(五四学制)(Word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 698.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-08-23 00:00:00 | ||
图片预览




文档简介
2020-2021学年黑龙江省绥化市海伦市七年级(下)期末数学试卷(五四学制)
一、选择题(共10小题,每题3分,共30分).
1.在0.25,,,,,中,无理数有( )
A.1个
B.2个
C.3个
D.4个
2.下面四个图形中,∠1=∠2一定成立的是( )
A.
B.
C.
D.
3.以下说法正确的是( )
A.同旁内角互补
B.有公共顶点、并且相等的两个角是对顶角
C.经过直线外一点,有且只有一条直线与这条直线平行
D.如果两个角之和等于180°,那么这两个角是为邻补角
4.下列调查中,最适合采用全面调查(普查)方式的是( )
A.对重庆市初中学生每天阅读时间的调查
B.对端午节期间市场上粽子质量情况的调查
C.对某批次手机的防水功能的调查
D.对某校九年级3班学生肺活量情况的调查
5.下列四组数中,是方程4x﹣y=10的解的是( )
A.
B.
C.
D.
6.如图,长方形内有两个相邻的正方形,面积分别为4和9,那么图中阴影部分的面积为( )
A.1
B.2
C.3
D.4
7.如图,下列不能判定AB∥CD的条件是( )
A.∠B+∠BCD=180°
B.∠1=∠2
C.∠3=∠4
D.∠B=∠5
8.已知a<b,则下列不等式一定成立的是( )
A.a+5>b+5
B.﹣2a<﹣2b
C.
D.4a﹣4b<0
9.某校运动员分组训练,若每组7人,余3人;若每组8人,则缺5人;设运动员人数为x人,组数为y组,则列方程组为( )
A.
B.
C.
D.
10.不等式2(x+1)<3x的解集在数轴上表示出来应为( )
A.
B.
C.
D.
二、填空题(共10小题,每题3分,共30分).
)
11.剧院里5排2号可用(5,2)表示,则(7,4)表示
.
12.﹣的相反数是
;|1﹣|=
.
13.如图,请你添加一个条件使得AD∥BC,所添的条件是
.
14.某中学要了解初二学生的视力情况,在全校初二年级中抽取了25名学生进行检测,在这个问题中,总体是
,样本是
.
15.已知在平面直角坐标系中,点P在第二象限,且到x轴的距离为3,到y轴的距离为4,则点P的坐标为
.
16.在以下现象中:①用打气筒打气时,气筒里活塞的运动;②传送帯上,瓶装饮料的移动;③在笔直的公路上行驶的汽车;④随风摆动的旗帜;⑤钟摆的摆动,属于平移现象的有
(只填序号).
17.已知a、b为两个连续整数,且,则a+b的值为
.
18.如果|x+1|+(y﹣5)2=0,那么x+y=
.
19.若方程组中未知数x,y满足x+y>0,则m的取值范围是
.
20.如图,已知A1(1,0),A2(1,1),A3(﹣1,1),A4(﹣1,﹣1),A5(2,﹣1)…,则A2021的坐标是
.
三、解答题(共60分)
21.(1)计算:|﹣3|﹣(﹣1)3+﹣;
(2)解方程组:.
22.解不等式组:,并求出最大整数解.
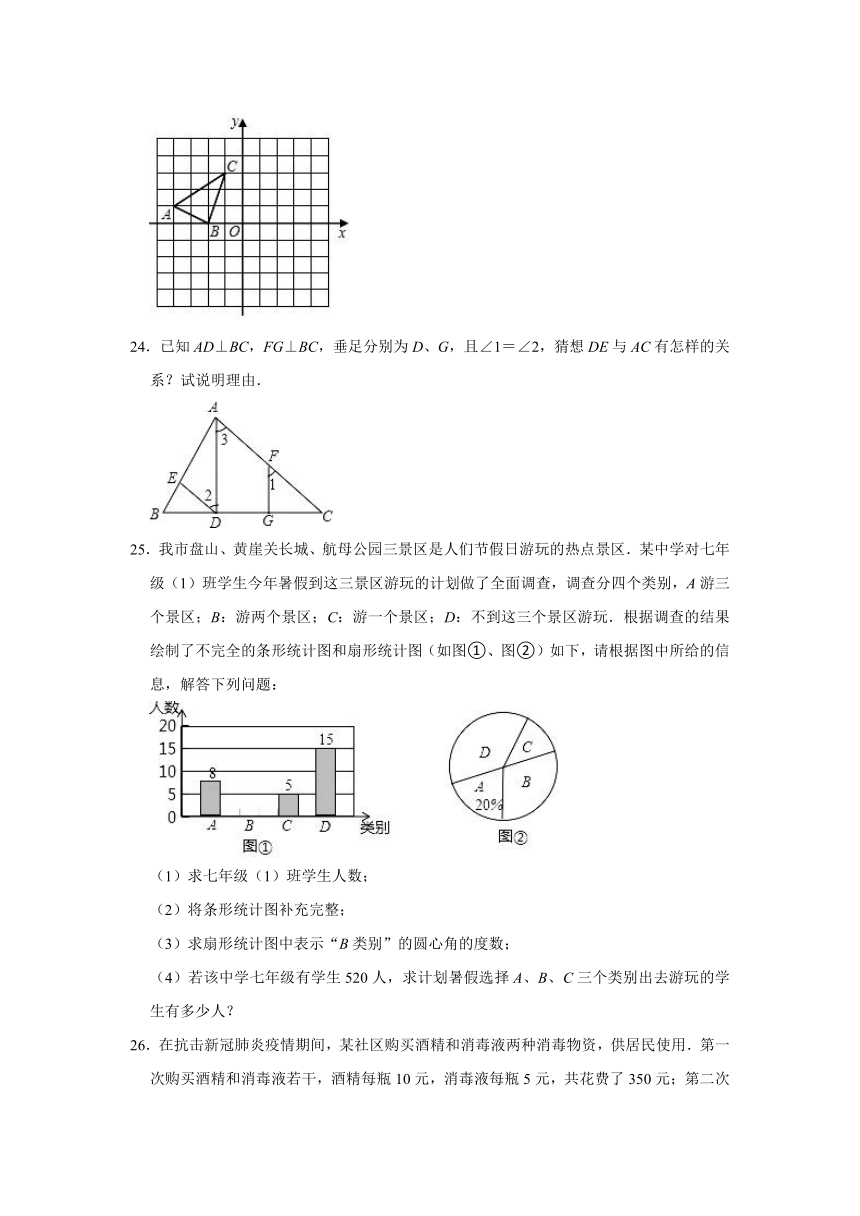
23.如图,将△ABC中向右平移4个单位得到△A'B'C'.
①写出A、B、C的坐标;
②画出△A'B'C';
③求△ABC的面积.
24.已知AD⊥BC,FG⊥BC,垂足分别为D、G,且∠1=∠2,猜想DE与AC有怎样的关系?试说明理由.
25.我市盘山、黄崖关长城、航母公园三景区是人们节假日游玩的热点景区.某中学对七年级(1)班学生今年暑假到这三景区游玩的计划做了全面调查,调查分四个类别,A游三个景区;B:游两个景区;C:游一个景区;D:不到这三个景区游玩.根据调查的结果绘制了不完全的条形统计图和扇形统计图(如图①、图②)如下,请根据图中所给的信息,解答下列问题:
(1)求七年级(1)班学生人数;
(2)将条形统计图补充完整;
(3)求扇形统计图中表示“B类别”的圆心角的度数;
(4)若该中学七年级有学生520人,求计划暑假选择A、B、C三个类别出去游玩的学生有多少人?
26.在抗击新冠肺炎疫情期间,某社区购买酒精和消毒液两种消毒物资,供居民使用.第一次购买酒精和消毒液若干,酒精每瓶10元,消毒液每瓶5元,共花费了350元;第二次又购买了与第一次相同数量的酒精和消毒液,由于酒精和消毒液每瓶价格分别下降了30%和20%,只花费了260元.求每次购买的酒精和消毒液分别是多少瓶?
27.某公司有A、B两种型号的客车共15辆,它们的载客量,每天的租金和车辆数如下表所示,已知在15辆客车都坐满的情况下,共载客570人
A型号客车
B型号客车
载客量(人/辆)
45
30
租金(元/辆)
400
280
车辆数(辆)
a
b
(1)求表中a,b的值;
(2)某中学计划租用A、B两种型号的客车共5辆,同时送七年级师生到基地参加社会实践活动,已知该中学租车的总费用不超过1900元.
①求最多能租用多少辆A型号客车?
②若七年级的师生共有195人,请写出所有可能的租车方案,并确定最省钱的租车方案.
参考答案
一、选择题(共10小题,每题3分,共30分).
1.在0.25,,,,,中,无理数有( )
A.1个
B.2个
C.3个
D.4个
【分析】无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.
解:0.25是有限小数,属于有理数;
,是分数,属于有理数;
无理数有,,,共3个.
故选:C.
2.下面四个图形中,∠1=∠2一定成立的是( )
A.
B.
C.
D.
【分析】根据对顶角、邻补角、平行线的性质及三角形的外角性质,可判断;
解:A、∠1、∠2是邻补角,∠1+∠2=180°;故本选项错误;
B、∠1、∠2是对顶角,根据其定义;故本选项正确;
C、根据平行线的性质:同位角相等,同旁内角互补,内错角相等;故本选项错误;
D、根据三角形的外角一定大于与它不相邻的内角;故本选项错误.
故选:B.
3.以下说法正确的是( )
A.同旁内角互补
B.有公共顶点、并且相等的两个角是对顶角
C.经过直线外一点,有且只有一条直线与这条直线平行
D.如果两个角之和等于180°,那么这两个角是为邻补角
【分析】利用相关的定义和性质对每个选项进行逐一判断即可.A,利用平行线的性质说明只有在特殊情形下才成立;B,利用对顶角的定义进行判定即可;C,利用平行线的性质判定即可;D,举出一个反例使它不成立即可.
解:∵两直线平行,同旁内角互补,
∴A选项错误;
∵一条角的平分线将这个角分成两个相等的角,但这两个相等的角不是对顶角,
∴B选项错误;
∵经过直线外一点,有且只有一条直线与这条直线平行,
∴C选项正确;
∵两直线平行,同旁内角互补,
∴D选项错误;
综上,正确的选项为:C.
故选:C.
4.下列调查中,最适合采用全面调查(普查)方式的是( )
A.对重庆市初中学生每天阅读时间的调查
B.对端午节期间市场上粽子质量情况的调查
C.对某批次手机的防水功能的调查
D.对某校九年级3班学生肺活量情况的调查
【分析】由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.
解:A、对重庆市初中学生每天阅读时间的调查,调查范围广适合抽样调查,故A错误;
B、对端午节期间市场上粽子质量情况的调查,调查具有破坏性,适合抽样调查,故B错误;
C、对某批次手机的防水功能的调查,调查具有破坏性,适合抽样调查,故C错误;
D、对某校九年级3班学生肺活量情况的调查,人数较少,适合普查,故D正确;
故选:D.
5.下列四组数中,是方程4x﹣y=10的解的是( )
A.
B.
C.
D.
【分析】将各选项代入即可得结果.
解:将A选项代入得4×1﹣6=﹣2,所以此选项不合题意;
将B选项代入得4×3.5﹣(﹣4)=18,所以此选项不合题意;
将C选项代入得4×15﹣4=56,所以此选项不合题意;
将D选项代入得4×0﹣(﹣10)=10,所以此选项符合题意,
故选:D.
6.如图,长方形内有两个相邻的正方形,面积分别为4和9,那么图中阴影部分的面积为( )
A.1
B.2
C.3
D.4
【分析】设两个正方形的边长是x、y(x<y),得出方程x2=4,y2=9,求出x=2,y=3,代入阴影部分的面积是(y﹣x)x求出即可.
解:设两个正方形的边长是x、y(x<y),
则x2=4,y2=9,
x=2,y=3,
则阴影部分的面积是(y﹣x)x=(3﹣2)×2=2,
故选:B.
7.如图,下列不能判定AB∥CD的条件是( )
A.∠B+∠BCD=180°
B.∠1=∠2
C.∠3=∠4
D.∠B=∠5
【分析】根据平行线的判定定理对各选项进行逐一判断即可.
解:A、∵∠B+∠BCD=180°,∴AB∥CD,故不符合题意;
B、∵∠1=∠2,∴AD∥BC,故符合题意;
C、∵∠3=∠4,∴AB∥CD,故不符合题意;
D、∵∠B=∠5,∴AB∥CD,故不符合题意.
故选:B.
8.已知a<b,则下列不等式一定成立的是( )
A.a+5>b+5
B.﹣2a<﹣2b
C.
D.4a﹣4b<0
【分析】根据不等式的性质,依次分析各个选项,选出不等式的变形不正确的选项即可.
解:A.若a<b,不等式两边同时加上5得:a+5<b+5,即A项不符合题意,
B.若a<b,不等式两边同时乘以﹣2得:﹣2a>﹣2b,即B项不符合题意,
C.若a<b,不等式两边同时乘以得:b,即C项不符合题意,
D.若a<b,不等式两边同时乘以4得:4a<4b,再两边同时减4b得,4a﹣4b<0,即D项符合题意,
故选:D.
9.某校运动员分组训练,若每组7人,余3人;若每组8人,则缺5人;设运动员人数为x人,组数为y组,则列方程组为( )
A.
B.
C.
D.
【分析】根据题意中的两种分法,分别找到等量关系:
①组数×每组7人=总人数﹣3人;②组数×每组8人=总人数+5人.
解:根据组数×每组7人=总人数﹣3人,得方程7y=x﹣3;根据组数×每组8人=总人数+5人,得方程8y=x+5.
列方程组为.
故选:C.
10.不等式2(x+1)<3x的解集在数轴上表示出来应为( )
A.
B.
C.
D.
【分析】首先解不等式,把不等式的解集表示出来,再对照答案的表示法判定则可.
解:去括号得:2x+2<3x
移项,合并同类项得:﹣x<﹣2即x>2.
故选:D.
二、填空题(共10小题,每题3分,共30分).
)
11.剧院里5排2号可用(5,2)表示,则(7,4)表示 7排4号 .
【分析】根据有序数对的第一个数表示排数,第二个数表示号数解答.
解:∵5排2号可以用(5,2)表示,
∴(7,4)表示7排4号.
故答案为:7排4号.
12.﹣的相反数是
﹣ ;|1﹣|= ﹣1 .
【分析】直接利用相反数的定义以及绝对值的性质分别得出答案.
解:﹣的相反数是:﹣(﹣)=﹣;
|1﹣|=﹣1.
故答案为:﹣;﹣1.
13.如图,请你添加一个条件使得AD∥BC,所添的条件是
∠EAD=∠B或∠CAD=∠C或∠BAD+∠B=180° .
【分析】根据平行线的判定方法进行添加.
解:根据同位角相等,两条直线平行,可以添加∠EAD=∠B;
根据内错角相等,两条直线平行,可以添加∠CAD=∠C;
根据同旁内角互补,两条直线平行,可以添加∠BAD+∠B=180°,
故答案为:∠EAD=∠B或∠CAD=∠C或∠BAD+∠B=180°.
14.某中学要了解初二学生的视力情况,在全校初二年级中抽取了25名学生进行检测,在这个问题中,总体是 某中学初二学生的视力情况的全体 ,样本是 25名学生的视力情况 .
【分析】总体是指考查的对象的全体,样本是总体中所抽取的一部分个体.我们在区分总体、样本这两个概念时,首先找出考查的对象.从而找出总体.再根据被收集数据的这一部分对象找出样本.
解:本题考察的对象是某中学初二学生的视力情况,故总体是某中学初二学生的视力情况的全体,样本是25名学生的视力情况.
15.已知在平面直角坐标系中,点P在第二象限,且到x轴的距离为3,到y轴的距离为4,则点P的坐标为 (﹣4,3) .
【分析】根据第二象限点的横坐标是负数,纵坐标是正数,点到x轴的距离等于纵坐标的长度,到y轴的距离等于横坐标的长度解答.
解:∵点P在第二象限,且到x轴的距离为3,到y轴的距离为4,
∴点P的横坐标为﹣4,纵坐标为3,
∴点P的坐标为(﹣4,3).
故答案为:(﹣4,3).
16.在以下现象中:①用打气筒打气时,气筒里活塞的运动;②传送帯上,瓶装饮料的移动;③在笔直的公路上行驶的汽车;④随风摆动的旗帜;⑤钟摆的摆动,属于平移现象的有
①②③ (只填序号).
【分析】根据平移的性质,做出判断,即图形平移前后的形状和大小没有变化,只是位置发生变化;图形平移后,对应点连成的线段平行且相等(或在同一直线上).
解:①用打气筒打气时,气筒里活塞的运动符合平移的定义,故正确;
②直线传送带上,瓶装饮料的移动符合平移的定义,故正确;
③在平直的公路上行驶的汽车符合平移的定义,故正确;
④随风摆动的旗帜不在同一条直线上,故错误;
⑤钟表的摆动不在同一条直线上,故错误;
故答案为:①②③.
17.已知a、b为两个连续整数,且,则a+b的值为 7 .
【分析】先估算出的大小,进而可得出a、b的值,进行计算即可.
解:∵<<,
∴a=3,b=4,
∴a+b=3+4=7.
故答案为:7.
18.如果|x+1|+(y﹣5)2=0,那么x+y= 4 .
【分析】根据绝对值和偶次方的非负性求出x、y的值,再代入计算即可.
解:∵|x+1|+(y﹣5)2=0,
∴x+1=0,y﹣5=0,
即x=﹣1,y=5,
∴x+y=﹣1+5=4,
故答案为:4.
19.若方程组中未知数x,y满足x+y>0,则m的取值范围是 m>﹣4 .
【分析】根据x、y的系数的特点,把两个方程相加用m表示出x+y,然后列出不等式求解即可.
解:,
①+②得,3(x+y)=m+4,
解得x+y=,
∵x+y>0,
∴>0,
解得m>﹣4.
故答案为:m>﹣4.
20.如图,已知A1(1,0),A2(1,1),A3(﹣1,1),A4(﹣1,﹣1),A5(2,﹣1)…,则A2021的坐标是 (506,﹣505). .
【分析】观察下标可知点A2021在第四象限,由此探究规律即可解决问题;
解:∵(2021﹣1)÷4=505,
∴点A2021在第四象限,纵坐标为﹣505,横坐标为505+1=506,
∴A2021的坐标是(506,﹣505).
故答案为(506,﹣505).
三、解答题(共60分)
21.(1)计算:|﹣3|﹣(﹣1)3+﹣;
(2)解方程组:.
【分析】(1)原式利用绝对值的代数意义,乘方的意义,算术平方根、立方根性质计算即可求出值;
(2)方程组利用加减消元法求出解即可.
解:(1)原式=3﹣(﹣1)﹣3﹣2
=3+1﹣3﹣2
=﹣1;
(2),
①+②×5得:27x=108,
解得:x=4,
把x=4代入①得:8+5y=23,
解得:y=3,
则方程组的解为.
22.解不等式组:,并求出最大整数解.
【分析】先求出不等式的解集,再求出不等式组的解集,即可得出答案.
解:,
由①得:x>1,
由②得:x≤6,
所以不等式解集为:1<x≤6,
最大整数解为:6.
23.如图,将△ABC中向右平移4个单位得到△A'B'C'.
①写出A、B、C的坐标;
②画出△A'B'C';
③求△ABC的面积.
【分析】①利用图中点的位置写出三个点的坐标;
②利用点平移的坐标特征写出点A′、B′、C′的坐标,然后描点即可;
③用一个矩形的面积分别减去三个直角三角形的面积去计算△ABC的面积.
解:①A(﹣4,1),B(﹣2,0),C(﹣1,3);
②如图,△A'B'C'为所作;
③△ABC的面积=3×3﹣×1×2﹣×3×1﹣×2×3=3.5.
24.已知AD⊥BC,FG⊥BC,垂足分别为D、G,且∠1=∠2,猜想DE与AC有怎样的关系?试说明理由.
【分析】根据平行线的判定定理、等量代换、平行线的性质定理证明.
解:ED∥AC,
理由如下:∵AD⊥BC,FG⊥BC,
∴∠ADC=∠FGC=90°,
∴AD∥FG,
∴∠1=∠3,
∵∠1=∠2,
∴∠3=∠2,
∴ED∥AC.
25.我市盘山、黄崖关长城、航母公园三景区是人们节假日游玩的热点景区.某中学对七年级(1)班学生今年暑假到这三景区游玩的计划做了全面调查,调查分四个类别,A游三个景区;B:游两个景区;C:游一个景区;D:不到这三个景区游玩.根据调查的结果绘制了不完全的条形统计图和扇形统计图(如图①、图②)如下,请根据图中所给的信息,解答下列问题:
(1)求七年级(1)班学生人数;
(2)将条形统计图补充完整;
(3)求扇形统计图中表示“B类别”的圆心角的度数;
(4)若该中学七年级有学生520人,求计划暑假选择A、B、C三个类别出去游玩的学生有多少人?
【分析】(1)根据统计图中的数据可以求得七年级(1)班的学生人数;
(2)根据(1)中的结果和统计图中的数据可以求得选择B的人数,从而可以将条形统计图补充完整;
(3)根据统计图中的数据可以求得扇形统计图中表示“B类别”的圆心角的度数;
(4)根据统计图中的数据可以求得计划暑假选择A、B、C三个类别出去游玩的学生有多少人.
解:(1)8÷20%=40(人),
即七年级(1)班有学生40人;
(2)选择B的学生有:40﹣8﹣5﹣15=12(人),
补全的条形统计图如右图所示;
(3)扇形统计图中表示“B类别”的圆心角的度数是:360°×=108°;
(4)520×=325(人),
答:计划暑假选择A、B、C三个类别出去游玩的学生有325人.
26.在抗击新冠肺炎疫情期间,某社区购买酒精和消毒液两种消毒物资,供居民使用.第一次购买酒精和消毒液若干,酒精每瓶10元,消毒液每瓶5元,共花费了350元;第二次又购买了与第一次相同数量的酒精和消毒液,由于酒精和消毒液每瓶价格分别下降了30%和20%,只花费了260元.求每次购买的酒精和消毒液分别是多少瓶?
【分析】设每次购买酒精x瓶,消毒液y瓶,根据总价=单价×数量,结合两次购买所需费用,即可得出关于x,y的二元一次方程组,解之即可得出结论.
解:设每次购买酒精x瓶,消毒液y瓶,
依题意得:,
解得:.
答:每次购买酒精20瓶,消毒液30瓶.
27.某公司有A、B两种型号的客车共15辆,它们的载客量,每天的租金和车辆数如下表所示,已知在15辆客车都坐满的情况下,共载客570人
A型号客车
B型号客车
载客量(人/辆)
45
30
租金(元/辆)
400
280
车辆数(辆)
a
b
(1)求表中a,b的值;
(2)某中学计划租用A、B两种型号的客车共5辆,同时送七年级师生到基地参加社会实践活动,已知该中学租车的总费用不超过1900元.
①求最多能租用多少辆A型号客车?
②若七年级的师生共有195人,请写出所有可能的租车方案,并确定最省钱的租车方案.
【分析】(1)利用客车的总数为15和在15辆客车都坐满的情况下,共载客570人可列方程组,然后解方程即可得到a和b的值;
(2)①设计划租用A种型号的客车x辆,则计划租用B种型号的客车(5﹣x)辆,利用该中学租车的总费用不超过1900元可列不等式400x+280(5﹣x)≤1900,然后解不等式,利用x为正整数,求出此解集中最大的正整数即可;
②利用两种客车的人数不少于195列不等式得到+30(5﹣x)≥195,解得x≥3,加上x≤4,于是得到x=3,4,然后写出两个方案,通过计算两方案的费用得到最省钱的租车方案
解:(1)由题意得,解得;
(2)①设计划租用A种型号的客车x辆,则计划租用B种型号的客车(5﹣x)辆,
根据题意得400x+280(5﹣x)≤1900,解得x≤4,
因为x取非负整数,
所以x的最大值为4,
答:最多能租用4辆A型号客车;
②根据题意得45x+30(5﹣x)≥195,解得x≥3,
而x≤4,
所以3≤x≤4,
因为x为正整数,
所以x=3,4,
所有可能的租车方案为
方案一:租用A种型号的客车3辆,租用B种型号的客车2辆,此时费用为3×400+2×280=1760(元)
方案二:租用A种型号的客车4辆,租用B种型号的客车1辆;此时费用为4×400+1×280=1880(元)
所以最省钱的租车方案为租用A种型号的客车3辆,租用B种型号的客车2辆.
一、选择题(共10小题,每题3分,共30分).
1.在0.25,,,,,中,无理数有( )
A.1个
B.2个
C.3个
D.4个
2.下面四个图形中,∠1=∠2一定成立的是( )
A.
B.
C.
D.
3.以下说法正确的是( )
A.同旁内角互补
B.有公共顶点、并且相等的两个角是对顶角
C.经过直线外一点,有且只有一条直线与这条直线平行
D.如果两个角之和等于180°,那么这两个角是为邻补角
4.下列调查中,最适合采用全面调查(普查)方式的是( )
A.对重庆市初中学生每天阅读时间的调查
B.对端午节期间市场上粽子质量情况的调查
C.对某批次手机的防水功能的调查
D.对某校九年级3班学生肺活量情况的调查
5.下列四组数中,是方程4x﹣y=10的解的是( )
A.
B.
C.
D.
6.如图,长方形内有两个相邻的正方形,面积分别为4和9,那么图中阴影部分的面积为( )
A.1
B.2
C.3
D.4
7.如图,下列不能判定AB∥CD的条件是( )
A.∠B+∠BCD=180°
B.∠1=∠2
C.∠3=∠4
D.∠B=∠5
8.已知a<b,则下列不等式一定成立的是( )
A.a+5>b+5
B.﹣2a<﹣2b
C.
D.4a﹣4b<0
9.某校运动员分组训练,若每组7人,余3人;若每组8人,则缺5人;设运动员人数为x人,组数为y组,则列方程组为( )
A.
B.
C.
D.
10.不等式2(x+1)<3x的解集在数轴上表示出来应为( )
A.
B.
C.
D.
二、填空题(共10小题,每题3分,共30分).
)
11.剧院里5排2号可用(5,2)表示,则(7,4)表示
.
12.﹣的相反数是
;|1﹣|=
.
13.如图,请你添加一个条件使得AD∥BC,所添的条件是
.
14.某中学要了解初二学生的视力情况,在全校初二年级中抽取了25名学生进行检测,在这个问题中,总体是
,样本是
.
15.已知在平面直角坐标系中,点P在第二象限,且到x轴的距离为3,到y轴的距离为4,则点P的坐标为
.
16.在以下现象中:①用打气筒打气时,气筒里活塞的运动;②传送帯上,瓶装饮料的移动;③在笔直的公路上行驶的汽车;④随风摆动的旗帜;⑤钟摆的摆动,属于平移现象的有
(只填序号).
17.已知a、b为两个连续整数,且,则a+b的值为
.
18.如果|x+1|+(y﹣5)2=0,那么x+y=
.
19.若方程组中未知数x,y满足x+y>0,则m的取值范围是
.
20.如图,已知A1(1,0),A2(1,1),A3(﹣1,1),A4(﹣1,﹣1),A5(2,﹣1)…,则A2021的坐标是
.
三、解答题(共60分)
21.(1)计算:|﹣3|﹣(﹣1)3+﹣;
(2)解方程组:.
22.解不等式组:,并求出最大整数解.
23.如图,将△ABC中向右平移4个单位得到△A'B'C'.
①写出A、B、C的坐标;
②画出△A'B'C';
③求△ABC的面积.
24.已知AD⊥BC,FG⊥BC,垂足分别为D、G,且∠1=∠2,猜想DE与AC有怎样的关系?试说明理由.
25.我市盘山、黄崖关长城、航母公园三景区是人们节假日游玩的热点景区.某中学对七年级(1)班学生今年暑假到这三景区游玩的计划做了全面调查,调查分四个类别,A游三个景区;B:游两个景区;C:游一个景区;D:不到这三个景区游玩.根据调查的结果绘制了不完全的条形统计图和扇形统计图(如图①、图②)如下,请根据图中所给的信息,解答下列问题:
(1)求七年级(1)班学生人数;
(2)将条形统计图补充完整;
(3)求扇形统计图中表示“B类别”的圆心角的度数;
(4)若该中学七年级有学生520人,求计划暑假选择A、B、C三个类别出去游玩的学生有多少人?
26.在抗击新冠肺炎疫情期间,某社区购买酒精和消毒液两种消毒物资,供居民使用.第一次购买酒精和消毒液若干,酒精每瓶10元,消毒液每瓶5元,共花费了350元;第二次又购买了与第一次相同数量的酒精和消毒液,由于酒精和消毒液每瓶价格分别下降了30%和20%,只花费了260元.求每次购买的酒精和消毒液分别是多少瓶?
27.某公司有A、B两种型号的客车共15辆,它们的载客量,每天的租金和车辆数如下表所示,已知在15辆客车都坐满的情况下,共载客570人
A型号客车
B型号客车
载客量(人/辆)
45
30
租金(元/辆)
400
280
车辆数(辆)
a
b
(1)求表中a,b的值;
(2)某中学计划租用A、B两种型号的客车共5辆,同时送七年级师生到基地参加社会实践活动,已知该中学租车的总费用不超过1900元.
①求最多能租用多少辆A型号客车?
②若七年级的师生共有195人,请写出所有可能的租车方案,并确定最省钱的租车方案.
参考答案
一、选择题(共10小题,每题3分,共30分).
1.在0.25,,,,,中,无理数有( )
A.1个
B.2个
C.3个
D.4个
【分析】无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.
解:0.25是有限小数,属于有理数;
,是分数,属于有理数;
无理数有,,,共3个.
故选:C.
2.下面四个图形中,∠1=∠2一定成立的是( )
A.
B.
C.
D.
【分析】根据对顶角、邻补角、平行线的性质及三角形的外角性质,可判断;
解:A、∠1、∠2是邻补角,∠1+∠2=180°;故本选项错误;
B、∠1、∠2是对顶角,根据其定义;故本选项正确;
C、根据平行线的性质:同位角相等,同旁内角互补,内错角相等;故本选项错误;
D、根据三角形的外角一定大于与它不相邻的内角;故本选项错误.
故选:B.
3.以下说法正确的是( )
A.同旁内角互补
B.有公共顶点、并且相等的两个角是对顶角
C.经过直线外一点,有且只有一条直线与这条直线平行
D.如果两个角之和等于180°,那么这两个角是为邻补角
【分析】利用相关的定义和性质对每个选项进行逐一判断即可.A,利用平行线的性质说明只有在特殊情形下才成立;B,利用对顶角的定义进行判定即可;C,利用平行线的性质判定即可;D,举出一个反例使它不成立即可.
解:∵两直线平行,同旁内角互补,
∴A选项错误;
∵一条角的平分线将这个角分成两个相等的角,但这两个相等的角不是对顶角,
∴B选项错误;
∵经过直线外一点,有且只有一条直线与这条直线平行,
∴C选项正确;
∵两直线平行,同旁内角互补,
∴D选项错误;
综上,正确的选项为:C.
故选:C.
4.下列调查中,最适合采用全面调查(普查)方式的是( )
A.对重庆市初中学生每天阅读时间的调查
B.对端午节期间市场上粽子质量情况的调查
C.对某批次手机的防水功能的调查
D.对某校九年级3班学生肺活量情况的调查
【分析】由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.
解:A、对重庆市初中学生每天阅读时间的调查,调查范围广适合抽样调查,故A错误;
B、对端午节期间市场上粽子质量情况的调查,调查具有破坏性,适合抽样调查,故B错误;
C、对某批次手机的防水功能的调查,调查具有破坏性,适合抽样调查,故C错误;
D、对某校九年级3班学生肺活量情况的调查,人数较少,适合普查,故D正确;
故选:D.
5.下列四组数中,是方程4x﹣y=10的解的是( )
A.
B.
C.
D.
【分析】将各选项代入即可得结果.
解:将A选项代入得4×1﹣6=﹣2,所以此选项不合题意;
将B选项代入得4×3.5﹣(﹣4)=18,所以此选项不合题意;
将C选项代入得4×15﹣4=56,所以此选项不合题意;
将D选项代入得4×0﹣(﹣10)=10,所以此选项符合题意,
故选:D.
6.如图,长方形内有两个相邻的正方形,面积分别为4和9,那么图中阴影部分的面积为( )
A.1
B.2
C.3
D.4
【分析】设两个正方形的边长是x、y(x<y),得出方程x2=4,y2=9,求出x=2,y=3,代入阴影部分的面积是(y﹣x)x求出即可.
解:设两个正方形的边长是x、y(x<y),
则x2=4,y2=9,
x=2,y=3,
则阴影部分的面积是(y﹣x)x=(3﹣2)×2=2,
故选:B.
7.如图,下列不能判定AB∥CD的条件是( )
A.∠B+∠BCD=180°
B.∠1=∠2
C.∠3=∠4
D.∠B=∠5
【分析】根据平行线的判定定理对各选项进行逐一判断即可.
解:A、∵∠B+∠BCD=180°,∴AB∥CD,故不符合题意;
B、∵∠1=∠2,∴AD∥BC,故符合题意;
C、∵∠3=∠4,∴AB∥CD,故不符合题意;
D、∵∠B=∠5,∴AB∥CD,故不符合题意.
故选:B.
8.已知a<b,则下列不等式一定成立的是( )
A.a+5>b+5
B.﹣2a<﹣2b
C.
D.4a﹣4b<0
【分析】根据不等式的性质,依次分析各个选项,选出不等式的变形不正确的选项即可.
解:A.若a<b,不等式两边同时加上5得:a+5<b+5,即A项不符合题意,
B.若a<b,不等式两边同时乘以﹣2得:﹣2a>﹣2b,即B项不符合题意,
C.若a<b,不等式两边同时乘以得:b,即C项不符合题意,
D.若a<b,不等式两边同时乘以4得:4a<4b,再两边同时减4b得,4a﹣4b<0,即D项符合题意,
故选:D.
9.某校运动员分组训练,若每组7人,余3人;若每组8人,则缺5人;设运动员人数为x人,组数为y组,则列方程组为( )
A.
B.
C.
D.
【分析】根据题意中的两种分法,分别找到等量关系:
①组数×每组7人=总人数﹣3人;②组数×每组8人=总人数+5人.
解:根据组数×每组7人=总人数﹣3人,得方程7y=x﹣3;根据组数×每组8人=总人数+5人,得方程8y=x+5.
列方程组为.
故选:C.
10.不等式2(x+1)<3x的解集在数轴上表示出来应为( )
A.
B.
C.
D.
【分析】首先解不等式,把不等式的解集表示出来,再对照答案的表示法判定则可.
解:去括号得:2x+2<3x
移项,合并同类项得:﹣x<﹣2即x>2.
故选:D.
二、填空题(共10小题,每题3分,共30分).
)
11.剧院里5排2号可用(5,2)表示,则(7,4)表示 7排4号 .
【分析】根据有序数对的第一个数表示排数,第二个数表示号数解答.
解:∵5排2号可以用(5,2)表示,
∴(7,4)表示7排4号.
故答案为:7排4号.
12.﹣的相反数是
﹣ ;|1﹣|= ﹣1 .
【分析】直接利用相反数的定义以及绝对值的性质分别得出答案.
解:﹣的相反数是:﹣(﹣)=﹣;
|1﹣|=﹣1.
故答案为:﹣;﹣1.
13.如图,请你添加一个条件使得AD∥BC,所添的条件是
∠EAD=∠B或∠CAD=∠C或∠BAD+∠B=180° .
【分析】根据平行线的判定方法进行添加.
解:根据同位角相等,两条直线平行,可以添加∠EAD=∠B;
根据内错角相等,两条直线平行,可以添加∠CAD=∠C;
根据同旁内角互补,两条直线平行,可以添加∠BAD+∠B=180°,
故答案为:∠EAD=∠B或∠CAD=∠C或∠BAD+∠B=180°.
14.某中学要了解初二学生的视力情况,在全校初二年级中抽取了25名学生进行检测,在这个问题中,总体是 某中学初二学生的视力情况的全体 ,样本是 25名学生的视力情况 .
【分析】总体是指考查的对象的全体,样本是总体中所抽取的一部分个体.我们在区分总体、样本这两个概念时,首先找出考查的对象.从而找出总体.再根据被收集数据的这一部分对象找出样本.
解:本题考察的对象是某中学初二学生的视力情况,故总体是某中学初二学生的视力情况的全体,样本是25名学生的视力情况.
15.已知在平面直角坐标系中,点P在第二象限,且到x轴的距离为3,到y轴的距离为4,则点P的坐标为 (﹣4,3) .
【分析】根据第二象限点的横坐标是负数,纵坐标是正数,点到x轴的距离等于纵坐标的长度,到y轴的距离等于横坐标的长度解答.
解:∵点P在第二象限,且到x轴的距离为3,到y轴的距离为4,
∴点P的横坐标为﹣4,纵坐标为3,
∴点P的坐标为(﹣4,3).
故答案为:(﹣4,3).
16.在以下现象中:①用打气筒打气时,气筒里活塞的运动;②传送帯上,瓶装饮料的移动;③在笔直的公路上行驶的汽车;④随风摆动的旗帜;⑤钟摆的摆动,属于平移现象的有
①②③ (只填序号).
【分析】根据平移的性质,做出判断,即图形平移前后的形状和大小没有变化,只是位置发生变化;图形平移后,对应点连成的线段平行且相等(或在同一直线上).
解:①用打气筒打气时,气筒里活塞的运动符合平移的定义,故正确;
②直线传送带上,瓶装饮料的移动符合平移的定义,故正确;
③在平直的公路上行驶的汽车符合平移的定义,故正确;
④随风摆动的旗帜不在同一条直线上,故错误;
⑤钟表的摆动不在同一条直线上,故错误;
故答案为:①②③.
17.已知a、b为两个连续整数,且,则a+b的值为 7 .
【分析】先估算出的大小,进而可得出a、b的值,进行计算即可.
解:∵<<,
∴a=3,b=4,
∴a+b=3+4=7.
故答案为:7.
18.如果|x+1|+(y﹣5)2=0,那么x+y= 4 .
【分析】根据绝对值和偶次方的非负性求出x、y的值,再代入计算即可.
解:∵|x+1|+(y﹣5)2=0,
∴x+1=0,y﹣5=0,
即x=﹣1,y=5,
∴x+y=﹣1+5=4,
故答案为:4.
19.若方程组中未知数x,y满足x+y>0,则m的取值范围是 m>﹣4 .
【分析】根据x、y的系数的特点,把两个方程相加用m表示出x+y,然后列出不等式求解即可.
解:,
①+②得,3(x+y)=m+4,
解得x+y=,
∵x+y>0,
∴>0,
解得m>﹣4.
故答案为:m>﹣4.
20.如图,已知A1(1,0),A2(1,1),A3(﹣1,1),A4(﹣1,﹣1),A5(2,﹣1)…,则A2021的坐标是 (506,﹣505). .
【分析】观察下标可知点A2021在第四象限,由此探究规律即可解决问题;
解:∵(2021﹣1)÷4=505,
∴点A2021在第四象限,纵坐标为﹣505,横坐标为505+1=506,
∴A2021的坐标是(506,﹣505).
故答案为(506,﹣505).
三、解答题(共60分)
21.(1)计算:|﹣3|﹣(﹣1)3+﹣;
(2)解方程组:.
【分析】(1)原式利用绝对值的代数意义,乘方的意义,算术平方根、立方根性质计算即可求出值;
(2)方程组利用加减消元法求出解即可.
解:(1)原式=3﹣(﹣1)﹣3﹣2
=3+1﹣3﹣2
=﹣1;
(2),
①+②×5得:27x=108,
解得:x=4,
把x=4代入①得:8+5y=23,
解得:y=3,
则方程组的解为.
22.解不等式组:,并求出最大整数解.
【分析】先求出不等式的解集,再求出不等式组的解集,即可得出答案.
解:,
由①得:x>1,
由②得:x≤6,
所以不等式解集为:1<x≤6,
最大整数解为:6.
23.如图,将△ABC中向右平移4个单位得到△A'B'C'.
①写出A、B、C的坐标;
②画出△A'B'C';
③求△ABC的面积.
【分析】①利用图中点的位置写出三个点的坐标;
②利用点平移的坐标特征写出点A′、B′、C′的坐标,然后描点即可;
③用一个矩形的面积分别减去三个直角三角形的面积去计算△ABC的面积.
解:①A(﹣4,1),B(﹣2,0),C(﹣1,3);
②如图,△A'B'C'为所作;
③△ABC的面积=3×3﹣×1×2﹣×3×1﹣×2×3=3.5.
24.已知AD⊥BC,FG⊥BC,垂足分别为D、G,且∠1=∠2,猜想DE与AC有怎样的关系?试说明理由.
【分析】根据平行线的判定定理、等量代换、平行线的性质定理证明.
解:ED∥AC,
理由如下:∵AD⊥BC,FG⊥BC,
∴∠ADC=∠FGC=90°,
∴AD∥FG,
∴∠1=∠3,
∵∠1=∠2,
∴∠3=∠2,
∴ED∥AC.
25.我市盘山、黄崖关长城、航母公园三景区是人们节假日游玩的热点景区.某中学对七年级(1)班学生今年暑假到这三景区游玩的计划做了全面调查,调查分四个类别,A游三个景区;B:游两个景区;C:游一个景区;D:不到这三个景区游玩.根据调查的结果绘制了不完全的条形统计图和扇形统计图(如图①、图②)如下,请根据图中所给的信息,解答下列问题:
(1)求七年级(1)班学生人数;
(2)将条形统计图补充完整;
(3)求扇形统计图中表示“B类别”的圆心角的度数;
(4)若该中学七年级有学生520人,求计划暑假选择A、B、C三个类别出去游玩的学生有多少人?
【分析】(1)根据统计图中的数据可以求得七年级(1)班的学生人数;
(2)根据(1)中的结果和统计图中的数据可以求得选择B的人数,从而可以将条形统计图补充完整;
(3)根据统计图中的数据可以求得扇形统计图中表示“B类别”的圆心角的度数;
(4)根据统计图中的数据可以求得计划暑假选择A、B、C三个类别出去游玩的学生有多少人.
解:(1)8÷20%=40(人),
即七年级(1)班有学生40人;
(2)选择B的学生有:40﹣8﹣5﹣15=12(人),
补全的条形统计图如右图所示;
(3)扇形统计图中表示“B类别”的圆心角的度数是:360°×=108°;
(4)520×=325(人),
答:计划暑假选择A、B、C三个类别出去游玩的学生有325人.
26.在抗击新冠肺炎疫情期间,某社区购买酒精和消毒液两种消毒物资,供居民使用.第一次购买酒精和消毒液若干,酒精每瓶10元,消毒液每瓶5元,共花费了350元;第二次又购买了与第一次相同数量的酒精和消毒液,由于酒精和消毒液每瓶价格分别下降了30%和20%,只花费了260元.求每次购买的酒精和消毒液分别是多少瓶?
【分析】设每次购买酒精x瓶,消毒液y瓶,根据总价=单价×数量,结合两次购买所需费用,即可得出关于x,y的二元一次方程组,解之即可得出结论.
解:设每次购买酒精x瓶,消毒液y瓶,
依题意得:,
解得:.
答:每次购买酒精20瓶,消毒液30瓶.
27.某公司有A、B两种型号的客车共15辆,它们的载客量,每天的租金和车辆数如下表所示,已知在15辆客车都坐满的情况下,共载客570人
A型号客车
B型号客车
载客量(人/辆)
45
30
租金(元/辆)
400
280
车辆数(辆)
a
b
(1)求表中a,b的值;
(2)某中学计划租用A、B两种型号的客车共5辆,同时送七年级师生到基地参加社会实践活动,已知该中学租车的总费用不超过1900元.
①求最多能租用多少辆A型号客车?
②若七年级的师生共有195人,请写出所有可能的租车方案,并确定最省钱的租车方案.
【分析】(1)利用客车的总数为15和在15辆客车都坐满的情况下,共载客570人可列方程组,然后解方程即可得到a和b的值;
(2)①设计划租用A种型号的客车x辆,则计划租用B种型号的客车(5﹣x)辆,利用该中学租车的总费用不超过1900元可列不等式400x+280(5﹣x)≤1900,然后解不等式,利用x为正整数,求出此解集中最大的正整数即可;
②利用两种客车的人数不少于195列不等式得到+30(5﹣x)≥195,解得x≥3,加上x≤4,于是得到x=3,4,然后写出两个方案,通过计算两方案的费用得到最省钱的租车方案
解:(1)由题意得,解得;
(2)①设计划租用A种型号的客车x辆,则计划租用B种型号的客车(5﹣x)辆,
根据题意得400x+280(5﹣x)≤1900,解得x≤4,
因为x取非负整数,
所以x的最大值为4,
答:最多能租用4辆A型号客车;
②根据题意得45x+30(5﹣x)≥195,解得x≥3,
而x≤4,
所以3≤x≤4,
因为x为正整数,
所以x=3,4,
所有可能的租车方案为
方案一:租用A种型号的客车3辆,租用B种型号的客车2辆,此时费用为3×400+2×280=1760(元)
方案二:租用A种型号的客车4辆,租用B种型号的客车1辆;此时费用为4×400+1×280=1880(元)
所以最省钱的租车方案为租用A种型号的客车3辆,租用B种型号的客车2辆.
同课章节目录
